GNN 综述
一、Deep Learning On Graph[2018]
将传统深度学习框架应用于图数据存在一些挑战:
- 图的不规则结构:和网格结构的图像、音频、文本数据不同,图数据具有不规则的结构,因此很难将一些基础的数学算子推广到图上。如,为图数据定义卷积、池化算法并不简单。这个问题通常被称作几何深度学习问题
geometric deep learning problem。 - 图的异质性
heterogeneity和多样性diversity:图本身可能很复杂,包含各种类型和属性。如,图可以是异质的或同质的、加权的或者不加权的、有向的或无向的。此外,图任务也有很大不同,包括node-level任务(如节点分类)、graph-level任务(如图分类)。这些不同的类型、属性、任务需要不同的模型架构来解决特定的问题。 - 大型图:大数据时代,真实的图很容易拥有数百万甚至数十亿个节点和边。一些著名的例子是社交网络和电商网络。因此如何设计可扩展
scalable的模型非常关键。 - 融合跨学科知识:图通常和其它学科联系在一起,如生物学、化学、社会科学。这种跨学科的性质带来了机遇和挑战:可以利用领域知识来解决特定问题,但是融合领域知识可以使得模型设计复杂化。如,当生成分子图时,目标函数和化学约束通常是不可微的,因此基于梯度的训练方法不容易应用。
为了应对这些挑战,人们在这一领域做出了巨大努力,诞生了很多有关论文和方法。论文
《Deep Learning on Graphs: A Survey》试图通过全面回顾图的深度学习方法来系统性总结不同方法之间的差异和联系。如下图所述,论文根据现有的模型架构和训练策略将这些方法分为五类:
- 图递归神经网络
graph recurrent neural networks: Graph RNN。 - 图卷积网络
graph convolutional networks: GCN。 - 图自编码器
graph autoencoders: GAE。 - 图强化学习
graph reinforcement learning: Graph RL。 - 图对抗方法
graph adversarial methods。
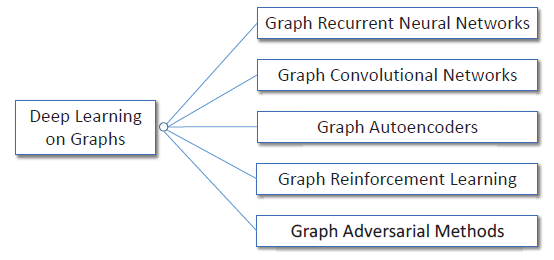
论文在下表中总结了这些方法之间的一些主要特点:
Graph RNN通过在node-level或者graph-level对状态建模从而捕获图的递归模式recursive pattern或者序列模式sequential pattern。GCN在不规则图结构上定义卷积和readout操作,从而捕获常见的局部结构模式和全局结构模式。GAE假设low-rank图结构,并采用无监督方法进行节点representation learning。Graph RL定义了graph-based动作和奖励,从而在遵循约束的同时获得图任务的反馈。- 图对抗方法采用对抗训练技术来提升
graph-based模型的泛化能力,并通过对抗攻击测试其鲁棒性。

- 图的不规则结构:和网格结构的图像、音频、文本数据不同,图数据具有不规则的结构,因此很难将一些基础的数学算子推广到图上。如,为图数据定义卷积、池化算法并不简单。这个问题通常被称作几何深度学习问题
相关工作:
之前的一些调综述与我们的论文有关:
《Geometric deep learning: going beyond euclidean data》总结了一些早期的GCN方法以及流形上的CNN,并通过几何深度学习geometric deep learning对其进行了全面的研究。《Relational inductive biases, deep learning, and graph networks》总结了如何使用GNN和GCN进行关系推理,使用了一个统一的框架,即graph network。《Attention models in graphs: A survey 》回顾了图的注意力模型。《Graph convolutional networks: Algorithms, applications and open challenges》总结了一些GCN模型。《Adversarial attack and defense on graph data: A survey》简要综述了图的对抗性攻击。
我们的工作与之前的这些工作不同,我们系统地、全面地回顾了图上不同的深度学习架构,而不是专注于一个特定的分支。
与我们的工作同时,
《Graphneural networks: A review of methods and applications》和《A comprehensive survey on graph neural networks》从不同的角度和分类对这个领域进行了综述。具体来说,他们的工作都没有考虑图强化学习或图对抗方法,而这些都是本文所涉及的。另一个密切相关的主题
graph embedding,目的是将节点嵌入到低维向量空间中。graph embedding和本文之间的主要区别是:我们专注于不同的深度学习模型如何应用于图,而graph embedding可以被认作是使用其中一些模型的具体应用实例。另外,graph embedding也可能使用非深度学习方法。
论文最后附录还给出了所有这些方法的源码地址、在公开数据集上的效果、时间复杂度。
1.1 基本概念
给定图
每个节点
每条边
定义
图可以为有向的或者无向的,可以为带权图或者无权图。
- 如果是有向图则
- 如果是带权图则
- 如果是有向图则
无向图的拉普拉斯矩阵定义为
degree矩阵。定义拉普拉斯矩阵的特征分解
eigen decomposition为:其中:
eigenvalue组成的对角矩阵。eigenvector组成的矩阵 。
定义转移概率矩阵为
定义
k-step邻域为:其中
dist(i,j)表示节点
对于深度学习方法,我们使用上标来区分不同的层
layer,如representation维度。通用的非线性激活函数记作
sigmoid激活函数记作relu激活函数记作除非另有说明,否则我们假设所有函数都是可微的,从而允许使用反向传播算法并使用常用的优化器和训练技术来学习模型参数。
如果使用采样技术,则采样大小记作
图上的深度学习任务大致可以分为两类:
node-level任务:这些任务和图中的各个节点有关,如节点分类、链接预测、节点推荐。graph-level任务:这些任务和整个图有关,如图分类、图属性预估、图生成。
1.2 Graph RNN
诸如
gated recurrent units: GRU或者long short-term memory: LSTM之类的循环神经网络是建模序列数据的事实标准。这里我们总结了可捕获图的递归和序列模式的Graph RNN。Graph RNN大致可以分为两类:node-level RNN和graph-level RNN。主要区别是通过节点状态对node-level模式建模,还是通过公共的图状态对graph-level模型建模。下表给出了这些方法的主要特点。
1.2.1 node-level RNN
图的
node-level RNN,也称作图神经网络graph neural networks: GNNs,其背后思想很简单:每个节点受递归神经网络启发,
GNN采用了状态的递归定义:其中
一旦得到
对于
graph-level任务,作者建议添加一个具有唯一属性的特殊节点来代表整个图。为学习模型参数,作者使用以下半监督方法:
- 使用
Jacobi方法将状态方程(即定义stable point。 - 使用
Almeida-Pineda算法执行一个梯度下降step。 - 最小化
task-specific目标函数,如针对回归任务的平方损失。 - 重复上述过程直到模型收敛。
GNN通过上述两个简单方程,发挥了两个重要作用:GNN统一了一些处理图数据的早期方法,如RNN和马尔科夫链。GNN的基本概念具有深远启发,许多最新的GCN实际上都有类似于状态方程的公式。
尽管
GNN在概念上很重要,但是它仍然存在一些缺陷:为确保状态方程具有唯一解,
contraction map。即,直观地看,收缩映射要求任意两个点之间的距离在经过
在梯度下降的
step之间,需要多轮迭代才能够收敛到不动点,因此GNN的计算量很大。
由于存在这些缺陷,并且当时算力不高(
GPU在当时并未被广泛应用于深度学习),以及缺乏研究兴趣,当时GNN并未成为研究重点。- 使用
对
GNN的显著改进是gated graph sequence neural networks:GGS-NNs。在GGS-NNs中,作者使用GRU替代了状态方程中的递归定义,因此移除了收缩映射的约束,并支持了现代优化技术。具体而言,状态方程修改为:
其中
然后作者提出依次使用若干个这种网络,从而产生序列输出,表明这种方法可以应用于序列任务。
SSE采用了类似于GGS-NNs的方法,但是并未使用GRU,而是采用随机固定点梯度下降stochastic fixed-point gradient descent,从而加快训练过程。这种方案基本上是在使用局部邻域计算不动点状态、优化模型参数之间交替进行。这两种计算都是在
mini-batch中进行的。
1.2.2 graph-level RNN
在
Graph-level RNN中,不是将单个RNN应用于每个节点以学习节点状态,而是将单个RNN应用于整个图从而对图状态进行编码。《GraphRnn:Generating realistic graphs with deep auto-regressive models》将Graph RNN用于图生成问题。具体而言,他们采用两种RNN:一种用于生成新节点,另一种用于以自回归的方式为新添加的节点生成边。他们表明:这种层次
hierarchical的RNN体系结构比传统的、基于规则的图生成模型更有效地从输入图中学习,同时具有合理的时间复杂度。为捕获动态图的时间信息,
DGNN使用时间感知time-aware的LSTM来学习node representation。当建立新的边时,
DGNN使用LSTM更新这条边的两个交互节点以及它们直接邻居的representation,即考虑一阶传播效果。作者表明:time-aware LSTM可以很好地建模边生成的顺序establishing order和时间间隔time interval,从而有助于一系列图的应用。Graph RNN也可以和其它架构(如GCN/GAE)组合。- 如,为解决稀疏性问题,
RMGCNN将LSTM应用于GCN的结果,从而逐渐重建reconstruct图。通过使用LSTM,来自图不同部分的信息不需要很多GCN层就可以传递到很远的距离。 Dynamic GCN使用LSTM来聚合动态网络中不同时间片的GCN结果,从而捕获时空图spatial and temporal graph的信息。
- 如,为解决稀疏性问题,
1.3 GCN
类似
CNN, 现代GCN通过精心设计的卷积函数和readout函数来学习图的常见局部结构模式和全局结构模式。由于大多数
GCN可以使用task-specific损失函数(只有少数例外,如无监督学习方法),并通过反向传播进行训练。因此这里我们仅讨论体系结构。下表给出了我们总结的
GCN的主要特征。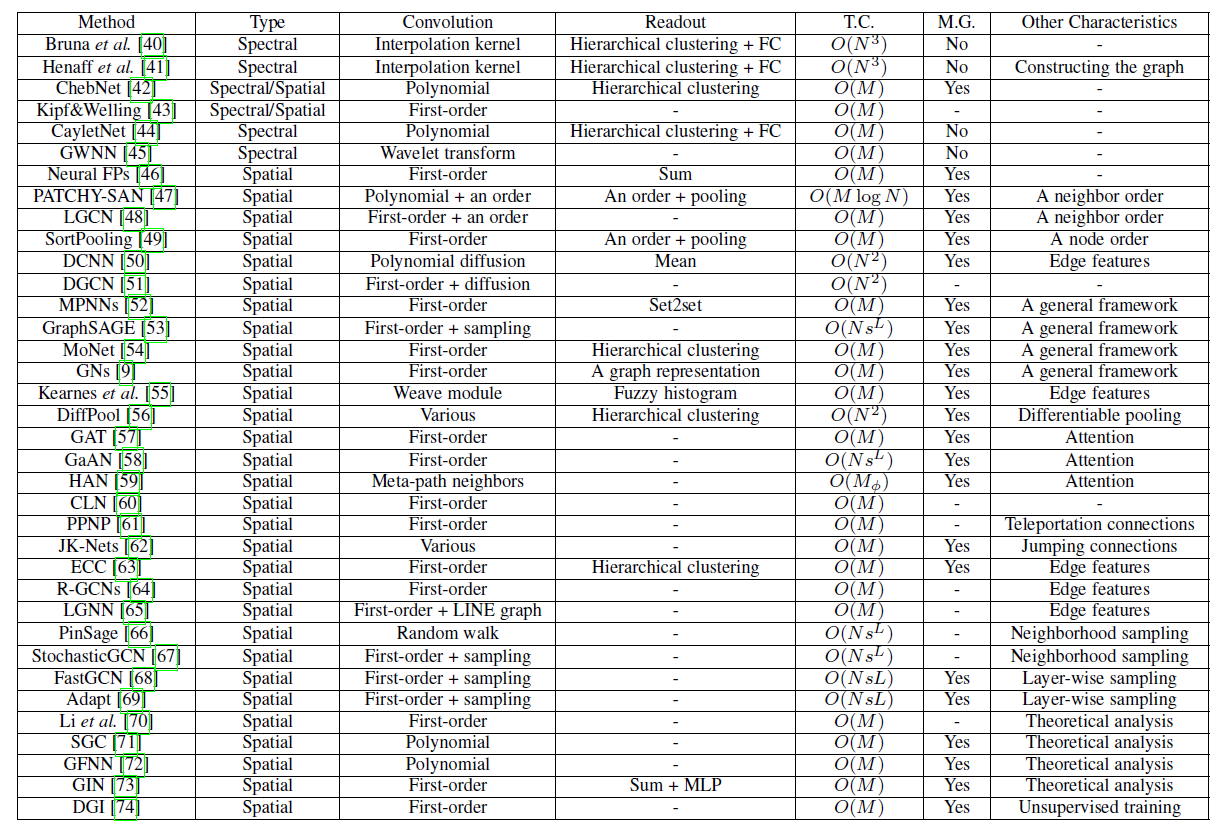
1.3.1 卷积操作
卷积操作可以分为两类:
- 谱域卷积
spectral convolution:卷积操作通过使用图傅里叶变换将node representation转换到谱域spectral domain中进行卷积。 - 空域卷积
spatial convolution:卷积操作使用邻域节点进行卷积。
注意,这两种卷积可以重叠
overlap,如使用多项式谱域卷积核polynomial spectral kernel时。- 谱域卷积
a. 谱域卷积
卷积是
CNN中最基本的操作,但是用于图像或文本的标准卷积算子无法直接应用于图,因为图没有网格结构。《Spectral networks and locally connected networks on graph》首先使用图拉普拉斯矩阵basis相似的作用。定义图卷积算子
其中
eigenvector组成的矩阵 ,简而言之:
- 通过左乘
spectral domain,即图傅里叶变换Graph Fourier Transform。 - 通过左乘
spatial domain,即傅里叶逆变换。
该定义的有效性基于卷积定理,即卷积运算的傅里叶变换是其傅里叶变换的逐元素乘积。
定义谱域卷积核为
eigenvalue因此作用在输入信号
其中
通过将不同的卷积核应用于不同的
input-output信号来定义卷积层,即:其中:
hidden representation的维度。hidden representation向量在第
上式背后的思想和传统的卷积类似:它使输入信号通过一组可学习的滤波器,从而聚合信息,然后进行一些非线性变换。通过使用节点特征矩阵
CNN。理论分析表明:图卷积运算的这种定义可以模拟CNN的某些几何特性。但是,直接使用上式需要学习
localized in the spatial domain,即在谱域卷积中,每个节点都会受到全局所有节点的影响(而不是仅受到局部邻域节点的影响)。为缓解这些问题《Spectral networks and locally connected networks on graphs》建议使用以下平滑滤波器smoothing filters:其中
fixed interpolation kernel,但是还有两个基本问题尚未解决:
- 首先,每次计算都需要拉普拉斯矩阵的完整特征向量
eigenvectors,因此每次前向传播、反向传播的时间复杂度至少为 - 其次,由于滤波器取决于图的傅里叶基
basis
- 通过左乘
有一些
GCN模型用于解决上述的第一个问题,即计算效率方向。为解决计算效率问题,
ChebNet提出使用多项式滤波器,即:其中:
然后作者使用切比雪夫多项式展开来代替矩阵的特征分解:
其中:
由于切比雪夫多项式的正交基的要求,这里重新缩放是有必要的。
根据
其中
根据切比雪夫多项式的递归定义,有:
因此有:
现在仅需要计算稀疏矩阵
另外,也很容易看到这种多项式滤波器是严格地
representation仅受到它《Semi-supervised classification with graph convolutional networks》进一步仅使用一阶邻域来简化滤波器:其中:
degree。representation,representation向量的维度。
将其写作矩阵形式为:
其中
degree矩阵。作者表明:通过设置
ChebNet滤波器等价于上式。作者认为,如下图所述堆叠足够多的卷积层具有类似于ChebNet的建模能力,并且会带来更好的效果。下图中,每个节点仅被它们的直接邻居所影响。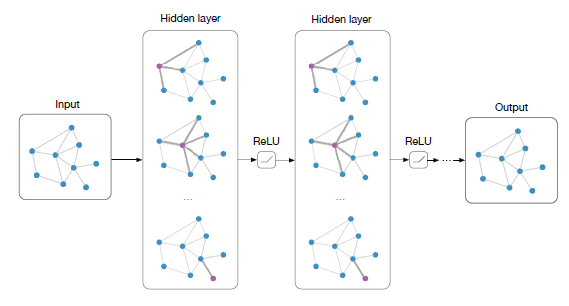
ChebNet及其扩展方法的重要洞察insight是:它们将谱域图卷积和空间结构联系在一起。具体而言,它们表明:当谱域卷积为多项式时(一阶多项式也是一种多项式),谱域卷积等价于空间卷积。另外,卷积公式
GNN中的状态定义GNN可以被视为具有大量identical layer(即层与层之间都相同的)以达到稳定状态的GCN。例如,GNN使用固定参数的固定函数来迭代更新节点的hidden state,直到达到状态平衡为止。而GCN具有预设的层数,并且每层使用不同的参数。还有一些谱域方法解决效率问题。如
CayleyNet并未使用切比雪夫多项式展开,而是采用Cayley多项式来定义图卷积:其中
除了证明
CayLeyNet的效率和ChebNet一样,作者还证明了Caylay多项式可以检测narrow frequency bands of importance从而获得更好的效果。Graph wavelet neural network:GWNN通过重写公式其中
graph wavelet的基bases。通过使用快速近似算法来计算
GWNN的计算复杂度也是
有一些
GCN模型用于解决上述的第二个问题,即跨图的泛化。Neural FPs也提出一种使用一阶邻域的空间卷积方法:由于参数
Neural FP可以处理任意大小的多个图。注意这里degree不同而不同。上式和
《Semi-supervised classification with graph convolutional networks》提出的滤波器非常相似,区别在于:Neural FP不是通过添加归一化项来考虑节点degree的影响,而是为不同degree的节点学习不同的参数。该策略对于较小的图(如分子图)效果很好,但是无法扩展到更大的图。PATCHY-SAN使用诸如Weisfeiler-Lehman kernel之类的图labeling过程为节点分配了唯一的节点顺序,然后使用这个预分配的顺序将节点邻居排列。然后
PATCHY-SAN通过从节点的receptive field。最后,
PATCHY-SAN采用一个标准的、带适当normalization的一维CNN到这个感受野上。通过这种方式,不同的图中的节点都具有固定大小和顺序的感受野,因此
PATCHY-SAN可以从多个图中学习,就像正常的CNN从多个图像中学习一样。这种方式的缺点是卷积在很大程度上依赖于图
labeling过程,而图labeling过程是一个预处理步骤,它并不是学习的一部分(即没有可学习的参数)。LGCN进一步提出通过按字典顺序简化排序过程。即根据邻居在最后一层hidden representationSortPooling采用了类似的方法,但是它并不是对每个节点的邻居进行排序,而是对所有节点进行排序。即所有节点的所有邻域的排序都相同。
尽管这些方法之间存在差异,但是对于图来说,强制采用一维节点顺序可能不是很自然的选择。
GCNN采用diffusion-basis来代替图卷积中的eigen-basis,即节点的邻域由节点之间的扩散转移概率diffusion transition probability来决定。具体而言,卷积定义为:
其中
但是,计算
DGCN通过一个对偶图卷积dual graph convolutional框架来同时使用diffusion base和adjacent base。具体而言,DGCN使用两个卷积:一个是邻接矩阵的形式:
另一个是将转移概率中的邻接矩阵转换为
pointwise mutual information:PPMI:其中
PPMI矩阵:degree矩阵。
然后
DGCN通过最小化ensemble这两个卷积。DGCN通过随机游走采样技术来加速转移概率的计算。实验表明:这种对偶卷积甚至对于单图问题single-graph problem也是有效的。
b. 空域卷积
基于谱域卷积的工作,
《Neural message passing for quantum chemistry 》提出了MPNNs为图的空域卷积提出了一个统一的框架,它使用消息传递函数message-passing function:其中:
从概念上讲
MPNN是一个框架,在该框架中,每个节点都根据其状态发送消息,并根据从直接邻居中收到的消息来更新节点状态。作者表明:上述框架已经包含了很多现代方法,如GGSNNs、Neural FPs等都是特例。另外,作者建议添加一个
master节点,该节点连接图中所有其它节点从而加速长程消息传递。并且作者拆分hidden representation到不同的tower来提高泛化能力。作者表明:MPNNs的特定变体可以在预测分子特性方面达到state-of-the-art性能。GraphSAGE采用类似message-passing function的思想,它使用聚合函数:其中
AGG(.)表示聚合函数。作者提出三个聚合函数:均值池化、
LSTM、最大池化。例如对于最大池化有:其中
对于
LSTM聚合函数,由于需要确定邻域顺序,因此作者采用了最简单的随机顺序。Mixture model network:MoNet也尝试使用 “模板匹配“template matching” 将现有的GCN模型以及用于流形manifold的CNN模型统一到一个通用框架中:其中:
pair对pseudo-coordinates,定义为:其中
degree。
换句话讲,
kernel。然后MoNet采用以下高斯核:其中
Graph Network:GNs提出了一个比GCNs、GNNs更通用的框架,它学习三组representation:分别代表节点
embedding、边embedding、整个图的embedding。这些
representation通过三个聚合函数、三个更新函数来学习:其中:
注意:消息传递函数都是以集合作为输入,因此它们的参数是可变数量的。因此这些消息传递函数对于输入的不同排列应该是不变的。一些排列不变的函数包括逐元素求和、均值池化、最大池化。
和
MPNN相比,GNs引入了边的representation和全图representation,从而使得框架更加通用。总而言之,卷积运算已经从谱域发展到频域,并从
k-hop邻域发展到直接邻域。目前,从直接邻域收集消息,如message-passing function、GraphSAGE aggregating functions、GNet aggretation/ update functions是图卷积运算最常见的选择。
1.3.2 Readout 操作
使用图卷积操作可以学到有效的节点
representation从而解决node-level任务。但是,为处理graph-level任务,需要聚合节点信息来构成graph-level representation。在文献中,这种聚合过程被称作readout操作。基于规则的局部邻域,标准的
CNN可以执行步长大于1的卷积或池化操作来逐渐降低分辨率,从而得到graph-level representation。而图缺乏网格结构,因此无法直接应用现有的这些方法。顺序不变性
order invariance:图的readout操作的关键要求是该操作不应依赖于节点顺序。即,如果我们改变节点编号和边的编号(编号改变意味着顺序改变),则整个图的representation不应改变。例如,一种药物是否可以治疗某些疾病取决于其固有结构,和我们对节点的编号顺序无关。如果我们采用不同的编号顺序,则应该得到相同的结果。
注意:
- 这个问题和图同构
isomorphism问题有关,其中最著名的算法是拟多项式的quasipolynomial,所以我们只能找到多项式时间内order-invariant的函数。 - 同构的两个图得到相同的
representation,反之不一定成立。即相同representation的两个图不一定是同构的 。
- 这个问题和图同构
统计量:最常见的顺序无关算子包括简单的统计量
statistics,如求和、均值池化、最大池化:其中:
representation;representation。这种一阶统计量虽然简单,但是不足以刻画不同的图结构。
论文
《Molecular graph convolutions: moving beyond fingerprints》建议通过使用模糊直方图fuzzy histograms来考虑节点representation的分布。模糊直方图背后的基本思想是:构建几个直方图分桶
histogram bins,然后计算representation作为样本,将它们和一些预定义的模板(每个模板代表一个分桶)进行匹配,最后返回最终直方图的拼接concatenation。通过这种方式,可以区分具有相同的sum/average/maximum、但是具有不同节点分布的图。在论文
《Spectral networks and locally connected networks on graphs 》中,作者采用了常用的一种方法:添加一个全连接层FC作为final layer:其中
上式可以视为
node-level representation的加权和。优点之一是该模型可以为不同节点学习不同的加权权重。但是,这种能力是以无法保证顺序不变性为代价的。
层次聚类:实际上图具有丰富的层次结构,而不仅仅是
node-level、graph-level这两层结构。可以通过层次聚类hierarchical clustering的方式来探索图的层次结构,如下图所示。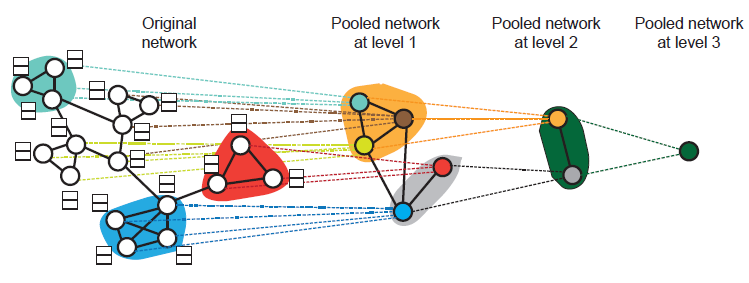
《Spectral networks and locally connected networks on graphs》使用了基于密度的agglomerative聚类,《Deep convolutional networks on graph-structured data》使用了多分辨率谱聚类。ChebNet和MoNet使用了另一种贪婪的层次聚类算法Graclus来一次合并两个节点,并采用了一种快速池化的方法将节点重新排列为平衡二叉树。ECC通过执行特征分解来使用另一种层次聚类方法。但是,这些层次聚类方法都和图卷积无关,而是作为预处理步骤进行的,并且无法以端到端的方式进行训练。
为解决这个问题,
DiffPool提出了一种与图卷积联合训练的、可微的层次聚类算法。具体而言,作者提出使用hidden representation来学习每个层次中的soft cluster assignment矩阵。其中:
cluster assignment矩阵,hidden representation。
然后根据
coarsened图的node representation和新的邻接矩阵:其中
因此,在
DiffPool中每一层的卷积操作之后,图从cluster assignment操作是soft的,因此簇之间的连接并不是稀疏的,因此该方法的时间复杂度原则上为
强加顺序:如前所述,
PATCHY-SAN和SortPooling采用强加节点顺序impose order的思想 ,然后像CNN一样采用标准的一维池化。这些方法是否可以保留顺序不变性,取决于强加顺序的方式,这是另一个研究领域。除了强加节点顺序之外,还有一些启发式方法。在
GNN中,作者建议添加一个连接到所有节点的特殊节点从而代表整个图。同样地,GNs提出通过从所有节点和所有边接收消息来直接学习整个图的representation。MPNNs采用set2set,这是对seq2seq模型的修改。具体而言,set2set使用Read-Process-Write模型,该模型同时接收所有输入,使用attention机制和LSTM计算内部状态,然后写入输出。和
seq2seq的顺序敏感性不同,set2set对于输入是顺序不变的。简而言之,诸如均值、求和之类的统计量是最简单的
Readout操作,而通过图卷积联合训练的层次聚类算法更加先进、也更复杂。还有一些其它的方法,如添加虚拟节点来代表图、或强加节点顺序。
1.3.3 改进
已有很多技术用于进一步改善
GCN。注意,其中一些方法是通用的,也可以应用于图上的其它深度学习模型。attention机制:上述GCN中,邻域节点以相等或预定义的权重进行聚合。但是邻域节点的影响力可能差异很大,因此应该在训练过程中学习它们,而不是预先确定。受注意力机制的启发,图注意力网络
graph attention network:GAT通过修改GCN:其中
其中
MLP。可以看到
为提高模型的容量和稳定性,作者还提出使用多个独立的注意力,并将其结果进行合并。即下图所述的多头注意力机制
multi-head attention mechanism。每种颜色代表不同的、独立的注意力向量。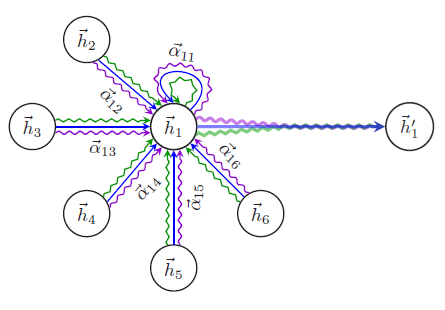
GaAN进一步提出针对不同的head学习不同的权重,并将这种方法应用于交通预测问题。HAN提出针对异质图的two-level注意力机制,即node-level注意力和semantic-level注意力。具体而言:node-level注意力机制类似于GAT,但是也考虑了节点类型。因此它可以分配不同的权重来聚合metapath-based邻域。- 然后,
semantic-level注意力机制学习不同metapath的重要性,并输出最终结果。
残差和跳跃连接:很多研究观察到,现有
GCN最合适的深度通常非常有限,如2层或3层。这个问题可能是由于训练深层GCN时比较困难,或者过度平滑over-smoothing问题导致。过度平滑问题是指:深层GCN中,所有节点都具有相同的representation。为解决这些问题,可以考虑将类似
ResNet的残差连接添加到GCN中。《Semi-supervised classification with graph convolutional networks》在公式residual connection:他们通过实验表明:通过添加此类残差连接可以使得网络深度更深,这和
ResNet结果类似。Column network:CLN采取了类似的思想,它使用以下具有可学习权重的残差连接:其中
其中
注意:
GGS-NNs中的GRU。区别在于:这里的上标表示层数,不同的层包含不同的参数;在GRU中上标表示时间,并且跨不同时间步共享同一组参数。受到
personalized PageRank启发,PPNP定义如下的卷积层:其中
注意:
PPNP的所有参数都在JK-Net提出另一种体系结构,它将网络的最后一层和所有较低的hidden layer相连,即通过将所有representation跳跃到最终输出,如下图所述。这样,模型可以自适应地学习利用来自不同层的信息。正式地,
JK-Net定义为:其中:
representation。JK-Net使用三个类似于GraphSAGE的聚合函数:拼接concatenation、最大池化max-pooling、LSTM attention。
实验结果表明:添加跳跃连接可以提高
GCN的性能。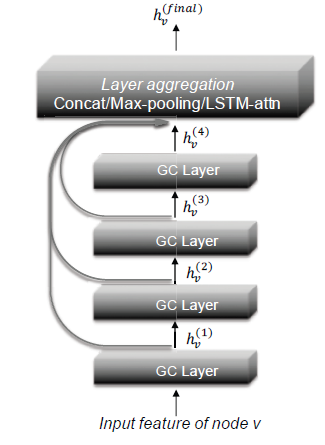
edge特征:前面提到的GCN大多数聚焦于利用节点特征和图结构,这里我们讨论如何利用另一个重要的信息源:边特征。对于具有离散值(如边类型)的简单边特征,一种直接的方法是为不同的边类型训练不同的参数,然后对结果进行聚合。
Neural FPs为不同degree的节点训练了不同的参数,这对应于分子图中不同化学键类型的隐式边特征,然后对结果进行求和。CLN在异质图中为不同的边类型训练不同的参数,然后对结果取均值。Edge-conditioned convolution:ECC也基于边类型训练了不同的参数,并将其应用于图分类。Relational GCNs: R-GCNs通过为不同的关系类型训练不同的权重,对知识图谱采用了类似的方法。
但是这些方法仅适用于有限数量的、离散的边特征
discrete edge feature。DCNN将每条边转换为一个节点,该节点和该边的head node, tail node相连。进行转换之后,可以将边特征视为节点特征。LGCN构建一个线性图line graph即
然后
LGCN采用两个GCN:一个位于原始图上、另一个位于线性图上。《Molecular graph convolutions: moving beyond fingerprints》提出了一个使用weave module的架构。具体而言,他们学习了节点和边的representation,并使用四个不同的函数在每个weave module中交换它们之间的信息:节点到节点node-to-node:NN、节点到边node-to-edge:NE、边到边edge-to-edge:EE、边到节点edge-to-node:EN。其中:
representation。
通过堆叠多个这样的
module,信息可以在节点representation和边representation之间交替传递。注意:在节点到节点的函数、边到边的函数中,隐式添加了
JK-Nets相似的跳跃连接。GNs还提出了学习边的representation,并通过消息传递函数来同时更新node representation和edge representation。这这一方面,weave module是GNs的特例,这个特例并不学习整个图的representation。
采样:在大型图上训练
GCN时,关键的瓶颈之一是计算效率。如前所述,许多GCN采用邻域聚合方案。但是,由于很多真实场景的图遵循幂律分布power-low distribution,其中少量节点的degree非常大、大量节点的degree非常小,因此不同节点的邻域规模差异很大。为解决这个问题,已经提出两种类型的采用方法:邻域采样
neighborhood samplings、逐层采样layer-wise samplings。如下图所示,其中蓝色节点表示一个batch的样本,箭头表示采样方向,B中的红色节点表示历史采样样本。在邻域采样中,
GCN在计算期间对每个节点执行采样。GraphSAGE在训练期间为每个节点统一采样固定数量的邻居。PinSage提出在图上使用随机游走对邻域进行采样,同时还有一些实现方面的改进,包括CPU和GPU之间的协同、一个map-reduce inference pipeline等。PinSage被证明能够处理真实的、十亿级的图。StochasticGCN进一步提出通过使用上一个batch的历史激活作为控制变量来降低采样方差,从而理论上保证可以使用任意小的采样数量。
FastGCN并没有对节点的邻域进行采样,而是在每个卷积层中对所有节点进行采样,即layer-wise采样。FastGCN将节点解释为独立同分布的样本,并将图卷积解释为概率测度下的积分变换。FastGCN还显示:通过归一化degree来采样节点可以降低方差并提高模型性能。《Adaptive sampling towards fast graph representation learning》进一步提出基于更高一层layer为条件来采样更第一层layer的节点,从而更加自适应,并显著降低方差。
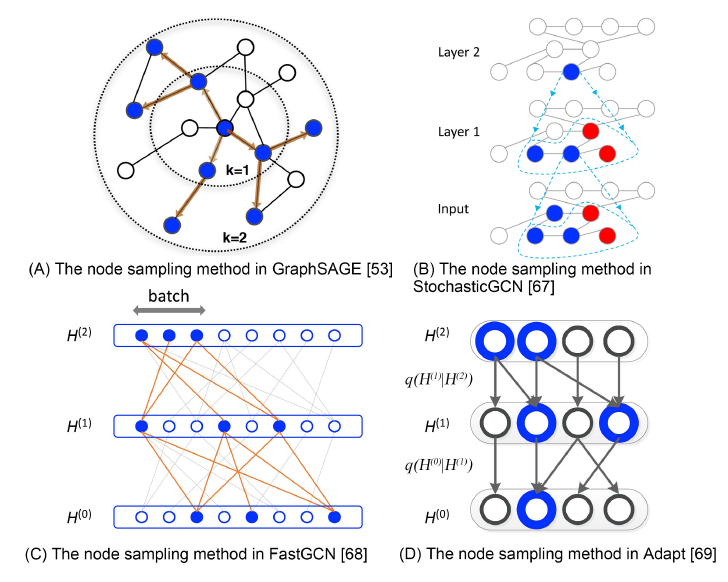
inductive learning:GCN模型的一个重要特点是,它是否可以应用于inductive learning。即在一组节点或图上进行训练,并在另一组未见过的节点或图上进行测试。原则上,这个目标是通过学习给定特征上的映射函数来实现的,其中给定的特征不依赖于图结构,使得这个映射函数可以迁移到未见过的节点或图上。
inductive learning已经在GraphSAGE、GAT、GaAN、FastGCN中得到了验证。但是,现有的inductive GCN仅适用于具有显式特征的图,如何对没有显式特征的图(通常称作样本外问题out-of-sample problem)进行inductive learning仍然是悬而未决的。
1.3.4 理论分析
为理解
GCN的有效性,人们提出了一些理论分析,可以分为三类:node-level任务、graph-level任务、一般性分析。node-level任务:《Deeper insights into graph convolutional networks for semi-supervised learning》首先通过使用特殊形式的拉普拉斯平滑分析了GCN的性能:拉普拉斯平滑使得同一个簇内的节点的representation相似。原始拉普拉斯平滑操作如下:
其中
representation,representation。可以看到拉普拉斯平滑非常类似于卷积公式
GCN的Co-Training和Self-Training方法。最近
《Simplifying graph convolutional networks》从信号处理的角度分析了GCN。通过将节点特征视为图信号,他们表明公式利用这一洞察,他们提出了
simplified graph convolution:SGC方法,该方法消除所有非线性并将所有待学习的参数收缩collapsing到一个矩阵:作者表明:这种
non-deeplearning的GCN变体可以在很多任务上达到与现有GCN匹配的性能。《Revisiting graph neural networks: All we have is low-pass filters》通过证明低通滤波操作并没有为GCN配备非线性流形学习能力来强化这一结果,并进一步提出GFNN模型来解决这个额外的难题,方法是在图卷积层之后添加一个MLP层。
graph-level任务:《Semi-supervised classification with graph convolutional networks》和SortPooling都考虑GCN和graph kernel(如Weisfeiler-Lehman:WL的kernel)之间的联系,其中graph kernel广泛用于图同构测试graph isomorphism tests。他们表明:从概念上讲
GCN是WL kernel的泛化,因为这两种方法都会迭代地聚合来自节点领域的信息。《How powerful are graph neural networks?》通过证明WL kernel在区分图结构方面为GCN提供了上限,从而形式化了这一思想。基于该分析,他们提出了
graph isomorphism network:GIN,并表明使用一个基于求和的Readout操作、一个MLP就可以实现最大判别能力,即在graph classification任务中具有最高的训练accuracy。
一般性分析:
《The vapnik–chervonenkis dimension of graph and recursive neural networks》表明:具有不同激活函数的GCN的VC-dim具有与RNN相同的规模。《Supervised community detection with line graph neural networks》分析了线性GCN的优化情况,并表明在某些简化下,任何局部极小值都接近于全局最小值。《Stability and generalization of graph convolutional neural networks》分析了GCN的算法稳定性和泛化界。他们表明:如果图卷积滤波器的最大绝对特征值和图大小无关,则单层
GCN会满足均匀稳定性uniform stability的强概念。
1.4 Graph AutoEncoder
自编码器
autoencoder:AE及其变体已经被广泛应用到无监督学习任务中,它适用于学习图的节点representation。其背后隐含的假设是:图具有固有inherent的、潜在potentially的非线性低秩结构。这里我们首先介绍图自编码器
graph autoencoder:GAE,然后介绍图变分自编码器graph variational autoencoder以及其它改进。下表总结了GAE的主要特点,其中TC表示时间复杂度。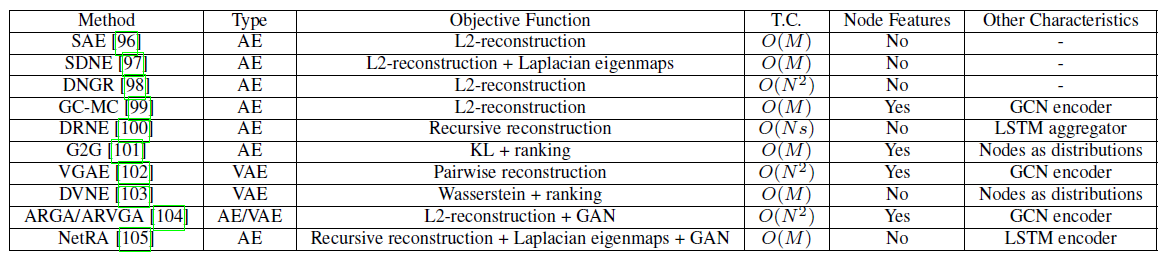
1.4.1 图自编码器
图自编码器起源于稀疏自编码器
sparse autoencoder:SAE,其基本思想是:将邻接矩阵或其变体视为节点的原始特征,然后利用自编码器作为降维技术来学习节点representation。具体而言,
SAE使用了如下的其中:
representation向量,representation向量维度。MLP。
换句话讲,
SAE通过编码器将另外,还可以在损失函数中添加一个正则化项。
在获得低维
representationk-means算法来用于节点聚类。实验表明:
SAE优于非深度学习baseline。但是,SAE是基于不正确incorrect的理论分析,其有效性的底层机制仍然无法解释。Structure deep network embedding:SDNE解决了这个问题。SDNE表明:second-order proximity。即,如果两个节点共享相似的邻域,则它们应该具有相似的潜在表示。这是network science中被深入研究的概念,被称作协同过滤或三角闭合triangle closure。由于
network embedding方法表明一阶邻近度也很重要,因此SDNE通过添加另一个拉普拉斯特征图Laplacian Eigenmap项来调整目标函数:即:如果两个节点直连,则它们也共享相似的潜在表示。
作者还通过使用邻接矩阵来修改
其中:
- 当
SDNE整体架构如下图所示,它通过deep autoencoder来保持节点之间的一阶邻近度和二阶邻近度。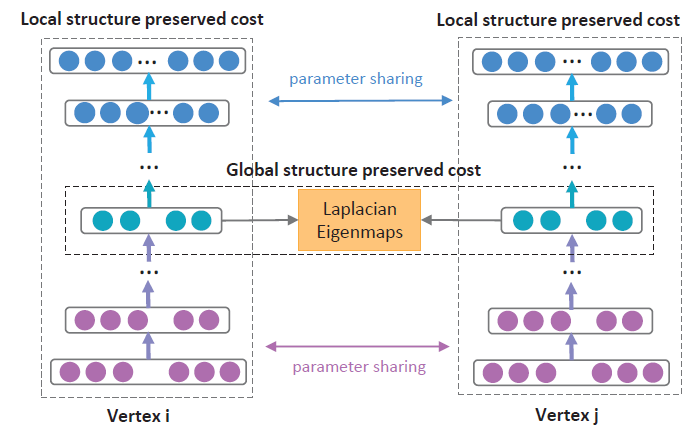
DNGR使用positive pointwise mutual information: PPMI代替转移概率矩阵GC-MC采用了不同的方法,它使用GCN来作为编码器:然后使用一个简单的
bilinear函数作为解码器:其中
通过这种方式,可以很自然地融合节点特征。对于没有节点特征的图,可以使用节点
ID的one-hot向量。作者证明了GC-MC在二部图推荐问题上的有效性。DRNE并没有重构邻接矩阵或其变体,而是提出了另一种思路:通过LSTM聚合邻域信息来直接重构低维节点embedding向量。具体而言,DRNE采用以下目标函数:由于
LSTM要求输入为序列,因此作者建议根据邻域内每个邻居节点的degree对邻居节点进行排序。作者还对具有较大degree的节点采用邻域采样技术,从而防止序列太长。作者证明:
DRNE可以保留regular equivalence,以及节点的很多centrality measure,如PangeRank。与上述将节点映射为低维向量的工作不同,
Graph2Gauss:G2G提出将每个节点编码为高斯分布具体而言,作者使用从节点属性到高斯分布的均值、方差的深度映射作为编码器:
其中
然后,它们使用
pairwise约束来学习模型,而不是使用显式的解码器函数:其中:
Kullback-Leibler: KL距离。
换句话讲,约束条件确保
node representation之间的KL距离和图中节点之间距离保持相同的相对顺序。但是,由于上式难以优化,因此作者采用基于能量的损失函数作为松弛:
其中:
KL距离。
作者进一步提出了无偏的采样策略,从而加快训练过程。
1.4.2 变分自编码器
与上述自编码器不同,变分自编码器
variational autoencoders:VAE是将降维技术和生成模型结合在一起的另一种深度学习方法。它的潜在优点包括对噪声容忍、以及能够学习平滑的representation。VAE首次被引入图数据是在VAGE,其中解码器是简单的线性内积:其中节点
representation假设服从高斯分布:作者使用
GCN作为均值和方差的编码器:然后通过最小化变分下界
variational lower bound来学习模型参数:但是该方法需要重构完整的图,因此时间复杂度为
受到
SDNE和G2G启发,DVNE为图数据提出了另一种VAE,它也将每个节点表示为高斯分布。和现有的采用KL散度作为距离度量不同,DVNE使用Wasserstein距离来保留节点相似度的传递性transitivity。和
SDNE、G2G相似,SVNE在目标函数中保留了一阶邻近度和二阶邻近度:其中:
Wasserstein距离。ranking loss。
重构损失定义为:
其中
通过这种方法,目标函数可以像传统
VAE中使用reparameterization技巧一样被最小化。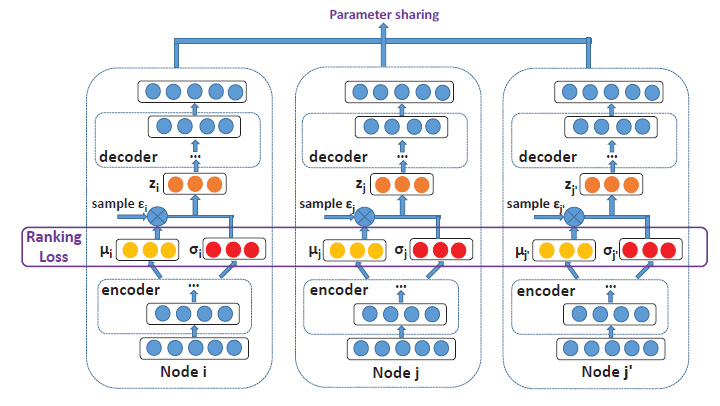
1.4.3 改进
对抗训练:
ARGA通过在GAE中添加一个额外的正则化项,从而引入了对抗训练adversarial training。其总体架构如下图所示。具体而言,
GAE编码器用作生成器generator,而判别器discriminator目标是区分潜在representation是来自生成器还是来自先验分布。通过这种方式,自编码器被迫匹配先验分布,这相当于是一个正则化。ARGA的目标函数是:其中
GAE中的重构损失,而其中:
VAGE中的图卷积编码器。
实验结果证明了对抗训练方案的有效性。
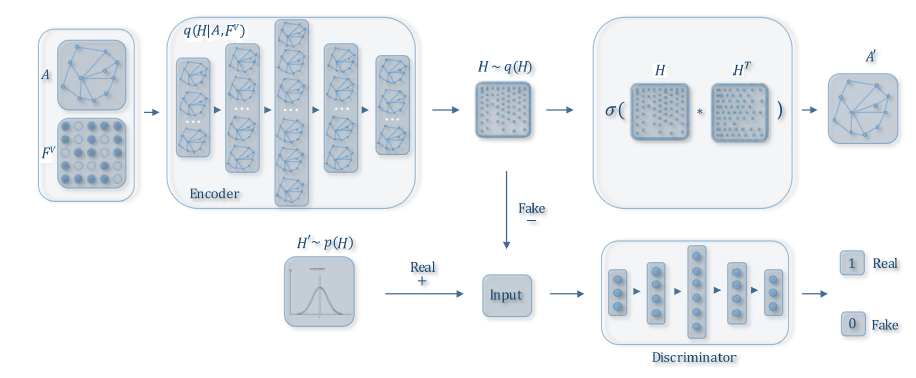
同一时期,
NetRA也提出了一个生成对抗网络generative adversarial network:GAN来提升图自编码器的泛化能力。作者使用如下的目标函数:其中:
GAE中的重构损失。
此外,作者使用
LSTM作为编码器,从而聚合邻域信息。NetRA并没有像DRNE中那样仅对直接邻居进行采样并使用degree对直接邻居进行排序,而是使用了随机游走来生成输入序列。和
ARGA相比,NetRA认为GAE的representation是ground-truth,并使用随机高斯噪声然后接一个MLP作为生成器。
inductive learning:和GCN相似,如果将节点属性融合到编码器中,则GAE可以应用于inductive learning。 这可以通过使用GCN作为编码器来实现,如在GC-MC, VGAE中。也可以通过直接学习一个从节点特征到
embedding的映射函数来实现,如G2G。由于仅在学习参数时才用到边信息,所以该模型也可以应用于训练期间未曾见过的节点。这些工作还表明,尽管
GCN和GAE基于不同的架构,但是它们可以组合使用。我们认为这是未来一个有希望的方向。相似性度量:在
GAE中已经采用了很多相似性度量,如:- 图自编码器:
L2重构损失、拉普拉斯特征图损失、ranking loss。 - 图变分自编码器:
KL距离、Wasserstein距离。
尽管这些相似性度量基于不同的动机,但是如何为特定的任务和模型体系结构选择合适的相似性度量仍然未被研究。需要更多的研究来了解这些度量指标之间的根本差异。
- 图自编码器:
1.5 Graph RL
众所周知,强化学习
reinforcement learning:RL善于从反馈中学习,尤其是在处理不可微的目标和约束时。这里我们回顾了Graph RL方法,如下表所示。
GCPN利用RL生成目标导向的goal-directed分子图,同时考虑了不可微的目标函数和约束。具体而言,它将图生成过程建模为添加节点和边的马尔可夫决策过程,并将生成模型视为在图生成环境中运行的
RL agent。通过将agent action视为链接预测、使用domain-specific以及对抗性奖励、使用GCN来学习节点representation,该方法可以使用策略梯度以端到端的方式训练GCPN。同一时期的
MolGAN采用了类似的思想,即使用RL生成分子图。但是,MolGAN提出不要通过一系列action来生成图,而是直接生成完整的图。这种方法对于小分子特别有效。GTPN采用RL预测化学反应产物。具体而言,该agent的action是选择分子图中的节点pair对,然后预测它们新的化学键的类型。根据预测是否正确,从而对agent进行实时奖励以及最终奖励。GTPN使用GCN来学习节点representation,以及一个RNN来记住memorize预测序列。GAM通过使用随机游走将RL应用于图分类。作者将随机游走建模为部分可观测的马尔可夫决策过程partially observable Markov decision process:POMDP。agent执行了两项操作:- 首先,它预测了图的标签。
- 然后,它选择随机游走中的下一个节点。
奖励的确定仅取决于
agent是否对图进行了正确的分类:其中:
time step;DeepPath和MINERVA都是采用RL对知识图谱knowledge graph: KG进行推理。具体而言,
DeepPath的目标是寻找路径,即在两个目标节点之间找到信息量最大的路径;而MINERVA则处理问答任务,即在给定问题节点和关系的情况下找到正确的答案节点。这两种方法中,
RL agent都需要在每个step中预测路径中的下一个节点,并在KG中输出推理路径。如果路径正确地到达了目的地,则agent获得奖励。DeepPath还添加了正则化项来鼓励路径多样性。
1.6 Graph Adversarial
这里我们介绍如何将对抗方法
adversarial method应用到图,下表给出了图对抗方法的主要特点: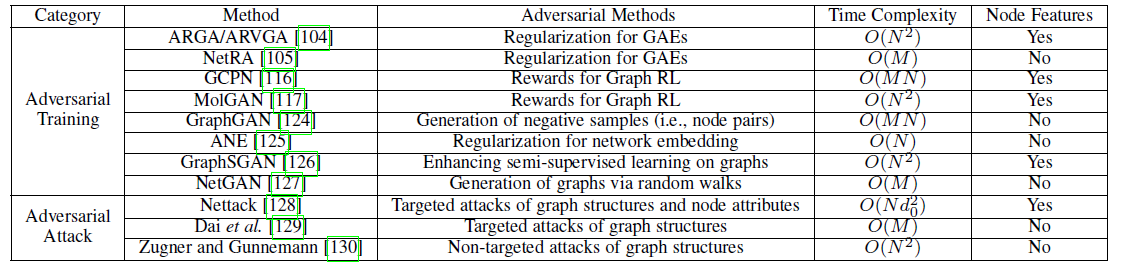
1.6.1 对抗训练
GAN的基本思想是建立两个相关联的模型:判别器discriminator和生成器generator。- 生成器的目标是通过生成假数据来 ”欺骗“ 判别器。
- 判别器的目标是区分样本是来自于真实数据还是由生成器生成的。
然后,两个模型通过使用
minmax game进行联合训练而彼此受益。对抗训练已被证明在生成模型中有效,并提高了判别模型的泛化能力。在前文中,我们分别回顾了如何在
GAE和Graph RL中使用对抗训练方案,这里我们详细回顾了图上的其它几种对抗训练Adversarial Training方法。GraphGAN提出使用GAN来提升具有以下目标函数的graph embedding方法:其中:
判别器
embedding向量。生成器
embedding向量。
结合以上等式,判别器实际上有两个目标:原始图中的节点
pair对应该具有较大的相似性,生成器生成的节点pair对应该具有较小的相似性。该架构和
graph embedding方法(如LINE)相似,除了negative node pair是由生成器作者表明,该方法提升了节点
embedding向量的inference能力。Adversarial network embedding:ANE也采用对抗训练方案来改进网络embedding方法。类似
ARGA,ANE将GAN作为现有网络embedding方法(如DeepWalk)的额外正则化项,通过将先验分布作为真实数据real data并将embedding向量视为生成样本。GraphSGAN使用GAN来提升图的半监督学习。具体而言,作者观察到:应该在子图之间的稠密间隙density gap中生成伪节点,从而削弱现有模型在不同cluster之间的传播效果。为实现该模型,作者设计了一个新的优化目标,该目标具有精心设计的损失项,从而确保生成器在稠密间隙中生成样本。
NetGAN为图生成任务采用了GAN。具体而言,作者将图生成视为一个学习有偏随机游走分布的任务,并采用GAN框架使用LSTM来生成和区分这些随机游走序列。实验表明,使用随机游走也可以学习全局网络模式。
1.6.2 对抗攻击
对抗攻击
Adversarial attack是另一类对抗方法,旨在通过向数据添加较小的扰动来故意 “欺骗“ 目标方法。研究对抗攻击可以加深我们对现有模型的理解,并启发更强大的体系结构。
Nettack是首次提出通过修改图结构和节点属性来攻击节点分类模型(如GCN)的方法。假设目标节点为
其中:
attack约束定义的空间。
简而言之,优化的目标是在图结构和节点属性中找到最佳的合法修改,使得
causative,即攻击是在训练目标模型之前发生的。作者还提出一些针对攻击的约束条件,最重要的约束条件是:攻击应该是 ”微小的“, 即应该仅仅进行很小的修改。具体而言,作者提出保留诸如节点
degree分布和特征共现之类的数据特点。作者还提出了两种攻击方式:直接攻击
direct attack(直接攻击influence attack(仅攻击其它节点),并提出了几种放宽措施以便优化过程易于处理。同一时期,
《Adversarial attack on graph structured data》研究了类似于Nettack的目标函数。但是,他们关注仅更改图结构的情况。他们并没有假设攻击者拥有所有信息,而是考虑了几种情况,每种情况提供了不同数量的信息。最有效的策略
RL-S2V采用structure2vec来学习节点和图的representation,并使用强化学习来解决优化问题。实验结果表明,这些攻击对于节点和图分类任务均有效。前面提到的两种攻击都是针对性的,即它们旨在引起某些目标节点
《Adversarial attacks on graph neural networks via meta learning》率先研究了非目标攻击,这些攻击旨在降低整体模型的性能。他们将图结构视为要优化的超参数,并在优化过程中采用了元梯度
meta-gradient,同时还采用了几种逼近元梯度的技术。
1.7 讨论和总结
应用:除了诸如节点分类、图分类之类的标准的图
inference任务之外,基于图的深度学习方法也应用于多种学科,包括建模社会影响力、推荐、化学和生物学等等。由于这些应用多种多样,对其进行彻底的回顾超出了本文的范围,但是我们列出了一些关键的灵感:首先,在构建图或者选择架构时,将领域知识纳入模型非常重要。
例如,基于
relative distance构建的图可能适用于交通预测问题,但可能不适用于地理位置也很重要的天气预报问题。其次,基于图的模型通常可以在其它体系结构之上构建,而不是作为独立模型构建。如
例如,计算机视觉社区通常采用
CNN来检测对象,然后将基于图的深度学习用作推理模块。
这些应用还表明:基于图的深度学习不仅可以挖掘现有图数据背后的丰富价值,还有助于将关系型数据自然地建模为图,从而极大地扩展了基于图的深度学习模型的适用性。
未来方向:
新模型用于未研究过的图结构:由于图数据的结构各种各样,因此现有方法不适合所有图结构。
例如,大多数方法集中于同质图,很少研究异质图。
现有模型的组合:可以集成很多现有架构,如将
GCN用作GAE或Graph RL中的一层。除了设计新的构建
block之外,如何系统性地组合这些体系结构也是未来一个有趣的方向。动态图:现有大多数方法都关注于静态图,而实际上很多图本质上是动态的,图的节点、边、特征都可以随时间变化。
例如社交网络中,人们可能建立新的社交关系、删除旧的社交关系,并且他们的特征(如兴趣爱好职业)会随着时间改变。新用户可以加入社交网络、现有用户也可以离开。
如何对动态图的不断变化的特点进行建模,以及如何支持对模型参数的增量更新仍是悬而未决的。
可解释性和鲁棒性:由于图通常和其它风险敏感
risk-sensitive的场景相关,因此深度学习模型结果的可解释能力对于决策问题至关重要。例如,在医学或与疾病相关的问题中,可解释性对于将计算机实验转化为临床应用至关重要。
但是,基于图的深度学习的可解释性甚至比其它黑盒模型更具挑战性,因为图的节点和边通常紧密相连。
此外,正如对抗攻击所示,许多现有的图深度学习模型对于对抗攻击都很敏感,因此提升现有方法的鲁棒性是另一个重要问题。
二、GNN : A Review of Methods and Applications[2018]
摘要:很多学习任务需要处理包含元素之间丰富的关系信息的图数据。图神经网络
Graph Neural Networks:GNNs是连接主义的模型connectionist model,它通过图上节点之间的消息传递来捕获图的依赖关系。与标准的神经网络不同,图神经网络保留了一个状态,该状态能够代表来自任意深度的邻域的信息。尽管发现原始GNN难以训练得到一个不动点fixed point,但是网络体系结构、优化技术、并行计算的很多最新进展使得图神经网络能够成功地学习。近年来基于图神经网络的变体,如图卷积神经网络
Graph Convolutional Network: GCN、图注意力网络Graph Attention Network: GAT、图门控神经网络gated graph neural network: GGNN已经在很多任务上展现了突破性的性能。引言:图
Graph是一种数据结构,可用于一组对象(节点)及其关系(边)进行建模。近年来,由于图的强大表示能力,图的分析和研究受到越来越多的关注。作为机器学习中唯一的非欧几何数据结构,图分析重点关注于节点分类、链接预测、聚类。图神经网络Graph Neural Networks: GNN是在图上执行的、基于深度学习的方法。由于GNN令人信服的性能和高解释性,GNN最近已经成为一种广泛应用的图分析方法。采用
GNN有以下的动机motivation:GNN第一个动机源于卷积神经网络CNN。CNN可以提取多尺度局部空间特征,并将其组合以构建高度表达能力的representation。这导致了几乎所有机器学习领域的突破,并开启了深度学习的新时代。随着我们对
CNN和图的深入研究,我们发现CNN的关键特性:局部链接、权重共享、使用multi-layer。这些对于解决图领域的问题也非常重要,因为:- 图是最典型的局部连接结构。
- 和传统的谱图理论
spectral graph theory相比,共享权重降低了计算成本。 multi-layer结构是处理层级模式hierarchical pattern的关键,它捕获了各种尺度的特征。
但是,
CNN只能处理诸如图像(2D网格)、文本(1D序列)之类的常规欧氏空间的数据。一种直觉的想法是将CNN推广到图数据上。然而,很难在图上定义局部卷积操作和池化操作,这阻碍了CNN应用到非欧空间的图上。GNN第二个动机来自于graph embedding。graph embedding学习图的节点、边或者子图subgraph的representatation低维向量。在图分析领域,传统机器学习方法通常依赖于人工设计的特征,这种方式灵活性较差、成本很高。 结合表示学习
representation learning思想以及word embedding的做法,DeepWalk是第一种基于表示学习的graph embedding方法,它将SkipGram模型应用于图上生成的随机游走序列。类似的方法,如node2vec,LINE, TADW也取得了突破。但是,这些方法有两个严重不足:
- 首先,编码器中的节点之间没有共享参数,这导致计算效率较低。因为这意味着参数数量随着节点数量线性增加。
- 其次,直接
embedding的方法缺少泛化能力,这意味着它们无法处理动态图,也无法泛化到新的图上。
基于
CNN和graph embedding,人们提出了GNN来聚合图结构中的信息,从而可以对节点及其关联进行建模。论文
《Graph Neural Networks: A Review of Methods and Applications》对现有的图神经网络模型进行详细的综述,并解释了GNN值得研究的根本原因:首先,像
CNN/RNN这样的标准神经网络无法正确处理图输入,因为它们按照特定顺序堆叠了节点特征。但是,图的节点没有自然顺序natural order。为了解决这个问题,GNN分别在每个节点上传播,从而忽略了节点的输入顺序。即:GNN的输出对于节点的输入顺序是不变的。其次,图的边表示两个节点的依赖关系。在标准神经网络中,依赖关系仅被视为节点的特征。但是,
GNN可以通过图结构进行传播,而不必将其用作特征的一部分。第三,推理
reasoning是高级人工智能的一个非常重要的研究课题,人脑的推理过程几乎是基于从日常经验中提取的图。标准的神经网络已经显示出通过学习数据的分布来生成合成的synthetic图像和文档的能力,但是它们仍然无法从大型数据中学习reasoning graph。而
GNN试图从诸如场景图片、故事文档之类的非结构化数据生成graph,这可以作为进一步的高级人工智能的强大神经网络模型。最近,已经证明具有简单架构的、未经训练的
GNN也可以很好地发挥作用。
论文贡献:
- 论文对现有的图神经网络模型进行了详细的回顾。作者介绍了原始模型、变体、以及若干个通用框架。作者研究了这一领域的各种模型,并提供了一个
unified representation来展示不同模型中的不同propagation步骤。通过识别相应的aggregator和updater,人们可以很容易地区分不同的模型。 - 论文对应用进行了系统的分类,将应用分为结构性场景、非结构性场景和其他场景。在每个场景下,论文提出了几个主要的应用和相应方法。
- 论文提出了未来研究的四个开放性问题。图神经网络存在
over-smoothing和scaling问题。目前还没有有效的方法来处理动态图以及非结构化的感官数据non-structural sensory data的建模。作者对每个问题进行了深入分析,并提出了未来的研究方向。
2.1 模型
2.1.1 GNN
GNN的概念第一次是在论文《The graph neural network model》中被提出,它用于处理图数据并扩展了现有的神经网络。GNN的目标是:对于每个节点state embedding向量embedding进一步地可以用于产生节点label。其中embedding维度,GNN定义了两个函数:- 定义
local transition function。它在所有节点之间共享,并根据每个节点的输入特征和邻域来更新节点状态向量。 - 定义
local output function。它也在所有节点之间共享,并根据每个节点的状态向量来计算节点输出。
其中函数
根据这两个函数,则
GNN的更新方程为:其中:
- 定义
令
其中:
global transition function,它是考虑图上所有节点的global output function,它是考虑图上所有节点的
实际上
contraction map才有定义。基于
Banach不动点理论,GNN使用以下经典的迭代方案来计算状态矩阵:其中
当得到
GNN框架时,下一个问题是如何学习基于监督信息,损失函数可以为:
其中:
one-hot之后的向量。
然后我们基于梯度下降法按照以下步骤来进行学习:
通过公式
然后从损失函数中计算权重
根据梯度来更新权重
尽管实验结果表明
GNN是用于对图结构数据建模的强大工具,但是原始GNN仍然存在一些局限性:- 首先,迭代不动点从而更新节点状态的效率太低。如果放松不动点的假设,则我们可以设计一个多层
GNN来获得节点及其邻域的stable representation。 - 其次,
GNN在迭代 不动点过程中使用相同的参数。但是,流行的神经网络在不同的layer使用不同的参数,这是一种层次hierarchical特征提取方法。 - 第三,边上存在一些信息特征,这些特征无法在原始
GNN中有效建模。例如,异质图中包含不同类型的边,那么不同类型边的消息传播应该有所不同。 - 最后,如果我们专注于节点的
representation而不是图的representation,则不动点并不合适。因为不动点的representation分布过于平滑,使得难以很好地区分不同的节点。
- 首先,迭代不动点从而更新节点状态的效率太低。如果放松不动点的假设,则我们可以设计一个多层
2.1.2 GNN 变体
GNN的变体有三类:基于图类型的变体Graph Types、基于传播步骤的变体Propagation Step、基于训练方法的变体Training Methods。下图概括了这三类变体。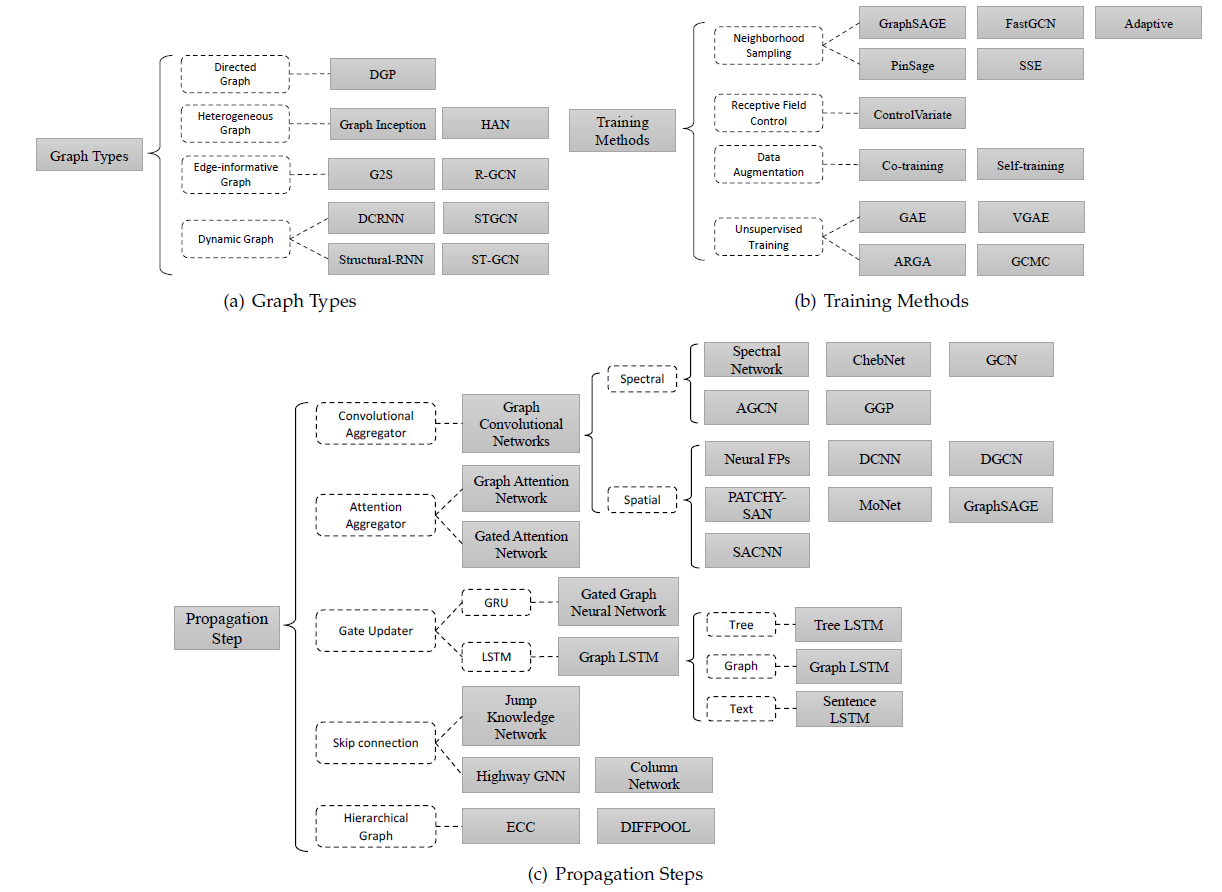
a. Graph Types
原始
GNN中,输入图由带标签信息的节点以及无向边组成,这是最简单的图。下面我们介绍针对不同类型的图进行建模的方法。有向图:有向边相比无向边可以带来更多的信息。在知识图谱中,边从
head entity指向tail entity,表示head entity是tail entity的父节点。这表明我们应该区别对待head entity(父节点)和tail entity(子结点)。DGP(《Rethinking knowledge graph propagation for zero-shot learning》)使用两种权重矩阵其中:
representation矩阵。sigmoid函数。其中
异质图:异质图存在多种类型的节点。
- 处理异质图最简单的方法是将节点类型转换为
one-hot向量,然后拼接这个one-hot向量到节点原始特征向量之后作为节点新的特征向量。 - 此外,
GraphInception将metapath的概念引入到异质图传播过程中。通过metapath,我们可以根据邻居节点的类型、邻居节点距当前节点的距离来对邻居节点进行分组。对于每个分组,GraphInception将其视为同质图中的子图进行传播,并将不同分组的传播结果拼接起来作为邻域节点集合的representation。 - 最近,
heterogeneous graph attention network: HAT提出利用node-level注意力和semantic-level注意力来同时考虑节点重要性和meta-path重要性。
- 处理异质图最简单的方法是将节点类型转换为
边信息:在图的另一类变体中,每条边都带有边信息,如边的权重或类型。对于带边信息的图,有两种处理方式:
首先,可以将图转换为二部图,其中原始边变成节点(称作
edge node),并且一条原始边被拆分为两条新边。这意味着edge node分别和原始边的开始节点、结束节点都存在连接。其次,我们可以对不同类型的边上的传播使用不同的权重矩阵。在
G2S(《Graph-to-sequence learning using gated graph neural networks》) 中,encoder使用如下的聚合函数:其中:
representation向量。reset gate。
当边的类型非常多时,
R-GCN引入了两种正则化来减少关系建模的参数数量:基分解basis-decomposition、块对角分解block-diagonal-decomposition。对于基分解,每个
其中每个
basis transformation对于块对角分解,
R-GCN通过一组低维矩阵直接求和来定义每个
动态图:动态图具有静态图结构和动态输入信号。
- 为捕获这两种信息,
DCRNN和STGCN首先通过GNN收集空间信息spatial information,然后将输出馈送到序列模型(如sequence-to-sequence或者CNN) 从而捕获时序信息temporal information。 - 不同的是,
Structure-RNN和ST-GCN同时收集空间信息和时序信息。它们通过时序连接temporal connnection扩展了静态图结构,因此可以在扩展图上应用传统的GNN。
- 为捕获这两种信息,
b. Propagation Step
在模型中,
propagation step和output step对于获取节点(或边)的representation至关重要。对于output step而言,通常都采用和原始GNN相同的、简单的前馈神经网络。但是对于propagation step,已经有很多种不同于原始GNN的修改,如下表所示。这些变体利用不同的聚合器
aggregator从每个节点的邻域聚合消息,并使用不同的更新器updater来更新节点的hidden state。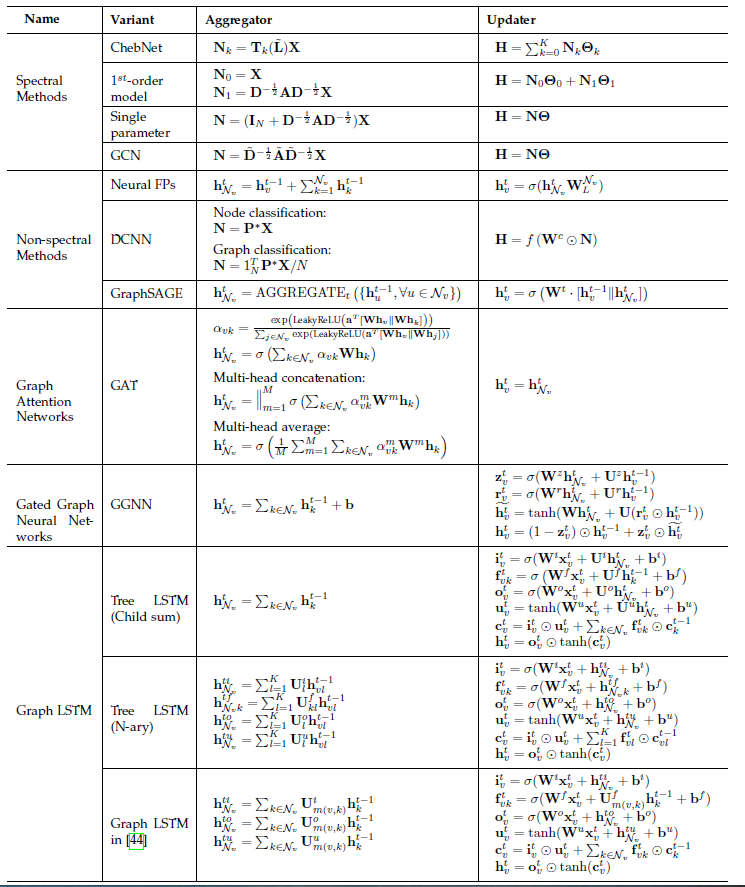
Convolution:近期卷积被应用到图领域,其中主要分为谱域卷积spectral convolution和空间卷积spatial convolution。谱域卷积使用图的谱域表示:
Spectral Network:论文
《Spectral networks and locally connected networks on graphs》提出了谱域网络spectral network。它通过对图的拉普拉斯算子执行特征分解eigendecomposition,从而在傅里叶域Fourier domain定义卷积运算。定义图卷积算子
其中:
eigenvector组成的矩阵 。- 图拉普拉斯矩阵
定义谱域卷积核为
eigenvalue因此作用在输入信号
其中
这种卷积操作的计算复杂度太高,并且得到的滤波器是非空间局部化的
non-spatially localized。因此,《Deep convolutional networks on graph-structured data》试图通过引入具有平滑系数的参数来使得谱域滤波器在空域是局部化的。ChebNet:《Wavelets on graphs via spectral graph theory》提出其中:
根据切比雪夫多项式的递归定义,有:
因此有:
可以看出该卷积操作是拉普拉斯矩阵的
K阶局部化的K-localized。《Convolutional neural networks on graphs with fast localized spectral filtering》提出了ChebNet,它利用这种K-localized卷积运算来定义卷积神经网络,从而避免计算拉普拉斯矩阵的特征向量eigenvector。GCN:《Semi-supervised classification with graph convolutional networks》通过限制K=1,从而缓解在节点degree分布范围非常广的图中局部邻域结构上的过拟合问题。进一步地它假设其中包含两个参数
为减少参数数量并令
注意,堆叠该卷积算子可能会导致数值不稳定性以及梯度消失、梯度爆炸。因此,
GCN引入renormalization技巧:其中
最终,
GCN将上述卷积算子推广到信号其中:
这里的输入通道数量
上述所有方法均使用原始图结构来表明节点之间的关系,然而不同节点之间可能存在隐式关系。为此,
《Adaptive graph convolutional neural networks》提出了Adaptive Graph Convolution Network:AGCN来学习潜在关系。AGCN学习一个残差residual图的拉普拉斯算子,并将该残差图的拉普拉斯算子添加到原始的图拉普拉斯算子中。结果在多个图数据集中证明了AGCN的有效性。另外
《Bayesian semi-supervised learning with graph gaussian processes》提出了一种基于高斯过程的贝叶斯方法Gaussian process-based Bayesian approach:GGP来解决半监督学习问题。它展示了GGP和谱域卷积方法之间的相似之处,这可能会从另一个角度为我们提供一些洞察。
但是,上述所有谱域方法中,学习的滤波器都取决于拉普拉斯矩阵的特征根
eigenbasis,而拉普拉斯特征根取决于图结构。即,在特定结构的图上训练的模型无法直接应用于具有不同结构的其它图上。空域卷积直接在图上定义卷积,并在空间上相邻的邻域上进行计算。空域方法的主要挑战是:为具有不同大小邻域的节点定义卷积运算,并保持
CNN的局部不变性。Neural FPs:《Convolutional networks on graphs for learning molecular fingerprints》对不同degree的节点使用不同的权重矩阵:其中
degree为该方法的主要缺点是无法应用于节点
degree范围很广的大型图。DCNN:《Diffusion-convolutional neural networks》提出diffusion-convolutional neural networks: DCNN,它利用转移矩阵来定义节点邻域。对于节点分类问题,有:其中:
F为节点特征向量的维度。diffusion representation。
对于图分类任务,
DCNN简单地将节点的representation取平均:其中
1的向量。DCNN也可以用于边分类任务,只需要将边转换为节点并调整邻接矩阵即可。DGCN:《Dual graph convolutional networks for graph-based semi-supervised classification》提出了dual graph convolutional network:DGCN来同时考虑图的局部一致性和全局一致性。它使用两个卷积网络来捕获局部一致性和全局一致性,并采用无监督损失来集成ensemble它们。第一个卷积网络和
GCN相同:第二个卷积网络使用
positive pointwise mutual information:PPMI矩阵代替邻接矩阵:其中:
PPMI矩阵,degree矩阵。
PATCHY-SAN:PATCHY-SAN模型为每个节点提取并归一化邻域,其中邻域刚好包含receptive field。LGCN:LGCN利用CNN作为聚合器。它对节点的邻域矩阵进行最大池化,并获取top-k个特征,然后应用一维卷积来计算hidden representation。MoNet:MoNet推广了前面的几种技术。在流形manifold上的Geodesic CNN:GCNN和Anisotropic CNN:ACNN、在图上的GCN,DCNN都可以视为MoNet的特例。GraphSAGE:GraphSAGE提出了一个通用的inductive框架,它通过对节点的局部邻域特征进行采样和聚合来生成节点embedding:其中
但是,
GraphSAGE并没有使用节点邻域中的所有节点来计算GraphSAGE采用了三种聚合函数:均值聚合:
均值聚合和其它两种聚合不同,因为它并没有将
skip connection的一种形式,并可以实现更好的性能。LSTM聚合:AGG使用表达能力很强的LSTM网络。但是,LSTM处理序列数据,因此并不是排列不变的permutation invariant。LSTM通过对节点邻域随机排序从而应用于无序的邻域集合。池化聚合:
AGG使用最大池化:.
Gate:有一些工作试图在传播step中引入门控机制(类似于GRU/LSTM),从而减少之前GNN模型中的缺陷,并改善信息在整个图结构中的long-term传播。GGNN:《Gated graph sequence neural networks》提出了gated graph neural network:GGNN,它在传播阶段使用Gate Recurrent Units:GRU,展开unroll固定的T个递归步并通过backpropagation through time:BPTT计算梯度。具体而言,传播模型的基本递归
basic recurrence公式为:其中:
update gate,reset gate。节点
GRU的更新函数结合了来自其它节点的信息和上一个时间步的信息,从而更新每个节点的hidden state。Tree-LSTM:在基于树或图的传播过程中,
LSTM也以GRU相似的方式使用。《Improved semantic representations from tree-structured long short-term memory networks》提出基于LSTM的两个扩展:Child-Sum Tree-LSTM和N-ary Tree-LSTM。类似于标准的
LSTM单元,每个Tree-LSTM单元(由input gateoutput gatememmory cellhidden stateTree-LSTM单元对于每个childforget gatechild的信息。Child-Sum Tree-LSTM递归方程如下:其中
LSTM中时刻这里的
LSTM作用的是节点的状态序列,而GraphSAGE中的LSTM作用的是节点的邻域。如果树的分支因子最多为
1,...,K进行索引,则可以使用N-ary Tree-LSTM。对于节点
chid在时刻hidden state和memory cell。N-ary Tree-LSTM的递归方程如下:和
Child-Sum Tree-LSTM相比,N-ary Tree-LSTM为每个childchild的细粒度表示。这两种类型的
Tree-LSTM可以轻松地应用于图。
Graph LSTM:《Conversation modeling on reddit using a graph-structured lstm》中的graph-structured LSTM是N-ary Tree-LSTM应用于图上的例子。但是它是简化版本,因为图中的每个节点最多具有
2个入边incoming edge(从它的父亲parent以及同辈的前驱sibling predecessor)。《Cross-sentence n-ary relation extraction with graph lstms》基于关系抽取任务提出了Graph LSTM的另一种变体。图和树之间的主要区别在于图的边具有标签
label,因此该论文使用不同的权重矩阵来表示不同label的边:其中
edge label。《Sentence-state lstm for text representation》提出了用于改进text encoding的Sentence LSTM:S-LSTM。它将文本转换为图,并利用Graph LSTM来学习representation。S-LSTM在很多NLP问题中展现出强大的表示能力。《Semantic object parsing with graph lstm》提出了一种Graph LSTM网络来解决语义对象解析任务semantic object parsing task。它使用置信度驱动方案confidence-driven scheme来自适应地选择开始节点并决定节点更新顺序。它遵循相同的思想来推广LSTM到图结构数据上,但是具有特定的更新顺序。而我们上述提到的方法和节点的顺序无关。
Attention:注意力机制已经成功地应用于很多sequence-based任务,例如机器翻译、机器阅读等。《Graph attention networks》提出了graph attention network: GAT从而将注意力机制融合到传播步骤。它采用self-attention机制,通过关注节点的邻域来计算节点的hidden state。GAT定义一个graph attention layer,并通过堆叠多个graph attention layer来构建graph attention network。该层通过以下方式计算节点pair对其中:
graph attention layer的输入为节点的特征集合graph attention layer的输出为节点的新的特征集合feedforward neural network的权重。attention系数。它满足:
此外,
GAT利用multi-head attention来稳定学习过程。它使用hidden state,然后将这hidden state拼接起来(或均值聚合),从而得到以下两种形式的representation:其中
attention计算到的注意力系数。GAT的注意力架构具有几个特点:- 节点-邻居
pair对的计算是可并行的,因此计算效率很高。 - 通过为邻域指定不同的权重,因此可以应用于不同
degree的节点。 - 可以轻松地应用于
inductive learning。
GANN:除了GAT之外,Gated Attention Network:GAAN也是用multi-head注意力机制。但是,它使用self-attention机制从不同的head收集信息,而不是像GAT那样拼接或者取平均。即每个head的重要性不同。
Skip connection:很多应用application会堆叠多层神经网络从而预期获得更好的结果。因为更多的层,比如可以从计算机视觉社区找到一种直接的解决方案,即残差网络
residual network。但是,即便使用残差连接,在很多数据集上具有多层的GCN的性能也不如2层GCN更好。Highway GCN:《Semi-supervised user geolocation via graph convolutional networks》提出Highway GCN,它使用类似于highway networks的layer-wise gate。layer的输出和layer的输入加权累加,权重由门控给出:通过增加
higthway gate,4层的Higthway GCN在某些特定问题上性能最佳。论文
《Column networks for collective classification》提出的Column Network:CLN也使用highway network,但是它使用不同的函数来计算门控权重。JK-Net:《Representation learning on graphs with jumping knowledge networks》研究了邻域聚合方案的特点以及邻域聚合导致的缺陷。该论文提出了Jump Knowledge Network:JK-Net,它可以学习自适应adaptive的 、结构感知structure-aware的representation`。JK-Net将节点的每一层中间representation跳跃到最后一层,并在最后一层对这些中间representation进行自适应地选择,从而使得模型可以根据需要自适应地调整每个节点的有效邻域大小。JK-Net在实验中使用了三种聚合方式来聚合信息:拼接、最大池化、LSTM-attention。它也可以和Graph Convolutional Network, GraphSAGE, Graph Attention Network等模型结合,从而提升后者的性能。
Hierarchical Pooling:在计算机视觉领域,卷积层之后通常跟着池化层从而获得更加泛化的特征。和视觉领域的池化层相似,有很多工作集中在图上的层次池化层hierarchical pooling layer。复杂的大型图通常带有丰富的层次结构,这对于node-level和graph-level任务非常重要。为了探索这种内部特征
inner features,Edge-Conditioned Convolution:ECC设计了具有递归下采样操作的池化模块。下采样方法通过拉普拉斯矩阵的最大特征向量的符号将图划分为两个分量。DIFFPOOL通过对每一层训练一个assignment矩阵,从而提出了一个可学习的层次聚类模块:其中:
feature矩阵,coarsened adjacency matrix。
c. Training Methods
原始的图卷积神经网络在训练和优化方法上存在缺陷:
- 首先,
GCN需要完整的图拉普拉斯算子,这对于大型图来讲计算量太大。 - 其次,在第
embedding时需要该节点邻域所有节点在第embedding。因此,单个节点的感受野相对于层数呈指数型增长,因此计算单个节点的梯度的代价很大。 - 最后,
GCN针对给定的图训练,这缺乏inductive learning能力。
- 首先,
Sampling:GraphSAGE:GraphSAGE是原始GCN的全面改进。为解决上述问题,GraphSAGE用可学习的聚合函数替换了完整的图拉普拉斯算子,这是执行消息传递和泛化到未见过节点的关键:GraphSAGE首先聚合邻域embedding,然后和目标节点的embedding拼接,最后传播到下一层。通过可学习的邻域聚合函数和消息传播函数,
GraphSAGE可以泛化到未见过的节点。此外,
GraphSAGE使用邻域采样来缓解感受野的扩张expansion。PinSage:PinSage提出了基于重要性的采样方法。通过模拟从目标节点开始的随机游走,该方法选择了归一化访问次数topFastGCN:FastGCN进一步改善了采样算法。FastGCN不会为每个节点采样邻居,而是直接为每层采样整个感受野。FastGCN也使用重要性采样,但是其重要性因子为:和上面固定的采样方法相反,论文
《Adaptive sampling towards fast graph representation learning》引入了一个参数化、且可训练的采样器来执行以前一层为条件的逐层采样。此外,该自适应采样器可以找到最佳采样重要性并同时减少采样方差。SSE:遵循强化学习,论文《Learning steady-states of iterative algorithms over graphs》提出SSE,它采用Stochastic Fixed-Point Gradient Descent用于GNN的训练。该方法将
embedding更新视为值函数value function。在训练期间,该算法将对节点进行采样以更新embedding, 对标记节点采样以更新参数,二者交替进行。
Receptive Field Control:《Stochastic training of graph convolutional networks with variance reduction》通过利用节点的历史激活作为控制变量control variate,提出了一种基于控制变量的GCN随机近似算法。该方法限制了一阶邻域中的感受野,但使用历史hidden state从而作为一个可接受的近似值。Data Augmentation:《Deeper insights into graph convolutional networks for semi-supervised learning》聚焦于GCN的局限性,其中包括GCN需要许多额外的标记数据用于验证集,并且还遭受卷积滤波器的局部性。为解决这些限制,作者提出了Co-Training GCN以及Self-Training GCN来扩大训练集。前者寻找训练标记样本的最近邻居,后者遵循类似boosting的方法。Unsupervised training:GNN通常用于监督学习或半监督学习,最近有一种趋势是将自编码器auto-encoder:AE扩展到图领域。图自编码器旨在通过无监督学习获取节点的低维representation。GAE:论文
《Variational graph auto-encoders》提出了Graph Auto-Encoder: GAE。GAE是首次使用GCN对图中的节点进行编码,然后它使用简单的解码器重构邻接矩阵,并根据原始邻接矩阵和重构邻接矩阵之间的相似度来评估损失:论文也以变分的方式训练
GAE模型,称作变分图自编码器variational graph autoencoder:VGAE。此外,
graph convolutional matrix completion:GC-MC也使用GAE并应用于推荐系统中。在MovieLens数据集上,GC-MC性能优于其它baseline模型。ARGA:Adversarially Regularized Graph Auto-encoder:ARGA使用生成对抗网络generative adversarial network:GAN来正则化GCN-based的GAE从而遵循先验分布。也有几种图自编码器,例如
NetRA, DNGR, SDNE, DRNE,但是它们的架构中未使用GNN。
2.2 通用框架
除了图神经网络的不同变体之外,人们还提出了一些通用框架,旨在将不同的模型整合到一个框架中。
《Neural message passing for quantum chemistry》提出了消息传递神经网络message passing neural network: MPNN,它统一了各种图神经网络和图卷积网络方法。《Non-local neural networks》提出了非局部神经网络non-local neural network: NLNN,它统一了集中self-attention风格的方法。《Relational inductive biases, deep learning, and graph networks》提出了一种图网络graph network: GN,它统一了MPNN、NLNN以及许多其它变体,例如Interaction Network、Neural Physics Engine、CommNet、structure2ve、GGNN、Relation Network、Deep Sets、Point Net。
2.2.1 MPNN
MPNN框架总结了几种最流行的图模型之间的共性,如graph convolution network, gated graph neural network, interaction network, molecular graph convolution, deep tensor neural network等等。MPNN包含两个阶段:消息传递阶段、readout阶段 。消息传递阶段(也称作传播阶段)执行
令节点
hidden state为其中
readout阶段使用Readout函数其中
T表示总的时间步。
消息函数
readout函数MPNN框架可以通过不同的配置来概括几种不同的模型。这里我们以
GGNN为例,其它模型的示例参考原始论文。针对GGNN模型的函数配置为:其中:
edge label采用不同的邻接矩阵。GRU为Gated Recurrent Unit。
2.2.2 NLNN
NLNN用户捕获深度神经网络的长程依赖。non-local操作是计算机视觉中经典的non-local均值操作的推广。non-local操作将某个位置的response计算为所有位置的特征的加权和,位置可以为空间位置、时间位置、或者时空位置。因此,NLNN可以视为不同的self-attention方式的统一。我们首先介绍
non-local操作的一般定义。遵从non-local均值操作,推广的non-local操作定义为:其中:
有几种不同的
NLNN使用线性变换作为高斯
Gaussian函数:高斯函数是根据非局部均值non-local mean(论文《A non-local algorithm for image denoising》)和双边滤波器bilateral filter(论文《Bilateral filtering for gray and color images》)的自然选择:其中,
dot-product similarity。并且:Embedded Gaussian函数:很自然地通过计算embedding空间中的相似性来扩展高斯函数。即:其中:
可以发现
《Attention is all you need》提出的self-attention是Embedded Gaussian函数的特例。对于给定的softmax。因此有:这就是
self-attention的形式。点积函数:
dot-product similarity,即:其中:
其中
拼接函数:
其中:
NLNN将上述non-local操作包装到一个non-local block中:其中
non-local block可以插入任何预训练模型pre-trained model中,这使得该block适用性更好。
2.2.3 GN
Graph Network:GN框架概括并扩展了各种图神经网络、MPNN、以及NLNN方法。我们首先介绍图的定义,然后描述GN块、GN核心计算单元、计算步骤。在
GN框架内,图被定义为三元组receiver节点,sender节点。
一个
GN块包含三个更新函数其中:
其物理意义为:
sender节点属性receiver节点属性receiver为当前节点的所有边的属性(更新后的边属性)的聚合值- 每个
permutation invariant,并且应该采用可变数量的自变量。一些典型的例子包括:逐元素求和、均值池化、最大值池化等。
GN块的计算步骤:通过执行
- 更新后,边的集合为
- 更新后,节点
receiver。
- 更新后,边的集合为
执行
通过执行
更新后,所有节点的属性集合为
通过执行
通过执行
通过执行
尽管这里我们给出了计算步骤的顺序,但是并不是严格地根据这个顺序来执行。例如,可以先更新全局属性、再更新节点属性、最后更新边属性。
设计原则:
Graph Network的设计基于三个基本原则:灵活的representation、可配置的块内结构within-block structure、可组合的多块架构multi-block architecture。灵活的
representation:GN框架支持属性的灵活representation,以及不同的graph结构。- 全局属性、节点属性和边属性可以使用任意的表示格式,但实值向量和张量是最常见的。
- 就
graph结构而言,GN框架既可以应用于图结构明确的结构性场景,也可以应用于需要推断关系结构relational structure的非结构性场景。
可配置的块内结构:一个
GN块内的函数及其输入可以有不同的设置,因此GN框架在块内结构配置方面提供了灵活性。基于不同的结构和函数设置,各种模型(如MPNN、NLNN和其他变体)都可以由GN框架表达。可组合的多块架构:
GN块可以被组合从而构建复杂的架构。任意数量的GN块可以用共享参数或不共享参数的方式来堆叠式地组合。也可以采用一些其他技术来构建GN-based架构,如skip connection、LSTM-style门控机制、GRU-style门控机制,等等。
2.3 应用
图神经网络已经在监督学习、半监督学习、无监督学习、强化学习等领域广泛应用。这里我们将应用分为三类:
- 数据具有明确关系结构的结构性场景,如物理系统
physical system、分子结构molecular structure、知识图谱knowledge graph。 - 关系结构不明确的非结构性场景,包括图像
image、文本text等。 - 其它应用场景,如生成模型
generative model、组合优化问题combinatorial optimization problem。
下表给出这些场景的一个总结:
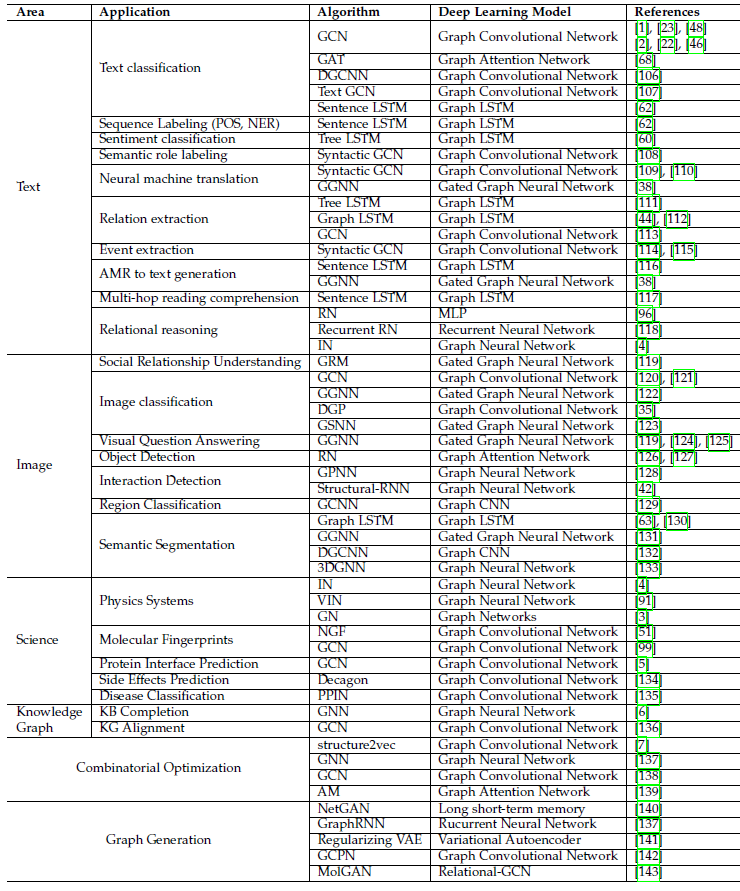
- 数据具有明确关系结构的结构性场景,如物理系统
2.3.1 结构化的场景
物理学:对现实世界的物理系统进行建模是理解人类智能的最基本方面之一。通过将物体表示为节点,将关系表示为边,我们可以用一种简化但有效的方式对物体、关系和物理学进行
GNN-based的推理。分子学和生物学:
- 分子指纹
molecular fingerprint计算:分子指纹是一个代表分子的特征向量,主要用于计算机辅助药物设计。传统的分子指纹是手工制作和固定的,通过将GNN应用于分子图,我们可以获得更好的分子指纹。 - 蛋白质交互预测:蛋白质交互预测任务是一个具有挑战性的问题,在药物发现和设计中有着重要的应用。
- 分子指纹
知识图谱:
《Knowledge transfer for out-of-knowledge-base entities : A graph neural network approach》使用GNN,从而在knowledge base completion: KBC中解决out-of-knowledge-base: OOKB实体问题。《Cross-lingual knowledge graph alignment via graph convolutional networks》使用GCN解决跨语言的知识图谱knowledge graph的对齐问题。
2.3.2 非结构化的场景
图像:
分类任务:几项工作利用图神经网络在图像分类中纳入结构的信息。
- 首先,知识图谱可以作为额外的信息来指导
zero-shot分类。 - 其次, 除了知识图谱之外,数据集中的图像之间的相似性也有助于
few-shot learning。
- 首先,知识图谱可以作为额外的信息来指导
视觉推理任务:计算机视觉系统通常需要通过纳入空间信息和语义信息来进行推理。因此,为推理任务生成
graph是很自然的。一个典型的视觉推理任务是视觉问题回答visual question answering: VQA。视觉推理的其他应用包括目标检测、交互检测和区域分类。语义分割:语义分割任务是为图像中的每一个像素分配一个标签(或类别)。然而,分割区域
region往往不是grid-like并且需要non-local信息,这导致了传统CNN的失败。一些工作利用了图结构数据来处理该任务。
文本:
- 文本分类: 有一些工作把文档或句子看作是一个由
word节点组成的图,还有一些工作依靠文档引用关系来构建图,还有一些工作将文档和词视为构建语料库graph的节点(因此是异质图)。 - 序列标注:由于
GNN中的每个节点都有其隐状态hidden state,如果我们把句子中的每个词都看作是一个节点,我们就可以利用隐状态来解决序列标注问题。 - 神经机器翻译
neural machine translation: NMT:GNN的一个流行应用是将句法信息或语义信息纳入神经机器翻译任务中。
- 文本分类: 有一些工作把文档或句子看作是一个由
2.3.3 其它场景
- 生成式模型:现实世界的图的生成模型因其重要的应用而引起了极大的关注,包括建模社交互动、发现新的化学结构、以及构建知识图谱。由于深度学习方法具有学习图的隐含分布的强大能力,最近神经图生成模型
neural graph generative model出现了一个高潮。 - 组合优化
combinatorial optimization:图上的组合优化问题是一组NP-hard问题,吸引了所有领域的科学家的关注。一些具体的问题,如旅行推销员问题(traveling salesman problem: TSP)和最小生成树(minimum spanning tree: MST),已经得到了各种启发式的解决方案。最近,使用深度神经网络来解决这类问题成为一个热点,其中一些解决方案由于其图结构而进一步利用了图神经网络。
2.4 悬而未决的问题
尽管
GNN在不同领域取得了重大成功,但是GNN仍然还有一些尚未解决的问题:浅层结构
Shallow Structure:传统的深度神经网络可以堆叠数百层从而获得更好的性能,因为更深的结构具有更多的参数从而显著提高表达能力。但是图神经网络总是很浅,大多数不超过三层。实验表明,堆叠多个
GCN层将导致过度平滑,即所有节点都收敛到相同的值。尽管一些研究人员设法解决了该问题,但是它仍然是GNN的最大局限。动态图
Dymaic Graph:另一个挑战是如何处理具有动态结构的图。静态图是稳定的,因此可以对其进行建模。而动态图引入了变化的结构,当边或节点出现或消失时,
GNN无法自适应地调整。非结构化场景
Non-Structural Scenario:没有很好的方法从原始的、非结构的数据生成图结构。如果找到最佳的图构建方法,则可以使得GNN应用范围更广。可扩展性
Scalability:GNN的扩展很困难,因为许多关键步骤在大规模数据下消耗大量的计算资源。例如:- 图数据不是规则的欧几里得结构,每个节点都有自己的邻域结构,因此无法进行
batch处理。 - 当有数百万个节点、边时,计算图拉普拉斯算子是不可行的。
此外,我们必须指出:可扩展性决定了算法能否应用于实际工作中。
- 图数据不是规则的欧几里得结构,每个节点都有自己的邻域结构,因此无法进行
三、A Comprehensive Survey On GNN[2019]
最近神经网络的成功推动了模式识别和数据挖掘的发展。很多机器学习任务,如目标检测、机器翻译、语音识别任务,它们曾经高度依赖于手工特征工程
handcrafted feature engineering来抽取特征,但是这些任务最近被各种端到端的深度学习范式所变革,如卷积神经网络CNN、递归神经网络RNN、自编码器autoencoder。深度学习在许多领域的成功部分归因于快速发展的计算资源(如
GPU)、大量可用的训练数据、以及深度学习从欧几里得数据(如图像、文本、视频)中抽取潜在representation的有效性。以图像数据为例,我们可以将图像表示为欧几里得空间中的规则网格,而卷积神经网络CNN能够利用图像数据的平移不变性shift-invariance、局部连通性local connectivity、以及组合性compositionality。结果,CNN可以抽取在整个数据集上共享的、局部的、有意义的特征,从而进行各种图像分析。虽然深度学习有效地捕获了欧几里得数据的隐藏模式,但是越来越多的应用
application以图graph的形式表示数据。例如:电商领域中基于图的学习系统可以利用用户和商品之间的交互来提高推荐准确性;化学领域中分子被建模为图,并需要确定其生物活性以进行药物发现。图数据的复杂性对现有的机器学习算法提出了重大挑战:- 由于图可能是不规则的,因此图可能包含可变数量的无序节点。而且,图中的节点可能具有不同数量的邻居,从而导致一些在图像领域很容易实施的重要的操作(如卷积)很难应用于图领域。
- 此外,现有机器学习算法的核心假设是样本彼此独立。该假设在图数据上不再成立,因为图数据中每个节点通过各种类型的链接(如引用、好友、交互)和其它节点相关联。
最近越来越多的人关注将深度学习方法扩展到图数据上。受深度学习的
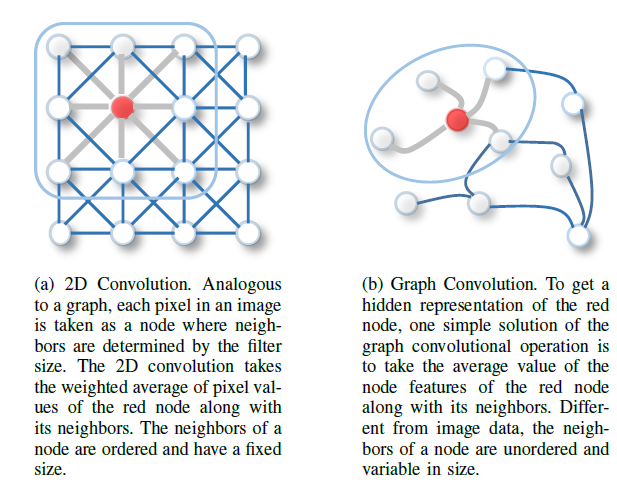
CNN、RNN、autoencoder等技术的推动,过去几年中一些关键算子的新的推广、新的定义快速发展,从而能够处理图数据的复杂性。例如,可以从2D卷积中推广出图卷积。如下图所述,可以将图像视为特殊的、相邻像素连接的图。和2D卷积类似,可以通过获取节点邻域信息的加权均值来执行图卷积。图
(a):一个2D卷积。图像中每个像素视为一个节点,其中邻域由卷积核确定。2D卷积采用红色节点及其邻域像素的像素值的加权平均,节点的邻域是有序的、固定大小的。加权平均的权重由卷积核来指定。
图
(b):一个图卷积。为获得红色节点的hidden representation,一种简单的图卷积运算是获取红色节点及其相邻节点的representation均值。和图像数据不同,节点的邻域是无序的、大小可变的。
目前有关图神经网络
GNN的review的数量有限,论文《A Comprehensive Survey on Graph Neural Networks》给出了一份GNN的全面综述。具体而言:作者提出了新的分类方法,将图神经网络划分为四类:递归图神经网络
recurrent graph neural network:RecGNN、卷积图神经网络convolutional graph neural network:ConvGNN、图自编码器graph autoencoder:GAE、时空图神经网络spatial-temporal graph neural network:STGNN。对于每种类型的图神经网络,作者提供有关代表性模型的详细说明、必要的比较、并总结相应的算法。
作者收集了大量资源,包括
SOTA模型、benchmark数据集、开源代码、实际应用。作者指出:该综述可以用于了解、使用、开发各种现实应用的不同的图深度学习方法的指南hands-on guide。最后作者探讨了图神经网络的理论方面,分析了现有方法的局限性,并就模型深度
model depth、可扩展性scalability、异构性heterogeneity、动态性dynamicity提出了四个未来可能的研究方向。
3.1 背景
GNN的历史:《Supervised neural networks for the classification of structures》首次将神经网络应用于有向无环图,这激励了早期对GNN的研究。《A new model for learning in graph domains》最初概述了图神经网络的概念,《The graph neural network model》进一步阐述了这个概念。这些早期的研究属于递归图神经网络(recurrent graph neural network: RecGNN)的范畴。它们通过以迭代的方式传播邻居信息来学习目标节点的representation,直到达到一个稳定的不动点。这个过程的计算成本很高,最近有越来越多的人在努力克服这些挑战。在计算机视觉领域
CNN成功的鼓舞下,大量为图数据重新定义卷积概念的方法被提出。这些方法都属于卷积图神经网络(convolutional graph neural network: ConvGNN)的范畴。卷积图神经网络分为两个主要方向,即基于谱域的方法和基于空间域的方法。- 第一个关于基于谱域的卷积图神经网络的突出研究是由
《Spectral networks and locally connected networks on graphs》提出的,他们开发了一个基于谱图理论的图卷积。此后,对基于谱域的卷积图神经网络的改进、扩展越来越多。 - 基于空间域的卷积图神经网络的研究比基于谱域开始得更早。
《Neural network for graphs: A contextual constructive approach》首次通过架构上来组合非递归层来解决图的相互依赖性,同时继承了递归图神经网络的消息传递思想。然而,这项工作的重要性被忽略了。
除了递归图神经网络和卷积图神经网络,过去几年中还开发了许多其他的
GNN,包括图自编码器和 "空间-时间"图神经网络。这些学习框架可以建立在递归图神经网络、卷积图神经网络或其他用于图建模的神经架构上。- 第一个关于基于谱域的卷积图神经网络的突出研究是由
GNN vs graph embedding:GNN和graph embedding密切相关。graph embedding目的是将网络节点表示为低维embedding向量,同时保持网络拓扑结构和节点内容信息,以便可以使用简单的、已有的机器学习方法(如支持向量机)轻松执行任何后续的图分析任务(如节点分类、节点聚类、推荐)。GNN是深度学习模型,旨在以端到端的方式解决图相关的任务。很多GNN显式地提取high-level representation。GNN和graph embedding主要区别在于:GNN是一组为各种任务而设计的神经网络模型,而graph embedding覆盖了同一个任务的各种不同方法。因此,GNN可以通过图自编码器框架解决graph embedding问题。- 另一方面,
graph embedding也包含其它非深度学习方法,如矩阵分解MF、随机游走。
GNN vs graph kernel:Graph Kernel曾经是历史上解决图分类问题的主流技术。这些方法设计核函数kernel function来度量graph pair-wise之间的相似度,使得kernel-based算法(如支持向量机)可用于图上的监督学习。- 和
GNN相似,Graph Kernel可以通过映射函数将图或节点嵌入到向量空间。不同之处在于:Graph Kernel的这个映射函数是确定性的,而不是通过学习得到。 - 由于
pair-wise相似性的计算,Graph Kernel方法遇到了计算瓶颈。 GNN基于抽取的graph representation直接执行图分类,因此比Graph Kernel方法更有效。
- 和
3.2 GNN 分类
定义图
- 边
- 节点
- 邻接矩阵
- 每个节点
- 每条边
- 边
定义有向图是所有边都是有向边的图,其中有向边指的是每条边都从一个节点指向另一个节点。
- 无向图是有向图的特殊情况,其中每条有向边都存在与之相反方向的另一条边。
- 当且仅当邻接矩阵是对称矩阵时,图才是无向图。
定义时空图
spatial-temporal graph为一个属性图,其中节点属性随时间动态变化,记作我们将图神经网络
GNN分类为:循环图神经网络RecGNN、卷积图神经网络ConvGNN、图自编码器GAE、时空图神经网络STGNN,如下表所述。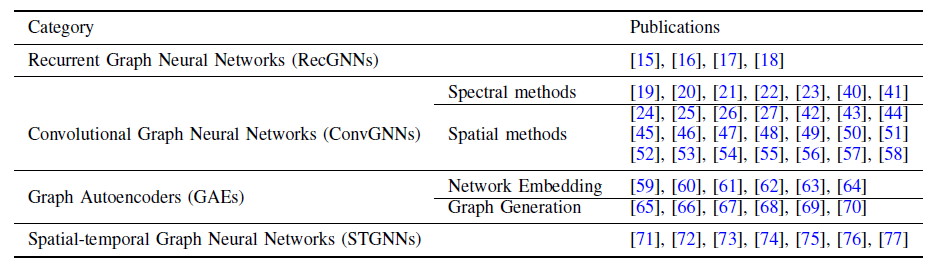
下表给出了各种模型架构的一些示例。
具有多个图卷积层
graph convolutional layer的ConvGNN。图卷积层通过聚合来自邻域的特征信息,从而得到每个节点的hidden representation,并在特征聚合之后再应用非线性变换。通过堆叠多个图卷积层,每个节点的最终hidden representation将接收来自更远邻域的消息。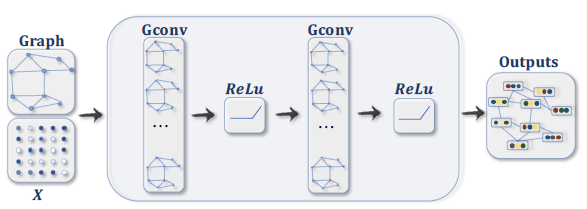
具有池化层和
readout层的、用于图分类的ConvGNN。图卷积层之后是池化层,从而将图粗化coarsen为子图,以便粗化图上的节点representation能够表达更高的graph-level representation。readout层通过获取粗化图所有节点的hidden representation均值或sum结果,从而得到最终的graph representation。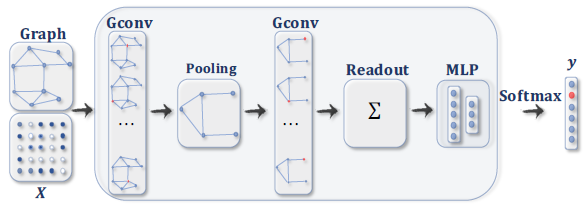
用于
graph embedding的GAE。编码器使用图卷积层获取每个节点的graph embedding,解码器根据graph embedding计算节点的pairwise距离。在应用非线性激活函数之后,解码器重构图邻接矩阵。通过最小化实际的图邻接矩阵、重构的图邻接矩阵之间的差异来训练网络。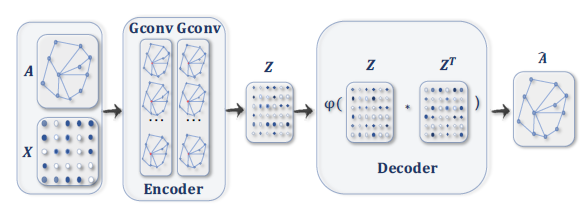
用于时空图预测的
STGNN。图卷积层后面是1D-CNN层:图卷积层在1D-CNN沿时间轴在time step的、未来的取值。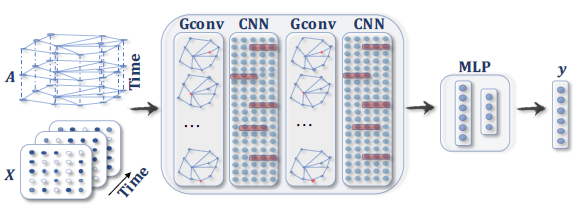
循环图神经网络
RecGNN:大多数是图神经网络的早期作品。RecGNN目的是通过递归神经网络体系架构学习节点的representation。他们假设图中的节点不断与其邻居交换消息,直到到达稳定的平衡。RecGNN在概念上很重要,并激发了后续对卷积图神经网络的研究。具体而言,RecGNN消息传递的思想被基于空间的卷积图神经网络所继承。卷积图神经网络
ConvGNN:推广了从网格数据到图数据的卷积运算。主要思想是通过聚合节点自身的特征representation。和RecGNN不同,ConvGNN堆叠多个图卷积层从而获得high-level节点representation。ConvGNN在搭建很多其它更复杂的GNN模型中起着核心作用。图自编码器
GAE:是一种无监督的学习框架,可以将节点/图编码到潜在的embedding空间,并根据编码后的信息重建图数据。GAE用于学习graph embedding以及图生成分布graph generative distribution。- 对于
graph embedding任务,GAE通过重构图结构信息(如图的邻接矩阵)来学习潜在的节点representation。 - 对于图生成任务,一些方法逐步生成图的节点和边,而另一些方法则一次性生成整个图。
- 对于
时空图神经网络
STGNN:旨在从时空图学习隐藏的模式hidden pattern,这在各种应用中变得越来越重要,例如:交通速度预测traffic speed forecasting、驾驶员操纵预测、人类动作识别等。STGNN的关键思想是同时考虑空间依赖性spatial dependency和时间依赖性temporal dependency。当前的许多方法将图卷积和RNN/CNN集称在一起,其中图卷积捕获空间依赖性,RNN/CNN捕获时间依赖性。GNN的输入为图结构和节点内容信息,但是GNN的输出依赖于具体的图分析任务:node-level输出:和节点回归、节点分类任务有关。RecGNN和ConvGNN可以通过消息传播/图卷积抽取high-level节点representation,然后使用多层感知机multi-perceptron:MLP或者softmax层作为输出层。最终GNN能够以端到端的方式执行node-level任务。edge-level输出:和edge分类、链接预测任务有关。使用来自
GNN的两个节点的hidden representation作为输入,然后利用相似度函数或神经网络来预测边的标签或链接强度。graph-level输出:和图分类任务有关。为获得
graph-level的紧凑表示compact representation,GNN通常与池化操作、readout操作配合使用。
训练框架:可以在端到端学习框架内以监督学习、半监督学习甚至完全无监督学习的方式训练一些
GNN模型(如ConvGNN),具体取决于学习任务和可用的标签信息。用于
node-level分类的半监督学习:给定一个graph其中部分节点带类别标记、剩余节点没有类别标记,ConvGNN可以学习一个robust模型,该模型可以有效地识别未标记节点的类别信息 。为此,可以堆叠几个图卷积层,然后跟一个softmax layer从而构建端到端的多类别分类框架。用于
graph-level分类的监督学习:目的是预测整个图的类标签。可以通过图卷积层、图池化层、和/或readout layer的组合来完成端到端的图分类任务。- 图卷积层负责获取准确的
high-level节点representation。 - 图池化层充当降采样的角色,从而每次都将图粗化
coarsen为子结构sub-structure。 readout layer将图的所有节点压缩为一个graph representation。
通过将一个多层感知机
MLP以及一个softmax layer应用于graph representation,我们可以构建用于图分类的端到端框架。- 图卷积层负责获取准确的
用于
graph embedding的无监督学习:当图没有可用的类标签时,我们可以在端到端框架中以纯无监督的方式学习graph embedding。这些算法以两种方式利用
edge-level信息:- 一种简单的方法是采用自编码器框架,其中编码器使用图卷积层将
graph嵌入到潜在representation空间中,然后对潜在representation应用解码器来重构图结构。 - 另一种流行的方法是利用负采样方法,该方法采样一部分节点
pair对为负边negative edge,而图中具有链接的节点pair对为正边postive edge。然后应用逻辑回归层regression layer来区分正边和负边。
- 一种简单的方法是采用自编码器框架,其中编码器使用图卷积层将
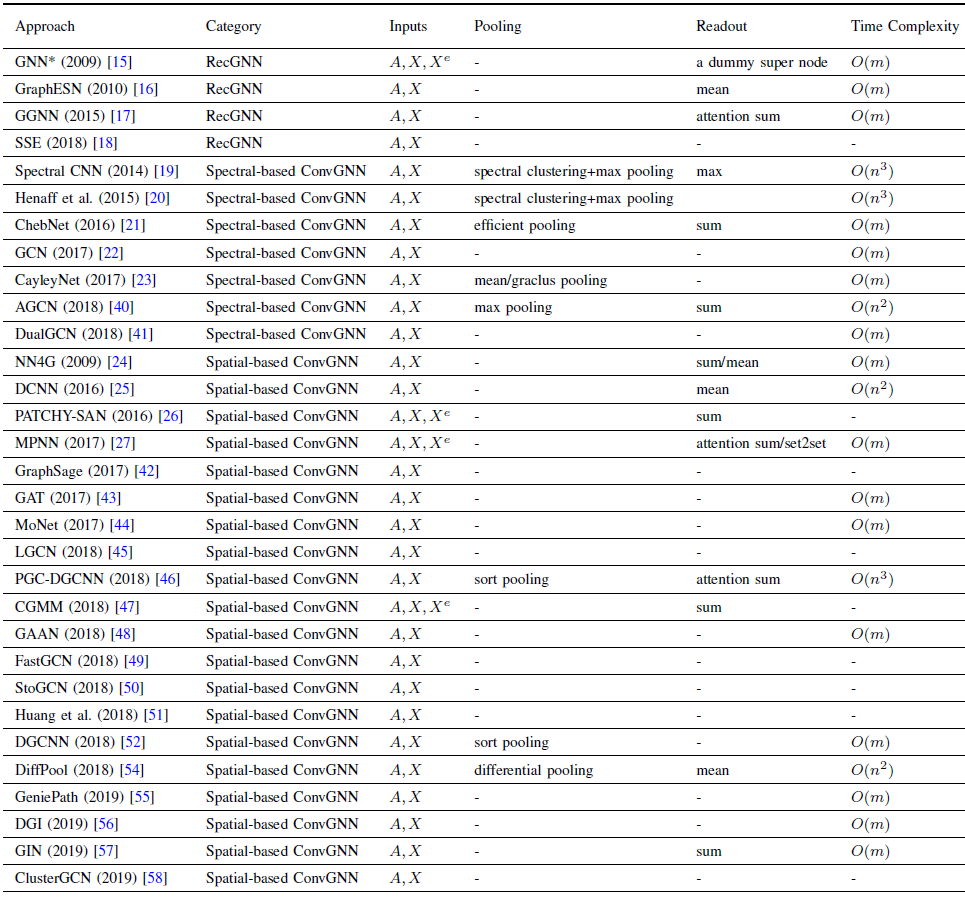
我们在下表中总结了一些典型
RecGNN和ConvGNN的主要特点,并在各种模型之间比较了输入源、池化层、readout layer、以及时间复杂度。更具体而言,我们仅比较每个模型中消息传递/图卷积操作的时间复杂度。由于
《Spectral networks and locally connected networks on graphs》和《Deep convolutional networks on graph-structured data》中的方法需要特征值分解eigenvalue decomposition,因此其时间复杂度为由于需要计算节点
pair对的最短路径,因此《On filter size in graph convolutional networks》的时间复杂度也是其它方法的时间复杂度几乎差不多:如果图的邻接矩阵是稀疏的,则时间复杂度为
这是因为这些方法中,计算每个节点
representation都涉及其degree),并且所有节点上表中缺少几种方法的时间复杂度,这是因为:这些方法在原始论文中缺乏时间复杂度分析,或者仅报告其总体模型或算法的时间复杂度。
池化层和
readout layer中的缺失值-表示该方法仅在node-level/edge-level任务上进行实验。
3.3 RecGNN
RecGNN大多数是GNN的早期研究,它在图上的节点反复应用相同的函数,从而抽取high-level节点representation。受算力的限制,早期研究主要集中于有向无环图上。论文
《The graph neural network model》首次提出了图神经网络GNN,它扩展了已有的递归模型recurrent model从而处理图数据,如带环图、无环图、有向图、无向图等。为区分通用的术语图神经网络,这里我们将论文中的模型记作GNN*。GNN*基于消息传播机制,通过反复交换邻域信息来更新节点的状态,直到达到稳定的平衡状态为止。节点的hidden state反复被更新,更新方程为:其中
hidden state。- 求和运算使得
GNN*适用于所有类型的节点,即使邻居的数量不同并且不知道邻居节点的顺序。 - 为了确保收敛,递归函数
GNN*交替执行节点状态传播、参数梯度计算,从而最小化训练目标。这种策略使得GNN*可以处理有环图。
- 求和运算使得
在后续的工作中,
Graph Echo State Network:GraphESN扩展了echo state network来提升GNN*的训练效率。GraphESN由编码器和输出层组成。其中,fixed node state作为输入来训练输出层。Gated Graph Neural Network:GGNN采用GRU作为递归函数step数量。其优点是:它不再需要约束参数从而确保hidden state根据它之前的hidden state以及邻居的hidden state来更新:其中
与
GNN*、GraphESN不同,GGNN使用时间反向传播back-propagation through time:BPTT算法来学习模型参数。这对于大型图可能会出现问题,因为GGNN需要在所有节点上多次运行递归函数,并要求将所有节点的中间状态存储在内存中。Stochastic Steady-state Embedding:SSE提出了一种学习算法,该算法对大型图更具有可扩展性scalable。SSE以随机的、异步的方式递归地更新节点hidden state。它交替采样一个batch的节点用于状态更新、采样一个batch的节点用于梯度计算。为了保持稳定性,SSE递归函数定义为历史状态和最新状态的加权平均,更新方程为:其中:
尽管从概念上讲很重要,但是
SSE并未在理论上证明:通过反复应用上述公式节点状态会逐渐收敛到不动点fixed point。
3.4 ConvGNN
图卷积神经网络
ConvGNN和递归图神经网络密切相关。ConvGNN不是使用收缩约束的映射来迭代节点状态,而是使用固定数量的layer,其中每层具有不同的权重。下图说明了这一主要区别:- 图
(a):RecGNN使用相同的graph recurrent layer:Grec来更新节点representation。 - 图
(b):ConvGNN使用不同的graph convolutional layer:GConv来更新节点representation。
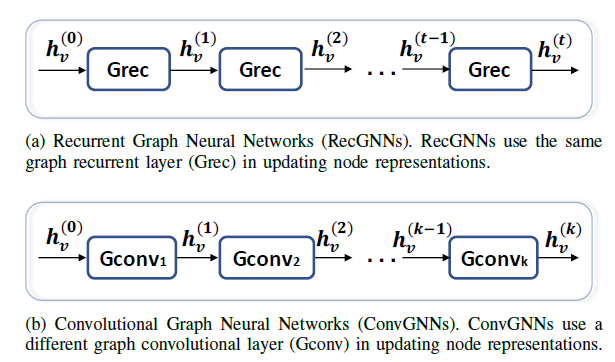
- 图
由于图卷积更有效、更方便与其它神经网络进行组合,因此近年来
ConvGNN的普及非常迅速。ConvGNN可以分为两类:基于谱域spectral-based、基于空域spatial-based。- 基于谱域的方法通过从图信号处理的角度引入滤波器来定义图卷积,其中图卷积运算被解释为从图信号中去除噪声。
- 基于空域的方法继承了
RecGNN的思想,它通过消息传播来定义图卷积。
自从
GCN弥合了基于谱域方法和基于空域方法之间的gap,基于空域的方法由于其卓越的效率efficiency、灵活性flexibility、通用性generality而得到迅速发展。
3.4.1 基于谱域的 ConvGNN
基于谱域的
ConvGNN在图信号处理中具有扎实的数学基础。他们认为图是无向的,归一化的图拉普拉斯矩阵是无向图的数学表述,定义为degree矩阵(一个对角矩阵)。
归一化的图拉普拉斯矩阵是实对称的、半正定的矩阵,因此可以对其进行特征值分解:
其中:
eigenvector组成的矩阵,其中
在图信号处理领域,一个图信号
feature vector,其中对应的图傅里叶逆变换为:
图傅里叶变换将输入的图信号投影到正交空间,正交基是由归一化的图拉普拉斯矩阵的特征向量构成。图傅里叶变换后的信号
这刚好就是图傅里叶逆变换。
因此对输入信号
其中
如果我们定义一个滤波器为:
所有的谱域卷积都遵从这个公式,但是不同的方法选择不同的滤波器
Spectral Convolutional Neural Network:Spectral CNN假设图信号是多通道的,通道假设网络有多层,其中第
Spectral CNN对于每个通道采用多个卷积层来生成多通道输出。对于第其中:
由于图拉普拉斯矩阵的特征分解
eigendecomposition,Spectral CNN面临三个限制:- 首先,对图的任何扰动都会导致特征根
eigenbasis的变化。 - 其次,学习的滤波器是
transductive的,它无法应用于具有不同结构的图。 - 最后,特征分解计算复杂度为
ChebNet和GCN通过进行一些近似和简化将计算复杂度降低到
Chebyshev Spectral CNN:ChebNet通过切比雪夫多项式来逼近滤波器其中
[-1,1]之间的对角矩阵。切比雪夫多项式定义为:
因此图信号
定义
ChebNet卷积公式:作为对
Spectral CNN的改进,ChebNet定义的滤波器是空间局部性的,这意味着滤波器可以独立于图的大小而抽取局部特征。另外,
ChebNet将频谱spectrum线性映射到[-1,1]之间(即线性映射:CayleyNet进一步使用参数为有理复函数rational complex function的Cayley多项式来捕获窄带信号narrow frequency band。CayleyNet的谱图卷积定义为:其中:
Re(.)返回复数的实部。Cayley滤波器的谱spectrum。
CayleyNet不仅可以保持空间局部性spatial locality,而且ChebNet可以视为CayleyNet的特例。Graph Convolutional Network:GCN对ChebNet采用一阶近似。假设ChebNet卷积公式近似为:为限制参数数量从而缓解过拟合,
GCN进一步假定为支持多通道输入和多通道输出,
GCN进一步将上式转换为:其中:
由于使用
GCN数值不稳定。为解决该问题,GCN应用了归一化技巧,将GCN虽然是基于谱域的方法,也可以解释为基于空域的方法。从基于空域的角度来看,GCN可以视为聚合节点邻域中的特征信息。即最近的一些工作通过探索某些对称矩阵来代替邻接矩阵从而对
GCN进行增量改进incremental improvement。Adaptive Graph Convolutional Network:AGCN学习隐藏的结构关系,这种关系未被图的邻接矩阵所给出。AGCN通过一个可学习的距离函数来构造一个所谓的残差图邻接矩阵residual graph adjacency matrix。这个距离函数将两个节点的特征作为输入。Dual Graph Convolutional Network:DGCN引入双图卷积体系架构,它有两个并行的图卷积层。这两个图卷积层共享参数,但是分别使用归一化的邻接矩阵positive pointwise mutual information:PPMI矩阵。PPMI矩阵通过从图上采样的随机游走来捕获节点的共现信息,定义为:其中:
PPMI值。pair对的集合,
通过集成
ensembling来自双图卷积层的输出,DGCN可以对局部结构信息和全局结构信息进行编码,无需堆叠多个图卷积层。
3.4.2 基于空域的 ConvGNN
和在图像上进行卷积操作的传统
CNN类似,基于空域的方法基于节点的空间关系定义图卷积。图像可以被视为图的一种特殊形式,其中:图像上每个像素代表一个节点,每个像素直接与其附近的像素相连。在图像上应用一个
3x3的卷积可以获得每个通道上中心节点及其邻居(共9个节点)像素值的加权均值。类似地,基于空域的图卷积将中心节点的
representation和邻居的representation进行卷积,从而得到中心节点的更新representation。从另一个角度来看,基于空域的
ConvGNN和RecGNN共享相同的消息传递思想。空域图卷积运算本质上是沿着edge传播节点信息。Neural Network for Graphs:NN4G和GNN*同一时期被提出,它是针对基于空域的ConvGNN的第一项工作。和
RecGNN截然不同的是,NN4G通过每层具有独立参数的组合神经网络体系架构来学习节点的相互依赖关系。节点的邻域可以通过体系结构的增量构建来扩张。NN4G通过直接聚合节点的邻域信息来执行图卷积,它还使用残差链接residual connection以及跳跃连接skip connection来记住每一层的信息。最终NN4G的节点状态更新方程为:其中:
上式也可以写作矩阵形式:
这类似于
GCN的形式。一个区别是NN4G使用未归一化的邻接矩阵,这可能潜在地导致节点的hidden state具有极为不同的量级。Contextual Graph Markov Model:CGMM受到NN4G启发,从而提出了一种概率模型。CGMM在保持空间局部性的同时,还具有可解释性的优势。Diffusion Convolutional Neural Network:DCNN将图卷积视为扩散过程。它假定信息以一定的转移概率从一个节点转移到相邻节点之一,从而使得信息分布可以在几轮之后达到平衡。DCNN将扩散图卷积diffusion graph convolution定义为:其中:
注意在
DCNN中,hidden representation矩阵hidden representation矩阵最终
DCNN拼接由于扩散过程的平稳分布是概率转移矩阵的幂级数的总和,因此
Diffusion Graph Convolution:DGC将每个扩散step中的结果相加,而不是进行拼接。它定义扩散图卷积diffusion graph convolution为:其中:
representation维度。这使得hidden representation矩阵
使用转移概率矩阵的幂意味着距离遥远的邻居向中心节点贡献的信息很少。
PGC-DGCNN根据最短路径增加遥远邻居的贡献,它定义最短路径邻接矩阵转移概率矩阵的幂次意味着邻居节点的重要性随着距离的增加呈指数型衰减,而这里的权重设定为
1。通过使用超参数
receptive field size,PGC-DGCNN引入了图卷积运算如下:其中:
representation的维度。
由于最短路径邻接矩阵
Partition Graph Convolution:PGC根据某些原则(不限于最短路径)将节点的邻居划分为PGC将具有不同参数的GCN应用于每个邻居分组,并对结果求和:其中:
representation,representation的维度。
类似于注意力机制中的
multi-head。Message Passing Neural Network:MPNN总结了基于空域的ConvGNN的通用框架。MPNN将图卷积视为一个消息传递过程,其中信息可以直接从一个节点沿着边传递到另一个节点。MPNN执行消息传递函数(即空间图卷积)定义为:
其中:
representation,
在得到每个节点的
hidden representation之后,可以将node-level预测任务,或者传递给readout函数从而执行graph-level预测任务。readout函数基于节点hidden representation从而生成整个图的representation:其中
readout函数。虽然
MPNN可以通过选择不同形式的cover很多现有的GNN模型,但是Graph Isomorphism Network:GIN发现:基于MPNN的方法无法根据它们生成的graph embedding来区分不同的图结构。为弥补这一缺陷,
GIN通过可学习的参数其中
由于节点的邻居数量可能从
1到1000甚至更多,因此获取节点的全部邻居效率太低。GraphSAGE采用采样技术为每个节点获取固定数量的邻居,并定义图卷积为:其中:
representation,
聚合函数需要满足排列不变性
permutation invariant,如均值函数、求和函数、最大值函数等。Graph Attention Network:GAT假设邻居节点对于中心节点的贡献既不像GraphSAGE一样都是1(即所有邻居节点对于中心节点的贡献都相同)、也不像GCN一样预先定义(权重为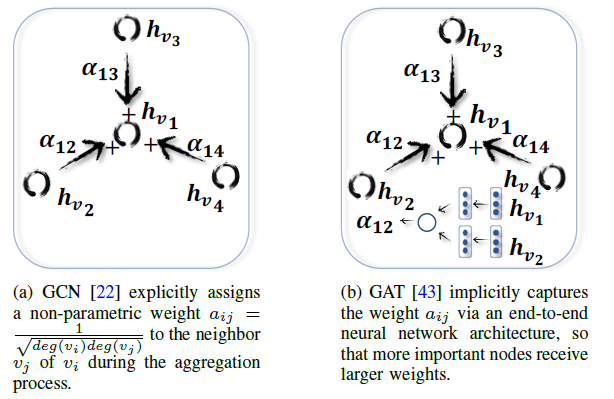
GAT采用注意力机制来学习两个相连节点之间的相对权重,它定义图卷积运算为:其中
其中:
LeakyReLU激活函数。softmax函数可以确保节点1.0。
GAT进一步执行multi-head attention从而提高模型的表达能力。在节点分类任务上,GAT相对于GraphSAGE有着显著的提升。GAT假设attention head的贡献是相等的,而Gated Attention Network:GAAN认为不同的attention head的贡献是不同的。GAAN引入了一种self-attention机制,该机制为每个attention head计算一个额外的注意力得分。除了在空间上
spatially应用图注意力之外,GeniePath进一步提出了一种类似于LSTM的门控机制,从而控制跨图卷积层的信息流。还有其它有趣的图注意力模型,但是它们不属于
ConvGNN框架。Mixture Model Network:MoNet采用不同的方法为节点的邻居分配不同的权重,它引入节点伪坐标pseudo-coordinates以确定节点及其邻居之间的相对位置。一旦知道两个节点之间的相对位置,则权重函数会根据相对位置计算这两个节点之间的相对权重。这样,图滤波器的参数可以在不同位置location之间共享。在
MoNet框架下,通过构造非参数的nonparametric权重函数,几种流形manifold方法如Geodesic CNN: GCNN、Anisotropic CNN : ACNN、Spline CNN,某些图卷积方法如GCN、DCNN,都可以视作MoNet的特例。MoNet还提出了一个具有可学习参数的高斯核,从而自适应地学习权重函数。另一类独特的方法是:根据某些标准对节点的邻居进行排名
ranking,并将每个排名与可学习的权重相关联,从而在不同位置实现权重共享。PATCHY-SAN根据它们的图标签graph label对每个节点的邻居进行排序,并选择top q个邻居。图标签本质上是节点得分,可以通过节点degree、节点中心度centrality、节点Weisfeiler-Lehman color得到。由于每个节点现在都有固定数量的有序邻居,因此可以将图结构数据转换为网格结构的数据。
PATCHY-SAN采用标准的1D卷积滤波器来聚合邻域特征信息,其中滤波器权重的顺序和节点邻居的顺序相对应。PATCHY-SAN的排名准则仅考虑图结构,这需要大量计算才能进行数据处理。Large-scale Learnable Graph Convolutional Network:LGCN根据节点特征信息对节点的邻居进行排名。对于每个节点,LGCN都会拼装assemble一个由其邻域组成的特征矩阵,并沿着每一列(行代表节点、列代表特征)对该矩阵进行排序。排序后的特征矩阵的前下图中,矩阵第一行是中心节点的特征向量,它不参与排序。后面
4行是排序之后的。排序时,不同列之间相互独立排序。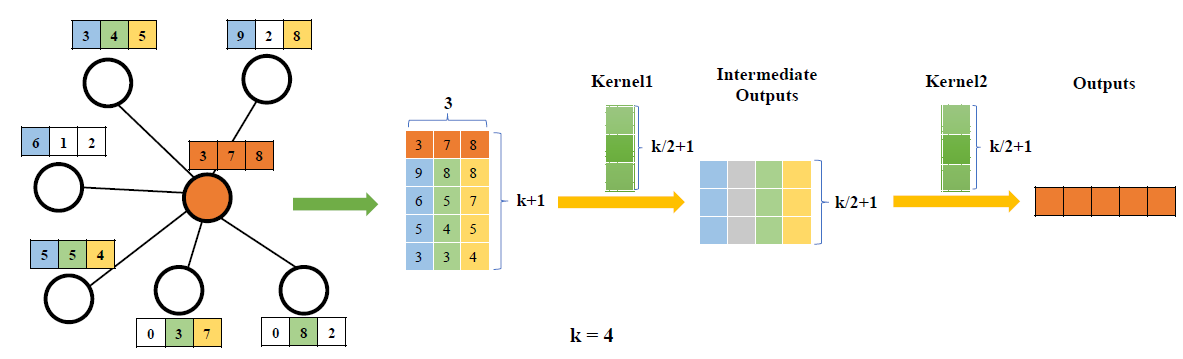
3.4.3 空域 ConvGNN 训练效率
通常训练诸如
GCN之类的ConvGNN需要将整个图数据和所有节点的中间状态保存到内存中,因此ConvGNN的full-batch训练算法遭受内存溢出的困扰,尤其是当一个图包含数百万节点时。为降低内存需求,
GraphSAGE提出了一种针对ConvGNN的batch训练算法。对于batch中的每个节点,它以固定大小递归采样节点邻域从而构成一棵以该节点为根节点的采样树。对于每棵采样树,GraphSAGE通过从下到上分层聚合节点的hidden representation来计算根节点的hidden representation。Fast Learning with Graph Convolutional Network:FastGCN为每个图卷积层采样固定数量的节点,而不是像GraphSAGE那样为每个节点采样固定数量的邻居。它将图卷积解释为概率测度下节点embedding函数的积分变换,然后采用蒙特卡洛近似Monte Carlo approximation以及方差缩减技术variance reduction technique来加速训练过程。由于
FastGCN针对每一层独立采样节点,因此层间连接可能很稀疏。《Adaptive sampling towards fast graph representation learning》提出一种自适应的逐层采样方法,其中较低层的节点采样以上一层已经采样到的节点为条件。和FastGCN相比,该方法以更复杂的采样方案为代价实现了更高的准确率。Stochastic Training of Graph Convolutional Networks:StoGCN使用历史的节点representation作为控制变量从而将图卷积的感受野尺寸receptive field size缩减到任意小的尺度scale。即使每个节点仅有两个邻居(其中一个是它自己),StoGCN仍然可以达到可比的comparable性能。但是,StoGCN仍然必须保存所有节点的中间状态,这对于大型图来讲是非常消耗内存的。Cluster-GCN使用图聚类算法对子图进行采样,并对所采样的子图中的节点执行图卷积。由于邻域搜索被限制在采样的子图中,因此Cluster-GCN能够处理更大的图,并同时使用更少的时间、更少的内存来训练更深的体系架构。对于现有的
ConvGNN训练算法,Cluster-GCN特别提供了时间复杂度和内存复杂度的直接比较,如下表所示。其中batch size、hidden representation维度都是GCN是full-batch训练方法,它作为baseline。GraphSAGE以牺牲时间效率来节省内存。同时随着GraphSAGE的时间和内存复杂度呈指数级增长。StoGCN的时间复杂度最高,并且内存瓶颈仍未解决。但是,StoGCN可以通过很小的Cluster-GCN的时间复杂度和baseline相同,因为它没有引入冗余计算。- 所有方法中,
ClusterGCN实现了最低的内存复杂度。

3.4 .4 spectral vs spatial
谱域模型
spectral model具有图信号处理的理论基础,可以通过设计新的图信号滤波器来构建新的ConvGNN。但是,由于效率efficiency、通用性generality、灵活性flexibility等问题,空域模型spatial model要优于谱域模型。首先,谱域模型的效率不如空域模型。谱域模型要么需要执行特征向量
eigenvector计算,要么需要同时处理整个图。空域模型对于大型图更具有可扩展性
scalable,因为它通过信息传播直接在图域graph domain中执行卷积。计算可以在一个batch的节点上进行,而不是整个图。其次,依赖于图傅里叶基
graph Fourier basis的谱域模型无法泛化到新的图。因为谱域模型假设图是固定的,对图的任何扰动都将导致本征基eigenbasis的变化。另一方面,空域模型在每个节点的局部执行图卷积,其中模型权重可以在不同位置、不同结构之间轻松共享。
最后,谱域模型仅限于在无向图上运行,而空域模型可以更灵活地处理多种数据源
multi-source的图输入graph input,如edge input、有向图、有符号图、异质图等。因为这些图输入可以轻松地集成到空域模型的聚合函数中。
3.4.5 Graph Pooling 模型
GNN生成节点特征后,我们可以将其用于最终任务。但是,直接使用所有节点的特征可能在计算上具有挑战性,因此需要一种降采样策略down-sampling strategy。根据不同的任务目标、以及降采样在网络中扮演的角色,该策略有不同的称呼:pooling操作:旨在通过对所有节点representation进行降采样从而生成规模更小的representation从而减少参数大小,进而缓解过拟合、实现置换不变性permutation invariance、以及解决计算复杂度问题。readout操作:旨在基于节点representation生成graph-level representation。
它们的机制都非常相似,因此这里我们用池化
pooling来指代用于GNN中的各种降采样策略。在一些早期的工作中,图粗化算法
graph coarsening algorithm使用特征分解eigen-decomposition来基于图的拓扑结构来粗化图。但是这些方法存在时间复杂度问题。Graclus算法是特征分解的替代方法,用于计算原始图的聚类版本clustering version。有一些近期的工作将它作为池化操作来粗化图。如今,
mean/max/sum池化是实现降采样的最原始、最有效的方法,因为在池化窗口中计算mean/max/sum值非常快:其中
《Deep convolutional networks on graph-structured data》表明:在网络开始时执行简单的max/mean池化对于降低图域的维度、缓解昂贵的图傅里叶变换的成本尤为重要。另外,
《Graph echo state networks》、《Neural message passing for quantum chemistry》、《On filter size in graph convolutional networks》也是用注意力机制来改进mean/sum池化。
即使使用注意力机制,
reduction操作(如sum pooling)效果也不理想,因为它使得embedding低效inefficient:无论图的尺寸size如何,都生成固定尺寸fixed-size的embedding。《Order matters: Sequence to sequence for sets》提出了Set2Set方法来生成一个随着输入尺寸而增加的memory embedding。然后它实现了一个LSTM,该LSTM试图在reduction操作之前将order-dependent信息集成到memory embedding中;否则销毁destroy该信息。《Convolutional neural networks on graphs with fast localized spectral filtering》以另一种方式通过以有意义的方式重排图的节点来解决这个问题。他们在自己的方法ChebNet中设计了一种有效的池化策略:- 首先通过
Graclus算法将输入图粗化为多个level。 - 粗化之后,输入图的节点及其粗化版本重排为为平衡二叉树。
- 然后对平衡二叉树从底部到顶部任意聚合,这将使得相似的节点排列在一起。
池化这种重排的信号要比池化原始信号有效得多。
- 首先通过
《An end-to-end deep learning architecture for graph classification》提出了DGCNN,它具有类似的叫做SortPooling的池化策略,该策略通过将节点重排为有意义的顺序来执行池化。和
ChebNet不同,DGCNN根据节点在图中的结构角色对节点进行排序。来自空间图卷积的、图的无序的节点特征被视为连续的WL colors,然后将它们用于对节点进行排序。除了对节点特征进行排序外,它还通过截断/扩展truncating/extending节点特征矩阵,从而将图的大小归一化为- 如果
- 如果
- 如果
上述池化方法主要考虑图的特征而忽略图的结构信息。最近提出了一个可微的池化方法
DiffPool,它可以生成图的层次representation。和所有之前的粗化方法相比,DiffPool不仅简单地将图上的节点聚类,而且还学习了第cluster assignment metrix矩阵
其中:
representation(粗化后的节点)。ConvGNN。
该方法的核心思想是学习同时考虑图的拓扑结构和特征信息的节点分配
node assignment,因此上式可以使用任何标准的ConvGNN实现(因为ConvGNN同时使用图的拓扑结构和特征信息)。但是DiffPool的缺点是在池化后会生成稠密图dense graph,此后的计算复杂度变成最近提出了
SAGPool方法,该方法同时考虑节点的特征信息和图拓扑结构信息,并以一种self-attention的方式学习了池化。总体而言,池化是减小图尺寸的基本操作。如何提高池化的有效性、降低计算复杂度是一个尚待研究的问题。
3.4.6 理论分析
我们从不同角度讨论图神经网络的理论基础。
感受野形状
shape of receptive field:节点的感受野是有助于确定其final node representation的一组节点。当组合多个空间图卷积层时,每新增一层,节点的感受野就会向更远的邻居前进一步。《Neural network for graphs: A contextual constructive approach》证明:存在有限数量的空间图卷积层,使得对于任意节点ConvGNN能够通过堆叠局部的图卷积层来抽取全局信息。VC维:VC维是模型复杂度的度量,定义为模型能够打散shattere的最大样本数。分析
GNN的VC维的工作很少。《The vapnik–chervonenkis dimension of graph and recursive neural networks》指出,给定模型参数数量- 如果使用
sigmoid或者tanh激活函数,则GNN*的VC维为 - 如果使用分段多项式激活函数,则
GNN*的VC维为
该结果表明:如果使用
sigmoid或者tanh激活函数,则GNN*的模型复杂度会随着- 如果使用
图同构
graph isomorphism:如果两个图在拓扑上相同,则它们是同构的。给定两个非同构
non-isomorphic图《How powerful are graph neural networks 》证明:如果GNN将embedding,则可以通过Weisfeiler-Lehman:WL同构测试将这两个图识别为非同构的。他们表示:常见的GNN(如GCN,GraphSAGE) 无法区分不同的图结构。论文进一步证明:如果
GNN的聚合函数和readout函数是单射injective的,则GNN在区分同构图的能力上最多和WL test一样。单射函数
等变性和不变性
equivariance and invariance:执行node-level任务时,GNN必须是等变函数equivariant function;而执行graph-level任务时,GNN必须是不变函数invariant function。- 对于
node-level任务,令GNN,permutation matrix(即单位矩阵GNN是等变的equivariant。 - 对于
graph-level任务,令GNN,如果满足GNN是不变的invariant。
为了实现等变性
equivariance或不变性invariance,GNN的组件components必须满足对节点顺序是不变的invariant。论文《Invariant and equivariant graph networks》从理论上研究了图数据的排列不变性permutation invariant、排列等变性permutation equivariant的线性层的特点。- 对于
通用逼近
universal approximation:众所周知,具有单层hidden layer的MLP前馈神经网络可以逼近任何Borel可测函数。但是很少有人研究GNN的通用逼近能力。《Universal approximation capability of cascade correlation for structures》证明级联相关cascade correlation可以逼近结构化输出的函数。《Computational capabilities of graph neural networks》证明RecGNN可以逼近任何函数到任意精度,该函数保持展开等价性unfolding equivalence。如果两个节点的展开树unfolding trees相同,则这两个节点的展开等价。其中节点的展开树是通过以一定深度迭代扩展节点的邻域来构造的。《How powerful are graph neural networks》表明:在消息传递框架下ConvGNN不是在多集合multisets上定义的连续函数的通用逼近器。《Invariant and equivariant graph networks》证明了不变图网络invariant graph network可以逼近图上定义的任意不变函数invariant function。
3.5 GAE
图自编码器
Graph Autoencoder: GAE是一种深度神经网络架构,可以将节点映射到潜在表示latent representation,然后从潜在表示中解码图信息。GAE可用于学习graph embedding或者生成新图,下表总结了部分GAE的主要特点。下文中,我们从graph embedding和graph generation角度简要概述了GAE。
3.5.1 Graph Embedding
graph embedding是节点的低维向量表示,可以保留节点的拓扑信息。GAE使用编码器抽取graph embedding、并使用解码器来强迫graph embedding保留图拓扑信息(如PPMI矩阵和邻接矩阵)从而学习graph embedding。早期的方法主要采用多层感知机
MLP来构建用于学习graph embedding的GAE。Deep Neural Network for Graph Representations:DNGR使用堆叠的降噪自编码器denoising autoencoder通过MLP来编码和解码PPMI矩阵。同时,
Structural Deep Network Embedding:SDNE使用堆叠自编码器来同时保存节点的一阶邻近度first-order proximity和二阶邻近度second-order proximity。SDNE在编码器输出和解码器输出上分别提出了损失函数。第一个损失函数针对编码器输出,通过最小化节点的
graph embedding及其邻居的graph embedding之间的距离,来迫使学到的graph embedding保持节点的一阶邻近度。这个损失函数定义为:其中:
multi-layer perceptron:MLP组成的编码器。
第二个损失函数针对解码器输出,通过最小化自编码器输入及其重构的输出之间的距离,来迫使学到的
graph embedding保留节点的二阶邻近度。这个损失函数定义为:其中:
MLP组成的解码器。这迫使模型更关注相连节点的损失。
这里自编码器的输入为节点的邻接向量,因此重构节点的邻接向量意味着保持节点的邻域,即二阶邻近度。
DNGR和SDNE仅考虑和节点pair对之间的连通性有关的节点结构信息,他们忽略节点可能包含描述节点本身属性的特征信息。《Variational graph auto-encoders》提出了Graph Autoencoder(记作GAE*以示区分)来利用GCN同时编码节点结构信息和节点特征信息。GAE*的编码器由两个图卷积层组成,其形式为:其中:
graph embedding矩阵。ReLU。
GAE*的解码器旨在通过重构图邻接矩阵,从而从节点的embedding中解码节点之间的关系信息。解码器定义为:其中
embedding。GAE*通过最小化给定真实邻接矩阵negative cross entropy来训练。由于自编码器的容量
capacity,简单地重构图邻接矩阵可能会导致过拟合。《Variational graph auto-encoders》同时提出了变分图自编码器Variational Graph Autoencoder:VGAE,它是GAE的变分版本,用于学习数据分布。VGAE优化变分下限其中:
KL(.)为KL散度函数,用于衡量两个分布之间的距离。
根据上述公式,
VGAE假设经验分布损失函数的第一项要求最大后验分布,第二项要求经验分布
为进一步强制经验分布
Adversarially Regularized Variational Graph Autoencoder:ARVGA采用了生成对抗网络generative adversarial network:GAN的方案。GAN在训练生成模型时会在生成器generator和判别器discriminator之间进行竞争比赛:生成器试图生成尽可能真实的fake样本,而判别器试图将fake样本和真实样本区分开。受
GAN的启发,ARVGA努力学习一种编码器,该编码器产生的经验分布类似于
GAE*,GraphSAGE用两个图卷积层编码节点特征。GraphSAGE并没有优化重建损失,而是表明两个节点之间的关系信息可以通过负采样来保留,其损失函数为:其中:
- 节点
negative sampling distribution
该损失函数本质上是迫使相邻的节点具有相似的
representation、距离遥远的节点具有不同的representation。- 节点
DGI和GraphSAGE不同,它通过最大化局部互信息local mutual information来驱动局部网络embedding(local network embedding)来捕获全局结构信息。从实验上看,它比GraphSAGE有明显改进。上述方法本质上是通过解决链接预测问题来学习
graph embedding。但是,图的稀疏性导致postive节点pair对的数量远远少于negative节点pair对的数量。为缓解学习
graph embedding中的数据稀疏性问题,另一个方向的工作通过随机排列或随机游走将图转换为序列。通过这种方式,一些适用于序列的深度学习方法可以直接用于处理graph。Deep Recursive Network Embedding:DRNE假设节点的graph embedding应该近似于它邻域节点embedding的聚合。它采用LSTM来聚合节点的邻域embedding。DRNE的重构误差定义为:其中:
embedding,它直接通过一个字典look-up得到。- 节点
degree排序后作为LSTM网络的输入。
如公式所示,
DRNE通过LSTM来隐式学到graph embedding,而不是直接使用LSTM来生成graph embedding。它避免了LSTM对于节点序列的排列不是不变invariant的问题。对抗正则化自编码器
Adversarially Regularized Autoencoder:NetRA提出一个带通用损失函数的graph encoder-decoder框架。其损失函数定义为:其中:
dist(.)为节点embeddingembeddingenc(.)和dec(.)分别为编码器和解码器。它们都是LSTM网络,使用以节点
类似于
ARVGA,NetRA通过对抗训练将学到的graph embedding正则化到先验分布中。尽管NetRA忽略了LSTM网络中节点的排列不变性的问题,但实验结果验证了NetARA的有效性。
3.5.2 Graph Generation
给定多个图,
GAE通过将图编码为hidden representation并根据这个representation解码图结构,从而可以学到图的生成分布generative distribution。大多数图生成的GAE旨在解决分子图molecular graph生成问题,这在药物发现中具有很高的实用价值。这些方法要么以顺序方式sequential manner、要么以全局方式global manner生成一个新的图。顺序方式通过逐步生成节点和边来生成图。
《Automatic chemical design using a data-driven continuous representation of molecules》、《Grammar variational autoencoder》、《Syntax-directed variational autoencoder for molecule generation》用深度CNN作为编码器、深度RNN作为解码器,对名为SMILES的分子图字符串的生成过程建模。尽管这些方法是
domain-specific,但是它们通过将节点、边迭代地添加到图上直到满足特定条件为止,从而可以适用于一般的图生成。Deep Generative Model of Graphs:DeepGMG假设图的概率是所有可能的节点排列之和:其中
DeepGMG捕获图中所有节点和边的、复杂的联合概率。DeepGMG通过做出一系列决策来生成图,即:是否添加节点、添加哪个节点、是否对这个新节点添加边、这个新节点连接到哪个节点。生成节点和边的决策过程取决于这个不断增长growing图的节点状态和图状态,其中节点状态和图状态通过RecGNN来更新。在另一项工作中,
GraphRNN提出一个graph-level的RNN以及一个edge-level的RNN来建模节点和边的生成过程。每次graph-level RNN都会向节点序列中添加一个新的节点,而edge-level RNN生成一个binary sequence,它指示新节点和节点序列中之前生成的节点之间的连接。
全局方式可以一次性生成整个图。
图变分自编码器
Graph Variational Autoencoder:GraphVAE将节点和边的存在建模为独立随机变量。通过假设后验分布posterior distributiongenerative distributionGraphVAE优化变分下界:其中:
使用
ConvGNN作为编码器、使用简单的MLP作为解码器,GraphVAE输出生成的图及其邻接矩阵、节点属性、边属性。控制生成图的全局属性(如图的连接性
connectivity、有效性validity,以及节点兼容性compatibility)具有挑战性。正则化图变分自编码器Regularized Graph Variational Autoencoder:RGVAE进一步在图变分自编码器上施加了有效性约束validity constraint,从而正则化解码器的输出分布。分子生成对抗网络
Molecular Generative Adversarial Network:MolGAN整合了ConvGNN、GAN、以及强化学习技术从而生成具有所需特性的图。MolGAN由生成器和判别器组成,它们相互竞争从而提高生成器的真实性authenticity。在MolGAN中,生成器试图提出一个fake图及其特征矩阵,而判别器目标是将fake数据和真实数据中区分开。另外,引入了和判别器并行的奖励网络,从而鼓励生成的图具有某些特性。
NetGAN将LSTM和Wasserstein GAN结合起来,通过基于随机游走的方法生成图。NetGAN训练生成器通过LSTM网络生成合理的随机游走,并强迫判别器从真实的随机游走中识别fake随机游走。训练好之后,通过归一化基于生成器产生的随机游走而计算得到的节点共现矩阵,从而得到新的图。
总之:
- 顺序方式将图线性化为序列。由于存在环结构,因此它们可能会丢失结构信息。
- 全局方式可以一次性生成一个图。由于
GAE的输出空间可达scalable。
3.6 SPATIAL-TEMPORAL GNN
在很多实际应用中,图在结构和输入方面都是动态的。时空图神经网络
patial-temporal graph neural network: STGNN在捕获图的动态性中占据重要位置。该类别下的方法旨在建模动态的节点输入,同时假设已连接节点之间的相互依赖性。STGNN假设图的结构不变,需要建模的是节点的动态属性。例如,交通网络由放置在道路上的速度传感器组成,其中传感器之间的边的权重由传感器之间距离决定。由于一条道路的交通状况可能取决于其相邻道路的交通状况,因此执行交通速度预测时,必须考虑空间依赖性。作为解决方案,
STGNN可以同时捕获图的空间依赖性和时间依赖性。STGNN的任务可以是预测节点未来的值或标签,或者预测时空图的graph label。STGNN有两个方向,即:基于RNN的方法RNN-based method、基于CNN的方法CNN-based method。
3.6.1 Rnn-based
大多数基于
RNN的方法通过使用图卷积来过滤传递给RNN单元的input和hidden state来捕获时空依赖性。为了说明这一点,假设一个简单的RNN采用以下形式:其中:
representation矩阵。
在插入图卷积之后,上式变为:
其中
GConv(.)为一个图卷积层。图卷积递归网络
Graph Convolutional Recurrent Network:GCRN结合了LSTM网络和ChebNet。扩散卷积递归神经网络
Diffusion Convolutional Recurrent Neural Network:DCRNN将扩散图卷积层(GRU网络中。此外,DCRNN采用encoder-decoder框架来预测未来另一项同时进行的工作使用
node-level RNN和edge-level RNN来处理时间信息的不同方面aspect。Structural-RNN提出了一个循环框架来预测每个time step的节点标签。它包含两种RNN,即:node-RNN:用于传递每个节点的时间信息。edge-RNN:用于传递每条边的时间信息。
为整合空间信息,
node-RNN将edge-RNN的输出作为输入。由于为不同的节点和边采用不同的
RNN会大大增加模型的复杂度,因此Structural-RNN将节点和边进行语义分组semantic group。相同语义组中的节点或边共享相同的RNN模型,从而降低计算成本。
3.6.2 CNN-based
基于
RNN的方法存在耗时的迭代传播、以及梯度爆炸/消失问题。作为替代方案,基于CNN的方法以非递归的方式处理时空图,具有计算并行、梯度稳定、内存需求低等优点。基于
CNN的方法将1D-CNN层和图卷积层交织从而分别学习时间依赖性和空间依赖性。假设时空图神经网络的输入为张量
1D-CNN层在给定空间,聚合时间。
而图卷积层在
给定时间,聚合空间。
CGCN将一维卷积层与ChebNet或GCN层整合在一起。它通过按顺序堆叠一个门控1D卷积层、一个图卷积层、另一个门控1D卷积层,从而构成时空块spatial-temporal block。ST-GCN使用1D卷积层和PGC层(之前的方法都使用预定义的图结构,他们假设预定义的图结构反映了节点之间的真正依赖关系。
但是,利用
spatial-temporal setting中的很多图数据快照,可以从数据中自动学习潜在的静态图结构。为了实现这一点,Graph WaveNet提出了一种自适应邻接矩阵来执行图卷积。自适应的邻接矩阵定义为:其中:
Softmax(.)函数沿着行维度进行。source节点embedding。target节点embedding。
通过将
source节点和target节点之间的依赖关系权重。借助基于CNN的复杂时空网络,Graph WaveNet无需提供邻接矩阵即可表现良好。学习潜在的静态空间依赖性可以帮助研究人员发现网络中不同实体之间可解释的、稳定的相关性。但是,某些情况下,学习潜在的动态空间依赖性可以进一步提高模型的精度。例如,在交通网络中,两条道路之间的通行时间
travel time可能取决于它们当前的交通状况。GaAN利用注意力机制通过基于RNN的方法学习动态空间依赖性。注意力函数用于在给定这个边的两个节点的节点输入的情况下,更新边的权重。ASTGCN进一步包括空间注意力函数和时间注意力函数,从而通过基于CNN的方法学习潜在的动态空间相关性和动态时间相关性。
学习潜在空间相关性的共同缺点是,它需要计算每对节点
pair对之间的空间相关性权重,计算复杂度为
3.7 应用 & 方向
由于图结构数据无处不在,因此
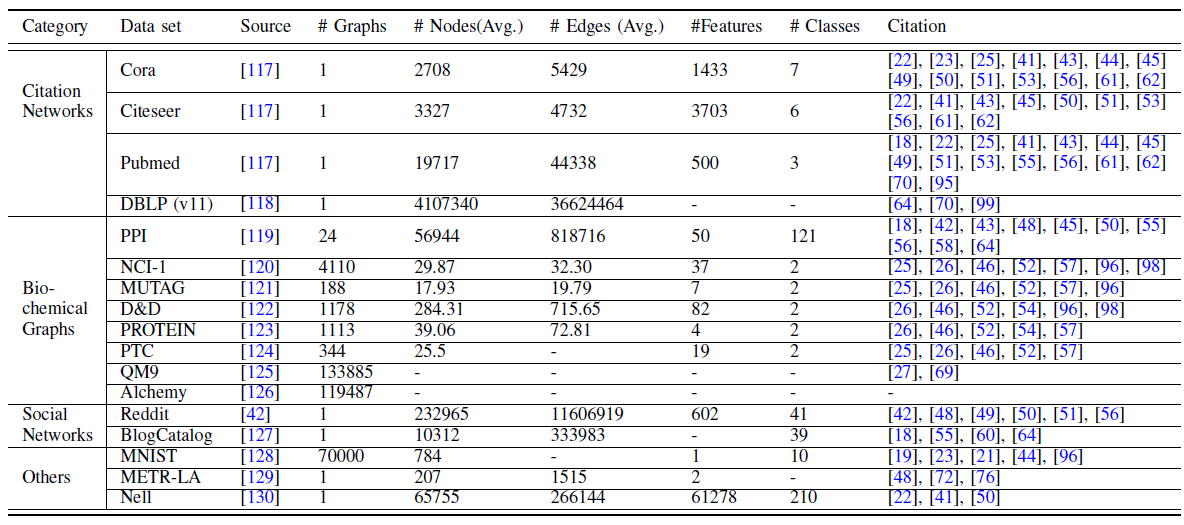
GNN有广泛的应用。这里我们分别总结了benchmark图数据集、评估方法、开源实现。我们还详细介绍了GNN在各个领域的实际应用。数据集:我们将主要的图
benchmark数据集分为四类,即引文网络citation network、生化图biochemical graph、社交网络social network以及其它。我们在下表给出了这些数据集的统计信息。引文网络:由论文、作者、以及它们之间的关系(如引用
citation、作者、合著等关系)组成。尽管引文网络是有向图,但是评估节点分类、链接预测、节点聚类等任务的模型性能时,引文网络通常被视为无向图。流行的引文网络数据集有:
Cora数据集:包含2708篇机器学习论文组成,分为七个类别。每篇论文都由一个文章单词的one-hot向量表示,表示对应的单词是否出在论文中。Citeseer数据集:包含3327篇科学论文,分为六个类别。每篇论文都由一个文章单词的one-hot向量表示,表示对应的单词是否出在论文中。Pubmed数据集:包含19717篇与糖尿病有关的论文。每篇论文都由单词的TF-IDF向量来表示。DBLP数据集:包含数百万计算机科学论文及其作者,是一个大型的引文网络数据集。
生化图:化学分子和化合物可以用化学图
chemical graph表示,原子为节点、化学键为边。NCI-1和NCI-9数据集:分别包含4110和4127个化学化合物,标记它们是否具有活性以阻止人类癌细胞系的生长。MUTAG数据集:包含188种硝基化合物,分别标记它们是芳香族还是杂芳香族。D&D和PROTEIN数据集:将蛋白质表示为图,标记它们是酶还是非酶。PTC数据集:包含344种化合物,标记它们对雄性和雌性大鼠是否具有致癌性。QM9数据集:记录最多含9个重原子的133885个分子的13个物理特性。Alchemy数据集:记录最多含14个重原子的119487个分子的12个量子力学特性。
另一个重要的数据集是
ProteinProtein Interaction network:PPI数据集:包含24个生物学图biological graph,其中节点表示蛋白质,边表示蛋白质之间的相互作用。在PPI中,每个图都与一个人体组织相关联。每个节点的标签都是其生物学状态。社交网络:由在线服务(如
BlogCatalog、Reddit)的用户交互形成。BlogCatalog数据集:一个由博客作者及其社交关系组成的社交网络。博客作者的类别代表他们的个人兴趣。Reddit数据集:从Reddit论坛收集的帖子形成的无向图。如果两个帖子包含同一个用户的讨论,则帖子之间存在链接。每个帖子都有一个标签,标记其所属社区community。
其它:还有几个其它数据集值得一提:
MNIST数据集:包含70000张28 x 28的图像,标记为0~9之间的十个数字。它是经典的手写数字识别数据集。我们可以基于像素位置构造一个
8-nearest-neighbor图,从而将图片转换为graph。METR-LA数据集:一个时空图数据集。它包含洛杉矶高速公路上的207个传感器收集的四个月的交通数据。通过具有高斯阈值的sensor network distance来计算图的邻接矩阵。NELL数据集:从Never-Ending Language Learning项目获得的知识图谱。它由三元组表示的fact组成,其中涉及两个实体及其关系。
节点分类和图分类是评估
RecGNN和ConvGNN性能的常用任务。节点分类:在节点分类中,大多数方法采用对
benchmark数据集(包括Cora,Citeseer,Pubmed,PPI,Reddit)进行标准的train/valid/test划分。它们报告了多次运行测试数据集的平均准确率或F1得分,我们在下表给出了这些方法的实验结果的摘要。注意,这些结果不一定表示严格的比较。
《Pitfalls of graph neural network evaluation》指出,GNN在节点分类任务的性能评估有两个陷阱:- 首先,在所有实验中使用相同的
train/valid/test划分会低估泛化误差。 - 其次,不同的方法采用了不同的训练技术,如超参数调优、参数初始化、学习率衰减、早停技术。
为了进行公平的比较,我们建议读者阅读论文
《Pitfalls of graph neural network evaluation》。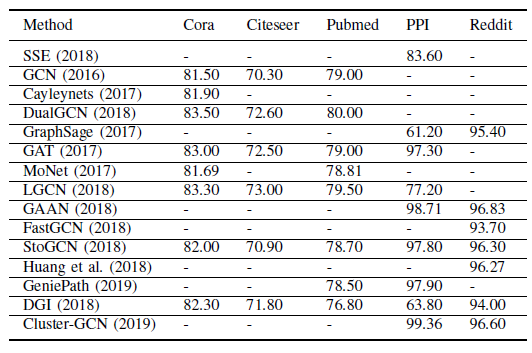
- 首先,在所有实验中使用相同的
图分类:在图分类任务中,研究人员通常采用
10-fold交叉验证进行模型评估。然而,正如
《A fair comparison of graph neural networks for graph classification》所指出的,实验设置是模棱两可的ambiguous,并且在不同论文之间没有统一。具体而言,该论文抛出了在模型选择、模型评估方面对于数据集正确拆分的关注。一个经常遇到的问题是:每个fold的外部测试集都用于模型选择和风险评估。该论文在标准的、统一的评估框架中比较GNN。他们使用一个external的10-fold交叉来评估模型的泛化性能,并使用一个内部holdout技术(具有90%/10%的train/valid拆分)来选择模型。另一种方法是双交叉方法,该方法使用外部的
k-fold交叉验证进行模型评估,使用内部的k-fold交叉验证进行模型选择。可以阅读该论文从而详细比较GNN方法的图分类任务性能。
开源实现:我们在下表中给出了本文涉及到的
GNN模型的开源实现的超链接。另外,PyTorch有一个PyTorch Geometirc的库,它实现了很多GNN;而Deep Graph Library:DGL也提供了很多GNN的快速实现。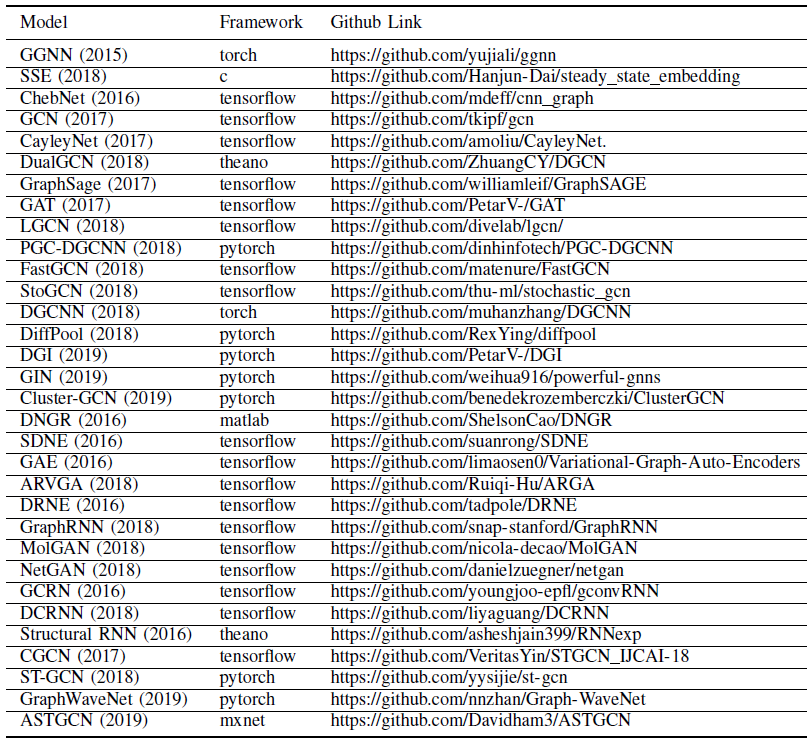
GNN在不同的任务、不同领域中都具有很多应用,这些任务包括节点分类、图分类、graph embedding、图生成、时空图预测、节点聚类、链接预测、图聚类。我们基于以下研究领域详细介绍了一些应用。计算机视觉
Computer vision:GNN在计算机视觉中的应用包括场景图生成scene graph generation、点云分类point clouds classification、动作识别action recognition。识别对象之间的语义关系有助于理解视觉场景背后的含义。场景图生成模型旨在将图像解析为由对象及其语义关系组成的语义图
semantic graph。另一类应用通过给定场景图生成逼真的图像来执行场景图生成的逆向过程。由于自然语言可以解析为语义图,其中每个单词代表一个对象,因此对于给定文字说明的图像合成方法是一种很有前途的解决方案。
通过对点云进行分类
classifying和分段segmenting,LiDAR设备可以 “看到” 周围的环境。点云是通过LiDAR扫描记录的一组3D点。《Dynamic graph cnn for learning on point clouds》、《Large-scale point cloud semantic segmentation with superpoint graphs》、《Rgcnn: Regularized graph cnn for point cloud segmentation》将点云转换为k近邻图或者超点图superpoint graph,并使用ConvGNN探索拓扑结构。识别视频中包含的人的行为可以有助于机器更好地理解视频内容。一些解决方案可以检测视频中人体关节的位置,由骨骼链接的人体关节自然会形成图。给定人体关节位置的时间序列,
《Structural-rnn:Deep learning on spatio-temporal graphs》、《Spatial temporal graph convolutional networks for skeleton-based action recognition》将STGNN用于学习人类行为模式。此外,计算机视觉中
GNN的适用方向数量仍在增长,它包括:human-object交互、few-shot图片分类、语义分割semantic segmentation、视觉推理visual reasoning、知识问答。
自然语言处理
NLP:GNN在NLP中常见的应用是文本分类。GNN利用文档或单词的内部关系来推断文档标签。尽管自然语言数据表现出序列结构,但是它们也可能包含图结构,如语法树。语法树定义了句子中单词之间的句法关系。《Encoding sentences with graph convolutional networks for semantic role labeling》提出了运行在CNN/RNN句子编码器之上的Syntactic GCN。它根据句子的语法依存关系树syntactic dependency tree聚合隐藏的单词representation。《Graph convolutional encoders for syntax-aware neural machine translation》将Syntactic GCN应用于neural machine translation任务。《Exploiting semantics in neural machine translation with graph convolutional networks》进一步采用Syntactic GCN相同的模型来处理句子的语义依赖图semantic dependency graph。graph-to-sequence learning学习在给定摘要单词语义图a semantic graph of abstract words条件下生成具有相同含义的句子,称作Abstract Meaning Representation。《A graph-to-sequence model for amr-to-text generation》提出了一种graph-LSTM来编码graph-level语义信息。《Graph-to-sequence learning using gated graph neural networks》将GGNN应用到graph-to-sequence learning以及neural machine translation。逆任务是
sequence-to-graph learning。给定一个句子生成语义图或知识图在知识发现knowledge discovery中非常有用。交通:在智能交通系统中,准确预测交通网络中的交通速度、交通流量、道路密度至关重要。
《Gaan: Gated attention networks for learning on large and spatiotemporal graphs》、《Diffusion convolutional recurrent neural network: Data-driven traffic forecasting》、《Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting》使用STGNN解决了交通预测问题。他们将交通网络视为时空图,其中节点是安装在道路上的传感器,边的权重是成对节点之间的距离。每个节点具有窗口内的平均交通速度作为动态输入特征。另一个工业级应用是出租车需求预测。给定历史的出租车需求、位置信息、天气数据、事件
event特征,《Deep multi-view spatial-temporal network for taxi demand prediction》结合了LSTM,CNN以及LINE训练的graph embedding从而形成每个位置的联合representation,以预测某个时间间隔内、某个位置所需的出租车数量。推荐系统:基于图的推荐系统将
item和user作为节点。通过利用item-item、user-user、user-item以及内容信息之间的关系,基于图的推荐系统可以生成高质量的推荐。推荐系统的关键是评估
user对于item的重要性得分,这可以转换为链接预测问题。为了预测user和item之间缺失的链接,《Graph convolutional matrix completion》、《Graph convolutional neural networks for web-scale recommender systems》提出了一种使用ConvGNN作为编码器的GAE。《Geometric matrix completion with recurrent multi-graph neural networks》将RNN和图卷积相结合,以学习生成已知评级rating的底层过程underlying process。化学:在化学领域,研究人员应用
GNN来研究分子/化合物的图结构。在分子/化合物图中,节点为原子、边为化学键。节点分类、图分类、图生成是针对分子/化合物图的三个主要任务,目的是学习分子指纹、预测分子特性、推断蛋白质
interface、合成化合物。其它:
GNN的应用不限于上述领域和任务。已有研究者使用GNN对各种问题进行探索探索,如程序验证program verification、程序推理program reasoning、社交影响力预测social influence prediction、对抗攻击和预防adversarial attacks prevention、电器健康记录建模electrical health records modeling、大脑网络brain network、事件检测event detection、组合优化combinatorial optimization等。
尽管
GNN已经证明它在学习图数据方面的能力,但是由于图的复杂性,仍然存在挑战。我们这里提出GNN四个未来的发展方向:模型深度:深度学习的成功在于较深的神经网络体系架构,但是
《Deeper insights into graph convolutional networks for semi-supervised learning》表明:ConvGNN的性能随着图卷积层数量的增加而急剧下降。由于图卷积将相邻节点的representation推向彼此靠近,理论上如果卷积层数量无穷,则所有节点的representation都将收敛到一个点。这就提出了一个问题:即更深的模型是否仍然是学习图数据的好策略?扩展性
trade-off:GNN的可扩展性scalability是以破坏图完整性completeness为代价的。无论是采样还是聚类,模型都会丢失部分图信息。- 通过采样,节点可能会错过它的有影响力的邻居。
- 通过聚类,可能丢失图的独有的结构模式。
如何权衡算法的可扩展性和图的完整性可能是未来的研究方向。
异质性
Heterogenity:当前的大多数GNN假设图为同质图homogeneous。难以将当前的GNN直接应用于异质图,因为异质图可能包含不同类型的节点和边,或者不同形式的节点输入、边输入(如图像和文本)。因此,应该设计新的方法来处理异质图。动态性
Dynamicity:图在本质上是动态的,因为节点或边可能出现或消失,并且节点/边的输入可能会随着时间变化。需要新的图卷积从而适应图的动态性。虽然STGNN可以部分解决图的动态问题,但是很少有人考虑在动态空间关系的情况下如何执行图卷积。