一、Mixed Precision Training [2017] [粗读]
论文:
《Mixed Precision Training》
论文是关于混合精度训练的,考虑到混合精度训练的思想已经广为人知,因此这里仅做粗读。
Introduction:略(参考原始论文)。相关工作:略(参考原始论文)。
1.1 方法
我们介绍了
training with FP16的关键技术,同时仍然匹配FP32 training session的model accuracy:single-precision master weights and updates、loss-scaling、accumulating FP16 products into FP32。单精度浮点数为
float32、双精度浮点数为float64。
1.1.1 FP32 Master Copy Of Weights
在混合精度训练中,权重、
activations以及梯度以FP16格式存储。为了匹配FP32网络的准确率,我们维护权重的一份FP32 master copy,并在optimizer step中用weight gradient来更新它。在每次迭代中,使用master weights的FP16 copy进行正向传播和反向传播,将FP32 training所需的存储和带宽减半。Figure 1说明了这种混合精度训练过程。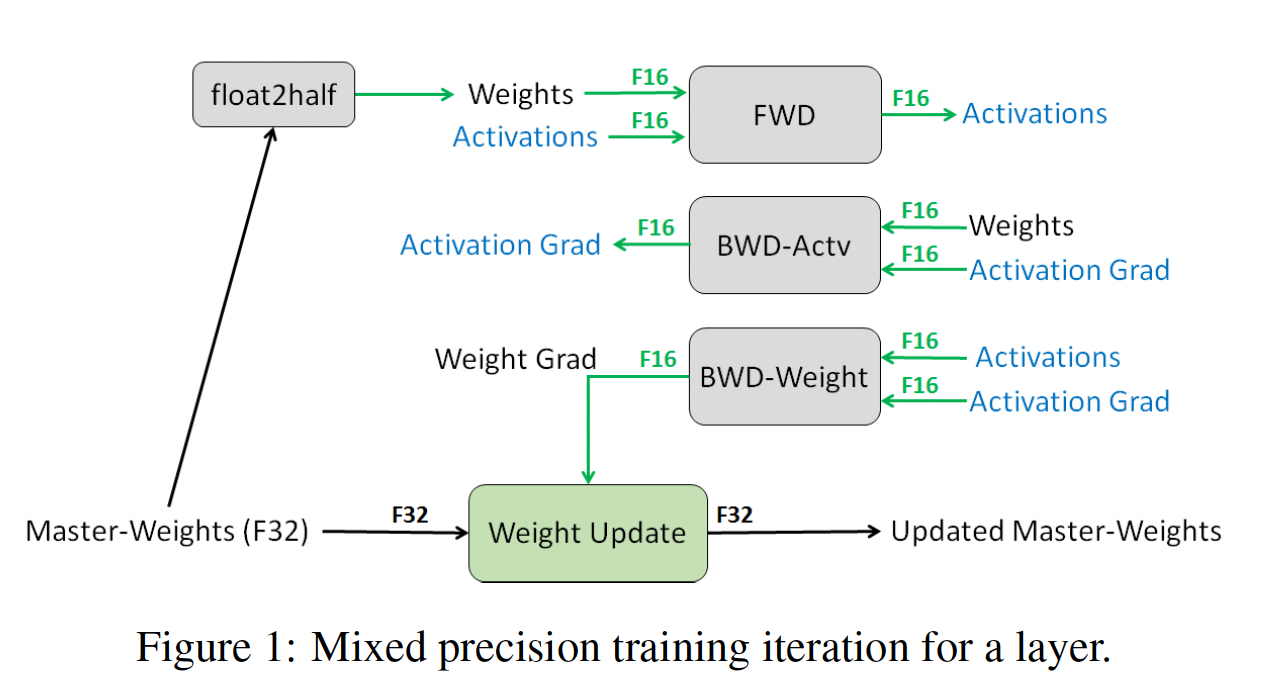
虽然
FP32 master weights的需求并非普遍存在,但有两个可能的原因解释为什么许多网络需要它:一个解释是
updates(weight gradients乘以学习率)变得太小而无法用FP16表示。FP16中任何magnitude小于Figure 2b所示,约5%的weight gradient values的exponents小于-24。在optimizer中,这些小的梯度与学习率相乘后会变成零,并对模型准确率产生不利影响。使用single-precision copy进行更新可以克服这个问题并恢复准确率。即,
weight updates绝对很小,导致updates变成零。另一个解释是
weight value与weight update的比率非常大。在这种情况下,即使weight update可以用FP16来表示,当加法操作将weight update右移从而将binary point与weights对齐时,weight update仍然可能变成零。当normalized weight value的magnitude比weight update的magnitude大至少2048倍时,这种情况可能发生。由于FP16有10-bit尾数,implicit bit必须右移11位或更多位才可能创建零(在某些情况下,rounding可以恢复该值)。在比率大于2048的情况下,implicit bit将右移12位或更多位。这将导致weight update变成无法恢复的零。更大的比率将对de-normalized数字产生这种效应。同样,这种效应可以通过在FP32中计算weight update来抵消。即,
weight updates相对weight很小,导致训练效率很低(即,每个step中,权重的变化幅度非常小)。
为了说明权重的
FP32 master copy的必要性,我们使用了Mandarin语音模型在约800小时的语音数据上训练20 epochs。如Figure 2a所示,当在FP16 forward and backward passes之后更新FP32 master copy of weights时,我们匹配了FP32 training结果;而更新FP16 weights则导致80%的相对accuracy loss。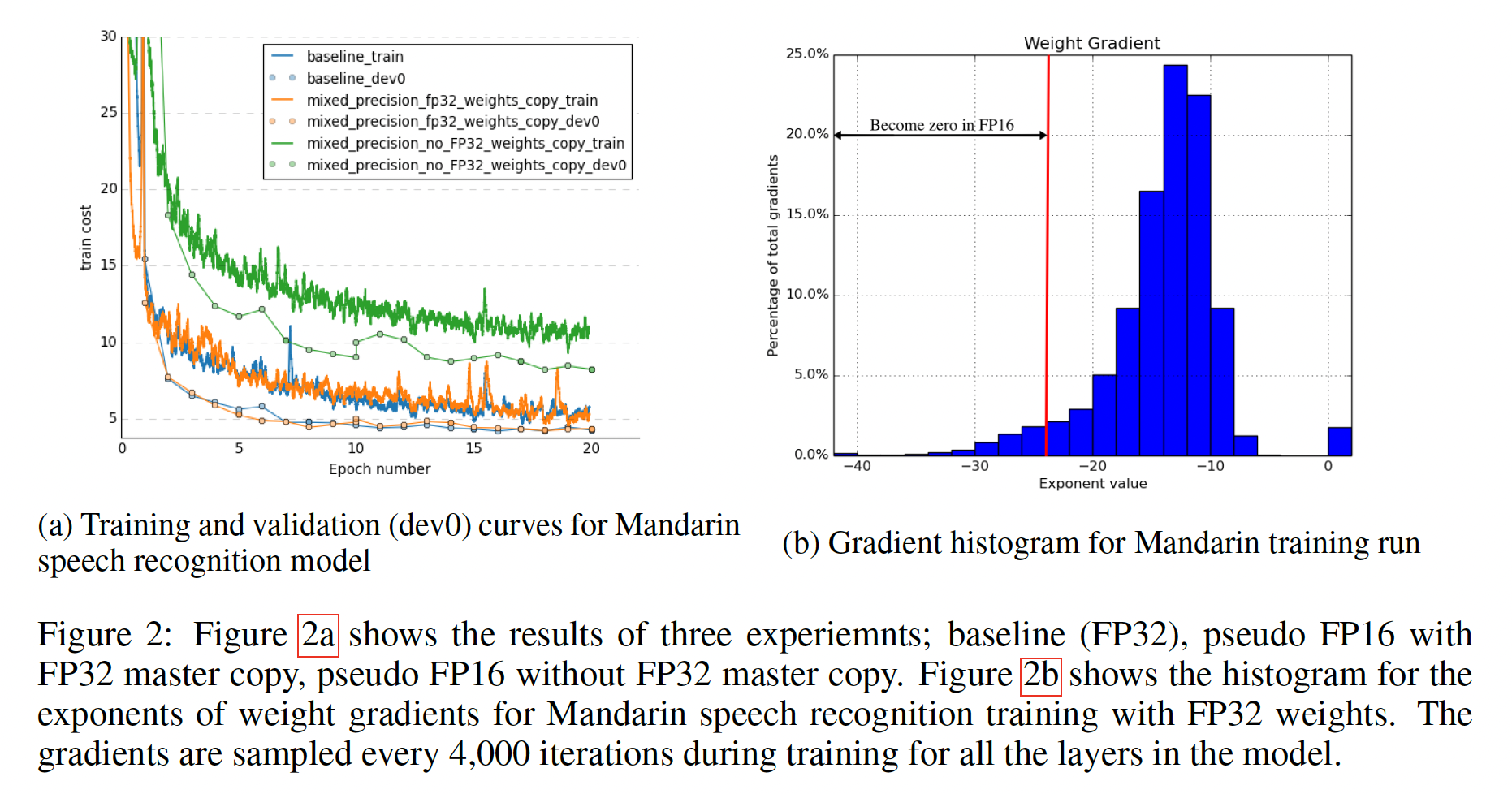
尽管与
single precision training相比,维护额外的权重副本将权重的内存需求增加了50%,但对整体内存使用的影响要小得多。 对于训练,内存消耗主要由activations引起,这是由于较大的batch size、以及保存每层的activations从而在反向传播中重用。 由于activations也以半精度格式存储,所以整体内存消耗约减半。作者这里并未给出数据来说明。
1.1.2 Loss Scaling
FP16 exponent将normalized value exponents范围有偏地居中到[-14,15],而实际梯度值往往以小magnitudes(negative exponents)为主。例如,考虑Figure 3,显示了在FP32训练Multibox SSD检测器网络过程中收集的所有层的activation gradient values的直方图。注意,FP16可表示范围的大部分未被使用,而许多值低于最小可表示范围并变为零。scaling up梯度将使它们占用更多的可表示范围,并保留一些值(如果不scaling up,这些值将会因为零而丢失)。不缩放梯度时,该特定网络会发散;但将其缩放
8倍(对exponents增加3)足以匹配FP32 training达到的准确率。这表明,在magnitude上小于activation gradient values对此模型的训练无关,但magnitude的activation gradient values很重要。由于学习率通常很小,因此
activation gradient values乘以学习率仍然可能小于Weight Update采用FP32,因此不会变为零。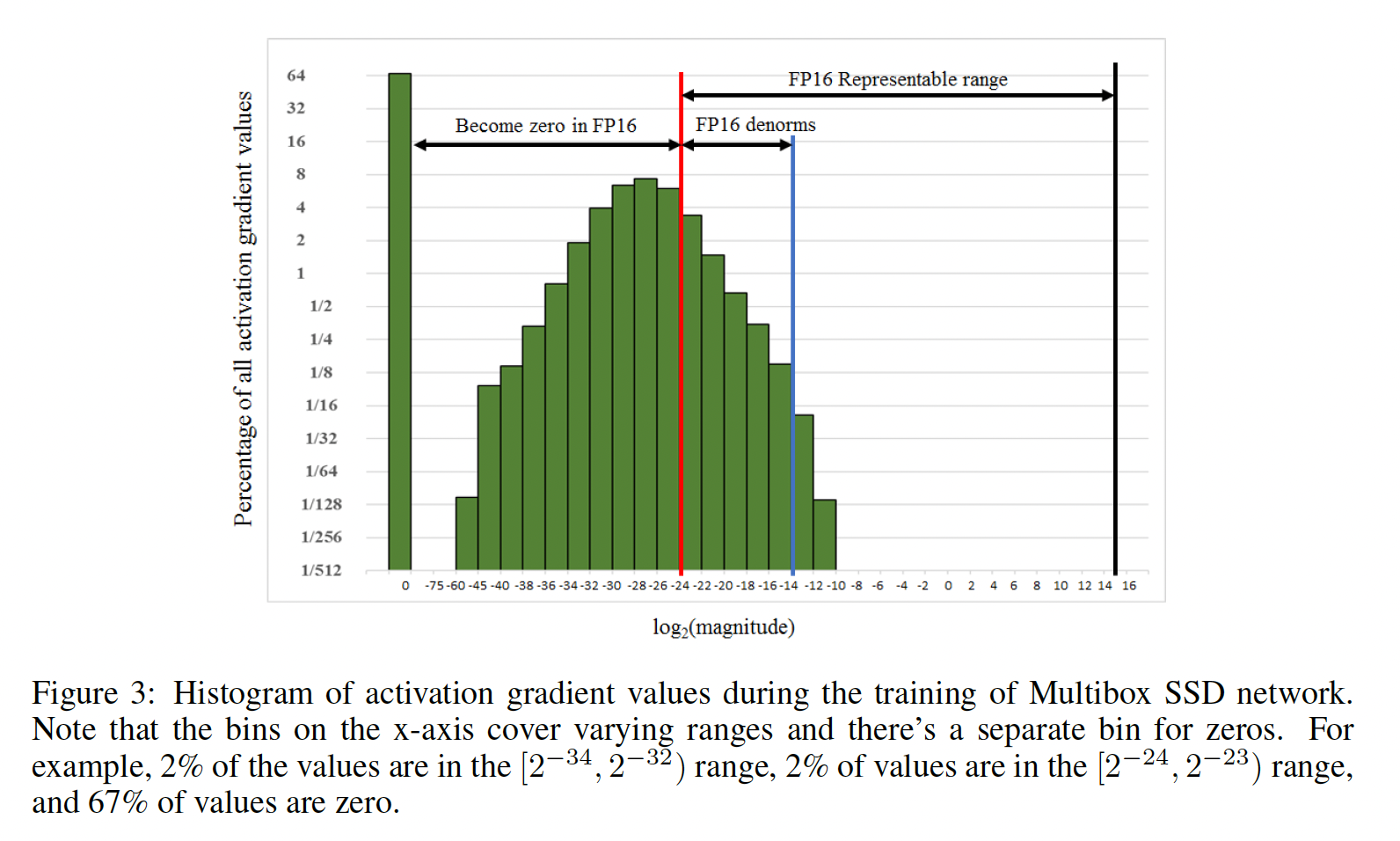
将
gradient values移至FP16可表示范围的一种有效方法是:在开始反向传播之前,缩放在前向传播中计算的loss value。通过链式法则,反向传播将确保所有梯度值被缩放相同的量。这在反向传播期间不需要额外的操作,并使相关的梯度值不会变成零。在权重更新之前,必须
unscale权重梯度,从而保持weight update magnitudes与FP32 training相同。最简单的方法是:在反向传播结束之后、但在梯度裁剪或任何其他与梯度相关的计算之前进行unscale,从而确保不需要调整任何超参数(如梯度裁剪阈值、weight decay等)。虽然可以通过缩小学习率来间接地缩放梯度,但是梯度裁剪阈值、
weight decay等等方法的超参数也需要相应地缩放。loss scaling factor有几种选择。最简单的一种是选择一个常量的scaling factor。我们用8到32K的scaling factor训练了各种网络(许多网络不需要scaling factor)。可以经验性地选择一个常量scaling factor,或者如果有梯度统计信息,可以直接选择一个scaling factor使其与maximum absolute gradient value的乘积低于65,504(FP16中可表示的最大值)。只要不在反向传播期间导致数值溢出,选择一个大的
scaling factor就没有坏处。数值溢出会导致weight gradients中出现无穷大和NaN,在权重更新后会不可逆地破坏权重。请注意,数值溢出可以通过检查计算到的weight gradients(例如在unscale weight gradient values的时候)来有效检测。一种解决方法是:在检测到数值溢出时跳过weight update,直接进入下一次迭代。
1.1.3 算术精度
在很大程度上,神经网络的算术分为三类:向量点积、
reductions、以及point-wise操作。这些算术类别在reduced precision算术方面受益于不同的处理。为了保持模型准确率,我们发现一些网络要求
FP16 vector dot-product从而累积partial products到FP32值,然后在写入内存前将其转换为FP16。如果不这样累积到FP32,一些FP16模型的准确率无法匹配baseline模型。而先前的GPU只支持FP16 multiply-add操作,而NVIDIA Volta GPU引入了Tensor Core,可以将FP16的 输入矩阵相乘并累积乘积结果到FP16 output或FP32 output。大型的
reductions(如向量元素之和)应在FP32中进行。这种reductions主要出现在batch-normalization layers(累积统计信息)和softmax layers。在我们的实现中,这两种layer类型仍从内存读取和写入FP16张量,而在FP32中执行算术运算。这并没有减慢训练过程,因为这些layers受内存带宽限制,而对于算术速度不敏感。point-wise操作(如非线性激活函数、element-wise矩阵乘法)受内存带宽限制。由于算术精度不影响这些操作的速度,可以使用FP16或FP32。
1.2 实验
略(参考原始论文)。
二、Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference[2017] [粗读]
论文:
《Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference》
论文是关于量化 CNN 模型的,这里仅做粗读,仅关注核心算法。
Introduction:略(参考原始论文)。相关工作:略(参考原始论文)。
2.1 Quantized Inference
2.1.1 量化方案
在这一节中,我们描述了通用的量化方案,也就是两种类型数值之间的对应关系:
bit representation of values(这个整数记为"quantized value")、以及它们作为数学的实数的解释(对应的实数记为"real value")。我们的量化方案在推理时只使用整数算术实现,在训练时使用浮点算术实现,两种implementations高度对应。我们首先数学上严格定义量化方案,然后分别采用该方案用于integer-arithmetic inference和floating-point training。floating-point training类似于量化感知训练Quantization Aware Training,即在训练阶段就应用 “模拟” 量化操作,从而降低integer-arithmetic inference的量化误差。我们量化方案的一个基本要求是,它允许只使用整数算术操作对
quantized values进行所有算术运算的有效实现(我们避免需要lookup tables的实现,因为它们往往比在SIMD硬件上进行纯算术运算表现更差)。这相当于要求量化方案是整数其中:
常数
"scale")是一个任意的正实数。它通常以软件中的浮点数形式表示,类似于实数常数
"zero-point")与quantized valuequantized valuequantized value精确地表示。这一要求的动机是,高效实现的神经网络算子通常需要对数组进行zero-padding。
这个公式是我们的量化方案,常数
quantization parameters)。我们的量化方案对每个activations array内的所有值、以及weights array内的所有值使用单组量化参数,即:不同的array使用独立的量化参数。对于
8-bit量化,8-bit整数(对于B-bit量化,B-bit整数)。一些数组(通常是bias vectors)被量化为32-bit整数,参见后续内容。到目前为止的讨论被总结在以下的
quantized buffer数据结构中,神经网络中的每个activations array和weights array都有这样一个buffer实例。我们使用C++语法是因为它可以明确地表达类型:xxxxxxxxxxtemplate<typename QType> // e.g. QType=uint8struct QuantizedBuffer {vector<QType> q; // the quantized valuesfloat S; // the scaleQType Z; // the zero-point};
2.1.2 仅整数算术的矩阵乘法
我们现在考虑如何仅使用整数算术进行推理,也就是如何使用方程
quantized-values运算,以及后者如何设计为仅包含整数算术,即使scaling参数考虑两个
quantized矩阵为从矩阵乘法的定义,我们有:
这可以重写为:
其中乘数
quantization scales其中:其中
归一化的乘数
int16或int32)。例如,如果使用int32的整数乘法,表示int32值。由于30-bit的相对精度。因此,乘以fixed-point multiplication)。同时,乘以
bit-shift),尽管需要具有正确的四舍五入(round-to-nearest)行为,我们在附录B中讨论这个问题。
2.1.3 高效处理 ZeroPoint
为了在不执行
16-bit整数的情况下,有效地实现公式其中:
每个
上式的剩余成本几乎全部集中在核心的整数矩阵乘法累加上:
这需要
的确,
zero-points都能以很小的开销处理,除了core integer matrix multiplication accumulation,因为我们在任何其他zero-points-free方案中都必须计算它。这仅仅改善了减法操作,而没有改善乘法操作。
原始方法中,对于
但是,对于乘法操作,二者之间并未改善。
2.1.4 典型 fused layer 的实现
我们继续前面的讨论,但现在显式地定义所有涉及的量(
quantities)的数据类型,并修改quantized的矩阵乘法,从而直接将bias-addition和activation function evaluation合并到其中。这样将整个layer融合成单个操作而不仅是一个优化。由于我们必须在推理代码中重现训练中使用的相同算术,推理代码中的fused operators的粒度(接受8-bit quantized input并产生8-bit quantized output)必须与训练图中"fake quantization" operators的placement相匹配。对于
ARM和x86 CPU架构,我们使用gemmlowp库(《gemmlowp: a small self-contained low-precision gemm library》),其GemmWithOutputPipeline入口点支持我们现在描述的fused operations。General Matrix Multiplication: GEMM:通用矩阵乘法。我们将
activations。权重和activations均为uint8类型(我们也可以等效地选择int8,适当修改zero-points)。uint8值的乘积的累加需要32-bit accumulator,我们为accumulator选择带符号类型,原因很快就会变清楚。为了得到
quantized bias-addition(将int32 bias添加到int32 accumulator上),bias-vector被量化为:使用
int32作为其量化数据类型。使用
0作为其quantization zero-point其
quantization scaleaccumulators的相同,即weights scale和input activations scale的乘积:
尽管
bias-vectors被量化为32-bit值,但它们只占神经网络参数的很小一部分。此外,对bias vectors使用更高精度满足了一个真正的需求:由于每个bias-vector entry被添加到许多output activations中,bias-vector中的任何量化误差往往表现为一个overall bias(即,均值不为零的误差项),这必须避免以保持端到端的神经网络准确性。即,对于任何样本
bias-vector都添加到它的output activation上,因此bias-vector对所有样本都产生了影响。对
int32 accumulator的最终值,还剩下三件事要做:scale down到final scale,这个final scale被8-bit output activations所使用。cast down到unit8。应用
activation function生成final 8-bit output activation。
下采样对应于乘数
rounding bit-shift组成。之后,我们执行cast到uint8,饱和到[0,255]范围。我们仅仅关注
clamps类型的激活函数,例如ReLU、ReLU6。数学函数在附录A.1中讨论,目前我们不会将它们融合到这种层中。因此,我们fused activation functions唯一需要做的就是进一步将uint8值截断到[0,255]的某个子区间,然后存储final uint8 output activation。实际上,quantized training process(参考下一节)倾向于学习使用整个output uint8区间[0,255],以致activation function不再起任何作用,其效果被归因于截断到区间[0, 255](由于cast到unit8所隐含的)。
2.2 Training with simulated quantization
在大模型时代,通常很少采用
simulated quantization的训练,而是直接训练一个大模型,然后再进行post-training量化。
训练
quantized networks的常见方法是:用浮点进行训练,然后量化所得到的权重(有时伴随额外post-quantization training从而进行微调)。我们发现,这种方法对具有相当表达能力的大型模型效果足够好,但对小型模型会导致明显的准确率下降。simple post-training quantization的常见失败模式包括:1):不同output channels的权重范围差异很大(大于100倍)。注意:前面章节中规定,同一层的所有通道必须量化到相同分辨率;这会导致权重范围较小的通道中,权重的相对误差更大。2):outlier weight values,这些异常值使得量化后所有的非异常值的权重降低了精确性。
我们提出了一种在训练的前向传播中模拟量化效应(
quantization effects)的方法。反向传播仍然照常进行,所有权重和bias以浮点存储,以便可以轻易地略微调整。但是,前向传播模拟quantized inference(因为quantized inference发生在推理引擎中),通过如下方式:以浮点算法实现我们前面介绍的量化方案中的rounding behavior。权重在与
input执行卷积之前被量化。如果layer使用batch normalization,则在量化之前,batch normalization参数被 “折叠”到权重中。activations在这样的时点上被量化:在推理期间activations被量化的点。例如:在activation function应用于卷积层或全连接层输出之后、或在像ResNet中那样多个层的输出相加或拼接的bypass connection之后。
对于每一层,
quantization由quantization levels数量、以及clamping range的参数化,并通过point-wise地应用下面定义的量化函数其中:
quantization levels数量;在我们的实验中,
8-bit量化时即,在原始的神经网络中插入这些特定的
fake quantization layer。
2.2.1 学习 quantization ranges
weight quantization与activation quantization的quantization ranges的处理不同:对于权重,基本思想是:简单地设置
int8值,取值范围仅仅在[-127, 127]并且不会取值为-128,因为这enable了一个重要的optimization opportunity(更多细节见附录B)。对于
activations,ranges取决于网络输入。为了估计ranges,我们在训练期间收集activations上的[a; b]范围,然后通过指数移动平均(exponential moving averages: EMA)聚合它们,平滑参数接近1,以便observed ranges在数千步训练中平滑。鉴于在ranges快速变化时,EMA更新activation ranges有明显延迟,我们发现在训练开始时完全禁用activation quantization很有用(例如前50K步到2M步)。这使网络进入更稳定状态,其中activation quantization ranges不会排除values的重要部分。这类似于
Batch Normalization的思想。在训练中自动更新activation ranges。
在两种情况下,都会调整
[a; b]的边界,以便值0.0在量化后可以精确表示为整数quantization parameters映射到方程scalezero-point下面我们假设神经网络的计算被捕获为
TensorFlow graph,然后描述simulated quantization。典型的工作流程在Algorithm 1中描述。通过fusing and removing operations的inference graph的优化,超出了本文范围。用于graph modifications的源码(插入fake quantization操作、创建和优化inference graph)、以及low bit inference engine已在《Tensorflow quantized training support》中通过TensorFlow contributions开源。公式
12为:
Figure 1.1 a and b说明了一个简单卷积层量化前后的TensorFlow graph。Figure C.3中,更复杂的带bypass connection的卷积的说明,可以在Figure C.4中找到。请注意,
bias没有被量化,因为在推理过程中它们表示为32-bit整数,范围和精度远高于8-bit weights and activations。此外,用于,bias的量化参数从权重和激活的量化参数推导出来。使用
《Tensorflow quantized training support》的典型TensorFlow代码示例如下:xxxxxxxxxxfrom tf.contrib.quantize import quantize_graph as qgg = tf.Graph()with g.as_default():output = ...total_loss = ...optimizer = ...train_tensor = ...if is_training:quantized_graph = qg.create_training_graph(g)else:quantized_graph = qg.create_eval_graph(g)# Train or evaluate quantized_graph.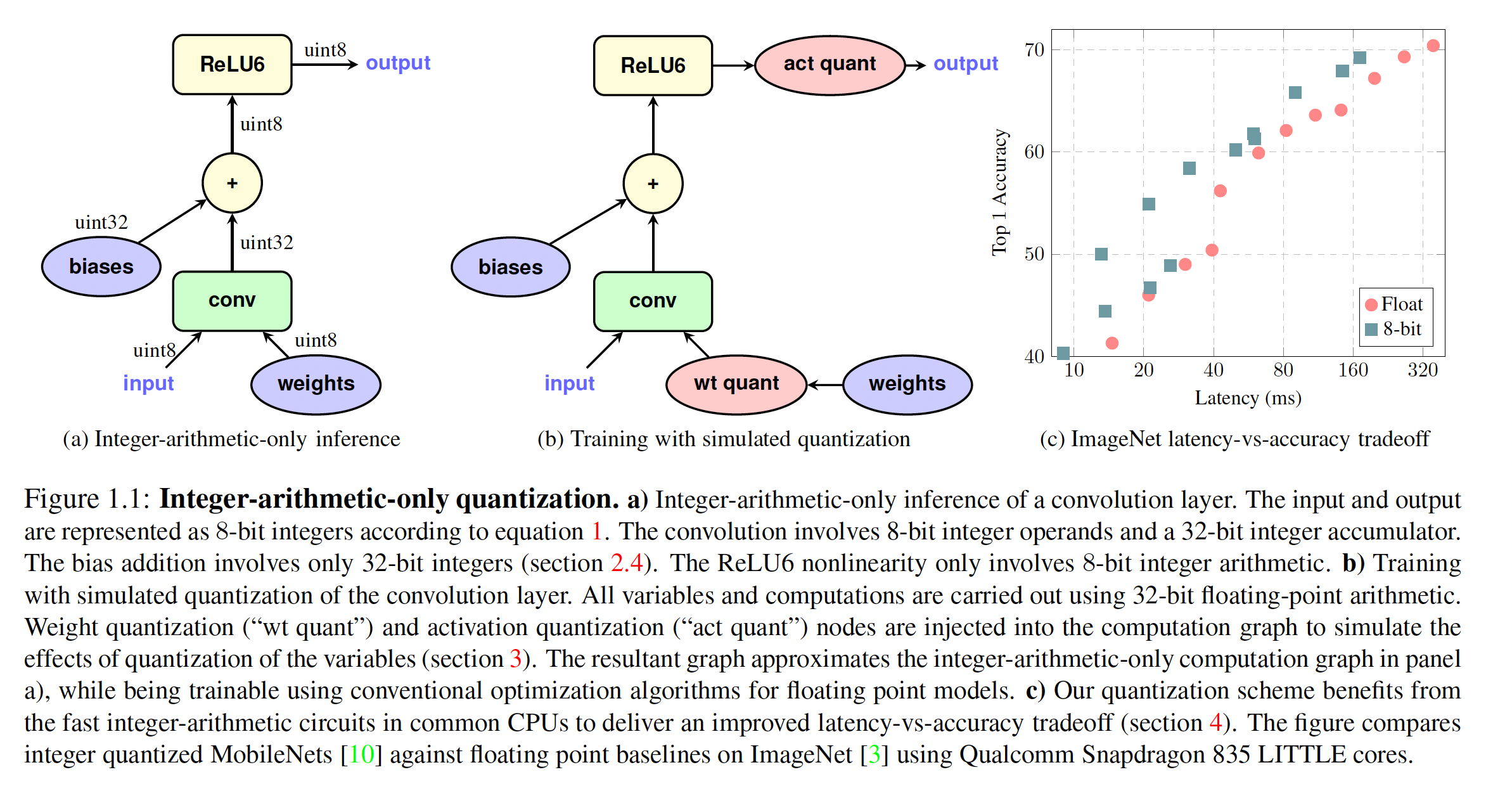
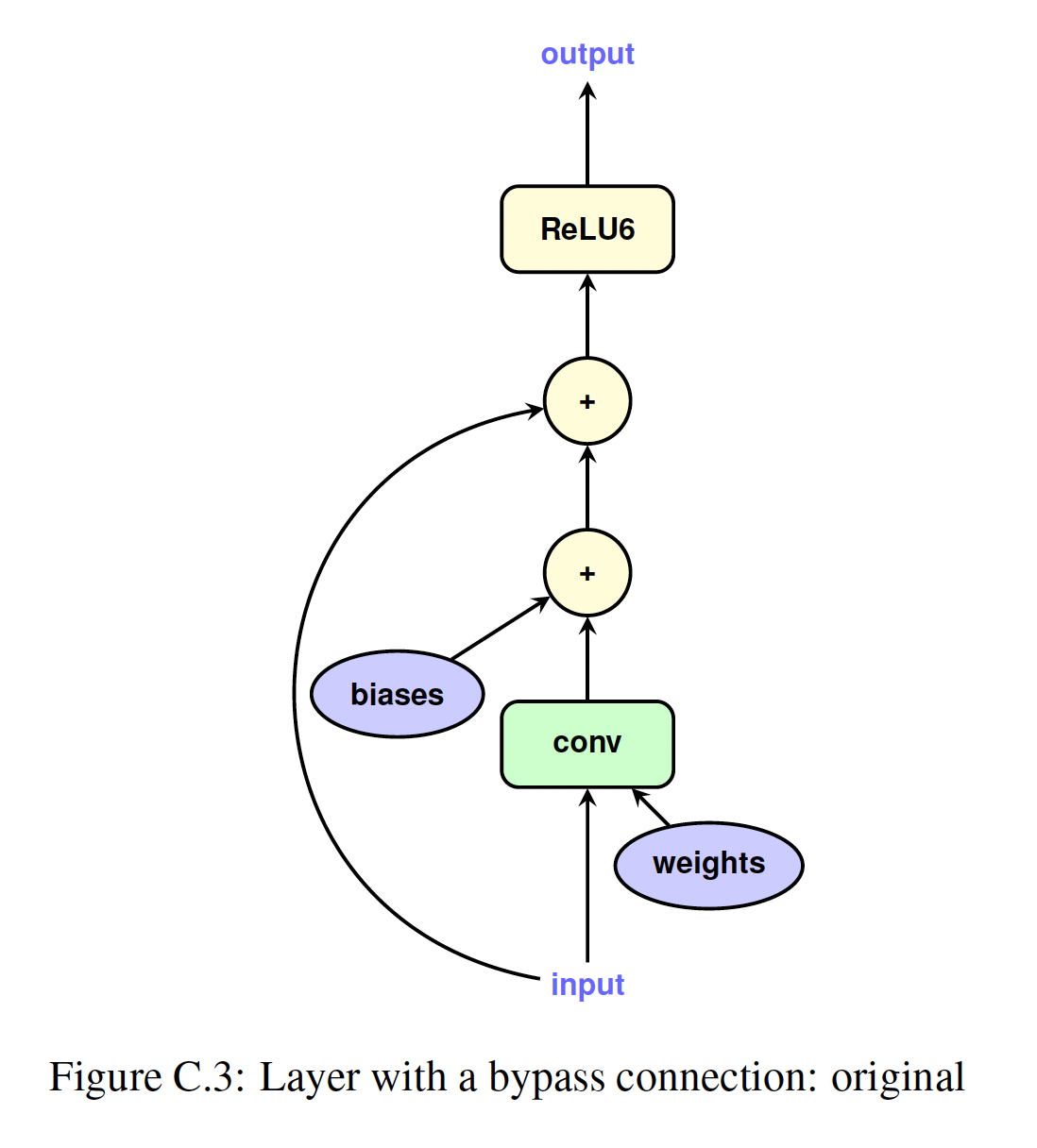
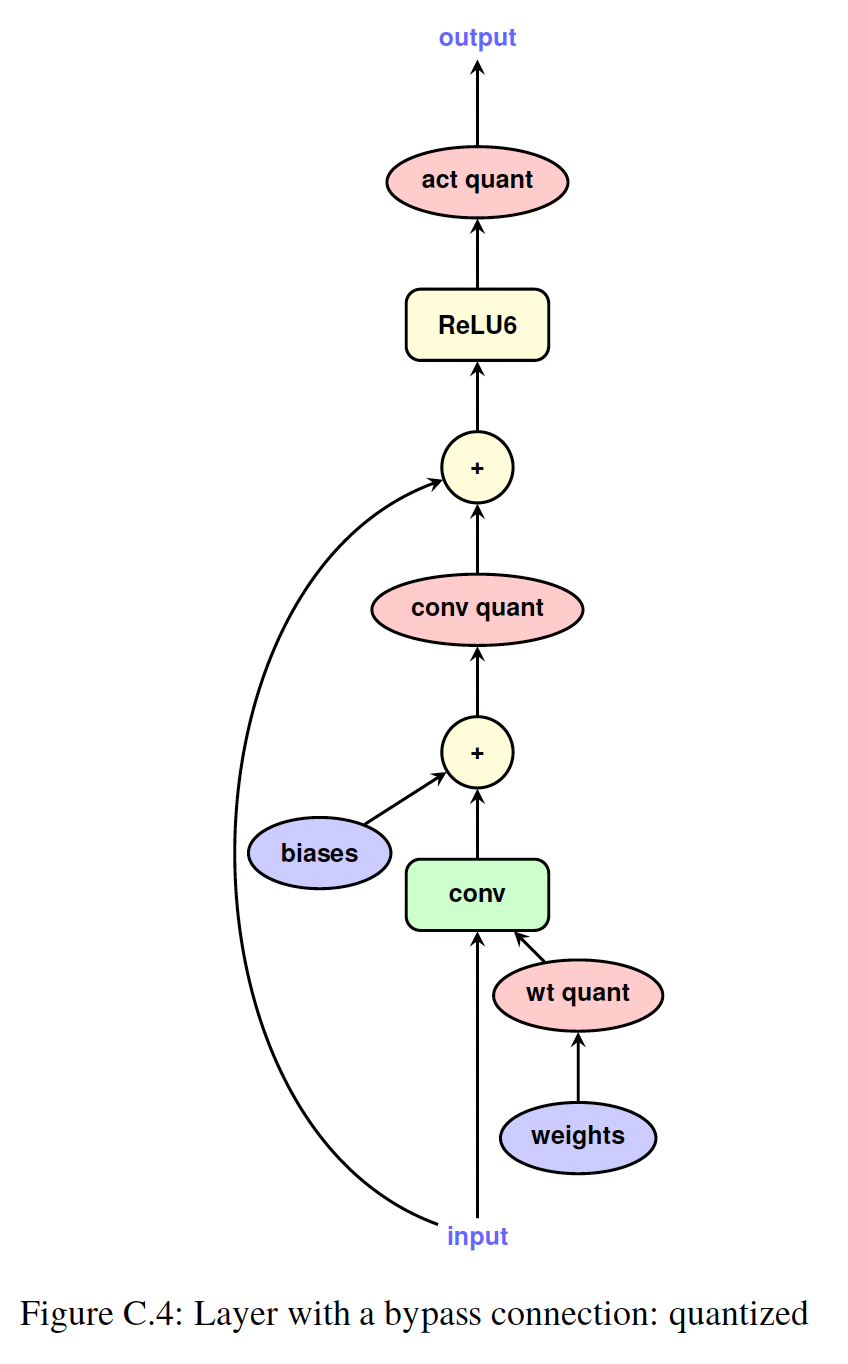
2.2.2 Batch normalization folding
对于使用
batch normalization的模型,存在额外复杂性:training graph中batch normalization是单独的操作块,而inference graph中batch normalization参数 “折叠” 到卷积层或全连接层的权重和bias中,从而提高效率。为了准确模拟量化效应,我们需要模拟这种折叠,并在权重被batch normalization parameters缩放后再来量化权重。我们采用以下方法:其中:
batch normalization的scale参数。convolution results的batch内方差的移动平均估计。
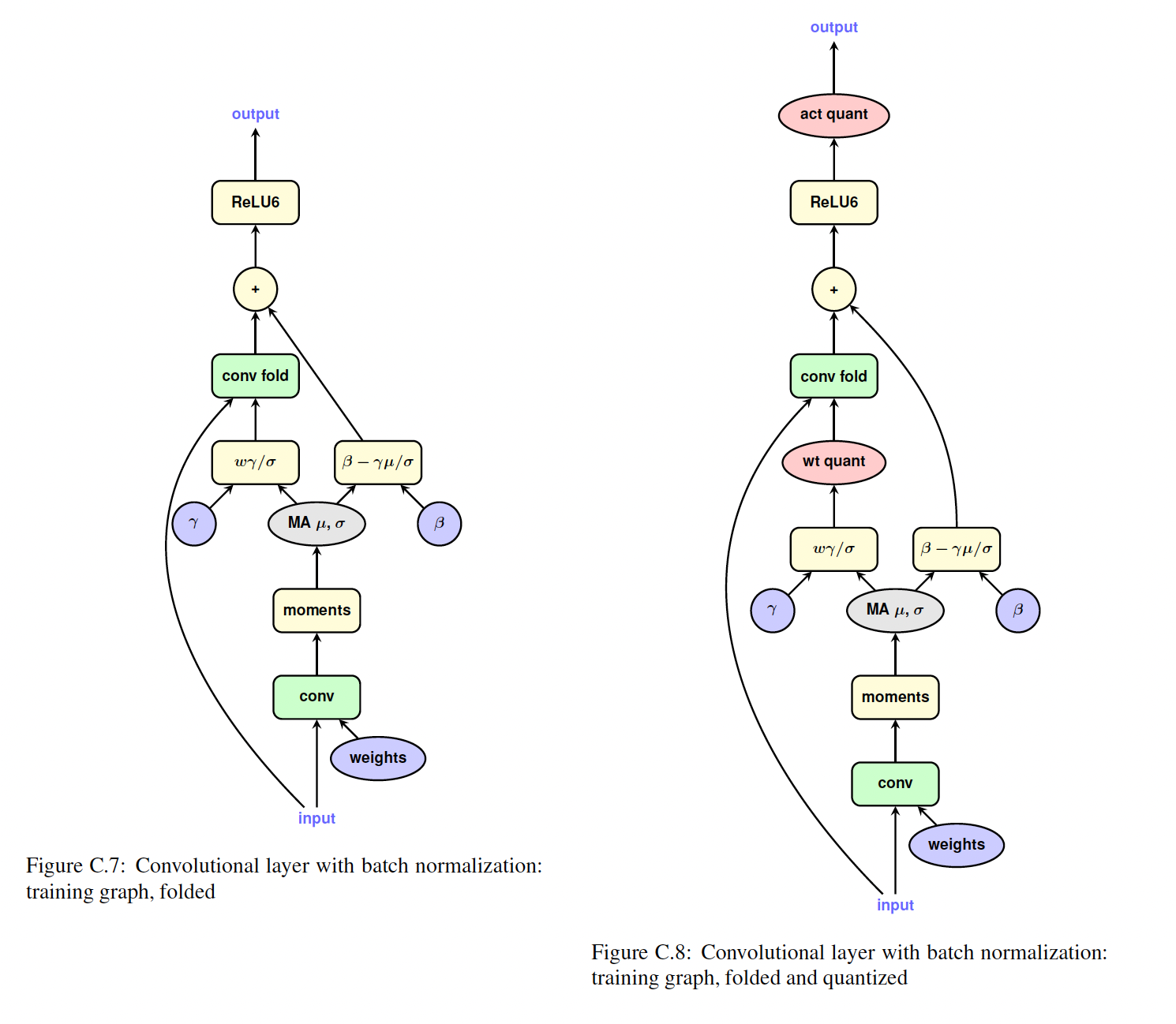
折叠后,
batch-normalized convolutional layer简化为Figure 1.1a中所示的简单卷积层,具有被折叠的权重bias。因此,相同的配方也适用于Figure 1.1b。附录中可以查阅batch-normalized convolutional layer(Figure C.5)、相应的inference graph(Figure C.6)、batch-norm folding后的训练图(Figure C.7)以及folding and quantization后的训练图(Figure C.8)。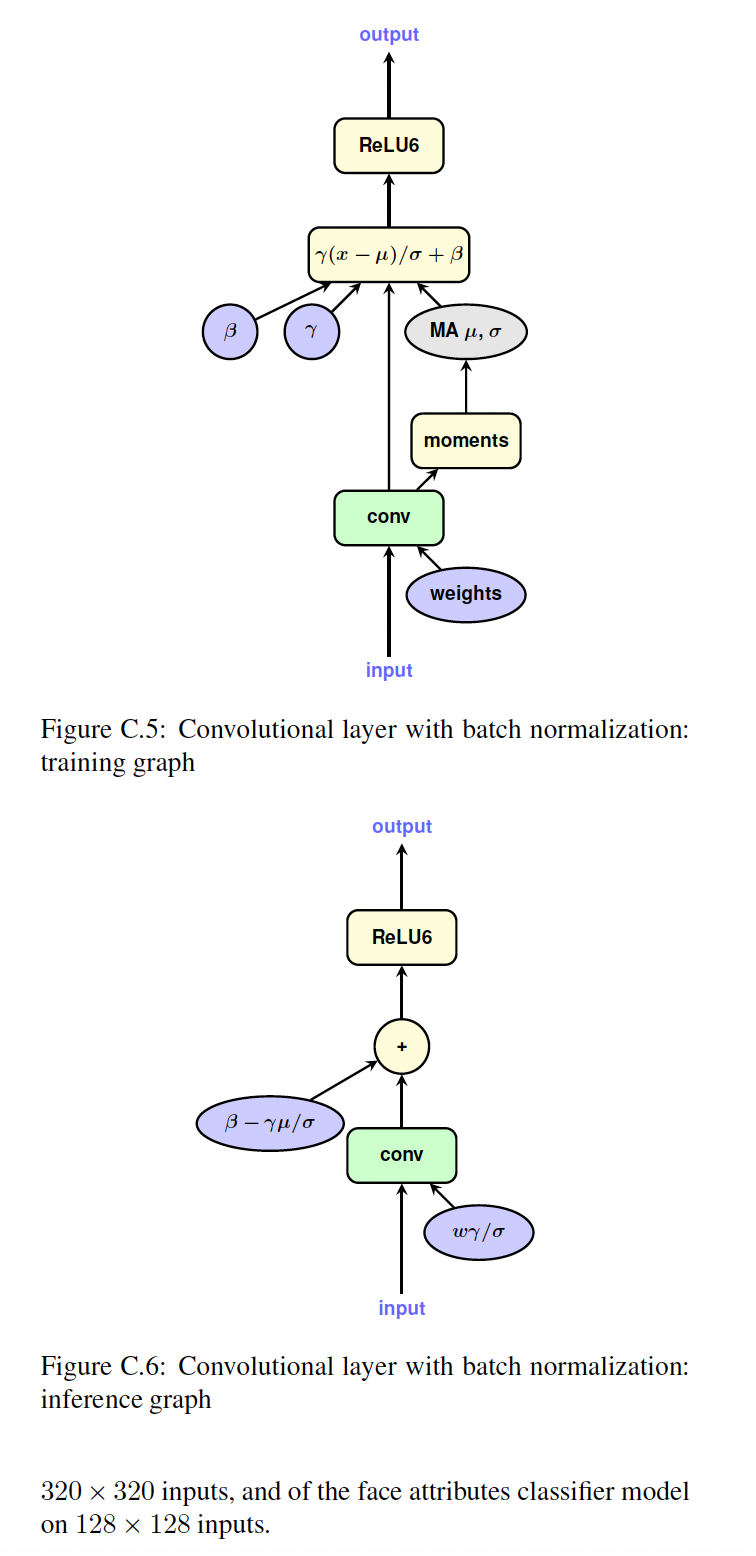
2.3 实验
略(参考原始论文)。
三、LLM.int8()[2022]
论文:
《LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale》
大型
pretrained语言模型在NLP中被广泛采用,但需要大量内存进行推理。对于超过6.7B参数的大型transformer语言模型,前馈层(feed-forward layer)和注意力投影层(attention projection layer)及其矩阵乘法操作占据了95%的参数和65-85%的所有计算(《High performance natural language processing》)。减小参数大小的一种方法是将其量化为更少的比特并使用低位精度(low-bit-precision)的矩阵乘法。考虑到这一目标,人们已经开发了transformer的8-bit量化方法。虽然这些方法减少了内存使用,但它们降低了性能,通常需要在训练后进一步tuning quantization,并且只在少于350M参数的模型上进行了研究。低于350M参数时性能无损的量化理解得不够好,十亿参数级的量化仍是一个开放性挑战。在本文中,我们提出了第一个不降低性能的十亿参数级
Int8量化过程。我们的过程使得加载一个具有16-bit或32-bit参数的175B参数的transformer,将前馈层和注意力投影层转换为8-bit,并立即用于推理而不降低任何性能。我们通过解决两个关键挑战实现了这一结果:大于
1B参数时需要更高的量化精度(quantization precision)。需要明确表示稀疏的但系统性的大幅值的异常值特征(
sparse but systematic large magnitude outlier features),在所有的transformer层(从6.7B参数规模开始)中,这些特征一旦出现就会破坏量化精度。一旦这些异常值特征出现,C4 evaluation perplexity以及zero-shot accuracy就会反映出这种精度损失(loss of precision),如Figure 1所示。

我们证明,通过我们方法的第一部分向量化量化(
vector-wise quantization),可以在高达2.7B参数的规模下保持性能。对于向量化量化,矩阵乘法可以看作是行向量序列和列向量序列的独立内积序列。因此,我们可以为每个内积使用单独的量化归一化常数(quantization normalization constant)来提高量化精度。我们可以通过在执行下一个操作之前用列归一化常数和行归一化常数的外积对矩阵乘法的输出进行反归一化(denormalizing)来恢复矩阵乘法的输出。为了在不降低性能的情况下扩展到超过
6.7B的参数,理解推理过程中隐状态(隐状态就是activation)feature dimensions中的极端异常值的出现至关重要。为此,我们提供了一个新的描述性分析,该分析显示:在将
transformer扩展到6B参数时,所有transformer层中大约25%首先出现了幅度高达其他维度20倍的大特征(large features),然后这些大特征逐渐传播到其他层。在大约
6.7B参数时,发生了一个phase shift,所有transformer层、以及75%的所有sequence dimensions都受到极端幅度的特征(extreme magnitude features)的影响。这些异常值高度地系统化(systematic):在6.7B规模下,每个序列有150,000个异常值,但它们集中在整个transformer中的仅6个feature dimensions中。将这些异常
feature dimensions设置为零会使top-1 attention softmax概率质量降低20%以上,并使validation perplexity退化600-1000%,尽管它们只占所有输入特征的约0.1%。相比之下,删除相同数量的随机特征会最大降低0.3%的概率质量,并退化约0.1%的困惑度(perplexity)。
给定一个文本序列,
sequence维度表示token id的维度,feature表示embedding或activation的维度。上述描述的含义是:在
6B模型,有25%的层(在
6.7B模型,所有的层出现了异常值;沿着token id的方向,有75%的位置出现了异常值(embedding/activation的方向,有6个位置出现了异常值(
写成矩阵的形式:
为了支持这样极端异常值的有效量化,我们开发了混合精度分解(
mixed-precision decomposition),即我们方法的第二部分。 我们对异常feature dimensions执行16-bit矩阵乘法、对其余99.9%的维度执行8-bit矩阵乘法。我们将向量化量化、以及混合精度分解的组合命名为LLM.int8()。 我们证明,通过使用LLM.int8(),我们可以在具有多达175B参数的LLM上进行推理,而不降低任何性能。我们的方法不仅为这些异常值对模型性能的影响提供了新的见解,而且还首次使非常大的模型(例如OPT-175B/BLOOM)能够在具有消费级GPU的单服务器上使用。虽然我们的工作重点是在不降低性能的情况下使大型语言模型可访问,但我们在附录D中还展示了我们为大型模型(如BLOOM-176B)维持端到端inference runtime性能,并为大于或等于6.7B参数的GPT-3模型提供了适度的矩阵乘法速度提升。我们开源了我们的软件,并发布了Hugging Face Transformers集成,使我们的方法可用于Hugging Face Models托管的所有具有线性层的模型。可以看到,
LLM.int8()仅在较大的模型(模型规模大于6.7B)时才会加速推断;在更小的模型时,推断速度反而更慢(相比较于原始的FP16)。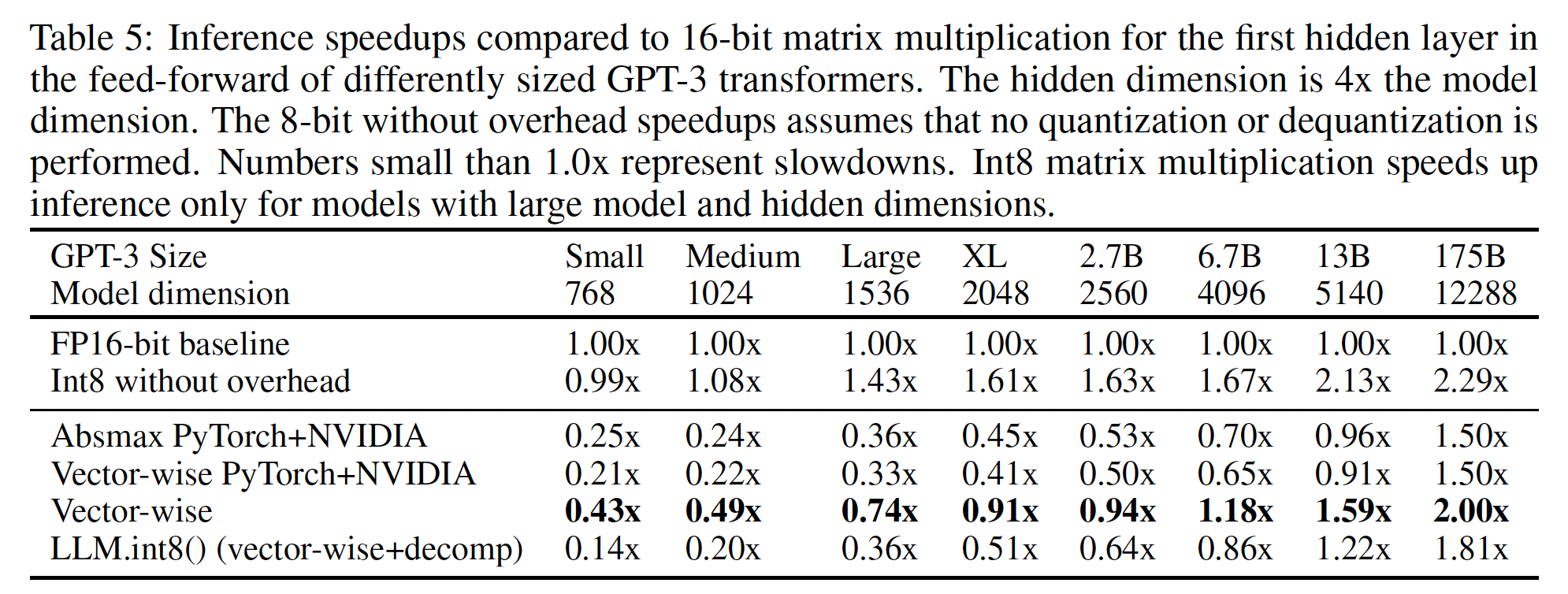
相关工作:下面列出了
quantization data types、以及quantization of transformers有密切相关的工作。附录B提供了有关quantization of convolutional networks的更多相关工作。8-bit Data Types:我们的工作研究围绕Int8数据类型的量化技术,因为它目前是GPU支持的唯一8-bit数据类型。其他常见的数据类型是定点8-bit数据类型或浮点8-bit数据类型(floating point 8-bit: FP8)。这些数据类型通常有一个符号位(
sign bit) 、以及指数位(exponent bit)和小数位(fraction bit) 的不同组合。例如,这种数据类型的一个常见变体有5 bits指数、2 bits小数,并使用zeropoint scaling或者no scaling constants。由于这些数据类型对fraction只有2 bits,所以对大的幅值(large magnitude)有很大误差,但可以为小的幅值提供高精度。《F8net: Fixed-point 8-bit only multiplication for network quantization》提供了出色的分析,关于对具有特定标准差的输入,在何时某些fixed point exponent/fraction bit widths是最佳的。我们认为FP8数据类型与Int8数据类型相比提供了优异的性能,但当前GPU和TPU都不支持此数据类型。语言模型中的异常值特征(
Outlier Features):语言模型中大幅值异常值特征(large magnitude outlier features)的研究已经存在。先前的工作证明了
transformer中异常值出现与layer normalization以及token frequency distribution的理论关系(《Representation degeneration problem in training natural language generation models》)。类似地,
《Bert busters: Outlier dimensions that disrupt transformers》将BERT模型族中异常值的出现归因于LayerNorm。《Outliers dimensions that disrupt transformers are driven by frequency》在经验上表明异常值的出现与训练分布中tokens的频率有关。
我们通过展示自回归模型的规模与这些异常值特征的
emergent properties之间的关系,以及适当建模异常值对有效量化(effective quantization)的重要性,从而来进一步扩展这项工作。十亿规模
transformer的量化:与我们的工作相比,人们平行开发了两种方法:nuQmm(《nuqmm: Quantized matmul for efficient inference of large-scale generative language models》)、以及ZeroQuant(《Zeroquant: Efficient and affordable post-training quantization for large-scale transformers》)。两者使用相同的量化方案:分组向量化量化(group-wise quantization),其量化归一化常数粒度比向量量化更细。这种方案提供了更高的量化精度,但也需要自定义的CUDA kernels。nuQmm和ZeroQuant旨在加速推理和减少内存占用,而我们则关注在8-bit内存占用下保留预测性能。nuQmm和ZeroQuant评估的最大模型分别是2.7B和20B参数的transformer。ZeroQuant实现了20B模型的8-bit量化,同时保持性能没有衰退。我们展示了我们的方法允许高达176B参数的模型进行zero-degradation quantization。nuQmm和ZeroQuant表明,更细粒度的量化可以是大型模型量化的有效手段。这些方法与LLM.int8()是互补的。
另一个平行工作是
GLM-130B,它使用我们工作的见解实现zero-degradation 8-bit quantization(《Glm-130b: An open bilingual pre-trained model》)。GLM-130B以8-bit weight storage进行完整的16-bit精度的矩阵乘法。相比之下,
LLM.int8()采用8-bit的矩阵乘法。
3.1 背景知识
在这项工作中,我们通过扩展
transformer模型将量化技术推向了极限。我们对两个问题感兴趣:在何种模型规模下量化技术会失败,以及为何量化技术会失败?
量化技术的失败与量化精度有何关系?
为了回答这些问题,我们研究了高精度非对称量化(
zeropoint quantization)和高精度对称量化(absolute maximum quantization)。虽然zeropoint quantization通过使用数据类型的full bit-range提供了高精度,但由于实际限制而很少使用它。absolute maximum quantization是最常用的技术。
3.1.1 8-bit 数据类型和量化
absmax量化通过将输入乘以8-bit范围[-127, 127]中。因此,对于FP16数据类型的输入矩阵Int8 absmax quantization由以下公式给出:其中:
zeropoint量化通过如下的方式将input distribution移动到full range [-127, 127]中:首先用normalized dynamic rangezeropointaffine transformation),任何输入张量都将使用数据类型的所有比特,从而减少非对称分布(asymmetric distributions)的量化错误。例如,对于ReLU输出,在absmax量化中,所有[-127, 0)的值都未被使用;而在zeropoint量化中,完整范围[-127,127]都被使用。zeropoint量化由以下等式给出:推导过程:假设
[-127, 127]之间。则可以采用仿射变换:然后根据
根据论文
《Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference》,zeropoint量化的形式为:因此:
逆量化为:
要在操作中使用
zeropoint量化,我们同时传入张量zeropoint16-bit整数操作之前,将zeropoint quantized数值如果没有
multiply_i16指令,如在GPU或TPU上,则需要展开:注意:结果是
32-bit整数。其中:
Int8精度计算,其余以Int16/32精度计算。因此,如果没有multiply_i16指令,zeropoint量化可能比较慢。在上述两种情况下,输出以
32-bit整数即:
具有
16-bit浮点输入和输出的Int8矩阵乘法:给定隐状态sequence dimensions、feature dimensions、16-bit浮点输入和输出的8-bit矩阵乘法如下:其中:
tensor-wise的量化常数:对于
absmax量化,它们分别为对于
zeropoint量化,它们分别为
absmax量化或zeropoint量化。
3.2 大规模的 Int8 矩阵乘法
使用每个张量一个
scaling constant(即,scaling constant)的量化方法的主要挑战是,单个异常值可以降低所有其他值的量化精度。因此,每个张量拥有多个scaling constant是可取的,比如block-wise constants(《8-bit optimizers via block-wise quantization》),这样异常值的影响就局限于每个block。我们通过使用向量化量化(vector-wise quantization)来改进row-wise quantization(《Fbgemm: Enabling high-performance low-precision deep learning inference》),其中row-wise quantization是最常见的blocking quantization方式之一,详细内容如下所述。为了处理超过
6.7B规模的所有transformer layers中出现的大幅值异常值特征(large magnitude outlier features),仅仅向量化量化是不够的。为此,我们开发了混合精度分解(mixed-precision decomposition),其中少量的大幅值的feature dimensions(large magnitude feature dimensions),占比约0.1%以16-bit精度来表示,而其他99.9%的值以8-bit相乘。由于大多数元素仍以低精度来表示,与16-bit相比,我们仍保留约50%的内存减少。例如,对于BLOOM-176B,我们将模型的内存占用降低了1.96倍。Figure 2显示了向量化量化和混合精度分解。LLM.int8()方法是absmax vector-wise quantization和混合精度分解的组合。注意:
activation(即,本文并没有理论指导,而是根据大模型的实验性分析从而得到的方法。
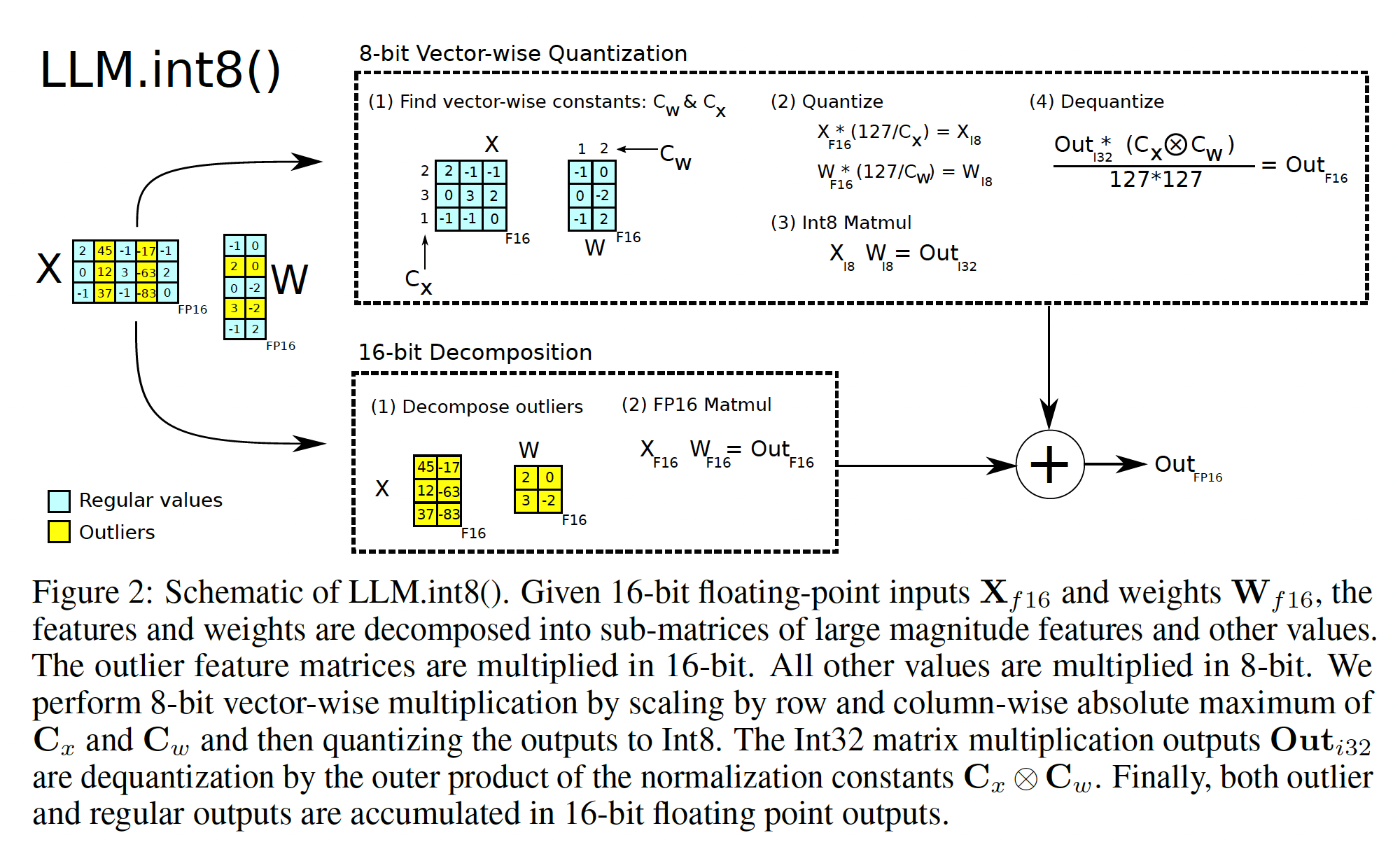
3.2.1 Vector-wise Quantization
增加矩阵乘法的
scaling constants的数量的一种方法是:将矩阵乘法视为独立内积的序列。给定隐状态scaling constantsdenormalize每个内积结果。对于整个矩阵乘法,这相当于通过外积denormalize,其中scaling constants和列scaling constants的矩阵乘法的完整方程如下:其中:
absmax量化。scaling constants矩阵。
我们将其称为矩阵乘法的向量化量化。
对于向量
3.2.2 LLM.int8() 的核心: Mixed-precision Decomposition
通过我们的分析,我们证明十亿级参数的
8-bit transformer的一个重大问题是,它们具有大幅值特征(列),这对transformer性能非常重要,需要高精度量化。但是,我们的最佳量化技术(即,向量化量化)对每个隐状态行进行量化,这对异常值特征(outlier features)无效。幸运的是,我们看到这些异常值特征在实践中非常稀疏且系统化,只占所有feature dimensions的约0.1%,因此允许我们开发一种新的分解技术,重点关注这些特定维度的高精度乘法。这段话的意思是,异常值是集中在输入
scaling constants会受到异常值的影响。我们发现,给定输入矩阵
row系统性地出现,但局限于特定的列。因此,我们为矩阵乘法提出混合精度分解,其中我们将包含异常值的列分离到集合transformer的performance degradation减少到接近零。使用爱因斯坦记号,其中所有索引都是上标,给定权重矩阵其中:
denormalization项。这种分离为
8-bit和16-bit允许异常值的高精度乘法,同时使用内存高效的矩阵乘法,其中包含8-bit权重值(在所有权重值中占比99.9%以上)。由于异常值的列对于高达13B参数的transformer不超过7(即,0.1%的额外内存。
3.2.3 实验设置
我们随着模型规模的增加来衡量量化方法的稳健性,规模达到
175B参数。关键问题不是某种量化方法对特定模型的表现如何,而是随着我们增加规模,这种方法的表现趋势如何。我们使用两种实验设置:
一种基于语言建模困惑度(
language modeling perplexity),我们发现这是一种高度稳健的指标,对quantization degradation非常敏感。我们使用此设置来比较不同的quantization baselines。对于语言建模设置,我们使用在
fairseq中预训练好的稠密的自回归transformer,参数范围在125M到13B之间。这些transformer在Books、English Wikipedia、CC-News、OpenWebText、CC-Stories、English CC100上进行了预训练。有关如何训练这些pretrained models的更多信息,请参阅《Efficient large scale language modeling with mixtures of experts》。为了评估
Int8 quantization后语言建模的degradation,我们在C4语料库的验证数据上评估8-bit transformer的困惑度。C4语料库是Common Crawl语料库的一个子集。我们使用NVIDIA A40 GPU进行评估。另外,我们在
OPT模型上评估zero-shot accuracy degradation,跨不同的下游任务,其中我们将我们的方法与16-bit baseline进行比较。为了测量
zero-shot性能的degradation,我们使用OPT模型,并在EleutherAI语言模型评估工具箱上对这些模型进行评估。
3.2.4 主要结果
在
C4语料上对125M到13B的Int8模型的语言建模困惑度的主要结果见Table 1。我们看到:随着模型规模的增加,
absmax、row-wise和zeropoint等等量化都失败了,2.7B参数后的模型性能低于较小的模型。zeropoint量化在超过6.7B参数后失败。在
13B规模,所有baseline方法的效果不如6.7B规模的模型。我们的方法
LLM.int8()是唯一保持困惑度的方法。因此,LLM.int8()是唯一具有良好缩放趋势的方法。
row-wise:即block-wise量化,将张量拆分为多个block,每个block拥有一个量化常数。倒数第三行(
Int8 absmax row-wise + decomposition)和Absmax LLM.int8()(vector-wise + decomp)的区别仅仅是:前者采用row-wise、后者采用vector-wise。最后两行的区别在于:前者采用
Absmax、后者采用Zeropoint。可以看到,Zeropoint相对于absmax的优势(第二行和第三行)消失了。原因见作者后面的讨论。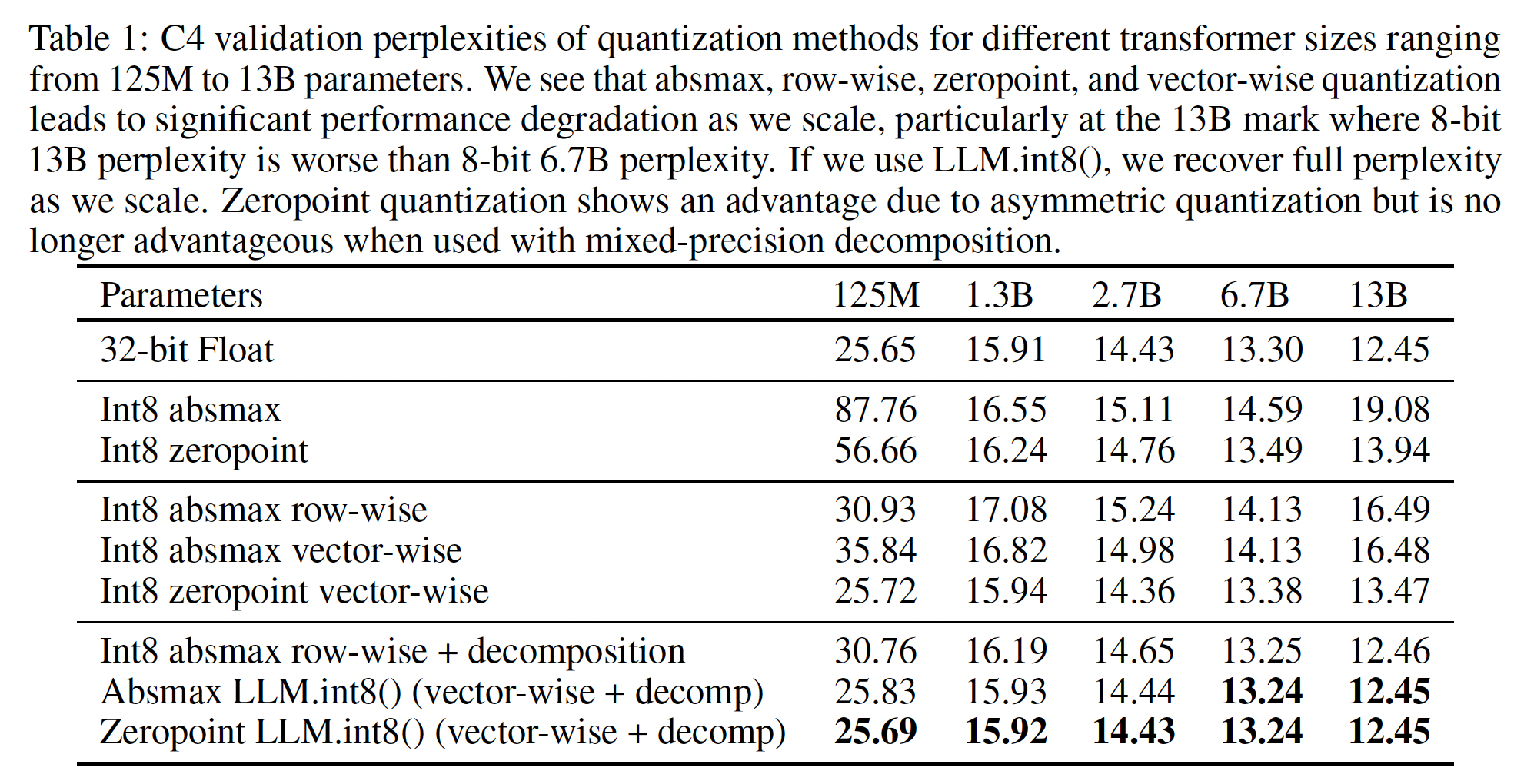
当我们在
Figure 1中查看OPT模型在EleutherAI语言模型评估工具箱上的zero-shot性能的缩放趋势时,我们看到:LLM.int8()随着规模从125M到175B参数的增加保持了full 16-bit性能。另一方面,基线
8-bit absmax vector-wise quantization随着规模的增加表现糟糕,衰退为随机性能。

虽然我们的主要关注点是节省内存,但我们也测量了
LLM.int8()的运行时间。与
FP16基准相比,quantization开销可以拖慢小于6.7B参数模型的推理速度。但是,6.7B参数或更小的模型在大多数GPU上可以正常适配,实际中不太需要量化。对于等效于
175B模型的大矩阵乘法,LLM.int8()的运行时间约快两倍。
附录
D提供了这些实验的更多详细信息。
3.3 大型 transformer 中的离群的大幅值特征
随着
transformer规模的增加,大幅值的异常值特征涌现(emerge)并强烈影响所有层及其量化。给定隐状态sequence/token dimension、hidden/feature dimension。我们将特征定义为特定的hidden/feature dimensiontransformer中所有层的特定feature dimensions我们发现:异常值特征对注意力和
transformer的整体预测性能有很强的影响。13B模型中,每个2048 token sequence中存在多达150k个异常值,但这些异常值特征非常系统化,仅覆盖不超过7个unique feature dimensionszeropoint quantization的优势、以及为何在使用混合精度分解后这些优势消失,以及小型模型vs.大型模型的量化性能。
3.3.1 寻找异常值特征
定量分析涌现现象(
emergent phenomena)的困难有两个方面。我们旨在选择少量特征进行分析,使结果可理解且不太复杂,同时捕获重要的概率模式和结构模式。我们使用一种经验方法来找到这些约束。我们根据以下标准定义异常值:特征的幅值至少为6.0、异常值影响至少25%的层、异常值影响至少6%的sequence dimensions(即,6%的行)。更正式地,给定具有
transformer和隐状态sequence dimensions、feature dimensions,我们将特征定义为隐状态中的特定维度6的维度25%的层中出现,以及至少在6%的行中出现。由于特征异常值仅发生在注意力投影(key/query/value/outpu)和前馈网络扩张层(first sub-layer)中,因此我们忽略注意力函数和FFN收缩层(second sub-layer)进行此分析。我们选择这些阈值的原因如下:
我们发现,使用混合精度分解,如果我们将任何绝对值大于或等于
6的特征作为异常值特征对待,perplexity degradation就会停止。对于异常值影响的层数,我们发现大型模型中的异常值特征是系统性的:要么发生在大多数层、要么根本不出现。
另一方面,在小型模型中,异常值特征是概率性的:对于每个序列,它们有时出现在某些层中。
因此,我们设置检测异常值特征的阈值,使得仅在我们最小的
125M参数模型中检测到单个异常值。这个阈值对应于至少25%的transformer层数受同一feature dimensions的一个异常值的影响。第二常见的异常值仅出现在单个层中(2%的层),这表明这是一个合理的阈值。第二常见的异常值是什么意思?读者猜测是第二大的异常值。
我们使用相同的过程找到异常值特征影响我们
125M模型中多少行:异常值至少影响6%的行(即,sequence dimensions)。
我们测试了高达
13B参数的模型。为了确保观察到的现象不是软件错误造成的,我们评估了在三个不同软件框架中训练的transformer。我们评估了使用OpenAI软件的四个GPT-2模型、使用Fairseq软件的五个Meta AI模型、以及使用Tensorflow-Mesh的一个EleutherAI模型GPT-J。更多细节请参见附录C。我们还在两个不同的推理软件框架Fairseq和Hugging Face Transformers中执行我们的分析。从下表可以看到:
C4 validation perplexity越低,出现的异常值越多。异常值通常是单侧的,它们的四分位数范围显示,异常值的幅值比其他
feature dimensions的最大幅值大3 ~ 20倍,而其他feature dimensions的范围通常为[-3.5, 3.5]。随着规模的增加,异常值在
transformer的所有层中变得越来越常见,并且它们几乎出现在所有的sequence dimensions中。在
6.7B参数时发生了一个相变(phase shift),对于约75%的所有sequence dimensions(SDim),同一异常值出现在同一feature dimensions的所有层中。尽管只占所有特征的约0.1%,但这些异常值对大的softmax概率至关重要。如果删除异常值,平均
top-1 softmax概率会缩小约20%。因为异常值在sequence dimensionsabsmax量化,并有利于非对称的zeropoint量化。这解释了我们验证困惑度分析中的结果。
这些观察结果似乎是普遍的,因为它们出现在不同软件框架中训练的模型中(
fairseq、OpenAI、Tensorflow-mesh),并且它们出现在不同的推理框架中(fairseq、Hugging Face Transformers)。这些异常值似乎也对transformer架构的细微变化稳健(rotary embeddings、embedding norm、residual scaling、不同初始化)。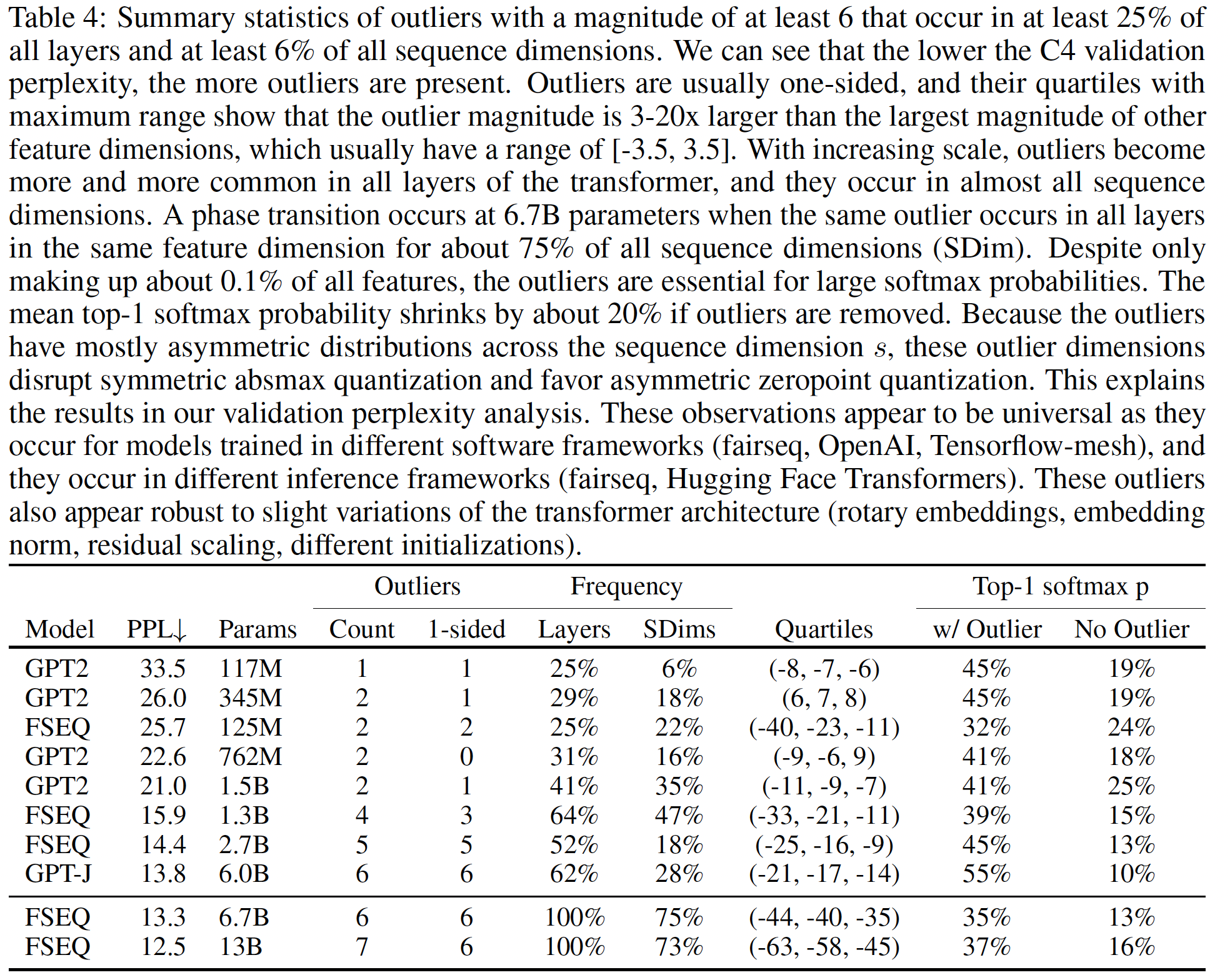
3.3.2 测量异常值特征的影响
为了证明异常值特征对注意力和预测性能至关重要,我们在将隐状态
top-1 softmax概率与常规的包含异常值的softmax概率进行比较。我们对所有层独立地执行此操作,这意味着我们forward常规的softmax概率值从而避免cascading errors并隔离由异常值特征引起的效应。如果我们删除outlier feature dimension(即,将其设为零)并通过transformer传播这些被改变的隐状态,我们还报告perplexity degradation。作为对照,我们对随机的non-outlier feature dimensions应用相同的程序,并注意attention and perplexity degradation。我们的主要定量结果可以总结为四个要点:
(1):当以参数数量衡量时,大幅值特征在transformer所有层之间的涌现,在Figure 3a所示,在6B至6.7B参数之间突然发生,受影响的层百分比从65%增至100%。受影响的sequence dimensions数量迅速从35%增加到75%。这种突然的shift与量化开始失败的时机同时发生。(2):另一方面,当以困惑度衡量时,大幅值特征在transformer所有层之间的涌现,可以看做是根据decreasing perplexity的指数函数平滑出现,如Figure 3b所示。这表明涌现没有什么突然,通过在更小的模型中研究指数趋势,我们可能能在发生相变之前检测到离群特征(emergent features)。这也表明涌现不仅与模型大小有关,还与许多其他因素有关,例如所使用的训练数据量和数据质量(《Training compute-optimal large language models》、《Scaling laws for autoregressive generative modeling》)。(3):一旦异常值特征出现在transformer的所有层中,median outlier feature magnitude就迅速增加,如Figure 4a所示。异常值特征的大幅值和不对称分布扰乱了Int8量化精度。这是6.7B规模开始量化方法失败的核心原因:量化分布(quantization distribution)的范围太大,以至于大多数quantization bins是空的,small quantization values被量化为零,本质上销毁了信息。我们假设,除了Int8推理之外,常规的16-bit浮点训练在超过6.7B规模后也会不稳定(如果向量相乘,而向量被填充了magnitude为60的值,很容易偶然超过最大的16-bit值65535)。(4):如Figure 4b所示,随着C4 perplexity的降低,异常值特征的数量严格单调增加,而与模型大小的关系是非单调的。这表明模型困惑度而不是模型大小确定了相变。我们假设模型大小只是达到涌现所需的许多协变量中的一个重要协变量。
相变发生后,这些异常值特征高度系统化。例如,对于一个序列长度为
2048的6.7B参数transformer,我们发现对于整个transformer,每个sequence约有150k个异常值特征,但这些特征仅集中在6个不同的hidden dimensions中。这些异常值对
transformer性能至关重要。如果删除异常值,平均top-1 softmax概率从约40%降低到约20%,验证困惑度增加600-1000%,即使最多只有7个outlier feature dimensions。而当我们删除7个随机的feature dimensions时,top-1 softmax概率仅降低0.02-0.3%,困惑度增加0.1%。这突显了这些feature dimensions的关键性质。这些异常值特征的量化精度至关重要,因为即使轻微的错误也会对模型性能产生巨大影响。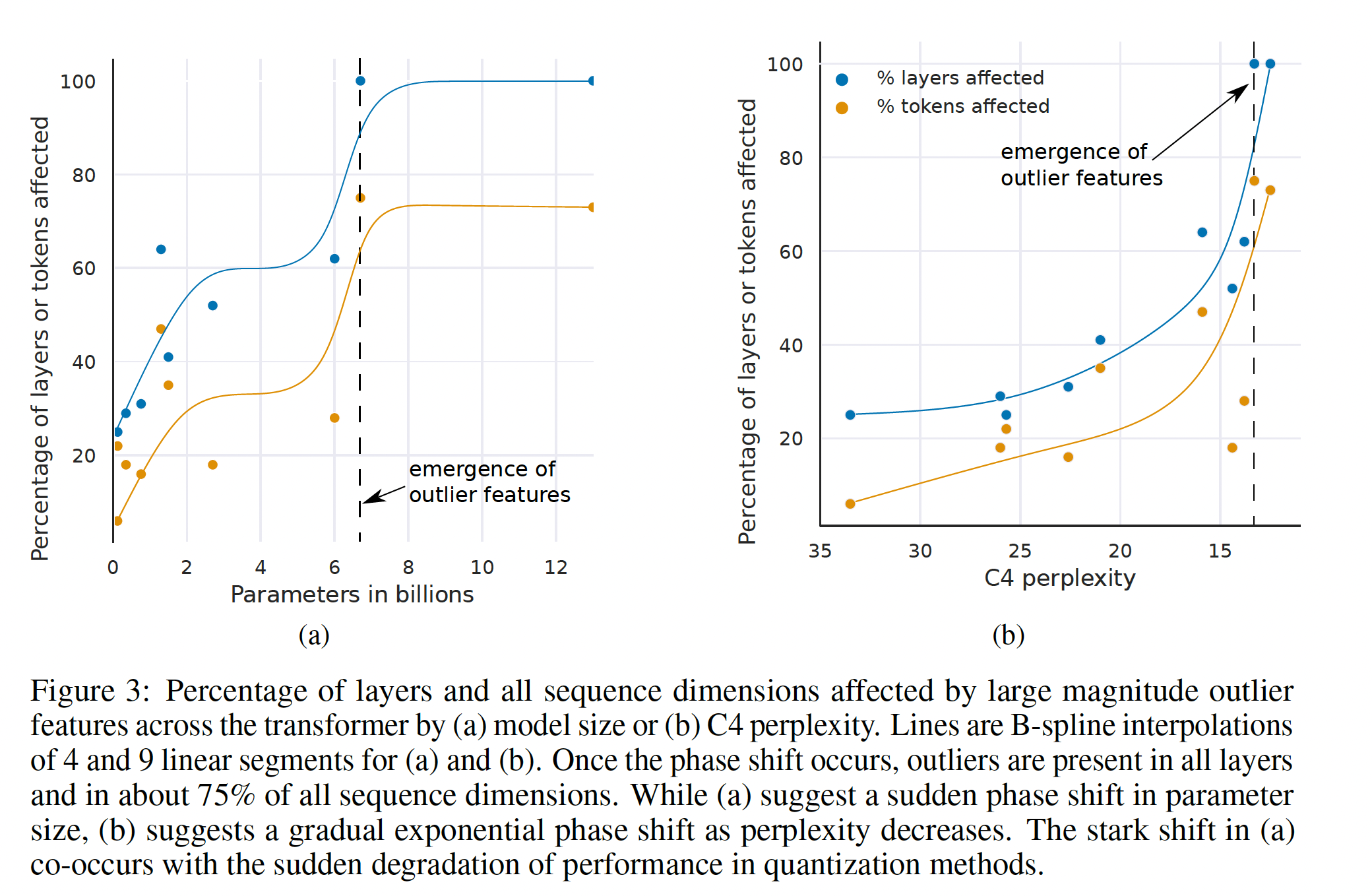

3.3.3 量化性能的解释
我们的分析表明,特定
feature dimensions的异常值在大型transformer中无处不在,这些feature dimensions对transformer性能至关重要。由于row-wise and vector-wise quantization对每个hidden state sequence dimensionfeature dimensionabsmax量化方法在emergence后迅速失败的原因。但是,几乎所有异常值都有严格的非对称分布:它们要么仅为正,要么仅为负(参见附录
C)。这使得zeropoint量化对这些异常值特别有效,因为zeropoint量化是一种非对称量化方法,可以将这些异常值缩放到完整范围[-127, 127]中。这解释了我们的quantization scaling benchmark(Table 1)中zeropoint量化的强大性能。但是,在13B参数规模,即使是zeropoint量化也会由于累积的量化误差和outlier magnitudes的快速增长而失败,如图Figure 4a所示。如果我们使用完整的
LLM.int8()方法及混合精度分解,zeropoint量化的优势消失,这表明remaining decomposed features是对称的。但是,与row-wise quantization相比,vector-wise仍具有优势,这表明增强模型权重的量化精度对保持完整的预测性能至关重要。
3.4 讨论和局限性
我们首次证明,十亿参数级的
transformer可以量化为Int8并立即用于推理,而不降低性能。我们通过使用我们在大规模分析出现的大幅值特征获得的见解来开发混合精度分解,从而将异常值特征隔离在单独的16-bit矩阵乘法中。结合我们的vector-wise quantization方法,我们经验证明可以恢复高达175B参数模型的完整推理性能。局限性:
我们工作的主要局限性是:我们的分析仅针对
Int8数据类型,未研究8-bit浮点(FP8)数据类型。由于当前GPU和TPU不支持此数据类型,我们认为这最好留待未来工作。但是,我们也认为Int8数据类型的许多见解将直接转换为FP8数据类型。另一个局限性是:我们只研究了高达
175B参数的模型。虽然我们将175B模型量化为Int8而不降低性能,但在更大规模上,额外的emergent properties可能会破坏我们的量化方法。第三个局限性是:我们没有对注意力函数使用
Int8乘法。由于我们的重点是减少内存占用,而注意力函数不使用任何参数,所以这并不是绝对必要的。然而,对这个问题的初步探索表明,需要除了这里开发的之外的其他量化方法,我们留待未来工作。最后一个局限性是:我们关注推理但不研究训练或微调。我们在附录
E中对大规模Int8微调和训练进行了初步分析。大规模Int8训练需要在量化精度、训练速度、以及工程复杂性之间进行复杂的trade-off,这是一个非常困难的问题。我们同样留待未来工作。
更广泛的影响:我们工作的主要影响是,使以前因
GPU内存有限而无法适配的大型模型变得可访问。这使得以前由于GPU内存有限而无法进行的研究和应用成为可能,特别是对资源最少的研究人员。Table 2列出了现在可以在不降低性能的情况下访问的model/GPU组合。但是,我们的工作也使得拥有许多GPU的资源丰富的组织可以在相同数量的GPU上serve更多模型,这可能会增加资源丰富和资源贫穷组织之间的差距。具体而言,我们认为公开发布大型
pretrained模型(例如最近的Open Pretrained Transformers: OPT)以及我们对zero-shot and few-shot prompting的新的Int8推理,将为以前由于资源约束而无法进行的学术机构启用新的研究。这种大型模型的广泛可访问性可能对社会产生难以预测的有益的和有害的影响。
四、ZeroQuant [2022]
论文:
《ZeroQuant: Efficient and Affordable Post-Training Quantization for Large-Scale Transformers》
大型自然语言模型已经在不同的应用中被广泛采用,例如使用
BERT进行自然语言理解,以及使用GPT-style模型进行生成任务。虽然这些模型已经取得了SOTA的准确性,但随着模型规模的剧增,部署它们所需的内存占用和计算成本已经成为一个主要的瓶颈,即使是在强大的GPU云服务器上也是如此。量化是缓解这一挑战的一个有前景的方法,它可以降低权重和
activations的bit precision,以达到更小的内存占用、以及更快的计算(例如T4/A100上的INT8 Tensor cores)。然而,量化通常需要重新训练(也称为quantization aware training: QAT)来恢复由weight and activations的representation loss导致的准确率下降。为启用QAT,通常需要完整的训练流程(包括训练数据和计算资源),从而微调模型。现在访问这些组件的机会往往是没有的,而QAT也是一个非常耗时的过程,特别是对于那些大型模型。最近,
zero-shot quantization(《Zeroq: A novel zero shot quantization framework》、《Data-free quantization through weight equalization and bias correction》)和post-training quantization: PTQ(《Up or down? adaptive rounding for post-training quantization》、《Post-training quantization for vision transformer》)被提出,从而解决训练数据访问和计算需求的挑战,因为PTQ通常不需要(或只需要很少的)重新训练。但是大多数这些工作主要关注相对较小规模的计算机视觉问题。更近期,《Understanding and overcoming the challenges of efficient transformer quantization》在BERT上展示了有前景的PTQ结果。然而:(1):它的主要关注点是BERT_base上的高精度量化(INT8/FP16)。(2):它没有考虑其他规模达十亿级别的参数的生成式模型(GPT-3-style模型)。
更重要的是,大多数这些工作没有报告真实的延迟改进,这就质疑了这些方法在改进
inference latency方面的有用性。例如,现有的工作通常不讨论与不同量化方案相关的quantization/dequantization成本,而这实际上对使用低精度带来的性能收益有很大影响。此外,对于极端量化(例如
INT4),通常使用知识蒸馏来提高性能,与QAT相比这又增加了昂贵的计算成本。而且,为了取得更好的准确率性能,通常对quantized model应用hidden-states knowledge distillation,例如《Binarybert: Pushing the limit of bert quantization》、《Ternarybert: Distillation-aware ultra-low bit bert》。这会给GPU内存和计算资源需求带来巨大压力,因为teacher模型和student模型都需要加载到GPU内存中进行训练。在本文中,我们提出
ZeroQuant,一个端到端的post-training quantization and inference pipeline,以解决这些挑战,目标是INT8和INT4/INT8混合精度量化。具体来说,我们的贡献如下:我们对权重和
activations应用细粒度的硬件友好的量化方案,即权重的group-wise quantization(即,列维度)、以及activations的token-wise quantization(即,行维度)。这两种量化方案都可以显著减少量化误差并保留hardware acceleration特性。我们提出了一种新的
layer-by-layer knowledge distillation: LKD用于INT4/INT8混合精度量化,其中神经网络通过最小迭代的知识蒸馏被layer-by-layer地量化,甚至不需要访问原始训练数据。因此,在任意时刻,设备内存主要仅加载单个额外layer的占用,这使得规模达十亿级参数的模型蒸馏在有限的训练预算和GPU设备下成为可能。我们开发了一个高度优化的推理后端(
inference backend),消除了quantization/dequantization算子的高昂计算成本,在现代GPU硬件的INT8 Tensor cores上实现了延迟加速。我们的经验结果显示:
ZeroQuant可以将BERT和GPT-3-style模型量化为INT8权重和activations从而保留准确性,而不会产生任何重新训练成本。与FP16推理相比,在A100 GPU上,我们的INT8模型在BERT_base/GPT-3_350M上获得了高达5.19x/4.16x的加速。ZeroQuant puls LKD可以进行BERT和GPT-3-style模型的INT4/INT8混合精度量化。与FP16模型相比,这导致了3倍的内存减少,准确率损失可以忽略。而且,得益于LKD的轻量级,我们可以在33秒(BERT_base)和10分钟(BERT_large)内完成量化过程。我们还展示LKD可以使用其他数据集达到类似于原始训练数据的性能。我们展示了
ZeroQuant在两个最大的开源语言模型GPT-J_6B和GPT-NeoX_20B上的可扩展性,使用INT8量化。ZeroQuant可以在GPT-J_6B上实现比FP16模型快3.67倍;并且ZeroQuant将GPT-NeoX_20B的GPU需求从2减少到1,延迟从65ms降低到25ms(整体系统效率提高5.2倍)。
本文的主要贡献是两个:
layer-by-layer knowledge distillation、以及高度优化的推理后端。相关工作:人们从不同方面探索了模型压缩。其中,量化是最有前景的方向之一,因为它可以直接减少内存占用和计算强度。这里我们聚焦
NLP模型的量化,并简要讨论相关工作。大多数量化工作可以归类为
quantization-aware training: QAT。《Q-BERT: Hessian based ultra low precision quantization of bert》和《Q8BERT: Quantized 8bit bert》是第一批使用整数对权重和activations进行BERT模型量化的工作。具体而言,《Q-BERT: Hessian based ultra low precision quantization of bert》利用Hessian信息将权重bit-precision推到INT2/INT4,它还提出了group-wise quantization,从而比single matrix quantization更细粒度的方式对权重矩阵进行量化。《Training with quantization noise for extreme fixed-point compression》引入quantization noise以缓解QAT的方差。《Ternarybert: Distillation-aware ultra-low bit bert》、《Binarybert: Pushing the limit of bert quantization》利用非常昂贵的知识蒸馏 (《Distilling the knowledge in a neural network》)和数据增强 (《Tinybert: Distilling bert for natural language understanding》)从而ternarize/binarize权重。《Kdlsq-bert: A quantized bert combining knowledge distillation with learned step size quantization》结合知识蒸馏和learned step size quantization(《Learned step size quantization》)将权重量化到2-8 bits。最近,
《Compression of generative pre-trained language models via quantization》也使用知识蒸馏将GPT-2模型在特定任务上压缩到INT2。
所有这些工作都是使用原始训练数据集对模型进行量化的。更重要的是,它们需要重新训练、或微调整个模型来恢复准确率。这种
extra-large models(比如megatron-turing nlg 530b, Palm)的计算成本,对大多数研究实验室或从业者来说几乎是不可承受的。克服计算成本挑战的一种解决方案是
post-training quantization: PTQ。然而,PTQ通常会导致显著的准确率下降,因为网络对量化误差敏感。沿着这条线,
Transformer-based模型的第一批工作之一是《Gobo: Quantizing attention-based nlp models for low latency and energy efficient inference》。作者提出了基于质心的量化方法,其中outlier numbers使用FP32格式,其余numbers使用non-uniform quantization。因此,很难在general compute accelerators(如CPU和GPU)上获得真实的inference latency收益,因为这些硬件中的parallel processing units不支持混合数据类型的有效计算。更近期地,
《Understanding and overcoming the challenges of efficient transformer quantization》为模型的一部分引入了高精度的activation quantization(FP16)以克服high dynamic activation ranges。
但是,据我们所知:
(1): 在先前的工作中还没有研究如何在GPT-3-style模型上应用PTQ而达到高准确率。(2):如何在十亿级规模的模型上应用PTQ仍较少被探索。(3):高效的推理系统后端(inference system backend)仍然缺失,尤其是对于细粒度量化方案,这使得很难在通用硬件上获得低延迟。
ZeroQuant通过考虑system backend融入算法设计来解决所有这些局限性。我们在BERT和大型GPT-3-style模型(高达20B参数,即GPT-NeoX_20B)上验证了ZeroQuant的能力,用于各种任务。
4.1 背景和挑战
我们在附录
A中简要概述了Transformer架构和量化背景。请参阅《Attention is all you need》和《A survey of quantization methods for efficient neural network inference》以了解更多关于Transformer架构和量化的细节。与
QAT相比,PTQ展现了更大的压缩效率,因为PTQ通常被用于quantize the model而无需重新训练。PTQ的一种常见策略是将训练数据馈入网络,并使用running mean来校准scaling factorB.1。一些工作已经在
BERT_base模型上完成,使用INT8权重和混合INT8/FP16的activation量化。然而,还没有针对:(1):BERT模型上的更bit-precision的PTQ进行研究。(2): 大型GPT-3-style模型进行研究。
这里,我们简要讨论在
BERT(见附录C)和GPT-3-style模型上应用PTQ的挑战。Table 1显示了带PTQ的GPT-3_350M的结果。可以看出:INT8 activation quantization(即W16A8的行)引起了主要的accuracy loss。进一步将权重推到
INT8(即W8A8的行)不改变zero-shot评估任务的准确率,但导致因果语言建模任务(Wikitext-2)的困惑度得分变差;这表明与其他zero-shot问题相比,生成式任务的敏感性。对于
W4/8A16,在一些accuracy-based的任务上,GPT-3350M仍然达到了合理的性能,如OpenBookQA;但它在大多数其余任务上损失了准确率。特别是对于Wikitext-2,具有W4/8A16的GPT-3_350M无法再生成任何有意义的文本。
BERT的分析请参见附录C。WaAb表示:对权重采用a-bit、对activation采用b-bit。W4/8A16表示:对权重混合采用4-bit和8-bit、对activation采用16-bit。其中,将自注意力计算的权重量化为INT8、feed-forward connection: FFC的权重量化为INT4。W8A8/16表示:对权重采用8-bit、对activation混合采用8-bit和16-bit。其中,将自注意力计算的input activation使用FP16 activation,对其余计算使用INT8。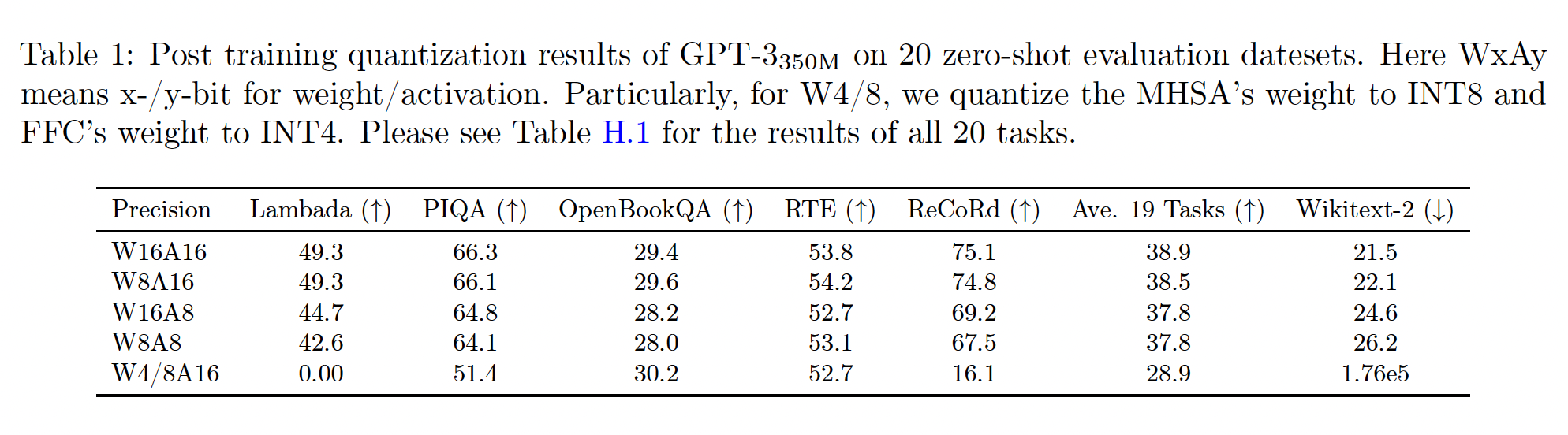
Dynamic Activation Range:为了研究为什么INT8 activation对BERT和GPT-3-style模型都导致显著的准确率下降,我们在Figure 1(left)中绘制了GPT-3_350M不同Transformer layers的每个activation的token-wise(即,行维度)的range。可以看出,不同token具有极大的activation ranges差异。例如,最后一层的maximum range约为35、而minimum range接近8。这种activation range的较大方差使得使用固定的quantization range(通常是最大值)对所有token进行量化以保持预测准确率变得困难,因为对于small range tokens的limited representation能力会损害准确率性能。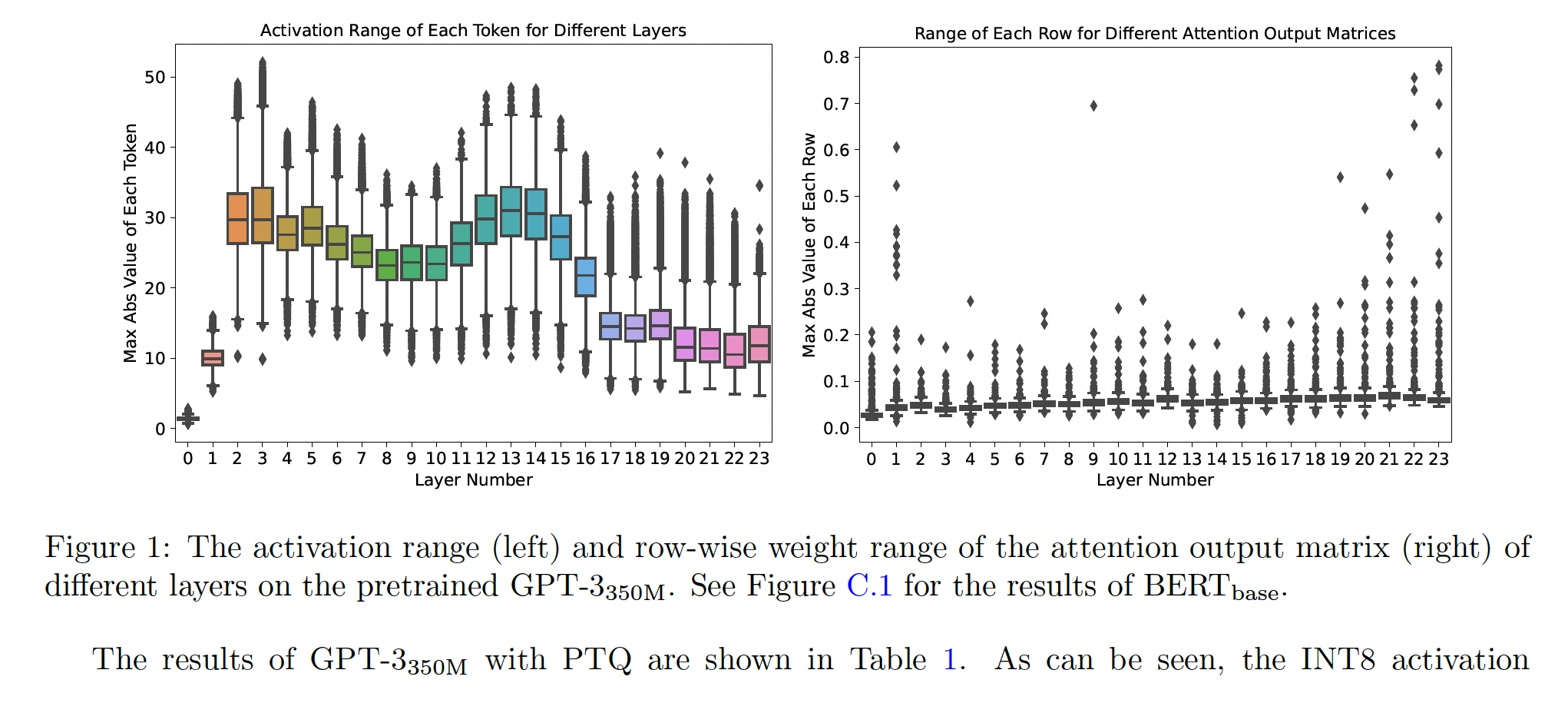
Different Ranges of Neurons in Weight Matrices:类似地,我们在Figure 1(right)中绘制了GPT-3_350M的attention output matrix(即,output dimension))的weight range。不同行之间的largest magnitudes存在10倍的差异,这导致INT8 weight PTQ的generation性能变差。当应用INT4量化时,这也提出了很大的挑战,因为INT4只有16个数字,更小10倍的范围导致这些smaller-range rows的representations只有2或3个数字。这些分析结果也表明了为什么需要更昂贵的
hidden-states knowledge distillation来进行ultra-low precision quantization以弥合准确率差距。但是,由于大型模型的训练成本太高,因此需要一个轻量级的和高效的方法进行PTQ。
4.2 方法
4.2.1 细粒度的硬件友好的量化方案
如前所述,即使对
BERT/GPT-3-style模型应用INT8 PTQ也会导致显著的准确率下降。关键挑战是INT8的representation并不能完全捕获权重矩阵中不同行的、以及不同activation tokens的数值范围。一种解决方法是对权重矩阵(或activations)采用group-wise (token-wise) quantization。Group-wise Quantization for Weights:group-wise weight matrix quantization首先在《Q-BERT: Hessian based ultra low precision quantization of bert》中被提出,其中权重矩阵《Q-BERT: Hessian based ultra low precision quantization of bert》中,作者仅将此应用于quantization aware training。更重要的是,他们没有考虑硬件效率约束(hardware efficiency constraint),也没有系统后端支持。因此,他们缺乏真实的latency reduction效益。在我们的设计中,我们考虑了
Ampere Architecture的GPU(例如A100)的硬件约束,其中计算单元基于Warp Matrix Multiply and Accumulate (WMMA) tiling size(《Using tensor cores in cuda fortran》)从而实现最佳加速。接下来,我们将展示,与single-matrix quantization相比,我们的group-wise quantization由于更细粒度的量化而具有更好的准确率,同时仍然实现了很大的latency reduction。group-wise weight matrix quantization是怎么实现的?读者猜测是对权重矩阵按照block来进行量化。Token-wise Quantization for Activations:如前面内容和附录A.2所述,现有PTQ工作的一种常见做法是:对activation使用静态量化,其中min/max range在离线校准阶段(offline calibration phase)计算。这种方法对于activation range方差较小的小型模型可能就足够了。然而,正如前面分析的那样,对于GPT-3_350M和BERT_base等大型Transformer模型,activation range存在巨大的方差。因此,静态量化方案(通常应用于所有tokens/samples)会导致显著的准确率下降。克服这个问题的一个自然想法是:采用更细粒度的token-wise quantization,并为每个token动态地计算min/max range以减少来自activations的量化误差。我们在实验部分的评估也显示了token-wise quantization对GPT-3-style和BERT模型的准确率有显著改善。token-wise quantization是怎么实现的?读者猜测:是对activation矩阵按行进行量化。然而,直接在现有的深度学习框架(如
PyTorch quantization suite)中应用token-wise quantization会导致显著的quantization and dequantization成本,因为token-wise quantization引入了额外的操作,这些操作导致GPU计算单元和主内存(main memory)之间的昂贵的数据移动开销。为解决此问题,我们为transformer模型的token-wise quantization构建了一个高度优化的推理后端(inference backend)。例如,ZeroQuant的推理后端采用所谓的kernel fusion技术,将quantization operator与其前面的算子(如layer normalization)融合,以减轻token-wise quantization带来的数据移动成本。类似地,不同GeMM's output的逆量化成本,通过如下方式缓解:在将final FP16 result写回主内存以供下一个FP16算子(如GeLU)使用之前,使用weight and activation quantization scales对INT32 accumulation进行缩放。这些优化将在接下来详细讨论。token-wise quantization可以显著减少quantized activations的representation error。而且,由于它不需要校准activation range,接下来我们将展示对于中等量化方案(INT8 weight with INT8 activation),ZeroQuant不会产生任何与量化相关的成本(例如activation range calibration)。注意,论文实验部分提到,对于大型模型(如
GPT-NeoX_20B),需要将自注意力的input activation保持为FP16。如果将自注意力的input activation量化为INT8甚至INT4,则会带来accuracy loss。
4.2.2 Layer-by-layer Knowledge Distillation with Affordable Cost
知识蒸馏(
knowledge distillation: KD)是减轻模型压缩后准确率下降的最强大方法之一。然而,KD存在几个局限性,特别是在大型语言模型上的hidden-states KD:(1):KD需要在训练期间同时持有teacher模型和student模型,这大大增加了内存和计算成本。(2):KD通常需要full training学生模型。因此,需要在内存中存储权重参数的若干副本(梯度、一阶动量、二阶动量等)以更新模型。(3):KD通常需要原始训练数据,而由于隐私/保密问题,有时无法访问这些数据。
为解决这些局限性,我们提出了
layer-by-layer distillation: LKD算法。假设要量化的目标模型有transformer blocks,LKD逐层地对网络进行量化,并使用其原始版本(即unquantized版本)作为teacher模型。具体而言,假设层
quantized版本是first k-1 layers上对其中:
MSE是均方误差,也可以替换为其他损失函数(例如KL散度)。可以看出:
(1):我们的LKD不需要单独的teacher模型,因为我们对teacher/student模型都使用相同的每次仅仅调整
quantized版本的一层,因此是一种贪心算法。(2):optimizer states的内存开销显著减少,因为唯一优化的层是(3):由于我们从不优化end-to-end model,训练不再依赖标签。后面我们将在实验章节中展示LKD不依赖于原始训练数据。论文的实验部分展示:即使采用随机生成的
token ids,LKD也能够提升模型的性能。从实验部分可以看到:
LKD对于生成式任务的提升,相比分类任务,要更大。
4.2.3 Quantization-Optimized Transformer Kernels
优化
inference latency和模型大小对于实际部署大型Transformer模型至关重要。在推理期间,batch size通常相对较小,所以模型的inference latency主要取决于从主内存加载所需推理数据的时间。通过将weights and activations量化为较低精度,我们减少了加载这些数据所需的数据量,这允许更有效地利用内存带宽、以及更高的加载吞吐量。但是,简单地将weights/activations转换为INT8并不能保证改善延迟,因为存在一些与quantization/dequantization操作相关的额外的数据移动开销,如Figure 2所示的红色框。这样的开销变得昂贵,在某些情况下超过了使用低精度的性能收益。为了获得
token-wise quantization带来的准确率提升和延迟改善,我们现在介绍我们的优化:通过最大化内存带宽利用率(memory bandwidth utilization)来加速ZeroQuant的inference latency。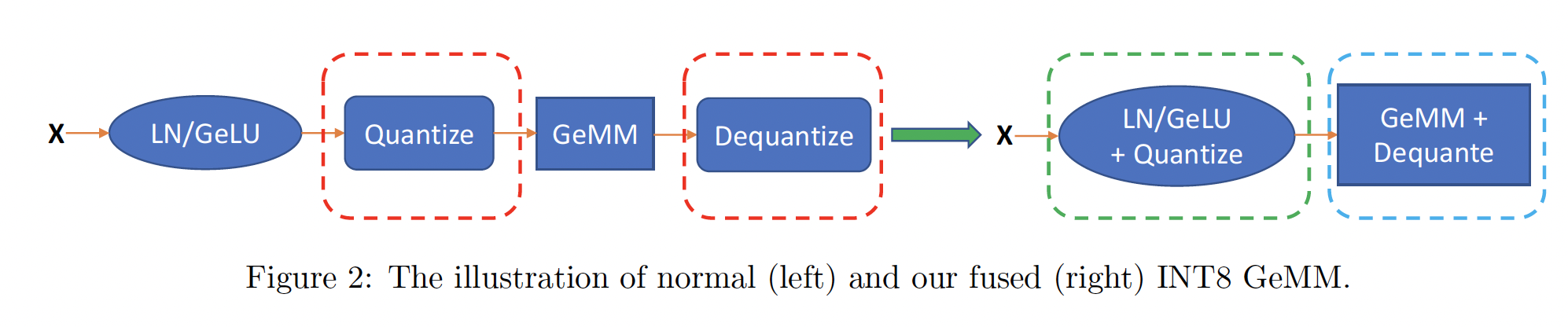
CUTLASS INT8 GeMM:为支持INT8计算, 我们使用针对不同batch sizes进行了调优的CUTLASS INT8 GeMM实现。与标准GPU后端库(如cuDNN)不同,使用CUTLASS允许我们更灵活地在GeMM之前和之后融合量化操作,以减少kernel launching和数据移动的开销。Fusing Token-wise Activation Quantization:token-wise quantization/dequantization引入了许多额外的操作,导致额外的数据移动成本。为消除这些成本,我们使用kernel fusion,将activation的量化操作与其前面的element-wise and/or reduction操作(如bias-add, GeLU, and LayerNorm)融合为单个算子,如Figure 2中的绿色框所示。对于逆量化操作(例如逆量化来自GeMM算子的integer output),我们类似地将其与我们的自定义GeMM schedule融合,从而避免额外的read/write访问主内存,如Figure 2中的蓝色框所示。通过上述优化,我们能够在实验章节中展示
BERT和GPT-3-style模型的显著的延迟减少。有关我们的系统优化的更多细节,请参见附录D。
4.3 实验
为评估提出的
ZeroQuant,我们在BERT和GPT-3模型上测试它。对于
BERT,我们在GLUE benchmark中测试了BERT_base和BERT_large。对于
GPT-3-style模型,我们在20个zero-shot评估任务上测试了GPT-3_350M(即具有350M参数的GPT-3-style模型)和GPT-3_1.3B(即具有1.3B参数的GPT-3-style模型),包括19个accuracy-based任务和1个language modeling generation任务。
为了展示提出的
ZeroQuant的可扩展性,我们还直接将其应用于两个最大的开源GPT-3-style模型,即GPT-J_6B和GPT-NeoXP20B。对于所有与LKD相关的实验,我们使用固定的超参数集合,尽管调优它们可能有利于我们的结果。请参阅附录B.2以获得更多关于训练的详细信息,并参阅附录B.3以获得报告的BERT指标。为提供全面研究,我们还在附录E中包括BERT的调参结果、以及针对本节中不同的proposed components的消融研究。符号解释:
我们使用
WxAy表示对权重使用x-bit量化、对activation使用y-bit量化。除非特别说明:
对于
W4/8,我们将multi-head self attention: MHSA的权重量化为INT8、feed-forward connection: FFC的权重量化为INT4。对于
A8/16,我们对自注意力计算(即与GeMM)使用FP16 activation,对其余计算使用INT8。
我们使用
ZeroQuant来表示仅具有细粒度量化方案的方法;使用ZeroQuant-LKD来表示同时具有细粒度量化方案和LKD的方法。
4.3.1 BERT 的主要结果
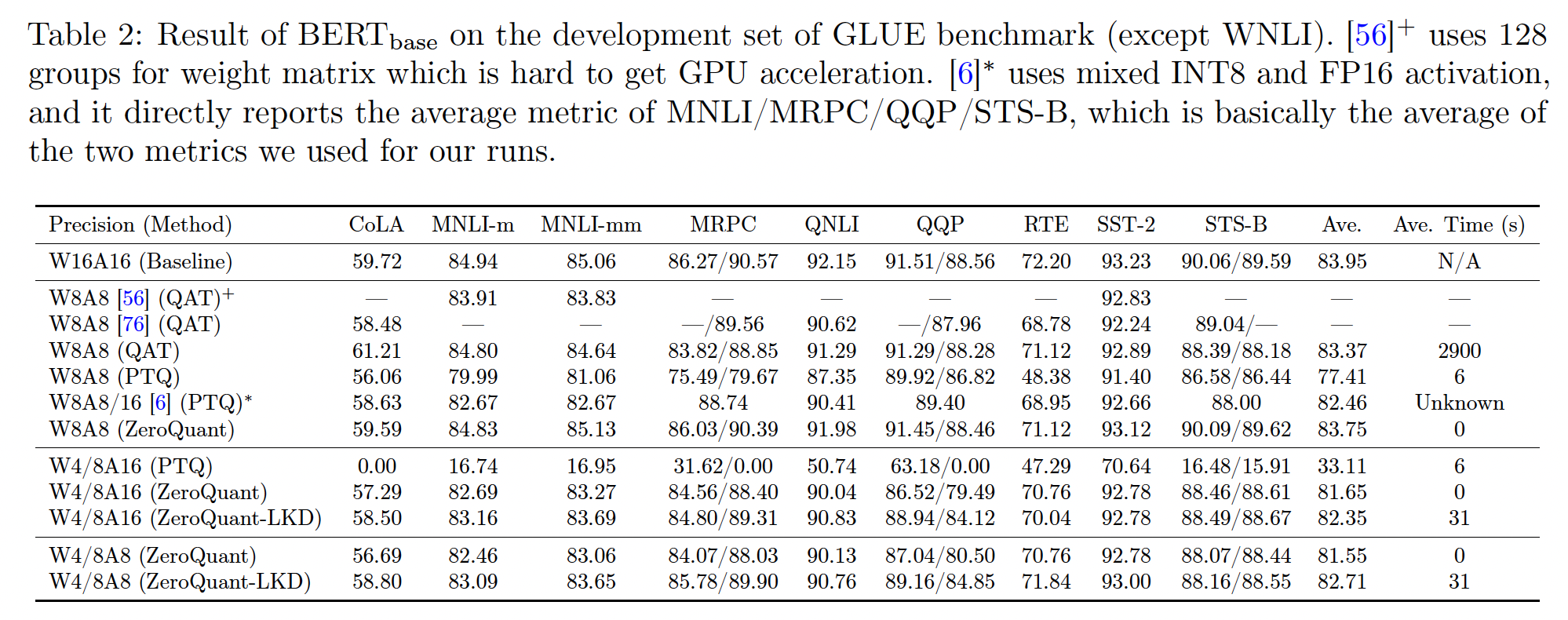
BERT_base:我们在Table 2中报告BERT_base的结果。对于
W8A8,PTQ的平均准确率降低了6分左右。 然而,ZeroQuant可以达到83.75分,仅比基线低0.2。 具体而言,由于ZeroQuant没有activation range calibration阶段,其成本为0,甚至比标准PTQ更便宜。与
《Understanding and overcoming the challenges of efficient transformer quantization》相比(即,[6],1.29)。 与此同时,与ZeroQuant中使用的INT8 activation相比,[6]使用mixed INT8 and FP16 activation。我们还将我们的方法与内部训练的
QAT和其他QAT工作(《Q-BERT: Hessian based ultra low precision quantization of bert》,即[56]《Q8BERT: Quantized 8bit bert》,即[76]QAT方法获得的准确率结果相媲美,针对INT8量化,ZeroQuant可以将重新训练成本从2900s降低到0s(即,无需重新训练)。
对于更激进的、具有
minimal (or no) training quantization的权重量化,即W4/8A16,PTQ完全丢失了所有准确率(纯随机预测)。 然而,ZeroQuant仍然可以达到81.65的平均分数。在ZeroQuant的基础上,如果我们添加LKD,则准确率可以进一步提升到82.35,每个任务的成本仅为31s,仅使用单个GPU,与INT8 QAT量化相比,节省了93.5倍的成本。
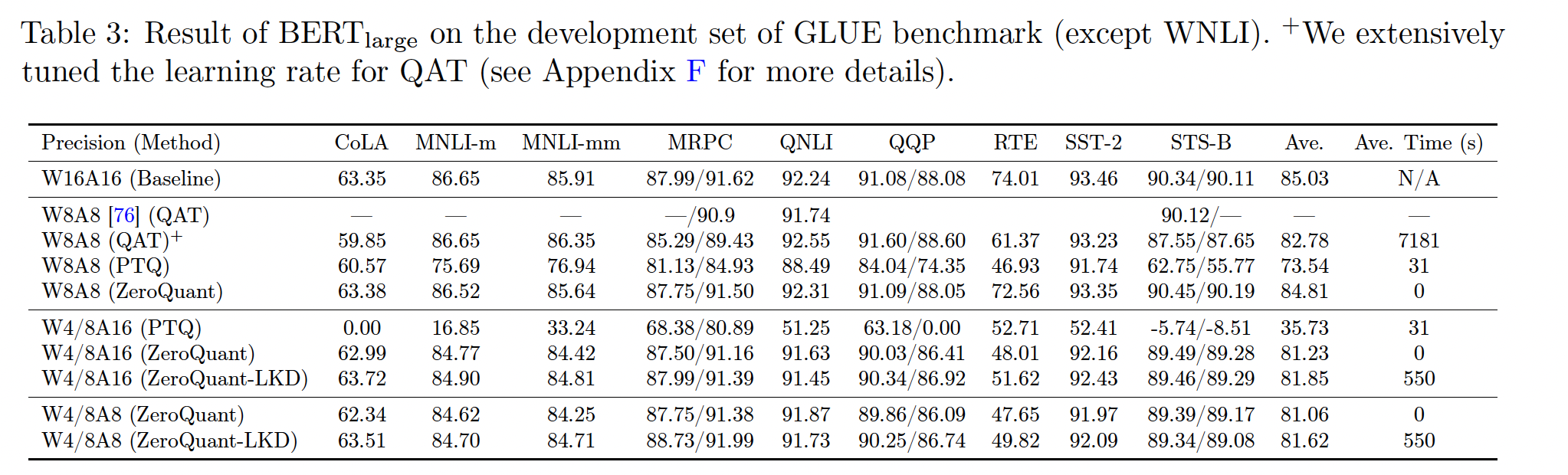
BERT_large:我们也在BERT_large上测试我们的方法,结果如Table 3所示。与
BERT_base类似,ZeroQuant的准确率明显优于PTQ方法。与QAT方法相比,ZeroQuant在更大的数据集(如MNLI/QQP)上具有可比结果,并在小任务(例如CoLA/MRPC/RTE)上具有更好的性能。我们实际上为QAT调优了多个学习率,但即使对于这些小任务也无法获得更好的性能(请参阅附录F以获取更多详细信息)。对于更激进的量化方案,如
W4/8A16和W4/8A8,ZeroQuant和ZeroQuant-LKD仍然达到了很好的准确率,除了RTE之外,模型大小约为FP16模型的3倍。这与INT8 QAT结果一致,后者在RTE上损失了更多的准确率。由于LKD的轻量级成本,即使在BERT_large上也只需要大约550s就可以完成每个任务,比QAT便宜13倍。
4.3.2 GPT-3-style 模型的主要结果
GPT-3_350M:我们首先在GPT-3_350M上测试ZeroQuant和ZeroQuant-LKD,并在Table 4中报告结果。GPT-3-style模型上的zero-shot评估的第一个有趣发现是,与生成式任务相比,accuracy-based任务的accuracy performance更能容忍量化。例如,W8A8 PTQ在19个accuracy-based的任务上平均准确率下降了1.1%,相比之下在Wikitext-2上下降4.7分。在
W8A8上,将ZeroQuant与PTQ进行比较,我们可以将accuracy gap从1.1%降低到0.2%,困惑度(perplexity: PPL)差距从4.7降低到0.2,而无需activation range calibration成本。对于
W4/8A16量化方案,PTQ几乎无法对大多数任务进行合理预测, 其在Wikitext-2上的generation性能完全崩溃。相比之下,ZeroQuant在某些任务上仍然取得了重大的性能,但其在Wikitext-2上的generation性能显著降低。LKD为这种W4/8A16 setting带来了显著的性能提升。请注意,与
ZeroQuant相比,ZeroQuant-LKD将准确率从33.5提高到37.0,困惑度从88.6降低到30.6,而这全部的成本只有3.1小时在单个A100 GPU上。请注意,这约为完整预训练成本(128个A100 GPU,32小时)的0.027%的GPU hours。在
W4/8A8上,与W4/8A16类似,ZeroQuant-LKD通过使用轻量级LKD比ZeroQuant获得了更好的性能。
PTQ为什么需要时间?因为它对activation使用静态量化,其中min/max range在离线校准阶段(offline calibration phase)计算。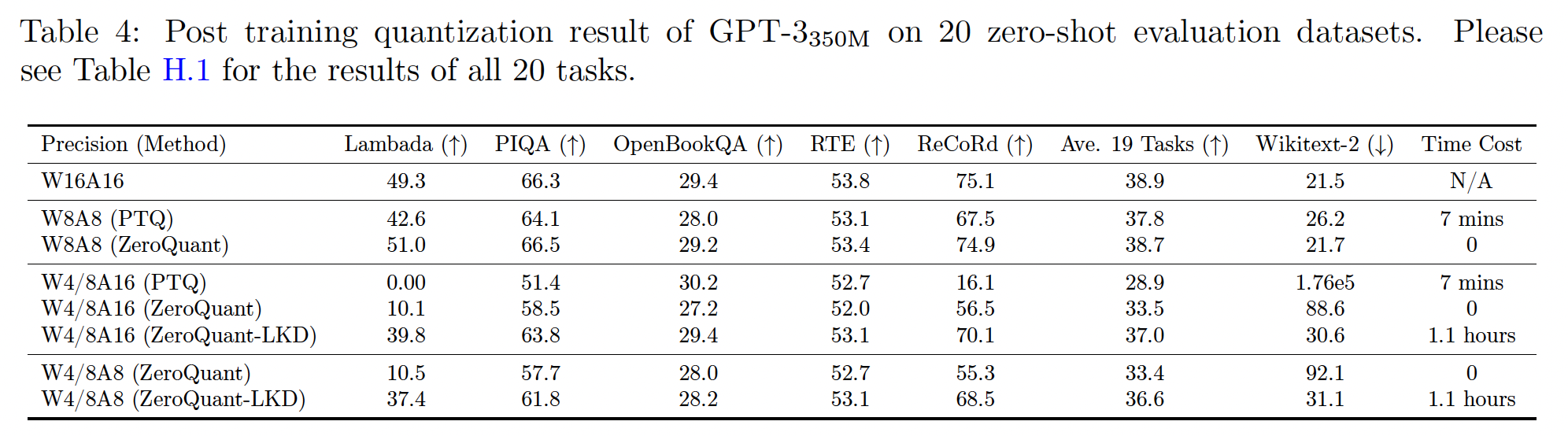
GPT-3_1.3B:GPT-3_1.3B的结果如Table 5所示。与GPT-3_350M类似:对于
W8A8,与PTQ相比,ZeroQuant的性能更好,无activation calibration成本,特别是对于生成式任务Wikitext-2(低3.2分)。此外,对于
W4/8A8量化,LKD可以为ZeroQuant带来重大的性能收益。LKD的成本约为完整预训练成本(128个A100 GPU,120小时)的0.02%。
4.3.3 BERT 和 GPT-3-style 模型的延迟降低
我们在
Table 6中比较了单个40G-A100 GPU上,BERT的FP16版本和我们的INT8版本之间的推理速度。通过使用高效的quantization kernel implementation和算子融合,INT8模型可以在BERT_base上实现2.27-5.19倍的加速,在BERT_large上实现2.47-5.01倍的加速。我们还包括
GPT-3-style模型在FP16和我们的INT8版本之间的延迟比较。具体而言,我们使用模型根据给定文本生成first 50 tokens,并测量平均延迟。与FP16版本相比,我们的INT8模型在GPT-3_350M/GPT-3_1.3B上实现了4.16x/4.06x的加速。
4.3.4 GPT-J_6B 和 GPT-NeoX_20B 的展示
为演示
ZeroQuant的可扩展性,我们将其应用于两个最大的开源模型,即GPT-J_6B和GPT-NeoX_20B,它们分别具有6B和20B参数。我们在
Table 7中报告了GPT-J_6B在三个generation数据集(即PTB、Wikitext-2和Wikitext-103)上的结果。可以看到,
ZeroQuant在所有三个不同任务上都实现了与FP16相差无几的PPL。为了比较延迟,我们再次使用生成前
50 tokens的平均延迟数。与FP16版本相比,我们的W8A8可以获得高达3.67倍的加速。

为
GPT-NeoX_20B的所有GeMM来量化到W8A8会导致准确率显著下降。我们检索每个权重矩阵和每个activation的量化,并最终发现:注意力计算的activation quantization(即,自注意力的输入)导致了accuracy loss。我们推测这是由于超大模型(20B参数)中自注意力模块的敏感性造成的,但由于缺乏开源的超大模型和完整的评估流程,我们无法在其他模型上验证这一点。 因此,我们将自注意力的input activation保持为FP16,其余部分量化为INT8。结果如Table 8所示。我们的W8A8/16实现了与FP16类似的准确率,但可以减少GPU资源需求(从2个A100 GPU减少到1个)和延迟(从65ms降低到25ms),这两者共同导致了5.2倍更好的吞吐量/效率。
4.3.5 不同组件的消融研究
为了研究我们引入的每个组件的性能提升,即
group-wise weight quantization、token-wise activation quantization、以及lightweight layer-by-layer knowledge distillation,我们在此对BERT_large上的W4/8A8进行消融研究。我们在
Table 9中呈现了结果。可以看出:group-wise weight quantization将准确率从PTQ(随机猜测预测)提升到一个重大的结果(66.52)。进一步添加
token-wise quantization可以提高14.54分的准确率。在这些基础上(即
ZeroQuant),LKD进一步带来了0.56分的提升。
4.3.6 无法访问原始训练数据
如前几节所述,由于隐私和/或保密问题,原始训练数据通常很难访问。因此,我们这里研究当没有直接访问原始训练数据时,我们的
LKD的性能。由于LKD的蒸馏目标不依赖标签,LKD使用的训练数据可以非常灵活。我们使用三种不同的训练数据资源,从而比较
GPT-3_350M在W4/8A8量化方案上的性能:即,随机数据(使用随机整数编号生成token ids)、维基百科(使用Huggingface获取数据)、原始PILE数据集。结果如Table 10所示。与
ZeroQuant相比,使用随机数据的LKD可以将准确率提高1.1%,困惑度从92.1降低到40.6。随机数据仍然可以显著提高性能的原因是:LKD不优化end-to-end pipeline,而是仅逐层学习来自teacher模型的内部依赖关系。因此,随机数据也可以提供有意义的信息。使用
Huggingface的Wikipedia数据可以进一步将准确率提高到36.2,困惑度降低到30.4,这与使用原始数据的结果相当。这表明,当我们无法访问完整的原始数据集时,可以使用干净的文本数据集进行LKD。

五、SmoothQuant [2022]
论文:
《SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models》
大型语言模型(
LLM)在各种任务上展示了出色的性能。然而,由于模型规模巨大,部署LLM需要大量的预算和能源。例如,GPT-3模型包含175B参数,至少需要350GB内存来存储和以FP16运行,仅进行推理就需要8 * 48GB A6000 GPU或5 * 80GB A100 GPU。由于巨大的计算和通信开销,inference latency也可能无法被实际应用所接受。量化是减少LLM成本的有希望的方法(《Llm.int8(): 8-bit matrix multiplication for transformers at scale》、《Zeroquant: Efficient and affordable post-training quantization for large-scale transformers》)。通过用low-bit整数来量化权重和activations,我们可以减少GPU内存需求(大小和带宽),并加速计算密集型操作(即,线性层中的GEMM和注意力中的BMM)。例如,与FP16相比,权重和activations的INT8量化可以将GPU内存使用量减半,矩阵乘法的吞吐量提高近一倍。
然而,与
CNN模型或较小的transformer模型如BERT不同,LLM的activations很难量化。当我们将LLM扩展到超过6.7B参数时,activations中会涌现系统性的大幅值的异常值(《Llm.int8(): 8-bit matrix multiplication for transformers at scale》),导致较大的量化误差和精度下降。ZeroQuant应用了group-wise weight quantization和动态的per-token activation quantization(参考Figure 3)。它可以高效地实现,并为GPT-3-350M和GPT-J-6B提供良好的准确率。但是,它无法为具有175B参数的大型OPT模型维持准确率。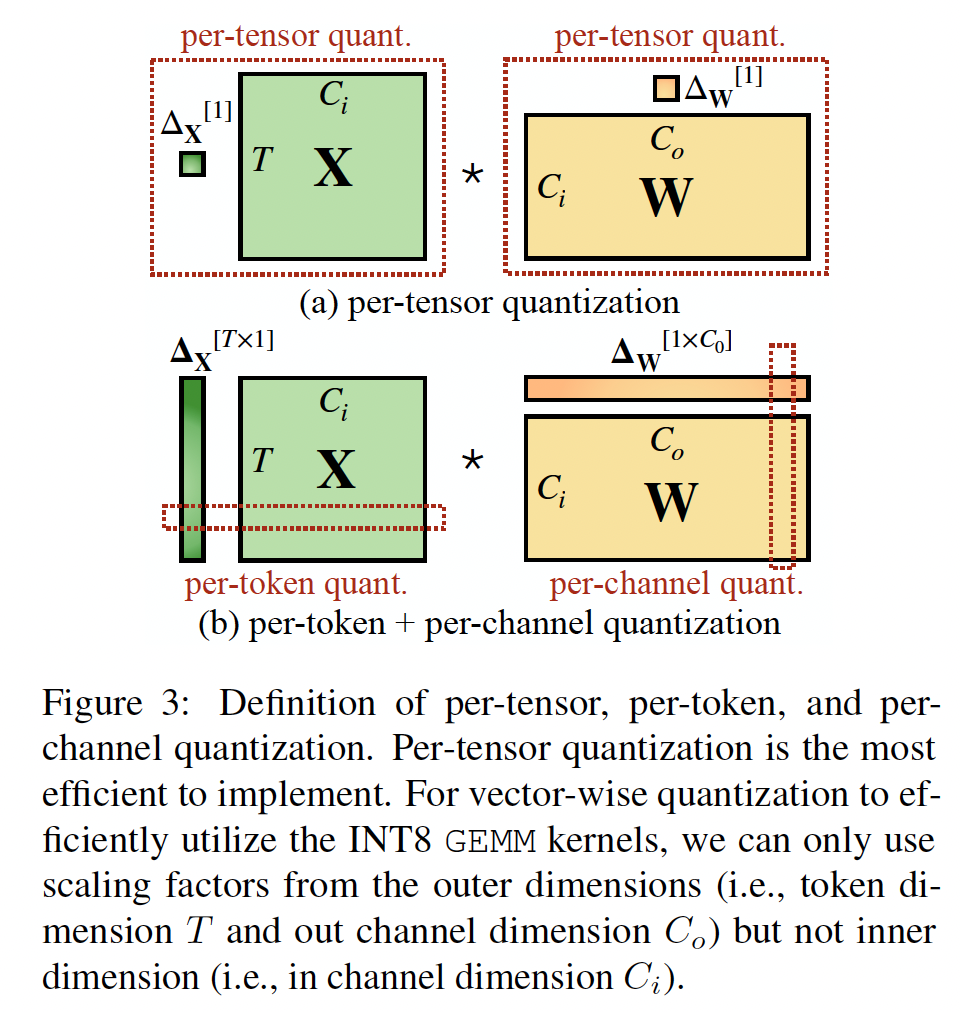
LLM.int8()通过进一步引入混合精度分解(即它将异常值保持为FP16,其他activations使用INT8)来解决该准确率问题。但是,在hardware accelerators上高效地实现该分解很困难。
因此,为
LLM派生出一种高效的、硬件友好的、最好不需要训练的量化方案,该方案会对所有计算密集型操作使用INT8,仍是一个开放性挑战。我们提出了
SmoothQuant,这是一种准确的、高效的后训练量化(post-training quantization: PTQ)解决方案从而用于LLM。SmoothQuant依赖于一个关键观察:由于存在异常值,即使activations比权重更难量化,不同tokens在其channels上表现出类似的变化。基于此观察,SmoothQuant离线地将quantization difficulty从activations迁移到权重(Figure 2)。SmoothQuant提出了一种数学等价的per-channel scaling transformation,可以显著平滑通道间的幅值,使模型对量化更加友好。由于SmoothQuant兼容各种量化方案,我们为SmoothQuant实现了三种效率级别的quantization setting(见Table 2的O1-O3)。实验表明,SmoothQuant具有硬件效率:它可以维持OPT-175B、BLOOM-176B、GLM-130B和MT-NLG 530B的性能,在PyTorch上获得高达1.51倍的加速和1.96倍的内存节省。SmoothQuant易于实现。我们将SmoothQuant集成到FasterTransformer中(这是SOTA的transformer serving框架),与FP16相比,实现了高达1.56倍的加速,以及内存占用减半。值得注意的是,相比较于FP16,SmoothQuant允许仅使用一半GPU数量就可以serving像OPT-175B等大型模型,而且更快,并可以在单个8-GPU节点上部署530B模型。我们的工作通过提供一键解决方案来减少serving成本,推广了LLM的使用。我们希望SmoothQuant可以在未来激发LLM的更广泛应用。注意:
SmoothQuant-O1/O2/O3对权重均采用per-tensor量化,区别仅在于activations上的量化方式。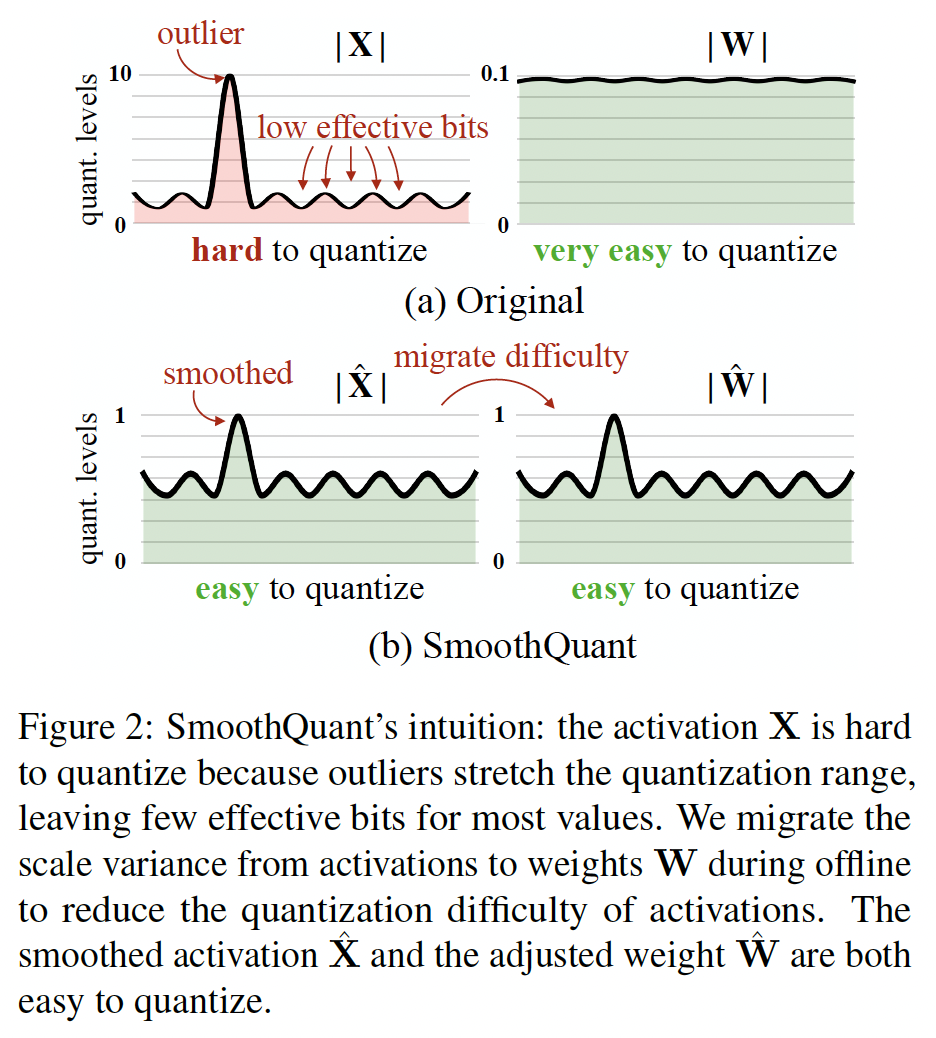

相关工作:
大型语言模型:通过
scaling up,pre-trained语言模型在各种基准测试中实现了显着的性能。GPT-3是首个超过100B参数的LLM,并在few-shot/zero-shot learning中取得了令人印象深刻的结果。后续工作继续推进scaling的前沿,超过了500B参数。但是,随着语言模型变大,为这些模型提供推理变得昂贵和具有挑战性。在本文中,我们展示了所提出的方法可以量化三个最大的开源LLM(OPT-175B、BLOOM-176B和GLM-130B),甚至MT-NLG 530B,以减少内存成本和加速推理。模型量化:量化是减小模型规模和加速推理的有效方法。它对各种卷积神经网络和
transformer都被证明是有效的。weight equalization(《Data-free quantization through weight equalization and bias correction》)和channel splitting(《Improving neural network quantization without retraining using outlier channel splitting》)通过抑制权重中的异常值来减小量化误差。但是,这些技术无法解决activation outliers,这是LLM量化的主要瓶颈(《Llm.int8(): 8-bit matrix multiplication for transformers at scale》)。LLM的量化:《Gptq: Accurate post-training quantization for generative pretrained transformers》仅对权重而不是activations进行量化(请参阅附录A的简短讨论)。ZeroQuant(《Zeroquant: Efficient and affordable post-training quantization for large-scale transformers》)和nuQmm(《nuqmm: Quantized matmul for efficient inference of large-scale generative language models》)为LLM使用per-token(在activations上)和group-wise(在weights上)的量化方案,需要定制的CUDA kernels。它们分别评估的最大模型为20B和2.7B,未能维持OPT-175B等LLM的性能。LLM.int8()(《Llm.int8(): 8-bit matrix multiplication for transformers at scale》)使用混合INT8/FP16 decomposition来处理activation outliers。但是,这样的实现导致很大的延迟开销,甚至比FP16推理更慢。在
6.7B及其以上规模的模型中,LLM.int8()的推理速度比FP16更快;而更小规模的模型中,LLM.int8()反而更慢。Outlier Suppression(《Outlier suppression: Pushing the limit of low-bit transformer language models》)使用non-scaling Layer-Norm和token-wise clipping来处理activation outliers。但是,它只在小型语言模型(如BERT和BART)上成功,未能维持LLM的准确率(Table 4)。
我们的算法以高效的
per-tensor的、静态的量化方案保留了LLM的性能(高达176B,我们能找到的最大的开源LLM),而无需重新训练,允许我们使用开箱即用的INT8 GEMM来实现高的硬件效率。从
Table 4可以看到,LLM.int8()的效果相当好,和表现最佳的SmoothQuant相比相差无几甚至更好。而且在175B模型上,LLM.int8()的推理速度可以高达2倍(相比于FP16)。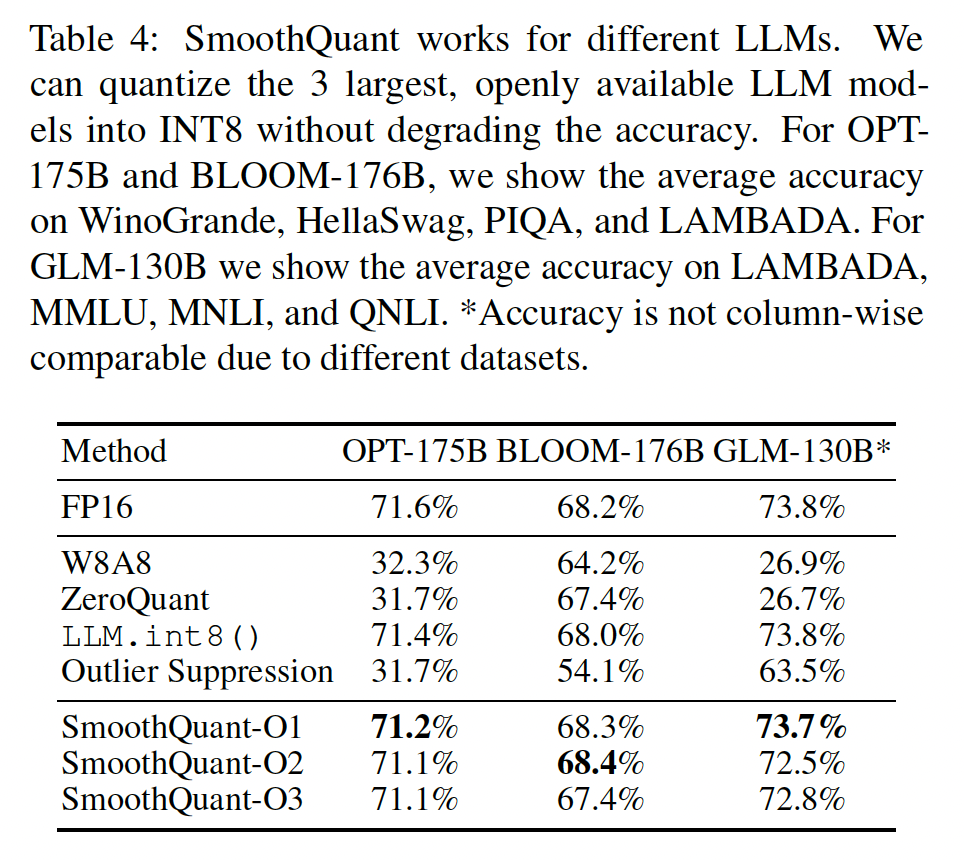
5.1 背景知识
量化将一个
high-precision value映射到离散级别(discrete levels)。我们研究整数(具体为INT8)的uniform quantization(《Quantizationand training of neural networks for efficient integer arithmetic-only inference 》)以获得更好的硬件支持和效率。量化过程可以表示为:其中:
quantization step size),rounding函数,bits数量(在我们这个case中是8)。
这里为简单起见,假设张量
ReLU非线性函数之后),通过添加一个zero-point,讨论过程是类似的(《Quantization and training of neural networks for efficient integer arithmetic-only inference》)。这样的量化器(
quantizer)使用maximum absolute value来计算activation中的异常值,这些异常值对精度很重要(《Llm.int8(): 8-bit matrix multiplication for transformers at scale》)。我们可以用一些
calibration samples的activations来离线地计算static quantization)。我们也可以使用
activations的运行时统计信息(runtime statistics)得到dynamic quantization)。
如
Figure 3所示,量化具有不同的粒度级别:per-tensor quantization对整个矩阵使用单个步长。通过为每个
token相关联的activations((per-token quantization)、或权重的每个output channel相关联的activations(per-channel quantization)使用不同的量化步长,我们可以实现更细粒度的量化。per-channel quantization的一个粗粒度版本是对不同的channel groups使用不同的量化步长,称为group-wise quantization(《Q-bert: Hessian based ultra low precision quantization of bert》、《Zeroquant: Efficient and affordable post-training quantization for large-scale transformers》)。
通俗地讲:
per-tensor量化:对矩阵(权重矩阵或者activation矩阵)采用单个步长。per-channel量化:对权重矩阵按列量化,即每一列对应一个步长。per-token量化:对activation矩阵按行量化,即每一行对应一个步长。

对于
transformer中的线性层(参见Figure 3,为简单起见,我们省略了batch维度):其中:
input activations,token数量,output activations。
通过将权重量化为
INT8,相比FP16,我们可以将模型存储量减半。但是,为了加速推理,我们需要将权重和activations都量化为INT8(即W8A8),从而利用integer kernels(如INT8 GEMM),这些integer kernels被广泛的硬件所支持(如NVIDIA GPU、Intel CPU、Qualcomm DSP等)。
5.2 回顾 Quantization Difficulty
由于
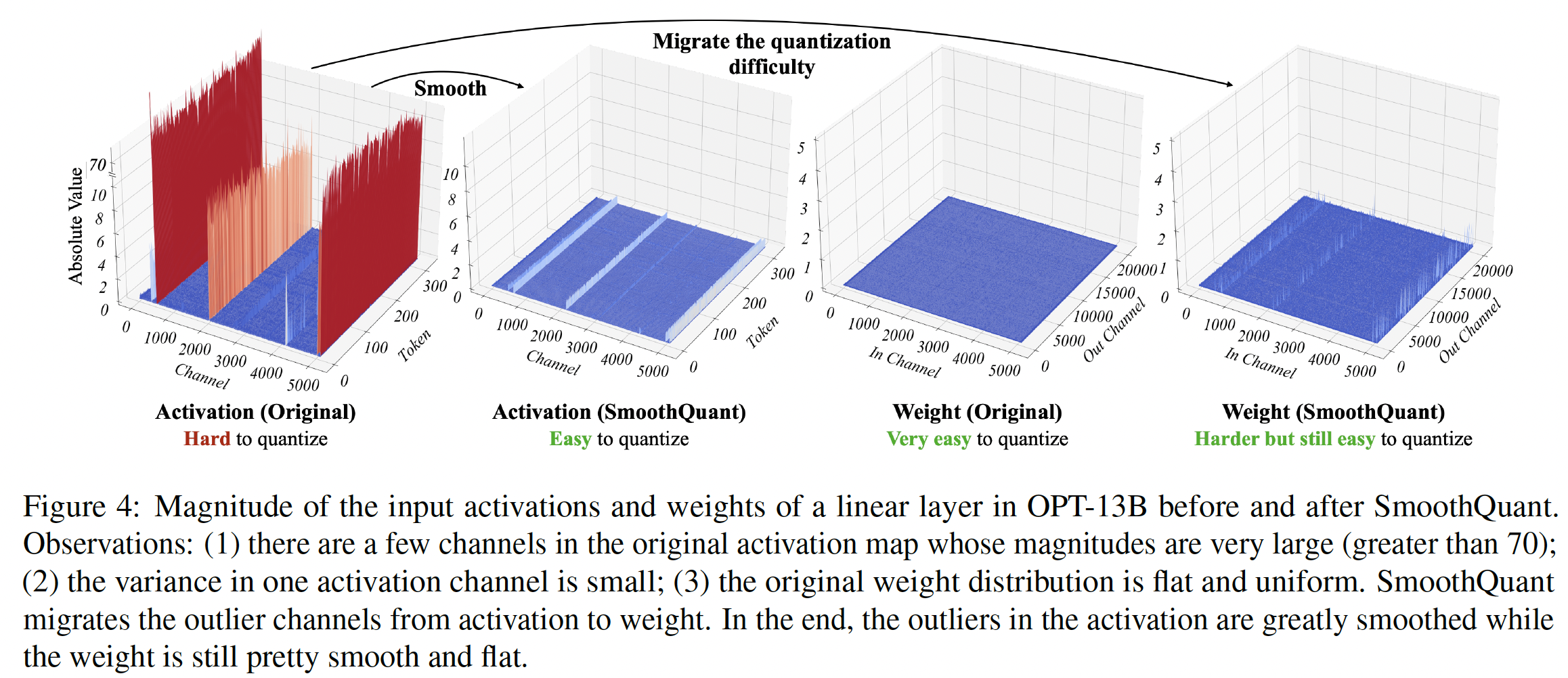
activations中的异常值,LLM难以量化。我们首先回顾activation quantization的困难,并在异常值中寻找模式。我们在Figure 4(Left)中可视化了具有较大quantization error的线性层的input activations和权重。我们可以找到几个启发我们方法的模式:(1):activations比权重更难量化。权重分布非常均匀和平坦,很容易量化。先前的工作表明,使用
INT8甚至INT4来量化LLM的权重,不会降低准确性,这与我们的观察一致。(2):异常值使activation quantization困难。activation中的异常值的scale比大多数activations大约高100倍。在per-tensor quantization的情况下,large outliers主导maximum magnitude的测量,导致non-outlier channels的effective quantization bits/levels较低(Figure 2):假设通道maximum magnitude为effective quantization levels为non-outlier channels,effective quantization levels将非常小(2-3),导致较大的量化误差。即,在
non-outlier channels上,量化后的结果都聚集在少数的bins上,导致逆量化之后都集中在少数几个值上。(3):异常值出现在固定的通道中。对于
activations,异常值仅出现在少数通道中。如果一个通道有一个异常值,它会持续出现在所有tokens中(Figure 4,红色)。给定一个
token,它的各个通道之间的activations方差很大(某些通道中的activations非常大,但大多数很小)。但给定一个通道,它的跨
tokens之间的activations方差很小(异常值通道中的activations一致地很大)。
由于异常值的
persistence、以及每个通道内的小方差,如果我们可以对activation进行per-channel quantization(《Understanding and overcoming the challenges of efficient transformer quantization》)(即对每个通道使用不同的量化步长),与per-tensor quantization相比,量化误差会小得多,而per-token quantization几乎没有帮助。在Table 1中,我们验证了假设:模拟的per-channel activation quantization成功地与FP16 baseline实现了准确率一致。这与《Understanding and overcoming the challenges of efficient transformer quantization》的发现一致。对于
activations,per-token quantization就是按行进行量化,per-channel quantization就是按列进行量化。为什么说这里是 “模拟” 的?因为目前的硬件不支持
activations的per-channel quantization,因此作者采用模拟的手段来实现相同的效果。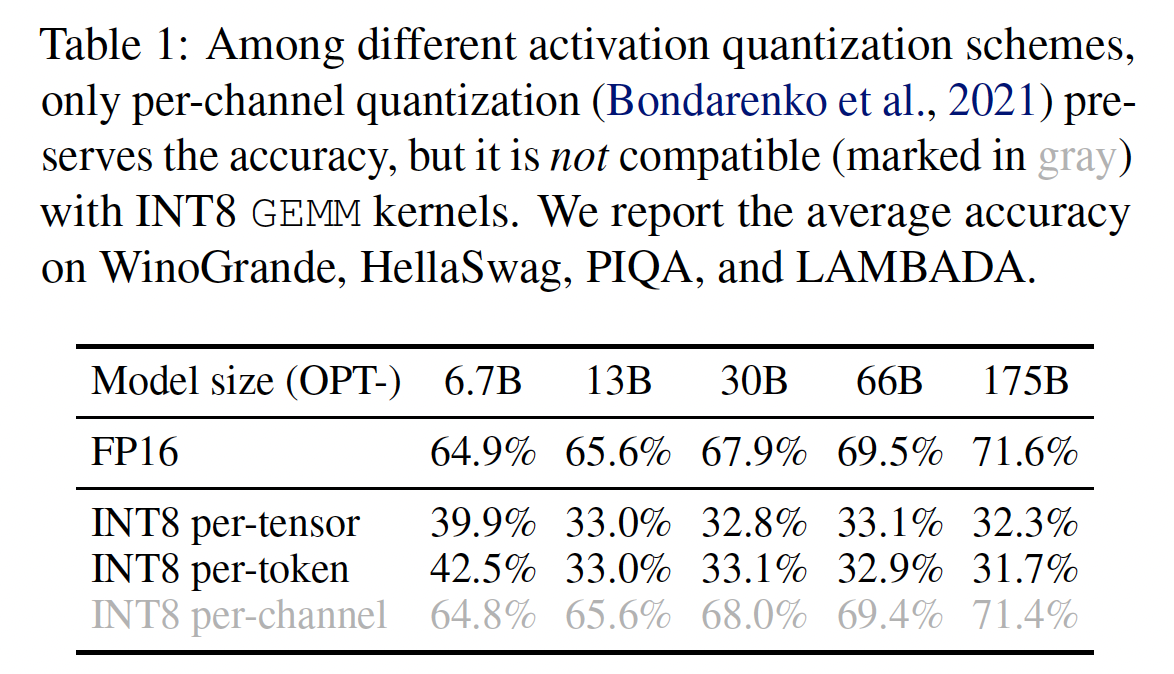
然而,
per-channel activation quantization与硬件加速的GEMM kernels不匹配,这些GEMM kernels依赖于高吞吐量地执行的a sequence of operations(如Tensor Core MMAs) ,并且不容忍在该序列中插入吞吐量较低的指令(例如,转换、或CUDA Core FMAs)。在这些kernels中,scaling只能沿矩阵乘法的outer dimensions执行(即activations的token dimensionoutput channel dimensionFigure 3)。这种scaling通过在矩阵乘法完成后应用如下操作来实现:其中:
activations和权重。因此,先前的工作都为线性层使用
per-token activation quantization(Llm.int8(), Zeroquant),尽管它们无法解决activation quantization的困难(仅比per-tensor quantization量略好)。
5.3 SmoothQuant
我们提出平滑
input activation而不是执行per-channel activation quantization(这不可行),方法是将input activation除以per-channel smoothing factor其中:
即,对
activation矩阵的第考虑到输入
linear layers、layer norms等),我们可以轻松地将平滑因子(smoothing factor)离线地融合到前一层的参数中,这不会导致an extra scaling的kernel call的开销。对于其他一些情况,当输入residual add时,我们可以像《Outlier suppression: Pushing the limit of low-bit transformer language models》那样,在residual branch中添加an extra scaling。关于如何融合平滑因子,可以参考论文的实现代码。
将
quantization difficulty从activations迁移到权重:我们的目标是选择per-channel smoothing factoreffective quantization bits。当所有通道具有相同的maximum magnitude时,total effective quantization bits将最大。因此,一个直观的选择是:其中
这种选择确保在除法之后,所有
activation channels将具有相同的最大值,很容易量化。注意,activations的范围是动态的;它对不同的输入样本各不相同。这里,我们使用预训练数据集中的calibration samples来估计activations channels的scale(《Quantization and training of neural networks for efficient integer arithmetic-only inference》)。然而,这个公式将所有
quantization difficulty都推到权重上。我们发现,在这种情况下,权重的量化误差会很大(outlier channels现在迁移到权重上),导致很大的准确率下降(参见Figure 10)。
另一方面,我们也可以通过选择
quantization difficulty从权重推到activations。类似地,由于activation量化误差,模型性能不佳。因此,我们需要在权重和activations之间分担quantization difficulty,以使它们都易于量化。这里我们引入一个超参数,迁移强度(
migration strength)activations迁移到权重的难度量,使用以下等式:我们发现,对于大多数模型(例如所有的
OPT和BLOOM模型),quantization difficulty,尤其是在我们对权重和activations使用相同的quantizer时(例如per-tensor的静态量化)。该公式确保权重和activations在相应的通道上共享相似的最大值,因此共享相同的quantization difficulty。Figure 5说明了当我们取smoothing transformation。 对于activation outliers更明显的一些其他模型(例如GLM-130B有约30%的异常值,这对activation quantization更具挑战性),我们可以选择较大的quantization difficulty迁移到权重(如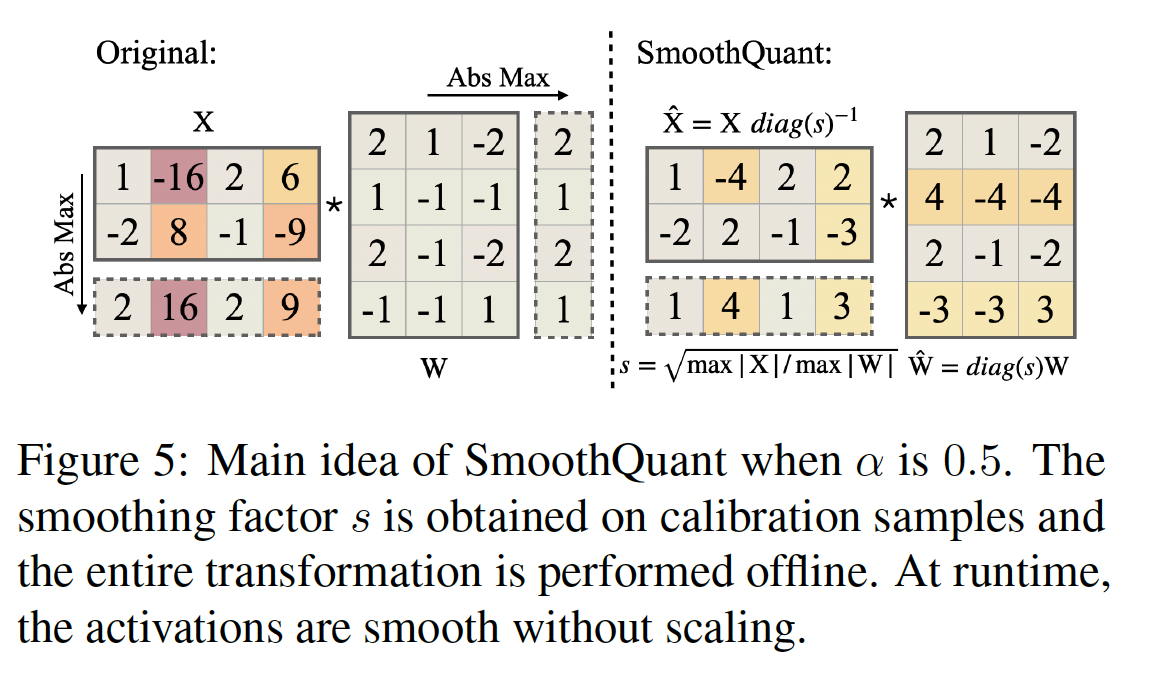
将
SmoothQuant应用于Transformer blocks:线性层占了LLM模型的参数和计算的大部分。默认情况下,我们对自注意力和前馈层的input activations执行scale smoothing,并使用W8A8量化所有线性层。我们还量化注意力计算中的BMM算子。我们在Figure 6中设计了transformer模块的量化流程。我们使用INT8 quantization计算compute-heavy的算子(如线性层和注意力层中的BMM)的输入和权重,而将其他轻量级element-wise算子(如ReLU、Softmax和Layer-Norm)的activation保持为FP16。这种设计帮助我们在精度和推理效率之间取得平衡。BMM:batch的matrix-matrix乘法。
5.4 实验
baselines:我们在INT8 post-training quantization setting(即,不重训模型参数)中与四个基准进行比较:W8A8 naive quantization、ZeroQuant、LLM.int8()、Outlier Suppression。由于
SmoothQuant与量化方案正交,我们提供从O1到O3逐渐激进的和有效的quantization levels。基准和SmoothQuant的详细量化方案如Table 2所示。
模型和数据集:
我们选择三个
LLM系列来评估SmoothQuant:OPT、BLOOM和GLM-130B。我们使用七个
zero-shot evaluation tasks:LAMBADA、HellaSwag、PIQA、WinoGrande、OpenBookQA、RTE、COPA,以及一个语言建模数据集WikiText来评估OPT和BLOOM模型。我们使用
MMLU、MNLI、QNLI和LAMBADA来评估GLM-130B模型,因为上述一些基准出现在GLM-130B的训练集中。我们使用
lm-eval-harness来评估OPT和BLOOM模型,使用GLM-130B的官方仓库评估其本身。最后,我们将方法扩展到
MT-NLG 530B,首次在单节点内实现了对大于500B模型的serving。
注意,我们关注量化前后模型的相对性能变化而不是绝对值变化。
Activation smoothing:迁移强度OPT和BLOOM模型的通用最佳点;而对于量化更具挑战性的activations的GLM-130B,Pile验证集的一个子集上快速grid search以获得合适的activations的统计信息,我们一次性地使用预训练数据集Pile中的512个随机句子,从而校准smoothing factors和static quantization step sizes,并将相同的smoothed and quantized model应用于所有下游任务。通过这种方式,我们可以benchmark量化后的LLM的普适性和zero-shot性能。实现:我们使用两个后端实现
SmoothQuant:(1):PyTorch Huggingface进行概念验证。(2):FasterTransformer作为生产环境中使用的高性能框架的示例。
在
PyTorch Huggingface和FasterTransformer框架中,我们都使用CUTLASS INT8 GEMM kernels实现了INT8线性模块和batched matrix multiplication: BMM函数。我们简单地用我们的INT8 kernels替换原始的浮点(FP16)线性模块和bmm函数,从而作为INT8模型。
5.4.1 准确的量化
OPT-175B的结果:SmoothQuant可以处理非常大的LLM的量化,其中,这种大型LLM的activations更难以量化。我们在OPT-175B上研究量化。如Table 3所示:SmoothQuant可以在所有评估数据集上在所有量化方案上匹配FP16的准确率。LLM.int8()可以匹配浮点的准确率,因为他们使用浮点值来表示异常值,这会导致很大的延迟开销(Table 10)。W8A8、ZeroQuant和Outlier Suppression等baselines产生几乎随机的结果,表明朴素地量化LLM的activation将破坏性能。
在这三种
SmoothQuant变体中,SmoothQuant-O3的实现最简单(静态的per-tensor量化),但是效果也还不错。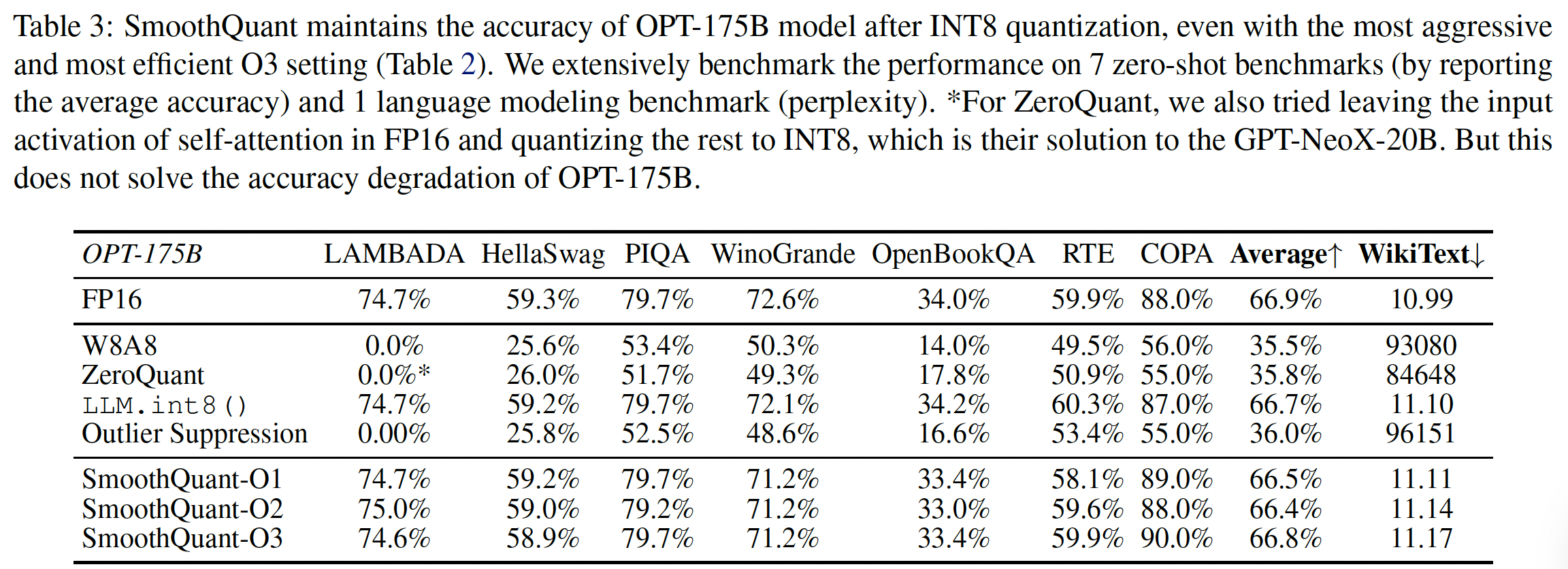
不同
LLM的结果:SmoothQuant可以应用于各种LLM。在Table 4中,我们展示SmoothQuant可以量化所有现有的超过100B参数的开源LLM。与
OPT-175B模型相比,BLOOM-176B模型更容易量化:没有baselines完全破坏模型;即使是朴素的W8A8 per-tensor dynamic quantization也只降低了4%的准确率。SmoothQuant的O1-level和O2-level成功地维持了浮点的准确率,而O3-level(per-tensor static)降低了平均准确率0.8%,我们将其归因于统计信息与真实评估样本activation statistics之间的差异。相反,
GLM-130B模型更难以量化(《Glm-130b: An open bilingual pre-trained model》相呼应)。尽管如此,SmoothQuant-O1可以匹配FP16的准确率,而SmoothQuant-O3的准确率只降低了1%,明显优于baselines。注意,在为GLM-130B校准static quantization step sizes时,我们按照《Outlier suppression: Pushing the limit of low-bit transformer language models》的方法裁剪了top 2% tokens。
注意,不同的模型/训练设计具有不同的
quantization difficulty,我们希望这能激发未来的研究。注意:对于给定的量化方法,即使它在某个大模型上表现较好,也无法断定它在另一些大模型上表现也好。例如,
ZeroQuant在BLOOM-176B上表现较好,但是在OPT-175B上表现很差。
不同大小的
LLM的结果:SmoothQuant不仅适用于超过100B参数的非常大的LLM,而且也适用于较小的LLM。在Figure 7中,我们展示SmoothQuant可以适用于所有规模的OPT模型,使用INT8 quantization匹配FP16的准确率。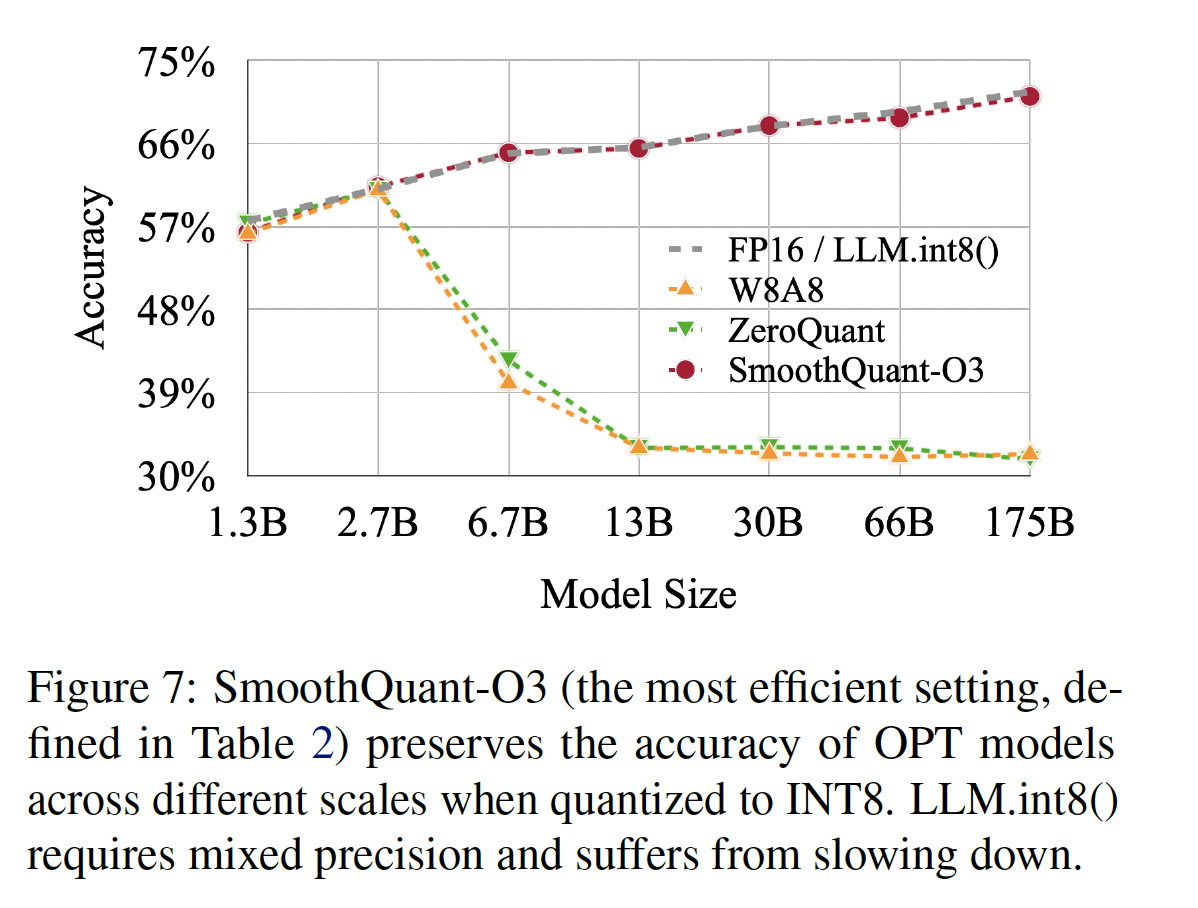
Instruction-Tuned LLM的结果:如Table 5所示,SmoothQuant也适用于Instruction-Tuned LLM。我们在OPT-IML-30B模型上使用WikiText-2和LAMBADA数据集测试SmoothQuant。我们的结果表明:SmoothQuant成功地以W8A8 quantization保留了模型准确率,而baselines未能做到这一点。SmoothQuant是为transformer模型平衡quantization difficulty而设计的通用方法。由于Instruction-Tuned LLM的架构与普通LLM在本质上没有不同,它们的预训练过程也非常相似,因此SmoothQuant也适用于Instruction-Tuned LLM。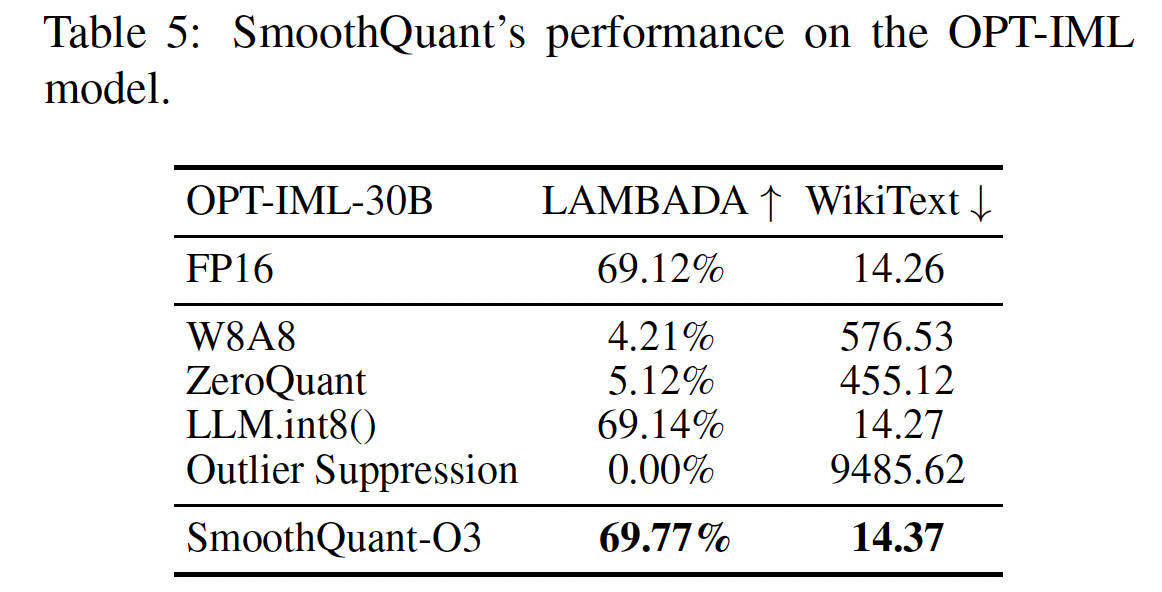
LLaMA模型的结果:LLaMA模型是具有卓越性能的新的开源语言模型。通过初步实验,我们发现:与OPT和BLOOM等模型相比,LLaMA模型通常具有更轻度的activation outlier问题。尽管如此,SmoothQuant对LLaMA模型仍然非常有效。我们在Table 6中给出了LLaMA W8A8 quantization的一些初步结果。W8A8 SmoothQuant的性能与FP16 baseline相差无几。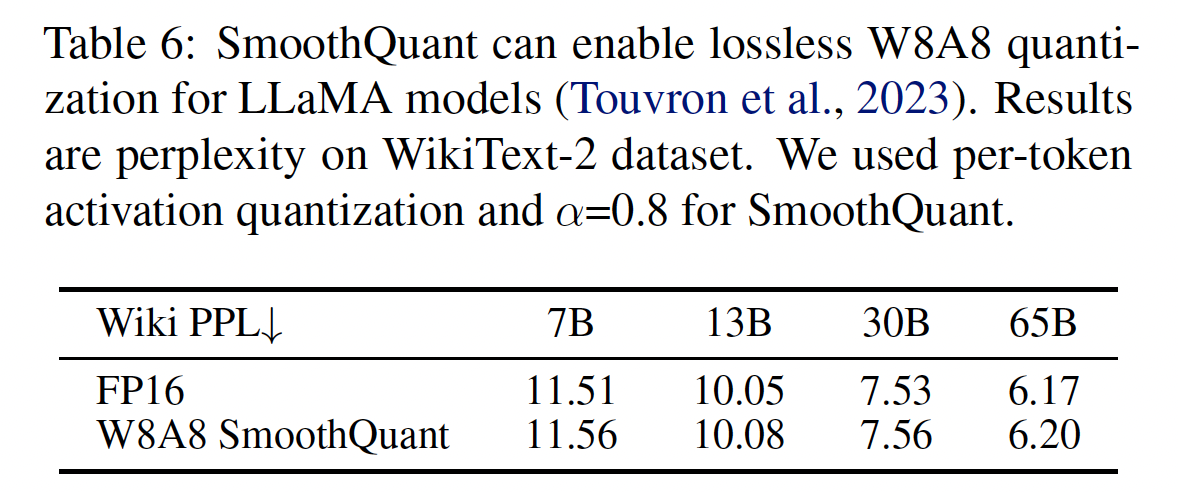
5.4.2 加速和内存节省
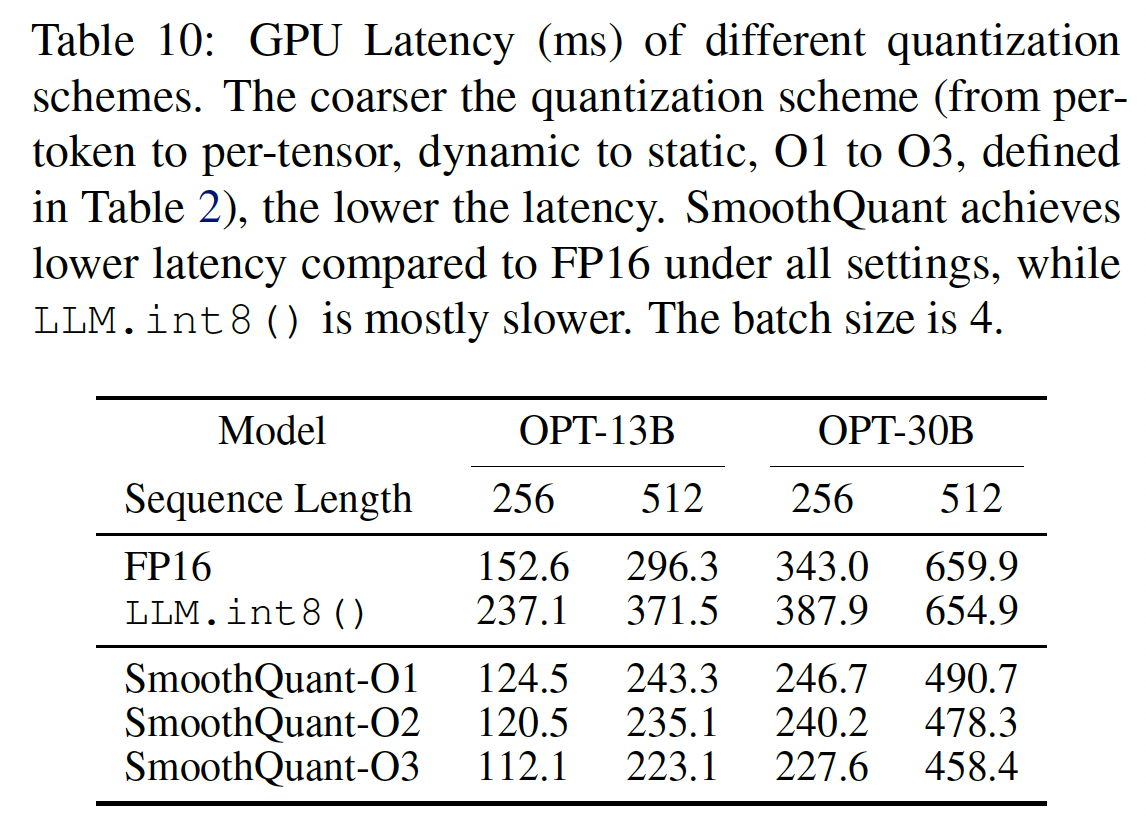
在这一节中,我们展示了集成到
PyTorch和FasterTransformer中的SmoothQuant-O3所测量到的加速和内存节省。Context-stage: PyTorch Implementation:针对a batch of 4 sentences,我们测量在one pass中生成所有隐状态的端到端延迟,即上下文阶段延迟(context stage latency)。我们记录此过程中的(聚合后的)峰值GPU内存使用。我们仅将SmoothQuant与LLM.int8()进行比较,因为后者是唯一可以在所有规模上保持LLM准确率的现有量化方法。由于
Huggingface不支持模型并行,针对PyTorch实现,我们只在单GPU上测量SmoothQuant的性能,因此我们选择OPT-6.7B、OPT-13B和OPT-30B进行评估。在
FasterTransformer库中,SmoothQuant可以与张量并行算法无缝协作,所以我们同时针对单GPU和多GPU基准测试,在OPT-13B、OPT-30B、OPT-66B和OPT-175B上测试SmoothQuant。我们的所有实验都是在
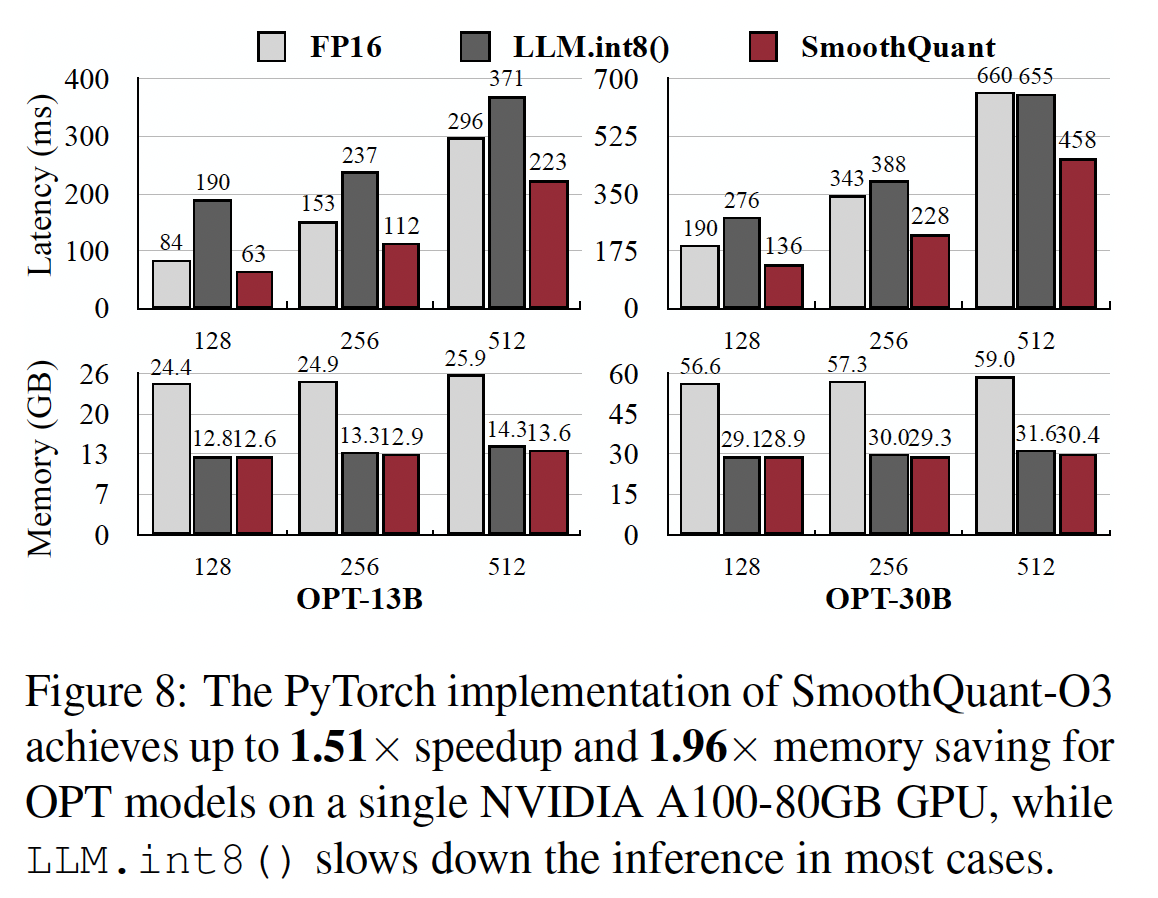
NVIDIA A100 80GB GPU服务器上进行的。Figure 8显示了基于PyTorch实现的inference latency和峰值内存使用。可以看到:SmoothQuant始终比FP16 baseline更快,在序列长度为256时,在OPT-30B上获得了1.51倍的加速。我们还看到,模型越大,加速越明显的趋势。另一方面,
LLM.int8()几乎总是比FP16 baseline慢,这是由于mixed-precision activation representation的大开销。在内存方面,
SmoothQuant和LLM.int8()都将FP16模型的内存使用减少了近一半,而SmoothQuant节省的内存略多,因为它使用fully INT8 GEMMs。
Context-stage: FasterTransformer Implementation:如Figure 9 (top)所示,与OPT的FasterTransformer's FP16实现相比,SmoothQuant-O3可以将单GPU上,将OPT-13B和OPT-30B的执行延迟降低最多1.56倍。这具有挑战性,因为与PyTorch实现相比,FasterTransformer的OPT-30B已经快了3倍以上。值得注意的是,对于必须跨多个
GPU分配的更大模型,SmoothQuant使用仅一半数量的GPU(对于OPT-66B,只需要1个GPU而不是2个;对于OPT-175B,只需要4个GPU而不是8个)实现了类似甚至更好的延迟。这可以大大降低serving LLM的成本。Figure 9 (bottom)显示,在FasterTransformer中使用SmoothQuant-O3时所需的内存减少了近2倍。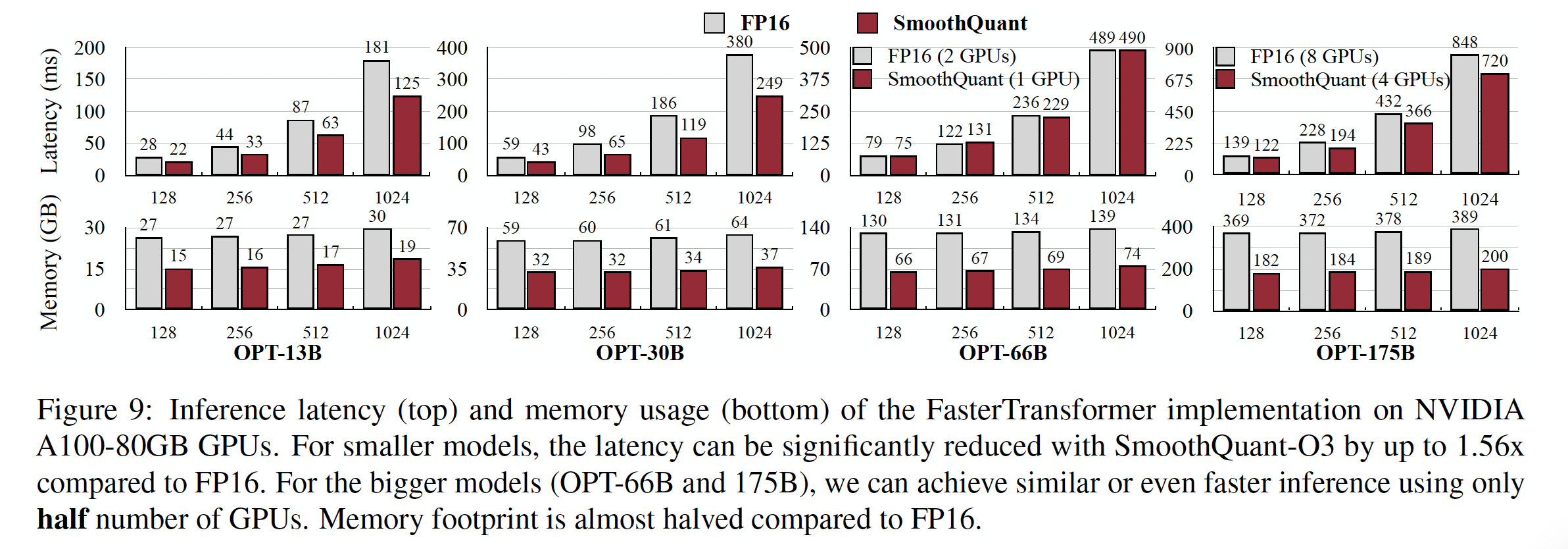
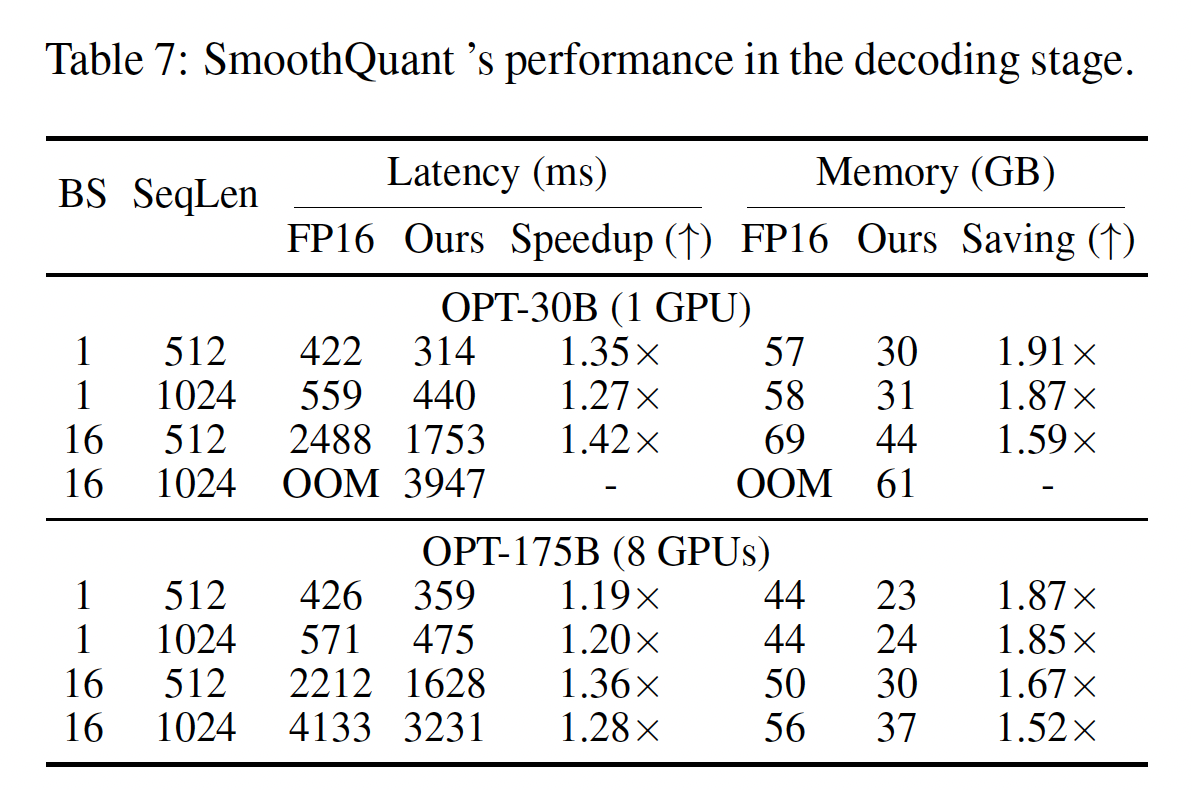
Decoding-stage:在Table 7中,我们展示SmoothQuant可以显著加速LLM的自回归解码阶段。与
FP16相比,SmoothQuant一致地降低per-token decoding延迟(最高1.42倍加速)。此外,
SmoothQuant将LLM推理的内存占用减半,使LLM部署的成本大大降低。
5.4.3 Scaling Up: 单节点内的 530B 模型
我们可以进一步将
SmoothQuant扩展至超过500B级别的模型,实现MT-NLG 530B的高效的和准确的W8A8 quantization。如Table 8和Table 9所示,SmoothQuant实现了530B模型在可忽略的准确率损失下的W8A8 quantization。减小的模型大小允许我们使用一半数量的GPU(从16 GPU到8 GPU)来serve模型,在类似延迟下,实现了单节点(8 * A100 80 GPU)内serving大于500B模型。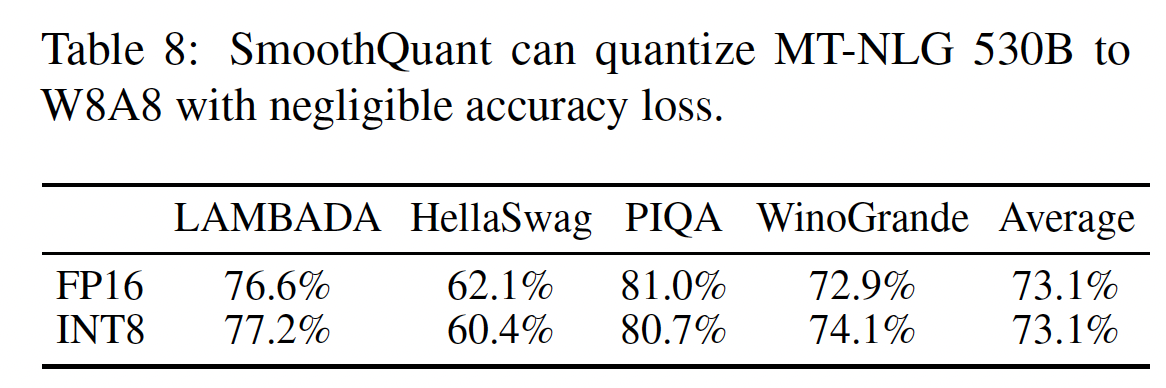
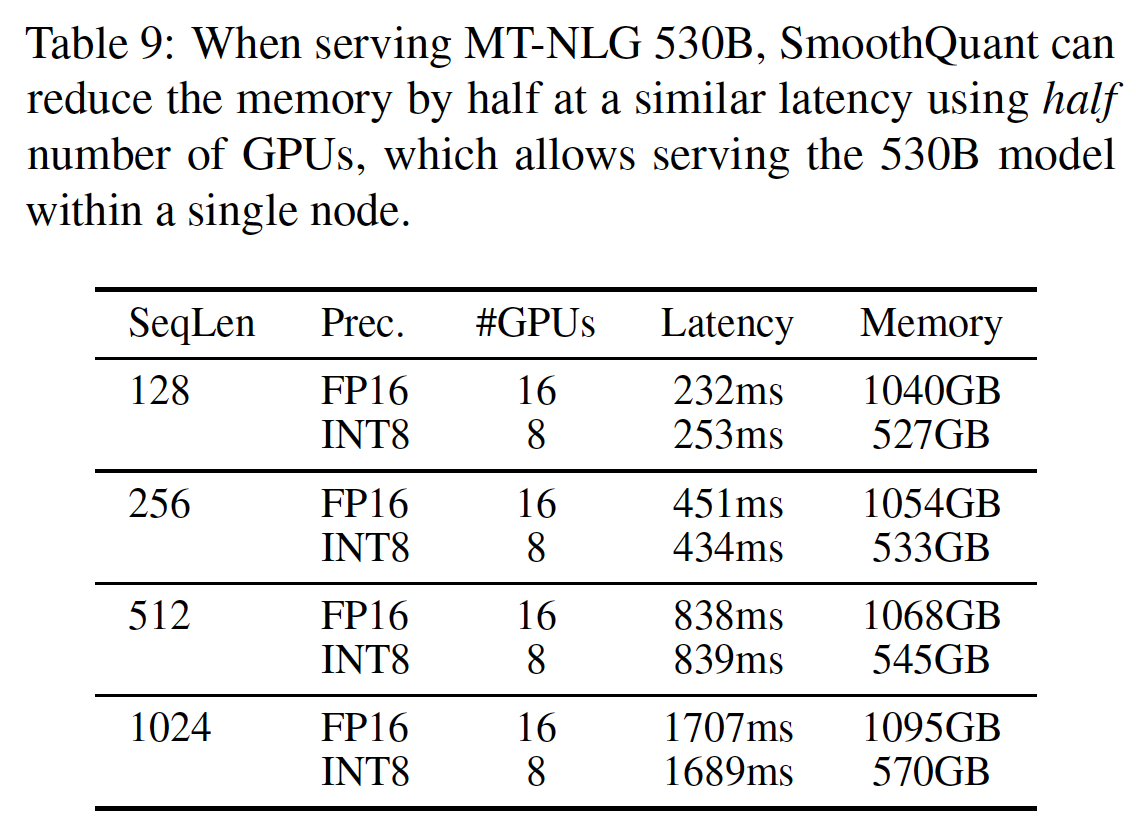
5.4.4 消融实验
量化方案:
Table 10基于我们的PyTorch实现显示了不同量化方案的inference latency。我们可以看到:量化粒度越粗(从
O1到O3),延迟越低。静态量化与动态量化相比可以显著加速推理,因为我们不再需要在运行时计算量化步长。
SmoothQuant在所有设置下都比FP16 baseline快,而LLM.int8()通常更慢。
如果准确率允许,我们建议使用更粗粒度的方案。

迁移强度:我们需要找到合适的迁移强度
activations之间的quantization difficulty。我们在Figure 10中检验不同OPT-175B和LAMBADA的影响。当
0.4)时,activations难以量化。当
0.6)时,权重难以量化。只有当我们从最佳区域(
0.4 ~ 0.6)选择activations的小的量化误差,并在量化后保持模型性能。

六、GPTQ [2022]
论文:
《GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers》
来自
Transformer家族的pretrained生成式模型(如GPT或OPT),在复杂的语言建模任务中展示了突破性的性能,导致了人们巨大的学术的和实际的兴趣。它们的一个主要障碍是计算成本和存储成本,这些成本在已知模型中是最高的。例如,性能最佳的模型变种,即GPT3-175B,参数量级达175B,需要数十到数百个GPU years才能训练(《OPT: Open pre-trained transformer language models》)。即使是在更简单的任务,即在pre-trained模型上进行推理,也非常具有挑战性(这也是我们在本文中关注的焦点):例如,GPT3-175B的参数以compact float16 format存储时,占用326GB(以1024为基数计算)的内存。这甚至超过了最高端的single GPU的容量,因此推理必须使用更复杂的和更昂贵的setup来执行,例如multi-GPU deployments。尽管消除这些开销的标准方法是模型压缩,例如
《Sparsity indeep learning: Pruning and growth for efficient inference and training in neural networks》、《A survey of quantization methods for efficient neural network inference》,但令人惊讶的是,几乎没有人知道如何压缩这些模型以进行推理。一个原因是,针对low-bit width quantization或model pruning的更复杂的方法通常需要对模型进行重新训练,而这对于十亿级参数的模型来说极其昂贵。另一方面,在不进行重新训练的情况以one shot方式压缩模型的post-training方法非常有吸引力。不幸的是,这种方法的更accurate的变体非常复杂,很难扩展到十亿级的参数(《ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers》)。到目前为止,只有round-to-nearest quantization的basic variants(《LLM.int8(): 8-bit matrix multiplication for transformers at scale》)已经应用于GPT-175B规模;虽然这对low compression目标(例如,8-bit权重)而言效果很好,但它们在更高的压缩率下无法保持准确率。因此,one-shot post-training quantization到更高压缩率是否可行,仍然是个未解决问题。贡献:在本文中,我们提出了一种新的
post-training quantization方法GPTQ,其效率足以在几小时内对数百亿参数的模型执行,精度足以将这些模型压缩到每个参数3 bits或4 bits,几乎没有损失准确率。例如,GPTQ可以在大约4 GPU hours内量化最大的开源可用模型OPT-175B和BLOOM-176B,并且仅仅稍稍增加了困惑度(困惑度是非常严格的准确率指标)。此外,我们还表明,在极端量化区域,即模型被量化为每个参数
2 bits、甚至1.5 bits(即,该数据类型只有三个值),我们的模型也可以提供稳健的结果。在实用性方面,我们开发了一个执行工具,允许我们为生成式任务有效地执行被量化后的compressed models。具体来说,我们能够第一次在单个NVIDIA A100 GPU上运行compressed OPT-175B model,或者只使用两个更经济实惠的NVIDIA A6000 GPU来运行。我们还实现了定制的GPU kernels,能够利用compression进行更快的内存加载,在使用A100 GPU时加速了3.25倍、在使用A6000 GPU时加速了4.5倍。据我们所知,我们是首次展示含数百亿参数的
extremely accurate的语言模型可以被量化到每个参数3-4 bits:之前的post-training方法只能在8 bits下保持准确率(《ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers》、《LLM.int8(): 8-bit matrix multiplication for transformers at scale》);而之前的training-based的技术只处理过小一个到两个数量级的模型(《Extreme compression for pre-trained transformers made simple and efficient》)。这种高度压缩似乎很自然,因为这些网络是过参数化的(overparametrized);然而,正如我们在对结果的详细分析中所讨论的,compression在语言建模的准确率(即,困惑度指标)、bit-width、以及原始模型大小之间引入了重要的tradeoffs。我们希望我们的工作将激发这个领域的进一步研究,并且可以是进一步的步骤从而使这些模型更广泛可用。就局限性而言,我们的方法目前无法为实际乘法提供加速,因为主流架构上缺乏对混合精度操作数(例如,
FP16 * INT4)的硬件支持。此外,我们当前的结果不包括activation quantization,因为它们在我们的目标场景中不是关键瓶颈;然而,这可以使用正交技术来支持(《ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers》)。相关工作:量化方法大致分为两类:
quantization during training、post-training方法。前者在通常昂贵的重新训练和/或微调期间对模型进行量化,针对rounding操作使用某种approximate differentiation机制(《A survey of quantization methods for efficient neural network inference》、《A white paper on neural network quantization》)。相比之下,post-training方法(也叫做one-shot方法)使用较少的资源对trained模型进行量化,通常需要几千个数据样本和几个小时的计算。post-training方法对于大型模型特别有前景,因为对大型模型进行完整的模型训练甚至微调都非常昂贵。我们在这里关注这种场景。Post-training Quantization:大多数post-training方法都集中在视觉模型上。通常,accurate的方法通过量化单个layers或small blocks of consecutive layers来操作。AdaRound方法(《Up or down? Adaptive rounding for post-training quantization》)通过annealing一个惩罚项来计算data-dependent rounding,该项鼓励权重向对应于quantization levels的grid points移动。BitSplit(《Towards accurate post-training network quantization via bit-split and stitching》)使用residual error的squared error objective逐比特地构建quantized value,而AdaQuant(《Accurate post training quantization with small calibration sets》)基于直接估计进行direct optimization。BRECQ(《BRECQ: Pushing the limit of post-training quantization by block reconstruction》)在目标函数中引入Fisher信息,并联合优化单个residual block的layers。最后,
Optimal Brain Quantization: OBQ(《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》)将经典的Optimal Brain Surgeon: OBS二阶权值修剪框架(《Efficient second-order approximation for neural network compression》)推广到量化。OBQ逐个地量化权重,按quantization error的顺序,总是调整剩余权重。
虽然这些方法可以在几个
GPU hours内为最多100M参数的模型产生良好结果,但将其扩展到数量级更大的网络面临挑战。Large-model Quantization:随着BLOOM或OPT-175B等语言模型的开源发布,研究人员已经开始开发可负担的方法来压缩这种巨大的网络以进行推理。尽管所有现有的工作(ZeroQuan、LLM.int8()和nuQmm)都仔细选择了量化粒度,如vector-wise,但它们最终只是将权重舍入到最近(round weights to the nearest: RTN)的quantization level,从而为每个非常大的模型维持可接受的运行时间。ZeroQuant进一步提出了类似于AdaQuant的逐层知识蒸馏(layer-wise knowledge distillation),但它可以应用这种方法的最大模型只有1.3B参数。在这种规模下,ZeroQuant已经需要3小时的计算;而GPTQ在4小时内量化了大约100倍的模型。LLM.int8()观察到在少数feature dimensions中的activation outliers会破坏更大模型的量化,并提出通过以更高的精度来保持这些维度从而来解决这个问题。最后,
nuQmm为一种特定的binary-coding based量化方案开发了高效的GPU kernels。
与这些工作相比,我们表明:在大的
model scale上可以有效地实现一个明显更复杂的和更精确的quantizer。具体来说,在类似的准确率下,GPTQ将先前技术的压缩量提高了一倍以上。
6.1 背景知识
Layer-Wise Quantization:在high level,我们的方法遵循SOTA的post-training quantization方法的结构,逐层执行量化,为每一层解决相应的重构问题。具体而言,设layer input(对应于少量的quantized weightsfull precision layer output的平方误差最小化。形式上,这可以描述为:此外,与
《Up or down? Adaptive rounding for post-training quantization 》、《BRECQ: Pushing the limit of post-training quantization by block reconstruction》、《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》类似,我们假设quantization grid在过程开始前就固定好了,单个权重可以如《Accurate post training quantization with small calibration sets》、《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》中那样自由移动。quantization grid就是bit-width。例如,int-4量化的grid粒度就要比int-8量化的粒度更粗。Optimal Brain Quantization:我们的方法建立在最近提出的Optimal Brain Quanization: OBQ方法(《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》)的基础上,用于解决上面定义的layer-wise quantization问题。我们对OBQ方法进行了一系列重大修改,这使其可以扩展到大规模语言模型,提供了三个数量级以上的计算加速。为了帮助理解,我们首先简要概括一下原始的OBQ方法。OBQ方法的起点是观察到公式OBQ独立地处理每一行由于对应的目标函数是二次函数,其海森矩阵为
full-precision weights的集合,那么greedy-optimal的下一个要量化的权重(记做optimal update(记做这是核心思想。后面的内容都是针对该公式的计算速度和稳定性上的优化。
其中:
quantization grid上的nearest value。
OBQ使用这两个等式迭代地量化权重,直到full recomputations:其中:
该方法具有向量化实现,可以并行处理
GPU上在1小时内完全量化ResNet-50模型(25M参数),这与实现SOTA准确率的其他post-training方法的运行时间大致相当(《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》)。然而,OBQ对推导过程,对于给定的权重行
则通过泰勒展开公式:
其中:
为最小化
因此对于第
6.2 GPTQ 算法
Step 1: Arbitrary Order Insight:如前一节所述,OBQ以贪心的顺序来量化权重,即它总是选择当前引起的additional quantization error最小的权重。有趣的是,我们发现,虽然这种非常自然的策略的确似乎表现非常好,但与任意顺序(arbitrary order)来量化权重相比,其改进通常很小,尤其是在大型的、参数密集的层上。很可能是因为数量较少的、具有较大误差的quantized weights,与那些在量化过程接近结束时的quantized weights所平衡;而在量化过程接近结束时,只剩下很少其他unquantized weights可以进行补偿调整。正如我们现在要讨论的,这一见解,即任意固定顺序可能表现良好,特别是在大型模型上,具有有趣的影响。原始
OBQ方法独立地以特定顺序(该顺序由对应的additional quantization error来定义)量化final squared error。因此,unquantized weights的集合Figure 2中的示意图)。更具体地说,后者是由于layer input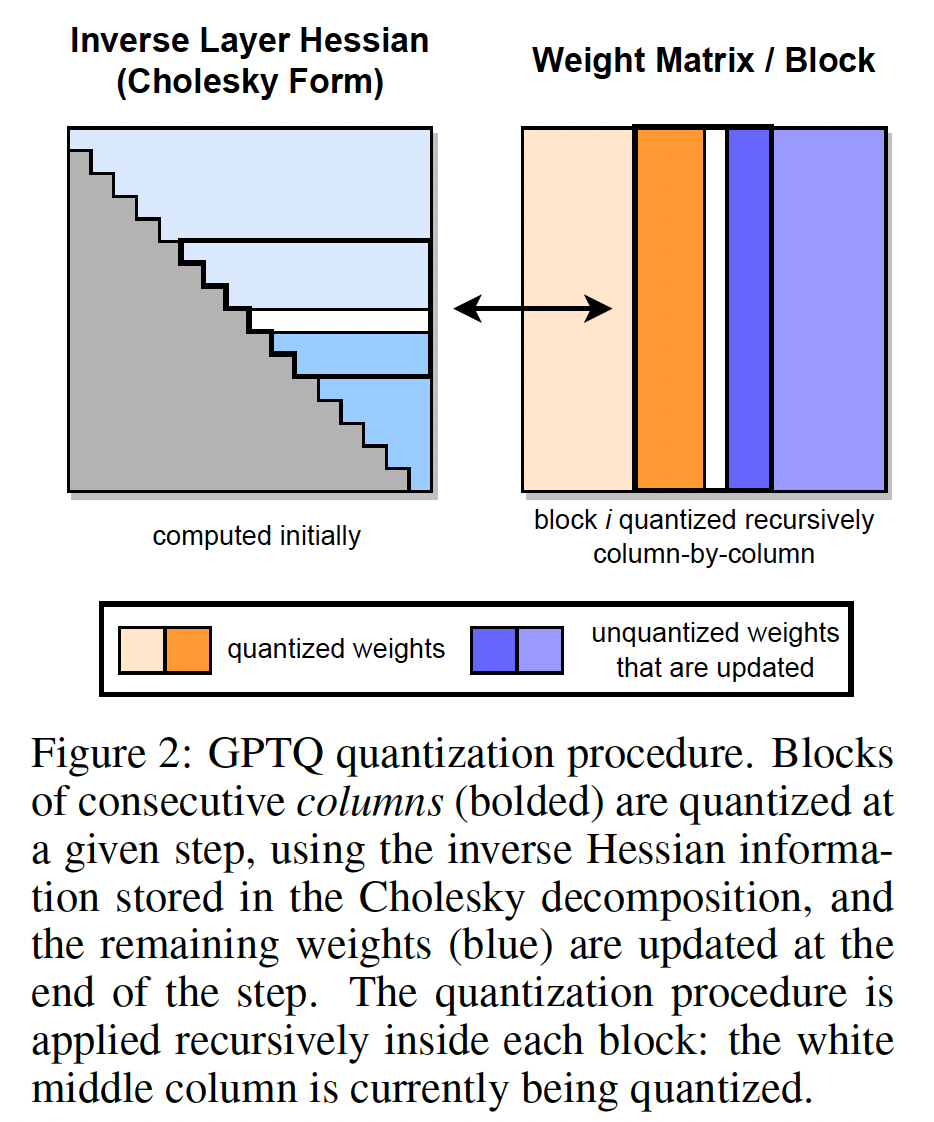
Step 2: Lazy Batch-Updates:首先,直接实现前面描述的方案在实践中将不会很快,因为该算法具有相对较低的compute-to-memory-access ratio。例如,对于每一个FLOPs。这种操作无法充分利用现代GPU的大规模计算能力,并会受到明显更低的内存带宽的限制。幸运的是,通过以下观察可以解决这个问题:对第
final rounding decisions仅受到对该列执行的更新的影响,因此对later columns的更新与第"lazily batch" updates从而实现更好的GPU利用率。具体而言,我们同时对block中(参见Figure 2)。仅当一个block被完全处理后,我们才使用下面给出的multi-weight版本的公式,对整个尽管这种策略理论上不减少计算量,但它有效地解决了内存吞吐量瓶颈,在非常大的模型上实际提供了一个数量级的加速,使其成为我们算法的关键组成部分。
即,每次更新一个
batch的权重,而不是单个权重。Cholesky Reformulation:我们必须解决的最后一个技术问题是数值不准确,它可能在现有模型规模下成为主要问题,特别是结合上一步中讨论的block updates。具体来说,可能出现remaining weights的方向,从而导致对应层的arbitrarily-bad quantization。在实践中,我们观察到发生这种情况的概率随模型大小增加:具体来说,对于大于数十亿参数的模型,它几乎肯定对至少一些层发生。主要问题似乎是重复应用公式additional matrix inversion。对于较小的模型,应用阻尼,即将
1%)看起来足以避免数值问题。然而,更大的模型需要更稳健的和更通用的方法。为此,我们首先注意到,从
weight q时的unquantized weights集合),或者更准确地说,从对角线开始的该行中的元素。其结果是,我们可以使用更数值稳定的方法预先计算所有这些行,而不会显著增加内存消耗。实际上,对于我们的对称矩阵Cholesky分解,只是后者存在细微的差别:将行SOTA的Cholesky kernels从Cholesky kernel还可以进一步加速。接下来,我们详细说明Cholesky版本算法所需的所有小改动。虽然大型模型的参数规模可以达到千亿级,但是这里的
layer的inputCholesky分解。完整算法:最后,我们在
Algorithm 1中给出GPTQ的完整伪代码,包括上面讨论的优化。注意:
GPTQ需要依赖输入数据C4数据集中随机采样的128个random 2048 token segments组成的GPTQ有影响?采用比128更多的样本更好,还是更少的样本更好?论文都没有进行消融研究。(在SparseGPT的论文中,作者对calibration数据进行了消融分析,发现::随着calibration样本数量的增加,准确性得到改善。但是当数量超过某个点时,困惑度曲线逐渐变平缓。)注意:
GPTQ仅关注权重activation注意:在当前
layer量化完之后,再将quantized layer从而作为next layer的输入。注意:算法的迭代没有采用随机梯度下降,而是直接用的解析解,因此迭代效率非常高。
注意:
blocksize
6.3 实验
我们首先在小型模型上验证
GPTQ相对于其他accurate-but-expensive quantizers的准确率,这些方法在这些小型模型上可以提供合理的运行时间。接下来,我们检查GPTQ在超大型模型上的runtime scaling。然后,我们通过困难的语言生成任务上的困惑度表现,展示BLOOM和OPT模型族的整体3-bit和4-bit的量化结果。此外,我们展示,当粒度减小到small blocks of consecutive weights时,我们的方法在2-bit量化也很稳定。为补充这一困惑度分析,我们还在一系列标准的
zero-shot任务上评估得到的quantized models。最后,我们关注两个最大(和有趣)的开源可用模型,即Bloom-176B和OPT-175B,在这里我们对几个任务进行详细评估。对于这些模型,我们还提出实际改进,即,为生成式任务减少推理所需的GPU数量、以及端到端加速。设置:我们在
PyTorch中实现了GPTQ,并使用HuggingFace的BLOOM和OPT模型家族。我们使用单个NVIDIA A100 GPU(80GB内存)来量化所有模型(包括175B参数变体)。我们整个GPTQ校准数据(calibration data)由C4数据集中随机采样的128个random 2048 token segments组成。我们强调这意味着GPTQ没有看到任何特定任务的数据,因此我们的结果实际上保持"zero-shot"。我们在min-max grid上执行standard uniform per-row asymmetric quantization,与《LLM.int8(): 8-bit matrix multiplication for transformers at scale》类似。附录A.2.1中提供了更多评估细节。为确保整个压缩过程可以在比运行
full precision model所需的GPU内存显著更小的内存中执行,必须谨慎操作。具体来说,我们一次将一个由6 layers组成的Transformer block加载到GPU内存中,然后累积layer-Hessians并执行量化。最后,通过再次将current block inputs馈入fully quantized block,从而产生next block的new inputs从而进行量化。因此,量化过程不是在full precision model的layer inputs上运行,而是在已经部分quantized model的actual layer inputs上运行。我们发现,这在几乎没有额外成本的情况下带来显着改进。baselines:我们的主要基准线,记做
RTN,将所有权重舍入到与GPTQ使用的完全相同的asymmetric per-row grid上的nearest quantized value;这对应于SOTA的LLM.int8()的weight quantization。这目前是非常大规模语言模型的量化中所有工作的选择方法:它的运行时间随着具有数十亿参数的网络很好地扩展,因为它只执行直接舍入(direct rounding)。正如我们稍后将更深入讨论的,像
AdaRound(《Up or down? Adaptive rounding for post-training quantization》)或BRECQ(《BRECQ: Pushing the limit of post-training quantization by block reconstruction》)这样更精确的方法目前对于数十亿参数的模型来说计算开销太大,这也是本文的主要关注点。尽管如此,我们还展示
GPTQ在小型模型上与这些方法相媲美,同时也可扩展到OPT-175B这样的巨型模型。
Quantizing Small Models:作为第一个消融研究,我们在ResNet18和ResNet50上比较GPTQ与SOTA的post-training quantization: PTQ方法的性能,这些是标准的PTQ benchmarks,设置与《Optimal Brain Compression: A framework for accurate post-training quantization and pruning》相同。结果如
Table 1所示。可以看到:在
4-bit时,GPTQ的表现与最accurate的方法相当。在
3-bit时GPTQ与最accurate的方法相比略差一些。与此同时,
GPTQ明显优于AdaQuant,后者是先前PTQ方法中最快的。
此外,我们还与两个小型语言模型
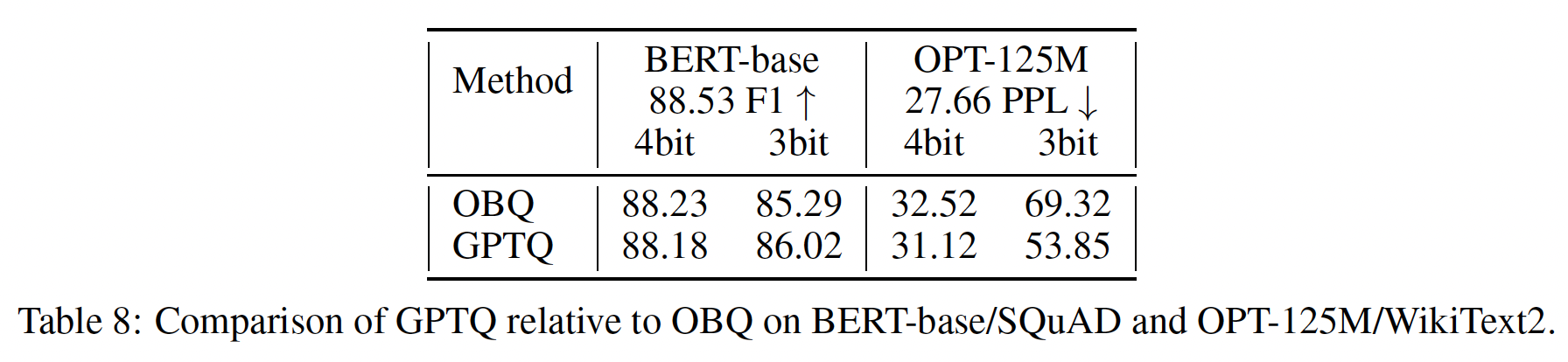
BERT-base和OPT-125M上的full greedy OBQ方法进行了比较。结果如附录Table 8所示。可以看到:在4-bit时,两种方法的性能相似;在3-bit时,出人意料的是,GPTQ的表现略好一些。我们怀疑这是因为OBQ使用的一些额外启发式方法,如early outlier rounding,可能需要仔细调整从而在non-vision模型上获得最佳性能。总体而言,
GPTQ似乎与小型模型的SOTA的PTQ方法相媲美,而只需要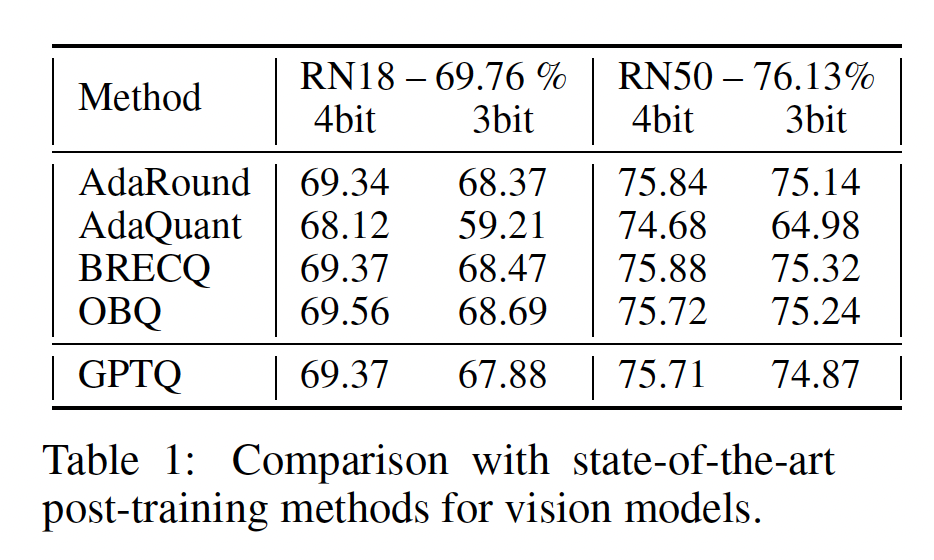
Runtime:接下来,我们通过GPTQ测量full model quantization time(在单个NVIDIA A100 GPU上);结果如Table 2所示。可以看出:GPTQ可以在几分钟内量化1B-3B参数的模型,在几小时内量化175B参数的模型。作为参考,基于
straight-through的方法ZeroQuant-LKD(《ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers》)报告了一个1.3B参数模型的3小时runtime(在相同硬件上),这会线性外推到175B参数模型的数百小时(几周)。adaptive rounding-based的方法通常采用大量SGD steps,因此计算代价甚至更高(《Up or down? Adaptive rounding for post-training quantization》、《BRECQ: Pushing the limit of post-training quantization by block reconstruction》)。

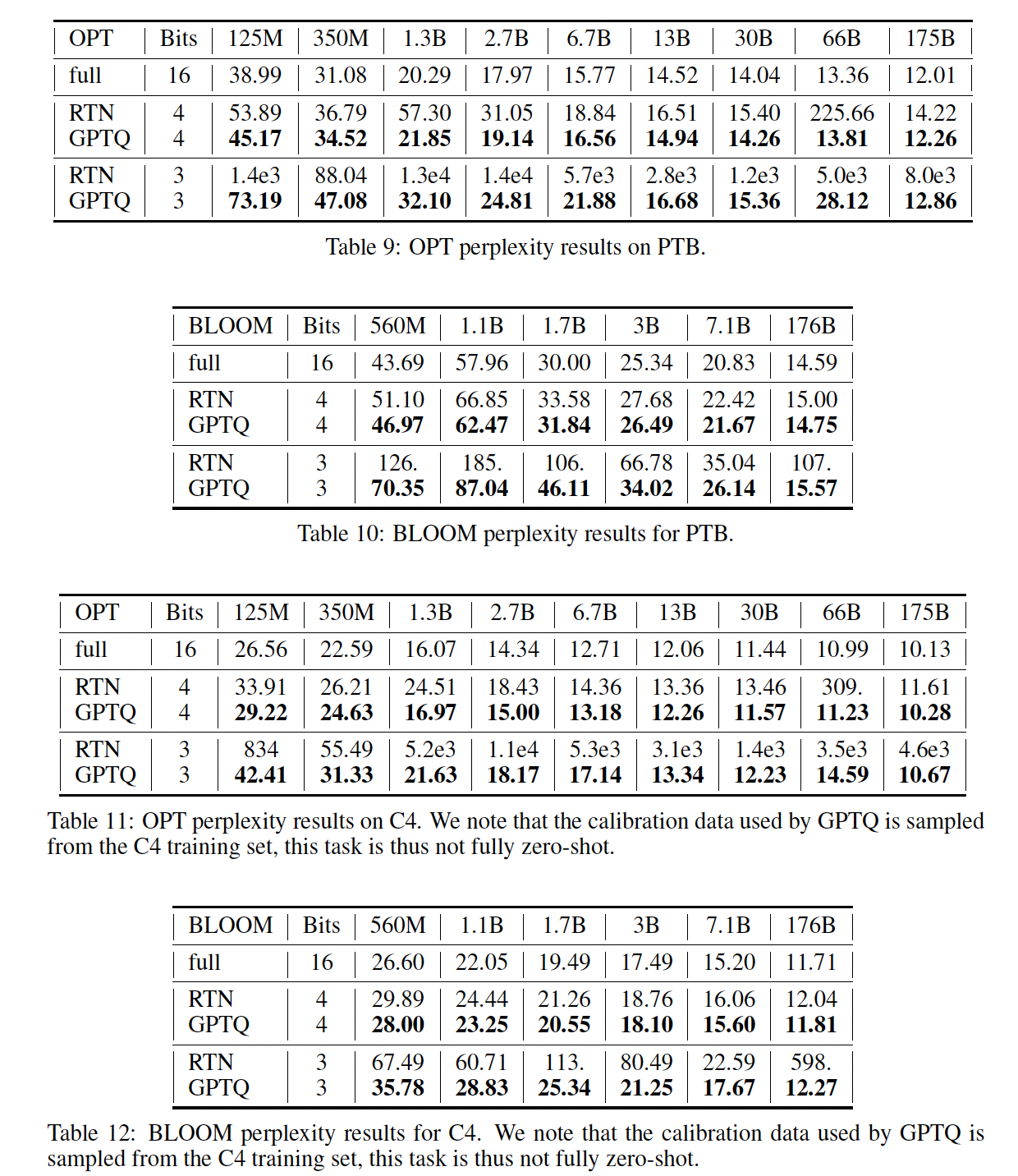
Language Generation:我们通过压缩整个OPT和BLOOM模型系列到3-bit和4-bit开始large-scale研究。然后我们在几项语言任务上评估这些模型,包括WikiText2(参考Figure 1和Table 4)、Penn Treebank: PTB、和C4(都在附录A.3中)。我们关注这些基于困惑度的任务,因为已知它们特别敏感于model quantization(《ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers》)。在
OPT模型上,GPTQ明显优于RTN,差距很大。例如,在175B参数模型的4-bit下,GPTQ只损失了0.03的困惑度,而RTN下降了2.2的困惑度(甚至比规模小10倍的full-precision 13B model表现还差)。在
3比特下,RTN完全崩溃,而GPTQ仍能维持合理的困惑度,特别是对较大的模型。BLOOM显示了类似的模式:方法之间的差距通常稍小一些,这表明这个模型系列可能更容易被量化。一个有趣的趋势(参见
Figure 1)是:除OPT-66B之外,较大的模型似乎通常更容易被量化。这对实际应用来说是个好消息,因为这些也是最需要压缩的情况。


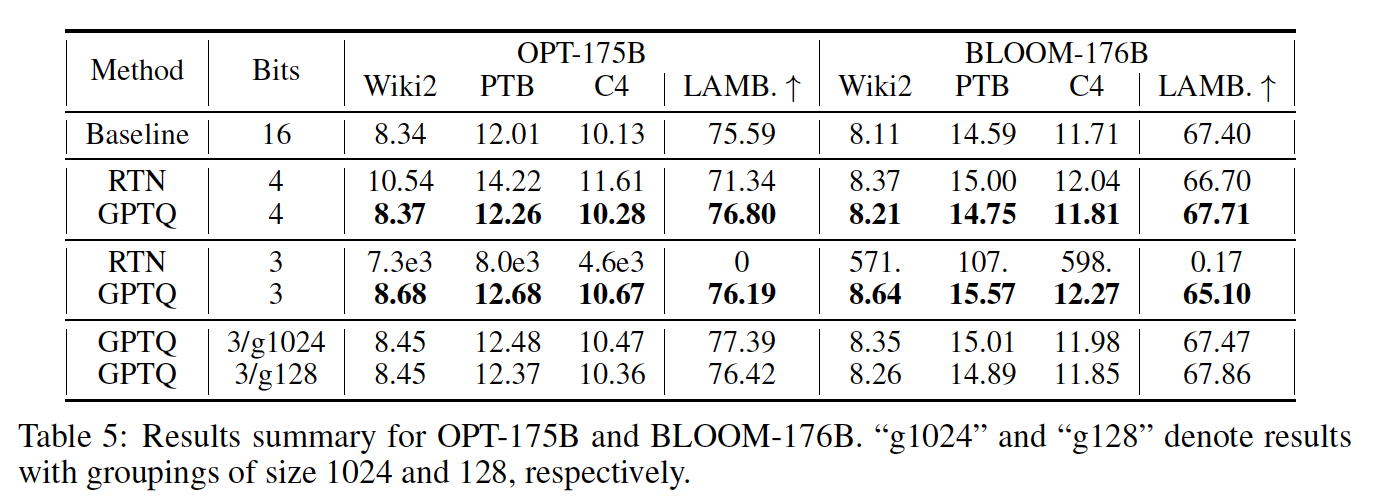
175 Billion Parameter Models:现在我们检查BLOOM-176B和OPT-175B,这是最大的公开可用的稠密模型。Table 5总结了它们在Wikitext-2、PTB、C4上的结果。我们观察到:在
4-bit下,GPTQ模型的困惑度仅比full-precision versions低OPT-175B上以较大优势超越了RTN的结果。在
3-bit下,RTN崩溃,而GPTQ仍能在大多数任务上维持良好的性能,在超过5倍压缩的情况下仅仅损失0.3-0.6点。我们注意到,通过更细粒度的分组(
《nuQmm: Quantized matmul for efficient inference of large-scale generative language models》),GPTQ的准确率可以进一步提高:group-size =1024(约0.02 extra bits)改善了平均困惑度约0.2;group-size =128(约0.15 extra bits)继续改善了平均困惑度约0.1,与未压缩的困惑度只差0.1-0.3。我们注意到,
grouping与GPTQ互相协作得非常好,因为可以在每一层的量化过程期间确定group parameters,总是使用most current updated weights。
实际加速:最后,我们研究实际应用。作为一个有趣的
case,我们关注OPT-175B模型:量化到3-bit后,这个模型占用约63GB内存,包括embedding layer和output layer(它们保持full FP16 precision)。另外,为所有层存储keys和values的完整历史,这是generation任务的常见优化,对于最大2048 tokens又占用约额外9GB。因此,我们实际上可以将整个quantized model装入单个80GB A100 GPU中,可以通过在推理期间需要时动态地dequantizing layers来执行(使用4-bit模型将不会完全适合单个GPU内存)。作为参考,标准FP16执行需要5个80GB GPU;而SOTA的8-bit LLM.int8() quantizer需要3个这样的GPU。接下来,我们考虑
language generation,这是这些模型最吸引人的应用之一,目标是减少延迟。与LLM.int8()不同,其中LLM.int8()减少了内存成本但与FP16 baseline的runtime相同,我们展示了我们的quantized models可以实现显着的加速。对于language generation,模型一次处理和输出一个token,对于OPT-175B,每个token需要几百毫秒。提高生成结果的速度具有挑战性,因为计算主要由matrix-vector乘法所主导。与matrix-matrix乘法不同,matrix-vector乘法主要受内存带宽限制。我们通过开发quantized-matrix full-precision-vector product kernel来解决这个问题,该kernel通过在需要时动态地dequantizing weights来执行matrix-vector乘法。最重要的是,这不需要任何activation quantization。虽然dequantization消耗了额外计算,但kernel需要访问更少内存,如Table 6所示,这导致显着加速。我们注意到,几乎所有加速都归因于我们的kernels,因为在我们的标准HuggingFace-accelerate-like setting中,通信成本可忽略不计(详见附录A.2.2)。例如:
使用我们的
kernels,通过GPTQ获得的3-bit OPT-175B模型在单A100 GPU上运行时,与FP16版本(在5个GPU上运行)相比,average time per token快约3.25倍。对于
NVIDIA A6000(具有更低的内存带宽),这种策略甚至更有效:在2个A6000 GPU上执行3-bit OPT-175B模型将延迟从FP16版本的589毫秒(在8个GPU上)降低到130毫秒,延迟降低了4.5倍。

Zero-Shot Tasks:虽然我们的重点是language generation,但我们还在一些流行的zero-shot任务上评估了quantized models的性能,即LAMBADA、ARC (Easy and Challenge)、和PIQA。Figure 3可视化了模型在LAMBADA上的性能(参见Table 5中的"Lamb."结果)。我们观察到之前类似的行为,但是一些异常情况是:1):在4-bit,量化对所有模型来说似乎 “更容易”, 即使RTN也表现相对良好。2):在3-bit,RTN崩溃 而GPTQ仍然提供良好的准确率。
我们在附录
A.4中提供了更多结果。
Additional Tricks:虽然到目前为止我们的实验仅集中在普通的row-wise quantization上,但我们想强调GPTQ与基本上任何quantization grid choice兼容。例如,它很容易与standard grouping(《QSGD: Randomized quantization for communication-efficient stochastic gradient descent》、《nuQmm: Quantized matmul for efficient inference of large-scale generative language models》)相结合,即对groups of g consecutive weights应用独立的量化。如Table 5最后几行所示,这在3-bit对最大模型可以带来显着的额外准确率提升。此外,如Figurer 4所示,它显着减少了中等大小模型在4-bit precision下的准确率损失。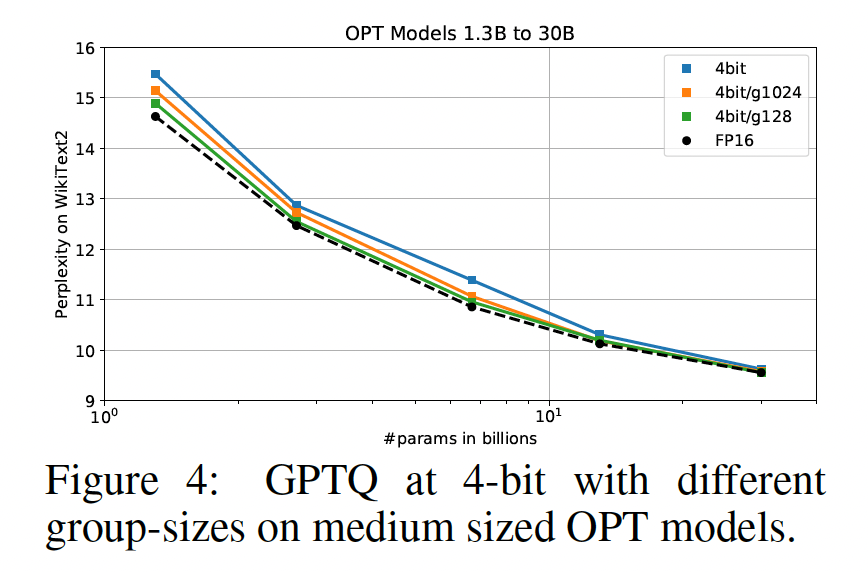
极端量化:最后,
grouping也使得在平均2-bit per parameter的极端量化上获得合理性能成为可能。Table 7显示了在不同group-size下将最大模型量化为2-bit时在WikiText2上的结果。在大约
2.2 bit(group-size 128; using FP16 scale and 2-bit zero point per group)时,困惑度的增加还不到1.5。而在约
2.6 bit(group-size 32)时,困惑度增加到0.6-0.7,这只比普通的3-bit略差,并且对实际kernel implementations可能很有趣。此外,如果我们将
group-size减小到8,我们可以应用三值(ternary)量化(-1, 0, +1),在OPT-175B上获得9.20的困惑度,增加不到1个点。虽然与上述2-bit数字相比,这在平均上导致较差的压缩,但这种模式可以在FPGA等定制硬件上有效实现。
总之,这些结果是首次向着极端压缩非常大型语言模型的有希望的第一步,甚至低于平均
3-bit per parameter。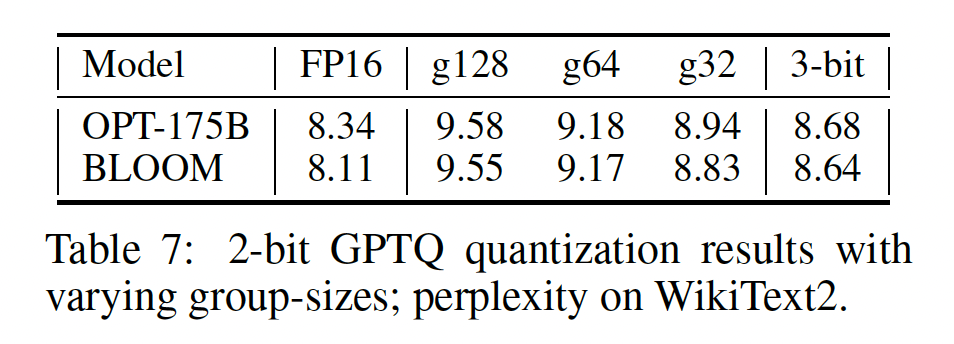
6.4 讨论
局限性:我们强调一些重要的局限性:
在技术上,我们的方法来自减少内存移动带来的加速,而没有导致计算减少。
注意,这是因为
GPU kernels目前还不支持3-bit整数和FP 16的乘法,因此在推理过程中,3-bit整数被逆量化为FP16,然后进行FP16和FP16的乘法运算,这就是作者开发的quantized-matrix full-precision-vector product kernel。此外,我们的研究侧重于生成式任务,而且不考虑
activation quantization。
这些是自然的未来工作方向,我们相信这可以通过精心设计的
GPU kernels和现有技术来实现(《ZeroQuant: Efficient and affordable post-training quantization for large-scale transformers》、《Extreme compression forpre-trained transformers made simple and efficient 》)。