四十三、Scaling Laws for Neural Language Models[2020]
language为人工智能的研究提供了一个天然的领域,因为绝大多数的reasoning task都可以用语言有效地表达和评估,而且世界上的文本通过generative modeling为无监督学习提供了大量的数据。最近,深度学习在language modeling方面取得了快速进展,SOTA模型在许多特定任务上的表现接近人类水平。人们可能预期语言建模的性能取决于模型结构、神经模型的规模、用于训练模型的算力、以及用于训练模型的数据。在论文
《Scaling Laws for Neural Language Models》中,作者将实证研究language modeling loss对所有这些因素的依赖性,重点是Transformer架构。通过在语言任务上的性能的上限和下限,使作者能够研究scale中超过七个数量级的趋势。在整个过程中,作者将观察到性能的精确的
power-law scaling,其中性能作为训练时间、上下文长度、数据集大小、模型大小、compute budget的函数。相关工作:
幂律(
power-law)可以从各种来源产生。在密度估计(density estimation) 模型和随机森林模型中,随模型规模和数据集大小有关的power-law scaling可能与我们的结果有关。这些模型表明,幂律指数可能有一个非常粗糙的解释,即数据中相关特征数量的倒数。最近的工作
《Deep learning scaling is predictable,empirically》、《Beyond human-level accuracy: Computational challenges in deep learning》也研究了模型大小和数据大小之间的scaling;他们的工作可能是文献中最接近我们的工作。然而,请注意,《Deep learning scaling is predictable,empirically》发现数据集大小与模型大小的超线性scaling,而我们发现的是亚线性scaling。我们关于计算量的
optimal allocation的发现和《One epoch is all you need》之间有一些相似之处,包括power-law learning curve。EfficientNet似乎也服从于准确率和模型大小之间的近似的幂律关系。最近的工作
《A constructive prediction of the generalization error across scales》研究了各种数据集的数据集大小和模型大小的scaling,并符合与我们类似的分析方法。
EfficientNet主张以指数方式scale模型的深度和宽度,以获得图像模型的最佳性能,导致宽度作为深度的函数出现power-law scaling。我们发现,对于语言模型来说,这个幂律在scaling up时应该是大致为1(即,width/depth的比例应该保持固定)。但更重要的是,我们发现,与语言模型的overall scale相比,精确的架构超参数并不重要。在
《Residual networks behave like ensembles of relatively shallow networks》中,有人认为deep的模型可以作为较浅的模型的ensemble,这有可能解释这一发现。早期的工作
《Wide residual networks》比较了宽度和深度,发现wide ResNet在图像分类上可以胜过deep ResNet。一些研究固定了每个数据样本的计算量(计算量往往与模型参数的数量成正比,固定这个值意味着固定模型大小),而我们研究的是与模型大小和
training computation的scaling。
许多研究(
《High-dimensional dynamics of generalization error inneural networks》、《Reconciling modern machine learning and the bias-variance trade-off》对高度过参数化的模型(highly overparameterized model)的泛化进行了研究,发现当模型规模达到数据集规模时,会出现"jamming transition"(《Scaling description of generalization with number of parameters in deep learning》)(这可能需要超出典型实践许多数量级的training,尤其是不使用早停)。我们没有观察到这样的transition,并发现所需的训练数据在模型大小上呈亚线性scaling。模型规模的扩展,特别是在large width上的扩展,可能为思考我们的一些scaling关系提供了一个有用的框架。我们关于
optimization的结果(如学习曲线的形状),很可能可以用一个noisy的二次模型来解释,它可以在现实环境中提供相当准确的预测(《Which algorithmic choices matter at which batch sizes? insights from a noisy quadratic model》)。定量评估这种联系将需要海森谱(Hessian spectrum) 的特性。
这篇论文直接看结论部分即可,剩余的大多数都是实验报告。
43.1 背景和模型
符号:
token的交叉熵损失的平均值,但在某些情况下,我们会报告上下文中特定位置处的token的损失。vocabulary embedding和positional embedding。non-embedding的training总计算量的估计,其中batch size,training steps数量(即parameter updates)。我们引入PF-days为单位,其中一个PF-days表示token。critical batch size,在后续内容中定义和讨论。使用critical batch size的训练提供了训练时间和计算效率之间的大致上的最佳trade-off。loss的最小non-embedding compute的估计。这是在模型以远小于critical batch size的batch size进行训练时将使用的training compute。较小的
batch size可以实现较小的计算量、但是需要较大的训练时间。loss所需的最小training steps数的估计。这也是如果模型在batch size远大于critical batch size的情况下所使用的training steps数量。较大的
batch size可以实现较小的训练时间、但是需要较大的计算量。loss缩放的幂率函数的指数,其中
注,这里的
loss函数是test loss,而不是train loss。我们在
WebText2上训练语言模型,这是WebText数据集的扩展版本,使用byte-pair encoding: BPE进行tokenize,vocabulary size为autoregressive log-likelihood(即交叉熵损失),在1024-token的上下文中取平均,这也是我们的主要性能指标。我们在WebText2测试集、以及其它一些测试集上记录loss。我们主要训练decoder-only Transformer模型,尽管我们也训练LSTM模型和Universal Transformer以进行比较。模型的性能评估指标是测试集上的交叉熵损失。
a. Transformer 的参数 scaling 和计算量 scaling
我们使用超参数
residual stream的维度)、feed-forward layer的维度)、attention output的维度)和attention head的数量)对Transformer架构进行参数化。我们在输入上下文中包括token,除另有说明外否则默认采用我们用
non-embedding parameters的数量(推导过程参考Table 1):其中,我们排除了
bias项和其他次要的项。我们的模型在embedding矩阵中也有positional embedding,但我们在讨论 "模型大小"scaling law。评估
Transformer的前向传播大致上包括add-multiply operation),其中系数2来自于矩阵乘法中使用的multiply-accumulate operation。下表中包含了更详细的每个操作的参数数量和计算次数。
对于
token的context-dependent的计算成本是总计算量的一个相对较小的部分。由于我们主要研究training compute的估计中不包括context-dependent项。考虑到反向传播(大约是前向传播计算量的两倍),我们为每个training token将估计的non-embedding compute定义对于
GPT-3 175B,
b. 训练过程
除非另有说明,我们用
Adam优化器训练模型,其中训练了固定的batch size为512个序列,每个序列包含1024 tokens。由于内存限制,我们最大的模型(超过
1B个参数)是用Adafactor训练的。我们试验了各种学习率和
schedules。我们发现,收敛的结果在很大程度上与learning rate schedule无关。除非另有说明,我们的数据中包括的所有training runs都使用了同一个learning rate schedule,即:3000步的线性预热,然后是余弦衰减学习率到零。
我们用各种学习率和
schedule进行了实验。下图显示了一个小型语言模型的一系列schedules和测试结果。我们的结论是,只要total summed learning rate足够大,而且schedule包括一个预热期、以及最后衰减到接近零的学习率,那么learning rate schedule的选择基本上是不重要的。schedules之间的方差似乎是统计学上的噪音,并为不同training runs之间的方差的scale提供一个粗略的衡量标准。在较大的模型上的实验表明,对于不同的模型大小,不同的随机种子之间的final test loss的方差的幅度是大致不变的。我们发现,较大的模型需要一个较小的学习率来防止发散,而较小的模型可以容忍较大的学习率。为了实现这一点,在大多数
runs中使用了以下经验法则:我们期望这个公式可以被改进。
可能存在对
network width的依赖性,可能是由initialization scale设定的。对于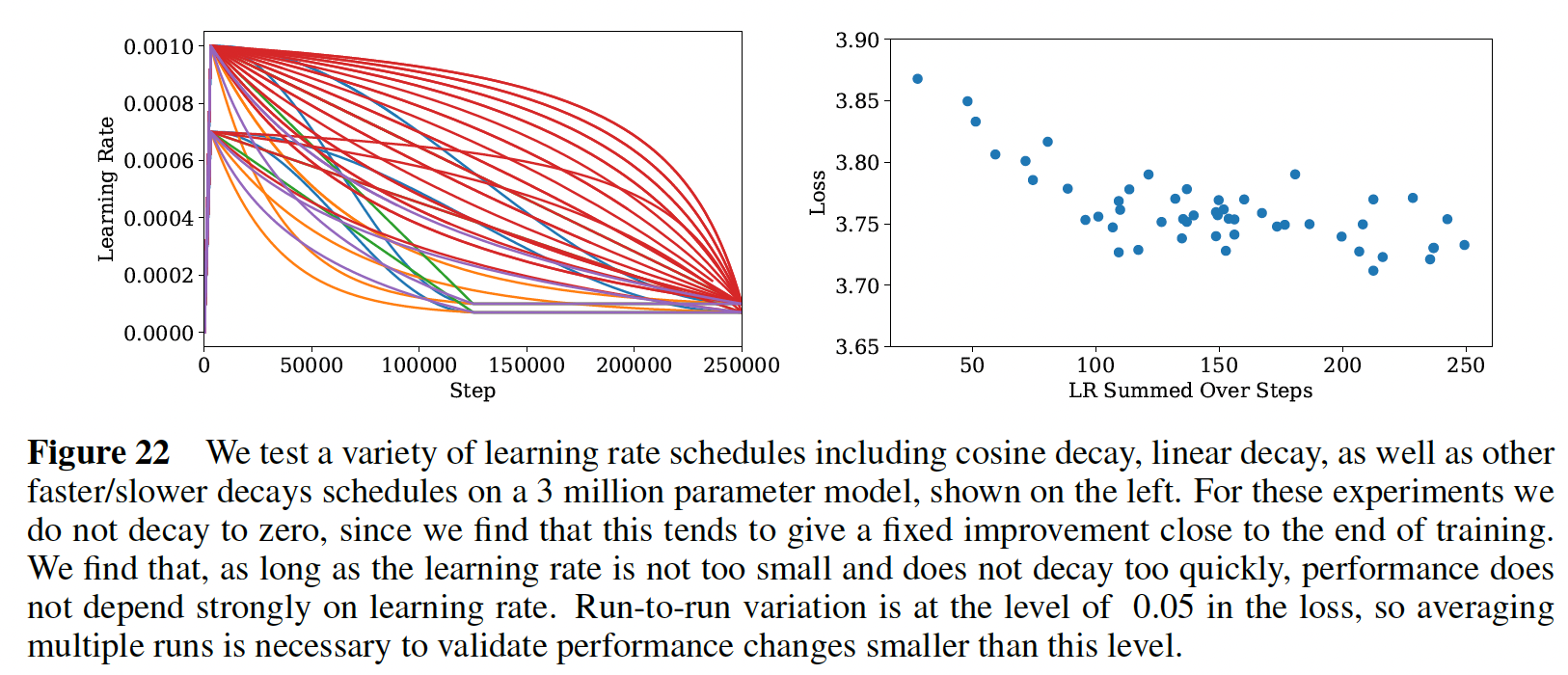
c. 数据集
我们在
GPT2中描述的WebText数据集的扩展版本上训练我们的模型。最初的WebText数据集是对Reddit在2017年12月的外链(包含Reddit用户的至少三个点赞)的网络爬取。在第二个版本中(即,WebText2),我们增加了2018年1月至10月期间的Reddit外链,也是至少有3个点赞的。karma阈值(即,点赞的数量阈值)作为一种启发式方法,用于判断人们是否认为该链接有趣或有用。新链接的文本是用Newspaper3k python library提取的。总的来说,该数据集由
20.3M篇文档组成,包含96GB的文本和GPT2中描述的可逆的tokenizer,产生token。我们保留了其中的token作为测试集,并且我们还在类似的Books Corpus、Common Crawl、English Wikipedia、以及公开的Internet Books集合中进行测试。
43.2 实验结果和 Basic Power Laws
为了刻画
language model scaling,我们训练了各种各样的模型,其中改变了一些因子,包括:模型大小:从
768到1.5B个non-embedding参数。数据集大小:从
22M到230B个token。模型
shape:包括depth、width、attention head、以及feed-forward dimension。上下文长度:大多数
runs设置为1024,但我们也尝试使用较短的上下文。batch size: 大多数runs设置为batch size从而测量critical batch size。
43.2.1 Transformer Shape
当我们固定
non-embedding参数总数Transformer的性能对shape参数为了确定这些结果,我们用固定的模型大小来训练模型,同时改变一个超参数。
这对于
head的维度,使得右图中,每条曲线对应于固定的
当改变
中间图中,每条曲线对应于固定的参数量同时改变
同样地,为了在固定的模型大小下改变
Table 1中的参数数量所要求的。左图中,每条曲线对应于固定的参数量同时改变
如果
deeper Transformer有效地表现为shallower model的ensembles,那么就会导致ResNet的建议(《Residual networks behave like ensembles of relatively shallow networks》)。结果显示在下图中。下图中,不同的模型形状,得到的
test loss差异很小,差异基本上都在10%以内。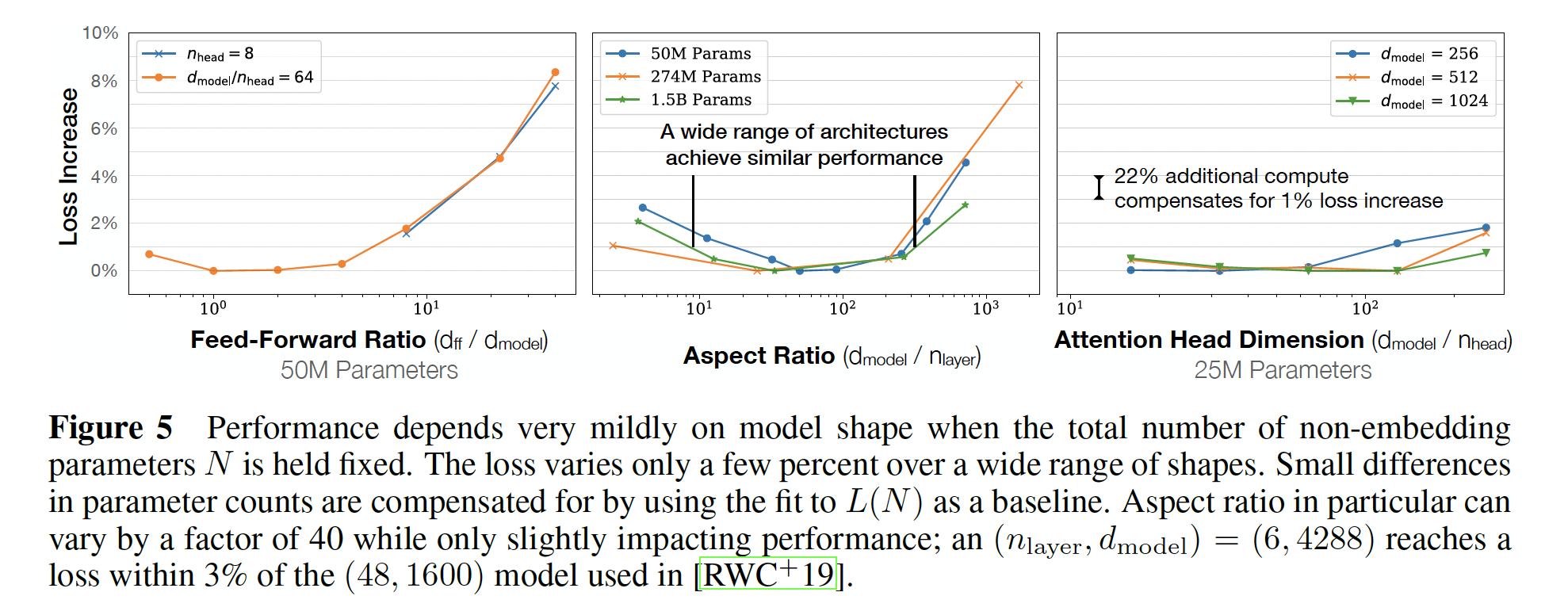
43.2.2 non-embedding 参数数量 N
a. 实验结果
在下图中,我们展示了各种模型的性能,从
shapeshape从WebText2数据集上训练到接近收敛,并且观察到没有过拟合(除了非常大的模型,因为对于非常大的模型则可能过拟合)。如
Figure 1右图所示,我们发现关于non-embedding参数数量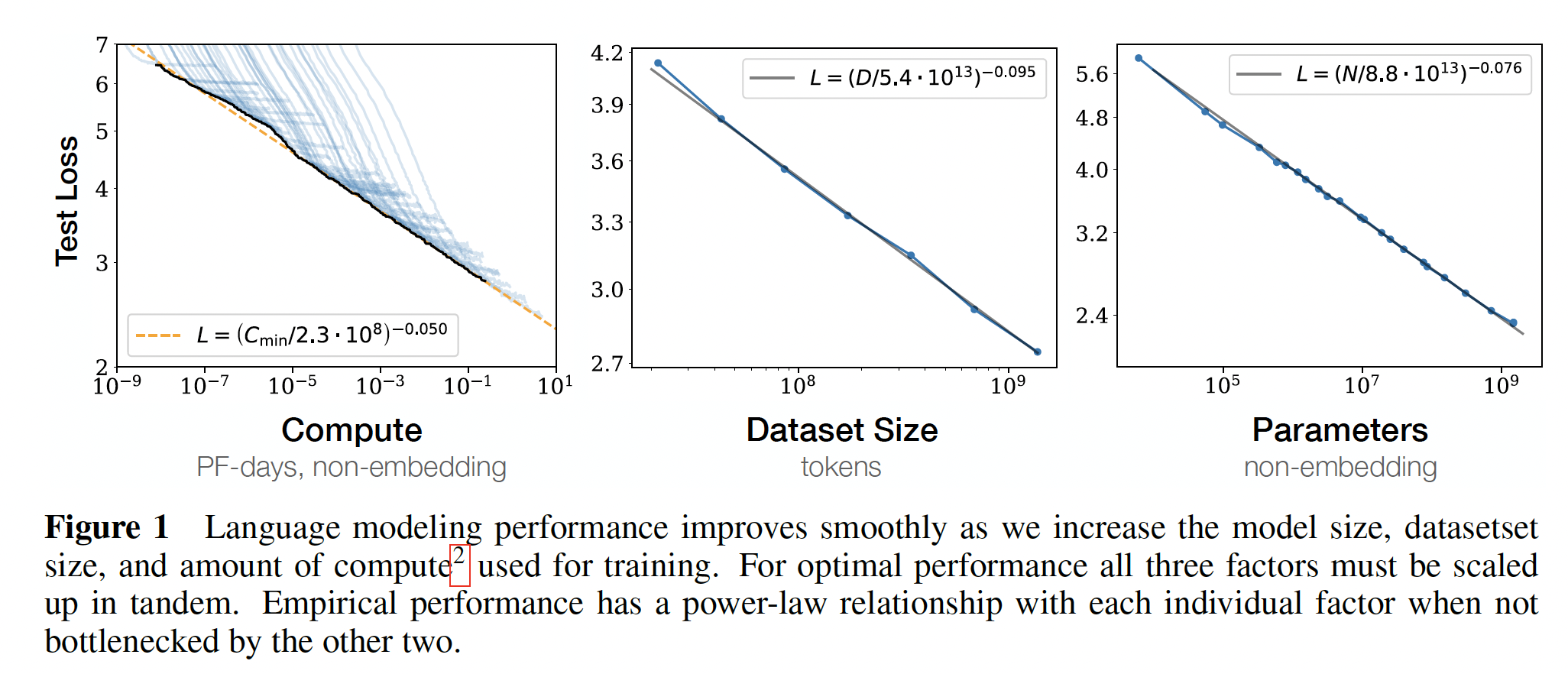
要观察这些趋势,关键是要研究模型性能与
embedding参数),趋势就有些模糊了(如下左图所示)。这表明,embedding matrix可以做得更小而不影响性能,这在最近的工作中已经看到了(《Albert: A lite bert for self-supervised learning of language representations》)。ALBert将embedding matrix分解为两个低维矩阵的乘积,这等价于降低了embedding matrix的大小。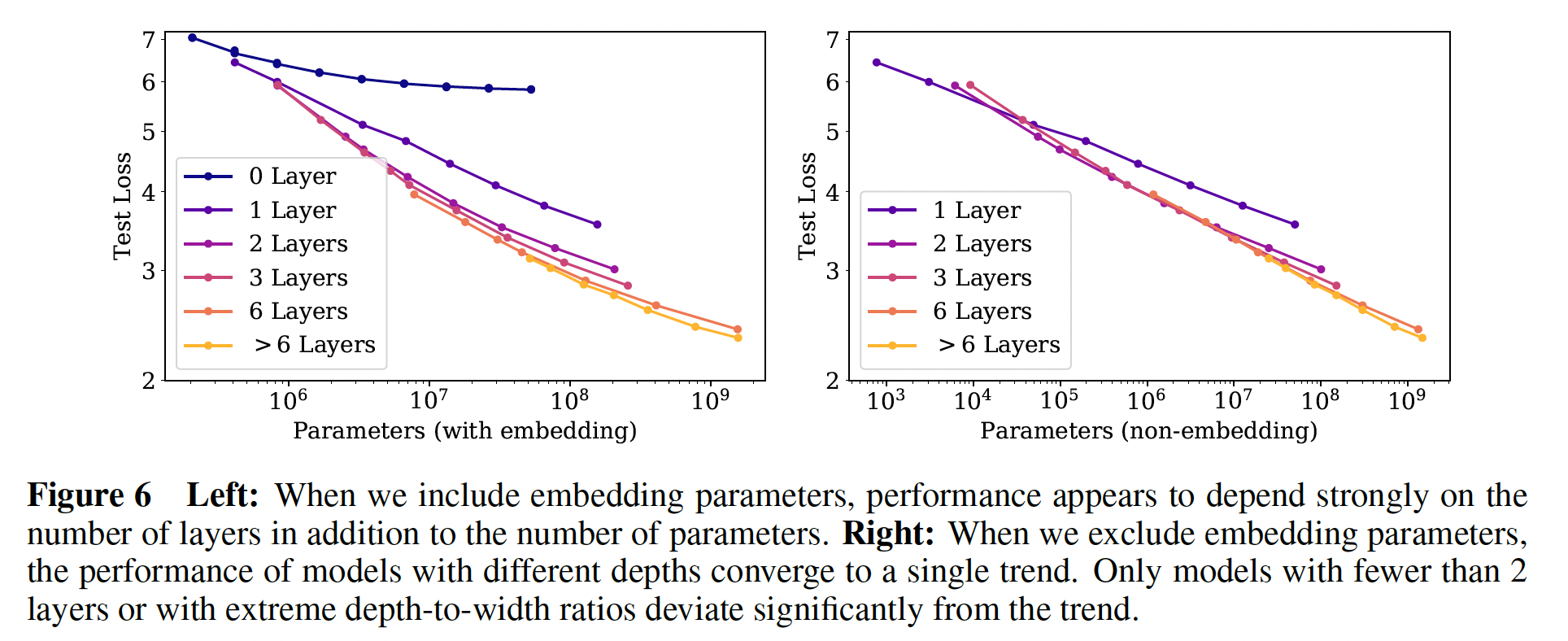
尽管这些模型是在
WebText2数据集上训练的,但它们在其他各种数据集上的test loss也是左图、右图的详细说明参考 “数据分布之间的泛化” 章节。
b. 与 LSTM 和 Universal Transformer的比较
在下图中,我们比较了
LSTM和Transformer的性能与non-embedding参数数量LSTM是用与Transformer相同的数据集和上下文长度来训练的。从右图中我们可以看出,LSTM对于上下文位置中头部出现的token表现得和Transformer一样好,但是对于上下文位置中尾部出现的token则无法与Transformer的表现相媲美。红色曲线为
LSTM,蓝色曲线为Transformer。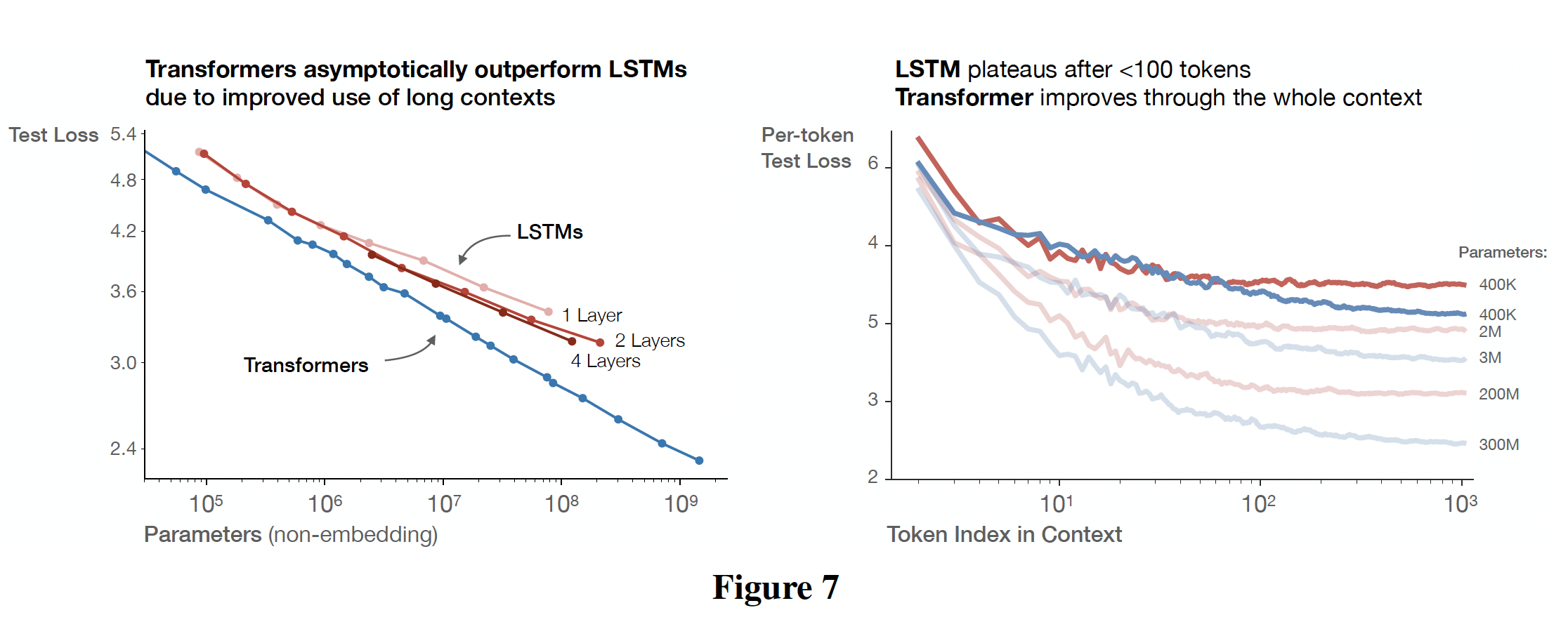
下图中给出了模型性能与上下文位置之间的幂律关系,其中,除了第一个
token之外(最上面的一条曲线),都显示了随着模型大小的增加而稳定地改善,表明快速识别模式的能力有所提高。我们还包括用很小的
token上超越我们最大的因为对于
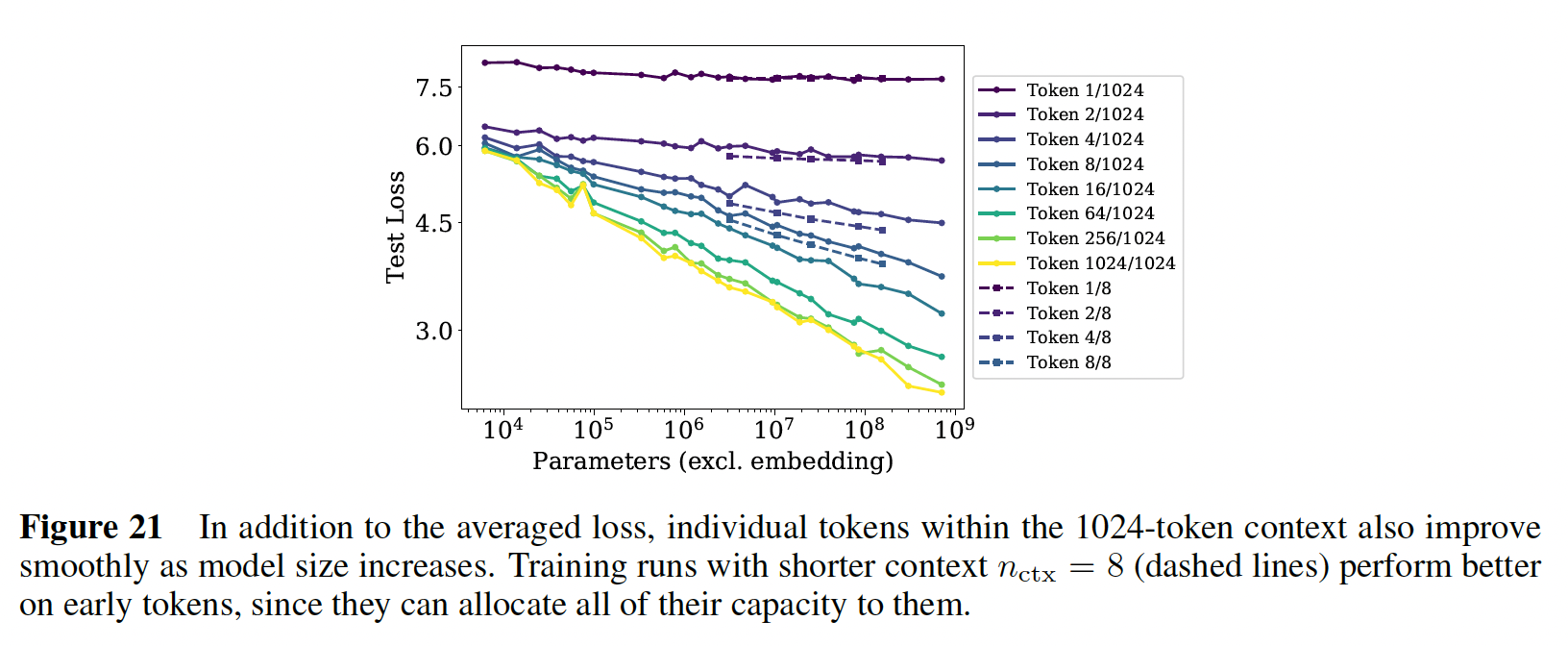
在固定模型大小的情况下,
loss scale似乎与上下文中的位置power-law correlation的结果,或者是模型结构和optimization的一个更普遍的特征。它为在更大的上下文中训练的潜在好处(或潜在不足)提供了一些建议。不仅较大的模型在early tokens时也改善得更快,这表明较大的模型在检测less contextual information的模式时更有效率。在右边的图中,我们显示了对于一个固定的模型,
per-token性能是如何作为training steps的函数而变化的。early tokens在训练过程中更快地被学好,而末尾的tokens在训练的后期才能训练好。左图:每条曲线对应一个模型(不同模型大小)的
per-token test loss,在模型训练结束后。右图:每条曲线对应一个
token index的学习曲线,在模型训练过程中,固定的模型。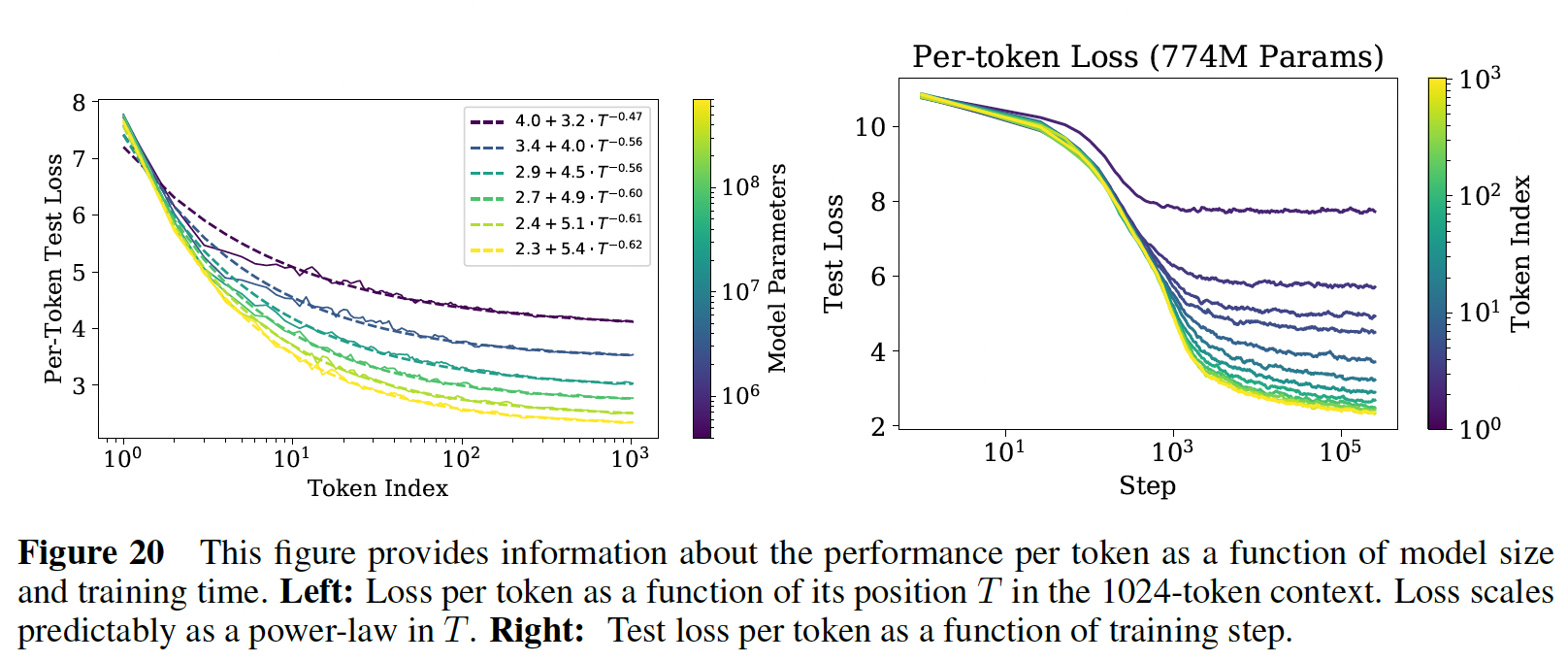
我们还在下图中比较了标准
Transformer和recurrent Transformer(《Universal transformers》)的性能。recurrent Transformer模型复用参数,因此表现得略好(右图),但代价是每个参数的额外计算量。左图把
reuse的参数也认为是全新的,因此参数规模会变大。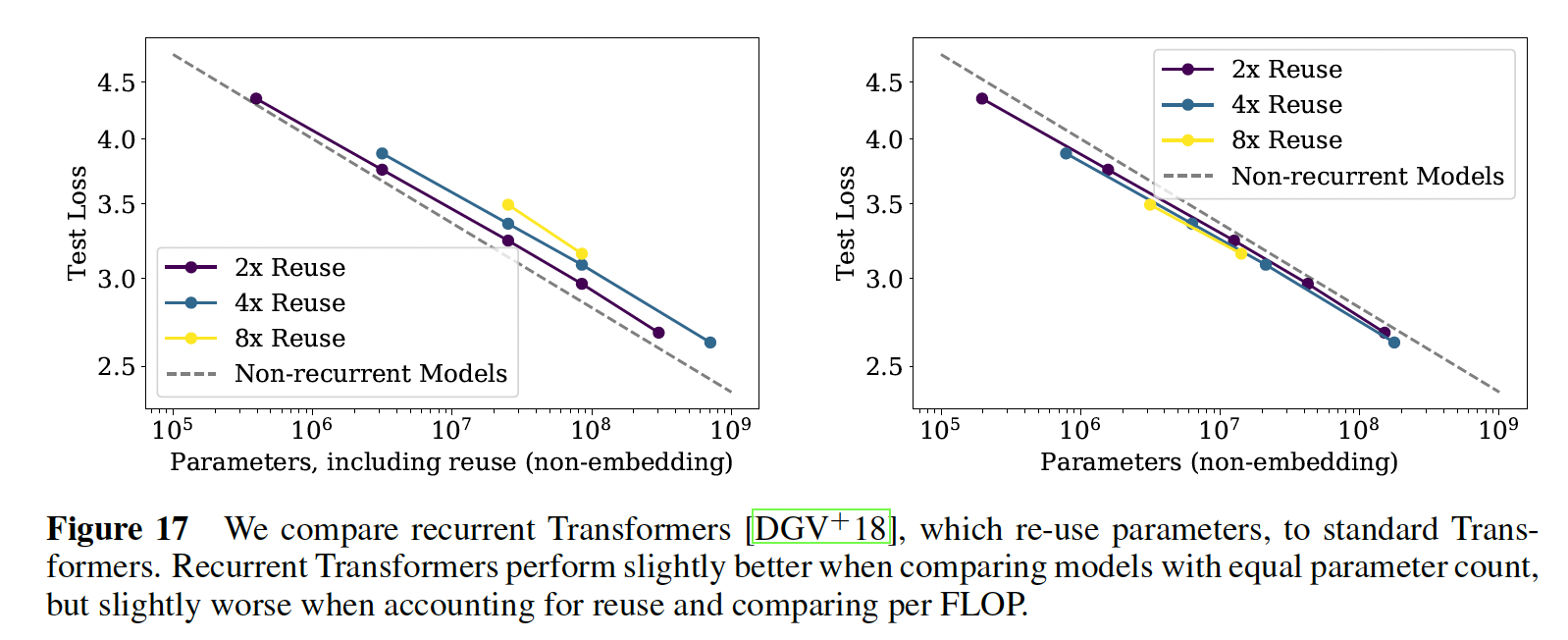
c. 数据分布之间的泛化
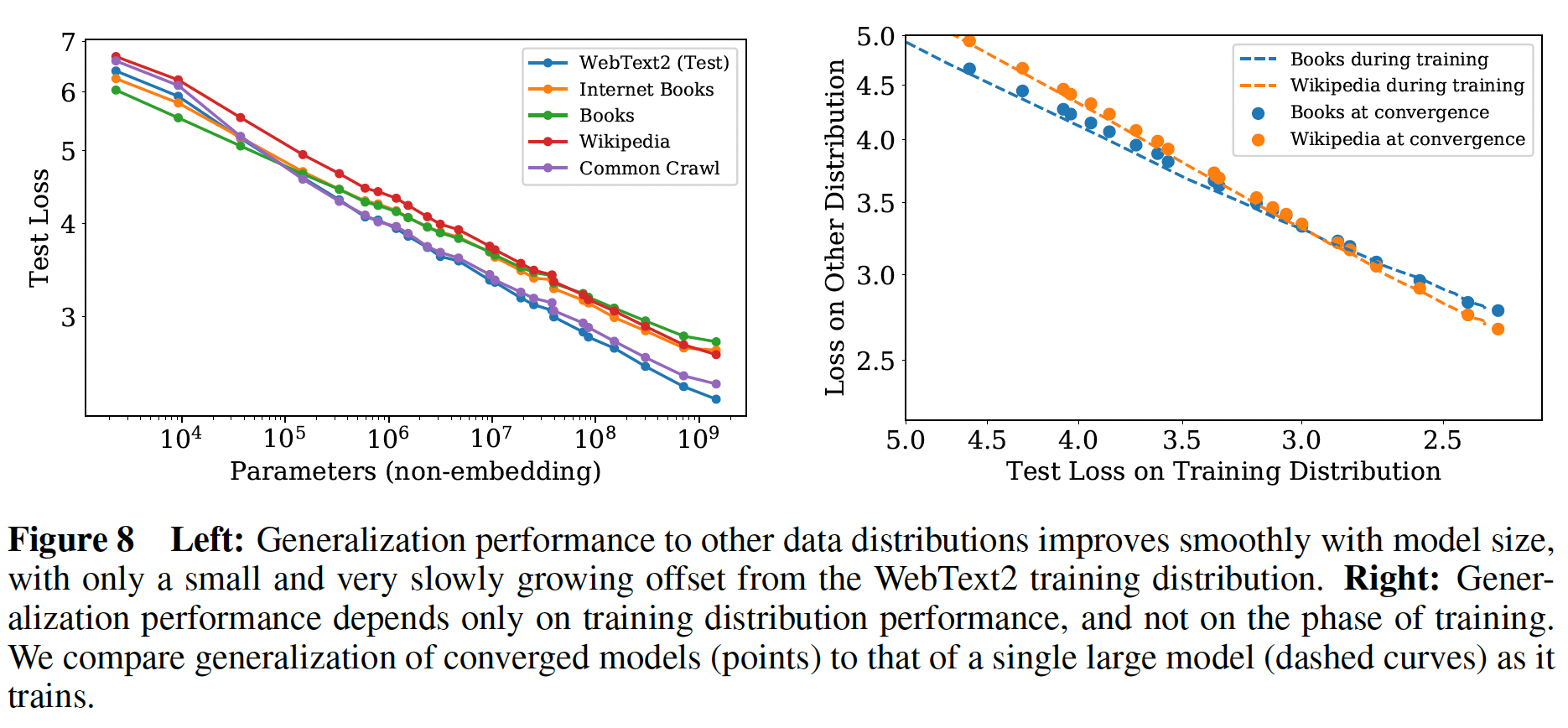
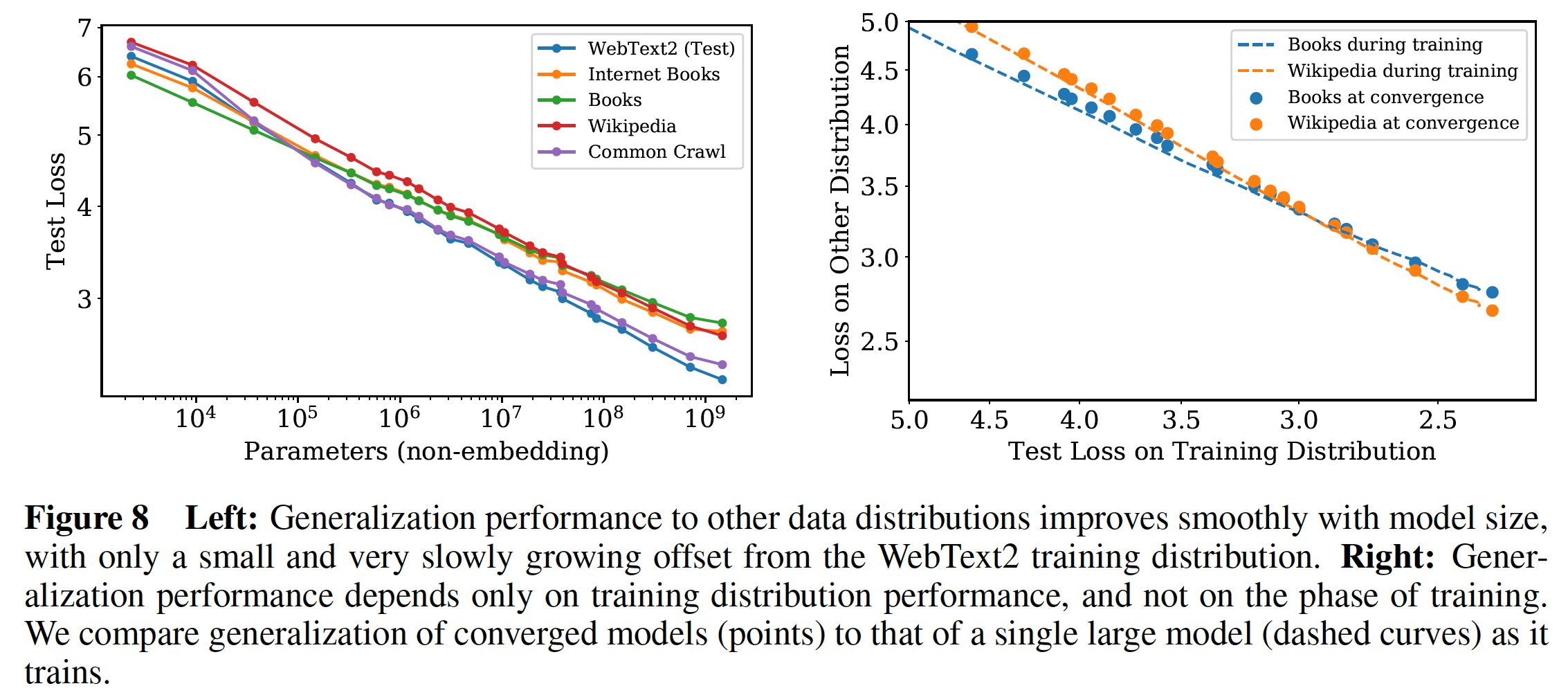
我们还在一组额外的文本数据分布上测试了我们的模型。下图显示了这些数据集上的
test loss与模型大小的关系。在所有情况下,模型都只在WebText2数据集上训练过。从左图中我们看到,在这些其他数据分布上的
loss随着模型规模的增加而平滑地改善,直接地平行于WebText2的test loss曲线。从右图中我们发现,泛化性几乎完全取决于
in-distribution validation loss,而不取决于训练的持续时间、或接近于收敛的程度。虚线表示单个大型模型在它训练过程中,所得到的
test loss;圆点表示很多收敛的模型对应的test loss。
我们还观察到对模型深度没有依赖性(在固定模型大小的条件下)。
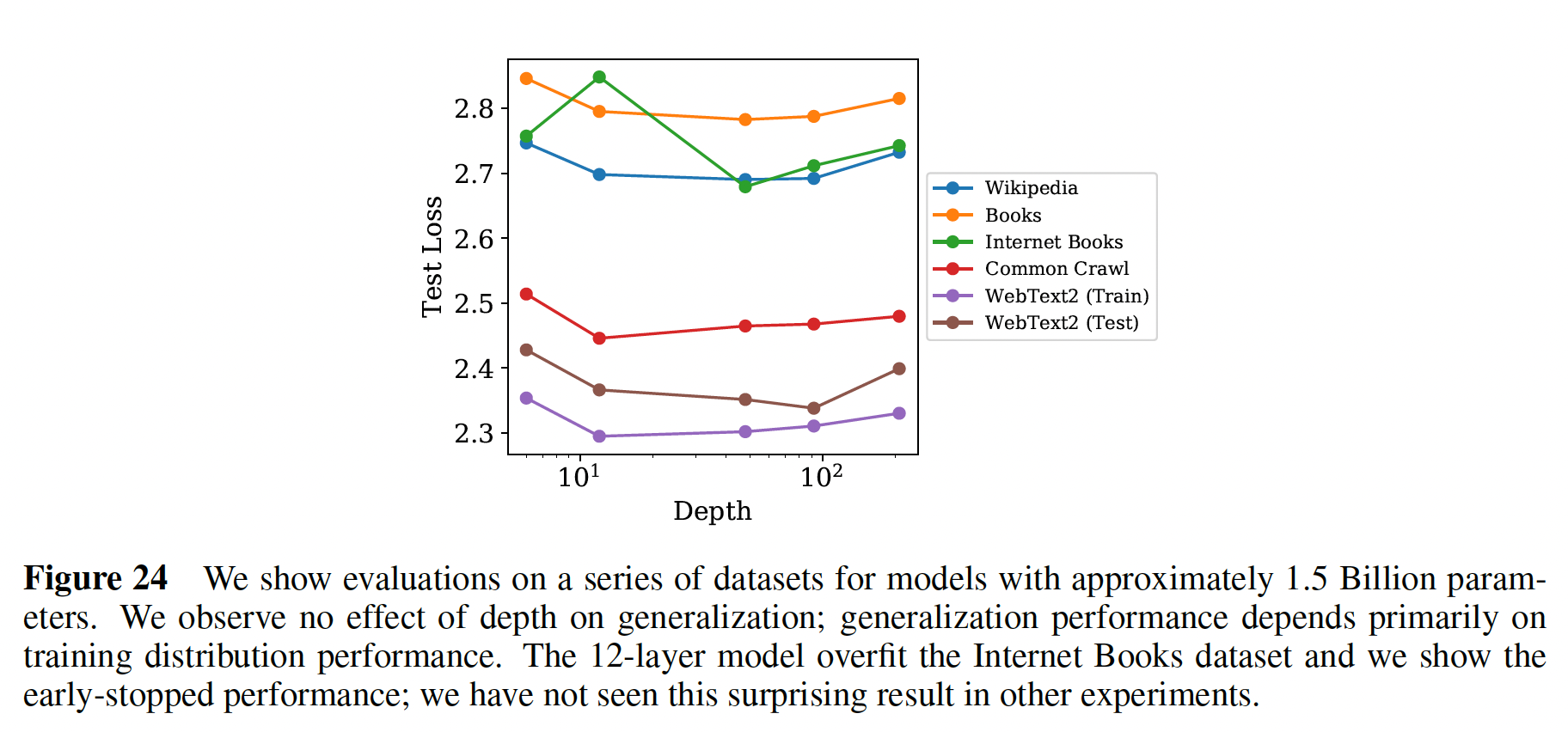
d. 性能与数据集大小和计算量的关系
我们在下图中显示了
test loss作为数据集大小token数量为单位)和训练计算量对于
WebText2数据集的固定子集上训练了一个test loss不再减少,我们就停止训练。我们看到,所产生的test loss可以用数据集大小如
Figure 1中间的图所示。训练过程中使用的
non-embedding计算总量可以估计为batch size,parameter updates的数量,系数6代表了同时包含前向传播和反向传播。因此,对于一个给定的step数量请注意,在这些结果中,
batch size这个结果如
Figure 1左图的加粗黑线所示。它可以用如下的方程来拟合:此外,在左图中还包括每个模型的学习曲线,从而展示每个模型何时达到最优。

我们将在后面更仔细地研究计算量的最佳分配问题。数据强烈表明,
sample efficiency随着模型的大小增加而提高,如右图所示,对于给定的test loss,模型越大所需要的样本数越少。左图:每条曲线表示在给定的
test loss(不同曲线采用不同的值)的条件下,最短的训练时间(由minimum steps衡量)和模型大小的关系。通常而言,模型参数越大,训练时间越短。右图:每条曲线表示在给定的
test loss(不同曲线采用不同的值)的条件下,最少的训练过程中看过的样本(
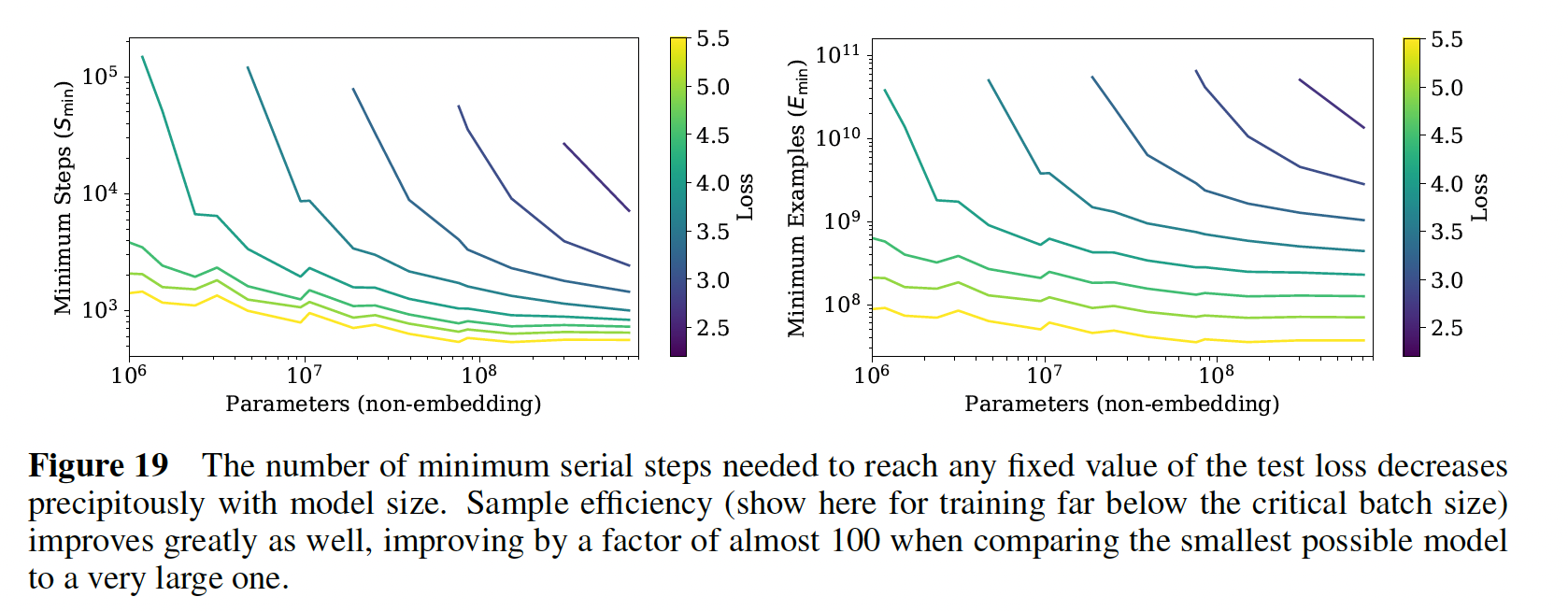
43.3 Infinite Data Limit 和过拟合
在前面的内容中,我们发现了针对语言建模性能的一些
basic scaling laws。这里,我们将研究在具有tokens的数据集上训练的大小为test loss符合公式scaling law。这为我们需要多少数据来训练规模不断扩大的模型、并同时控制过拟合提供了指导。
43.3.1 L(N, D) 公式
我们选择参数化
其中,这个公式基于三个原则:
词表大小或
tokenization的变化有望通过一个整体因子来rescale损失函数。loss的建模)自然必须考虑到这种rescaling。固定
overall loss应该接近overall loss应该接近analytic的,因此它在series expansion)。对这一原则的理论支持明显弱于前两者。即,对于无限的训练数据,模型应该能够收敛。
我们选择的
rescale因为当
test loss停止改善时我们提前结束训练,并且我们以相同方式优化所有模型,所以我们期望较大的模型应该总是比较小的模型表现得更好。但是对于固定的、有限的possible loss。类似地,具有固定大小的模型将是容量有限的。这些考虑激发了我们的第二个原则。注意,关于在第三个原则更加是推测性的。一个简单而普遍的原因是,在非常大的
《High-dimensional dynamics of generalization error in neural networks》),这与loss扩展到correction在其他方差来源中占主导地位,例如有限的batch size、efficacy of optimization的其他限制。没有经验的证实,我们对它的适用性没有信心。我们的第三个原则解释了公式
在任何情况下,我们都会看到,我们对于
43.3.2 拟合结果
我们以
10%的dropout rate来正则化我们的所有模型,然后跟踪test loss,一旦test loss不再下降时我们就停止训练。实验结果如Figure 9左图所示,它包含了针对公式Figure 9左图:每条曲线代表一个data size,给出了在该data size的条件下,test loss和Figure 9右图:
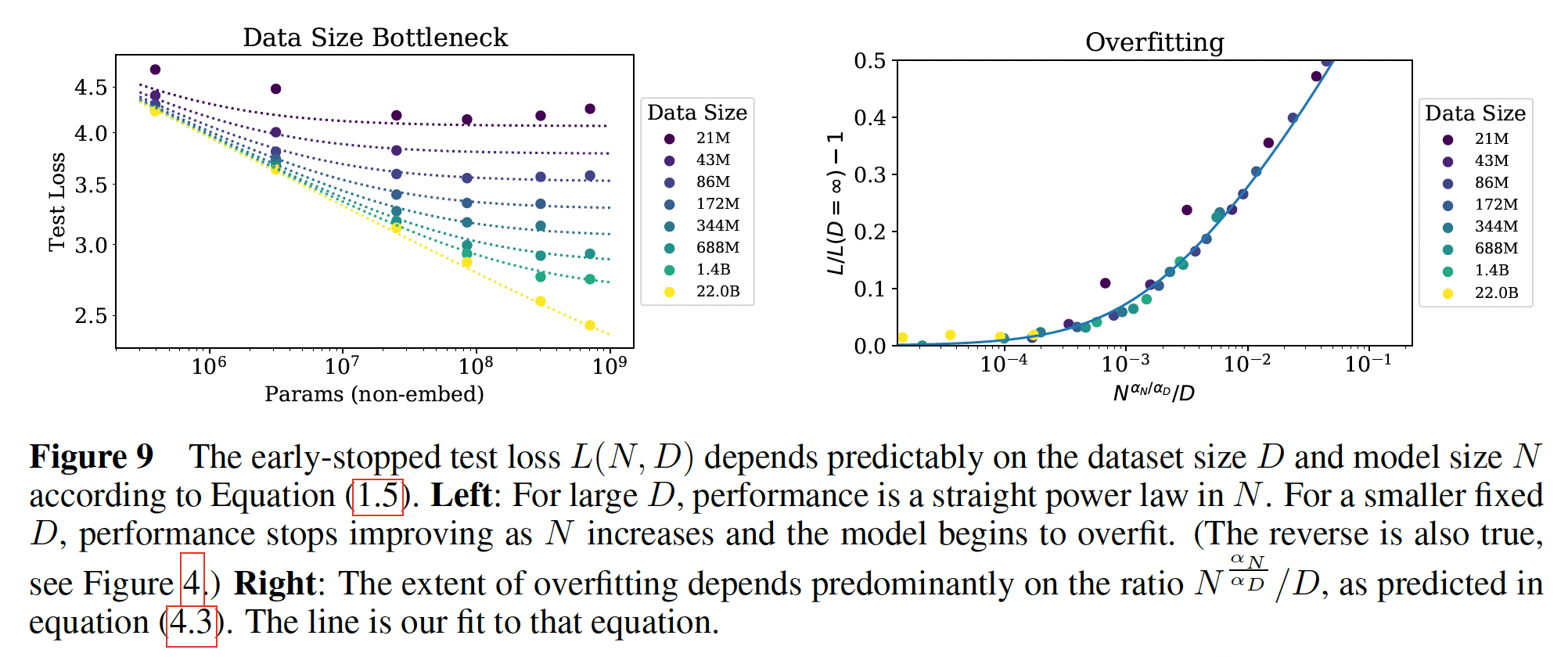
我们获得了极好的拟合,除了如下的
runs:数据集已经减少了1024倍到大约tokens。对于如此小的数据集,一个epoch仅包含40次参数更新。也许这样一个微小的数据集代表了语言建模的一个不同的区域,因为过拟合在训练的早期就发生了 (Figure 16右图的第一条Test Loss曲线)。还要注意,这些参数与basic power laws中获得的参数略有不同,因为这里我们拟合的是完整的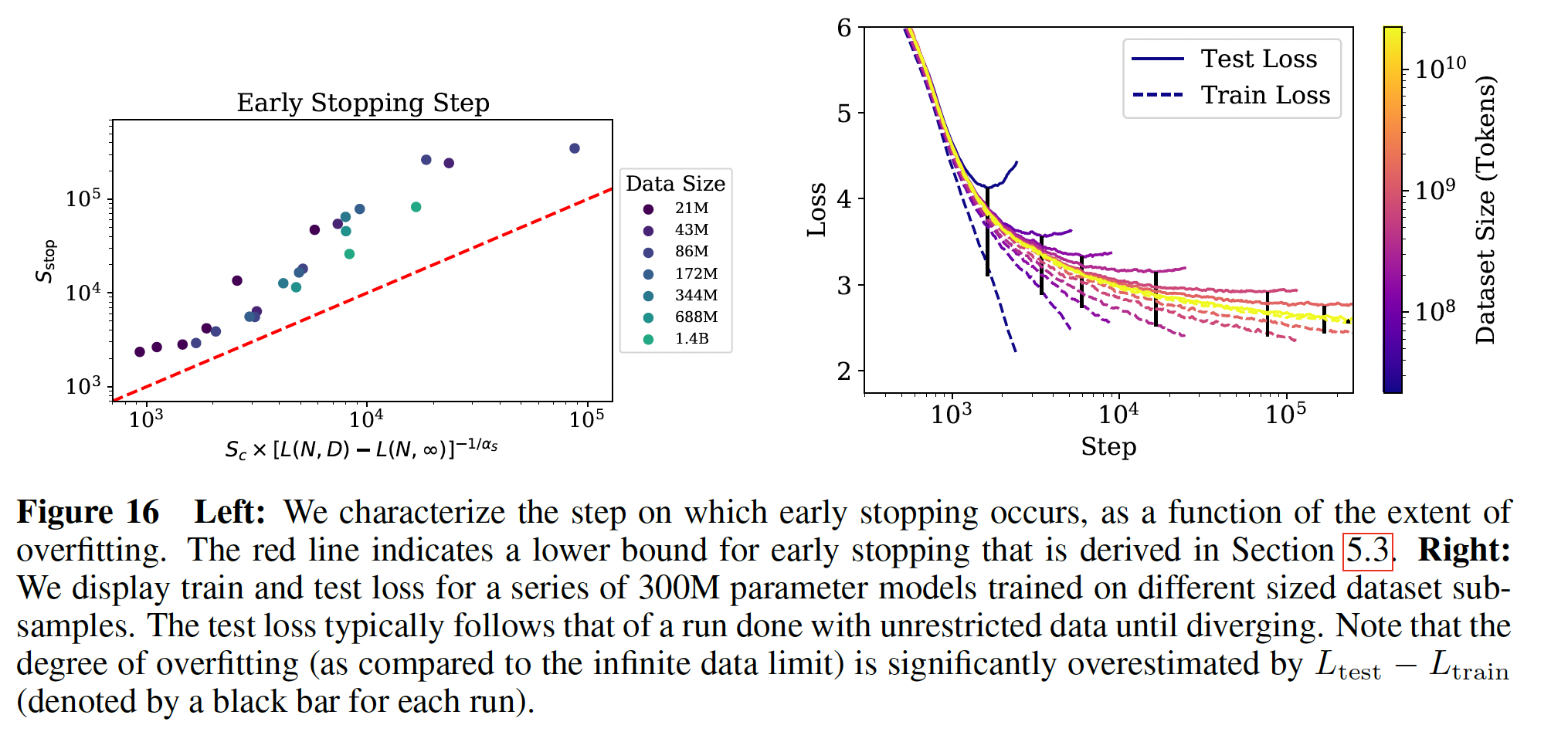
43.3.3 D 和 N 之间的亚线性关系
为了绘制
infinite data limit的边界,我们可以直接研究过拟合的程度。对于除了最大的模型之外的所有模型,当用完整的22B token的WebText2数据集训练时,我们没有看到过拟合的迹象,因此我们可以将其作为infinite data limit:并把它作为
Figure 9右图所示。这是根据等式scaling law得出的,即:根据
注意,在大的
test loss,它是test loss。因此:0。如Figure 9右图所示。
对于不同的随机数种子,我们估计
loss的方差大约为0.02,这意味着,为了避免过拟合,我们需要:推导过程:
利用这种关系,小于
22B token的WebText2数据集上被训练从而具有最小的过拟合,但是我们最大的模型将会遇到一些轻微的过拟合。更一般地,这种关系表明数据集大小可以关于模型大小成亚线性增长,同时避免过拟合。然而,请注意,这通常并不代表compute-efficient training。我们还应该强调,在改变数据集和模型大小时,我们没有
optimized regularization(例如,dropout rate)。
43.4 关于模型大小和训练时间的 scaling laws
在本节中,我们将证明一个简单的
scaling law可以很好地描述loss作为模型大小首先,我们将解释如何使用
《An empirical model of large-batch training》的结果来定义universal training stepbatch size下训练的事实。然后,我们将证明我们可以使用公式
loss与模型大小和训练时间。稍后,我们将使用这些结果来预测模型大小和训练时间之间关于训练计算量的最佳分配,然后确认该预测。
43.4.1 临界 Batch size
在
《An empirical model of large-batch training》中提出了一个关于训练的batch size依赖性的简单的经验理论。该论文认为,对于training,有一个临界batch size对于
batch sizecompute-efficiency的下降非常小。而对于
该论文还认为,
gradient noise scale为gradient noise scale也不直接依赖于模型大小,而是依赖于已经获得的loss value。这些结果可用于预测训练时间和计算量将如何随batch size而变化。为了尽可能有效地平衡训练时间和计算量,最好使用batch size为training steps数量,而在即:大的
batch size可以节省训练时间、但是浪费了计算量;小的batch size可以节省计算量、但是浪费了计算时间。更具体地,可以证明对于各种各样的神经网络任务, 当训练到
losstraining steps数量processed数据样本数量其中:
training steps数量,而注意:
我们在下图中展示了针对
Transformer的这种关系(即,test loss。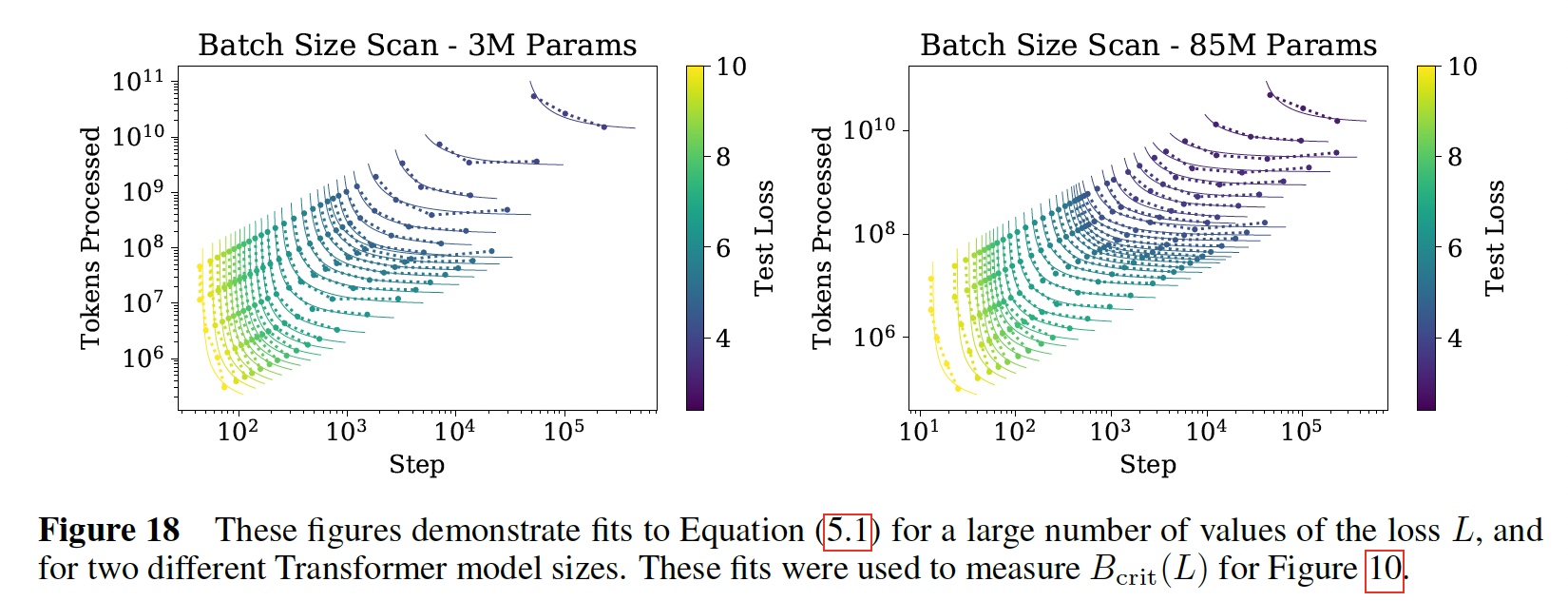
这个关系定义了临界的
batch size:它是目标损失值的函数。在临界
batch size的训练可以实现大致最优的time/compute tradeoff,需要training steps、以及处理在下图中,我们绘制了两个不同模型的临界
batch size和gradient noise scale,作为training loss的函数。我们看到,loss《An empirical model of large-batch training》的prediction继续适用于Transformer语言模型。临界batch size在loss上符合幂律:其中:
为什么选择这样的拟合公式?因为随着
loss接近其最小值gradient noise scale预计会发散,并且我们期望noise scale。因此随着注意:下图中,横轴的右侧为零。
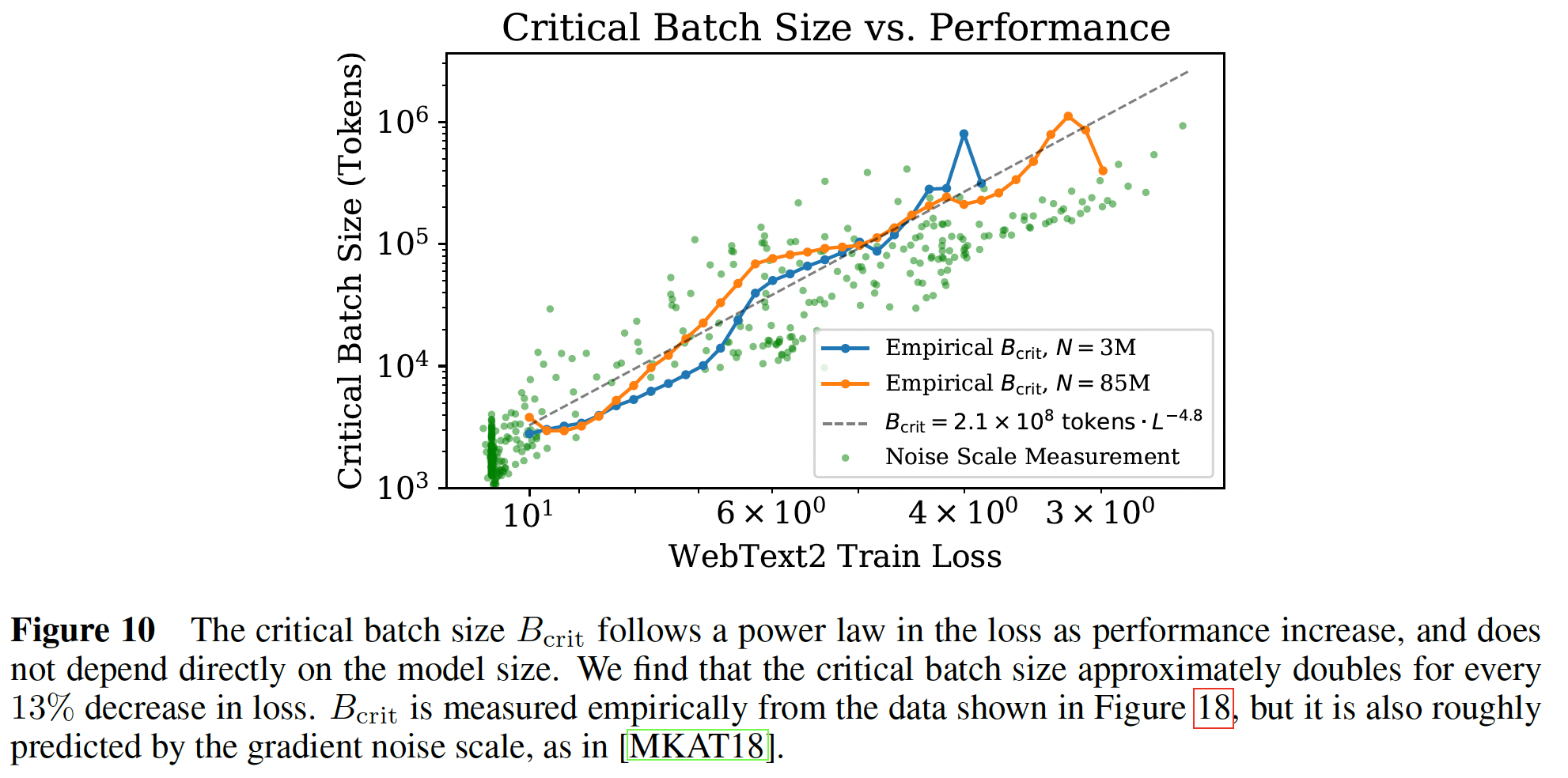
如果我们在
losstraining steps数量的临界值定义为:推导过程:根据定义
推导过程中并未要求
该式子的物理意义:
根据
batch sizetraining step另一方面,任意选择一个
batch sizetraining step
如果我们在
loss其中:
batch sizenon-embedding计算量。推导过程:根据定义
根据
推导过程中并未要求
43.4.2 关于模型大小和计算量的性能
现在,我们将使用定义的
infinite data limit下,loss对模型大小和训练时间的依赖性的简单且通用的拟合。对于loss,我们将使用公式Adam优化的training runs,即:我们纳入了
learning rate schedule的warmup阶段后的所有training steps,并找到了拟合数据的参数: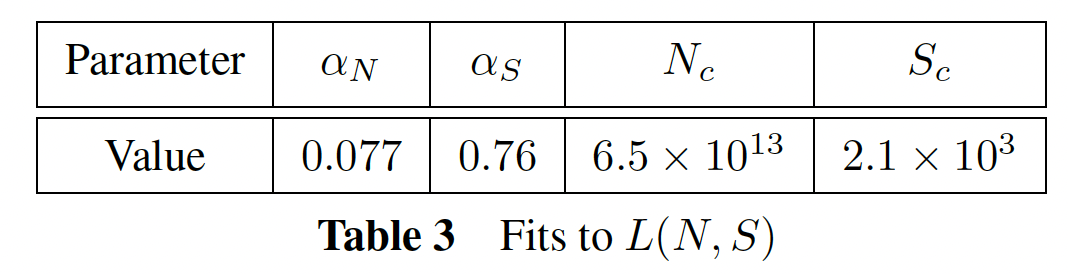
有了这些参数,我们获得了右图中的学习曲线的拟合。尽管拟合并不完美,但我们相信,鉴于方程
右图中,每条曲线对应固定模型大小条件下不同
test loss。loss对power-law dependence反映了optimizer dynamics和loss landscape的相互作用。由于拟合曲线在训练后期是最好的,此时loss可能近似为二次方程,power-law应该提供关于loss的Hessian谱的信息。它的普遍性表明,Hessian eigenvalue density大致独立于模型大小。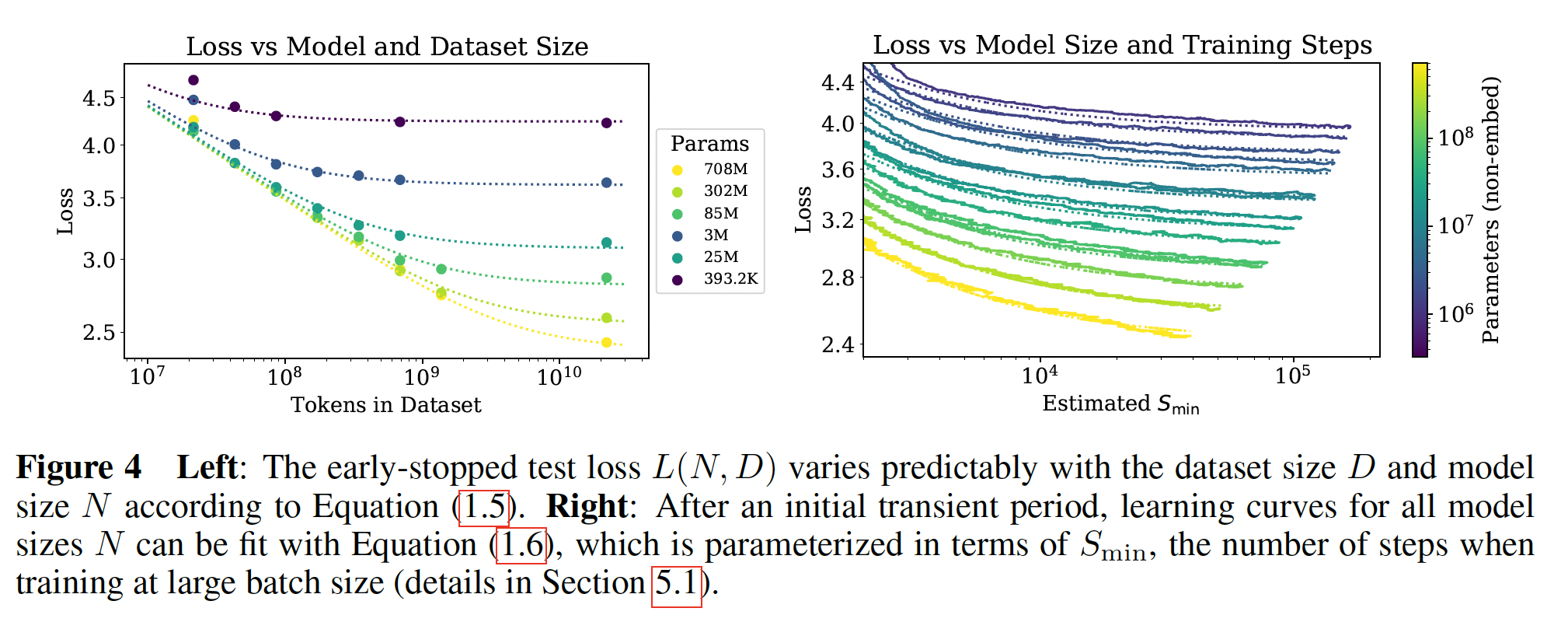
数据和拟合可以以不同的、更有趣的方式可视化,如下图所示。在此,我们研究了作为模型大小的函数的
test loss,同时固定了训练中使用的总的non-embedding computetraining steps数量左图:每条曲线给出了固定计算预算条件下
test loss和模型大小的关系;右图:每条曲线给出了固定
steps条件下test loss和模型大小的关系;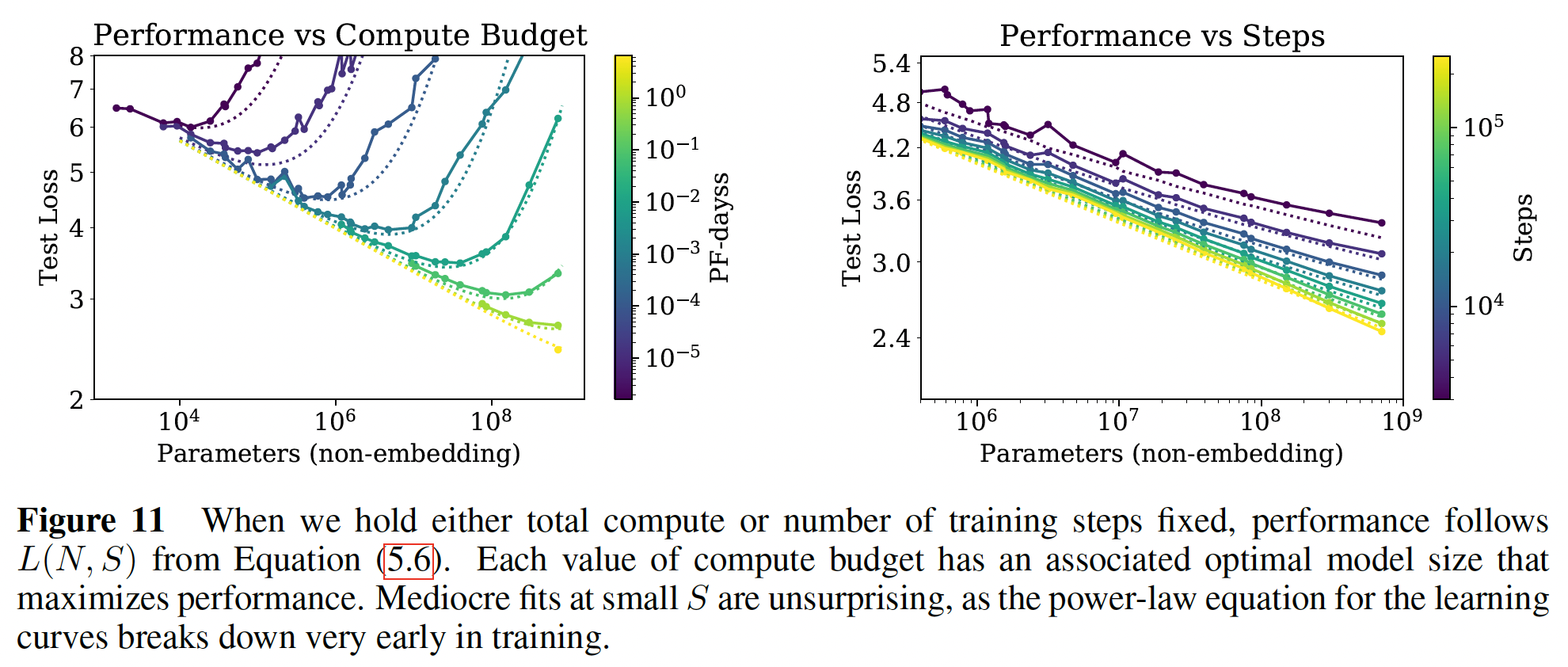
43.4.3 Early Stopping Step 的下限
training step数量的下限(粗略的估计),其中在data limited训练中出现了早停。它的动机是这样的思想,对于给定的模型,有限的correction成比例。这将低估test loss将下降得更慢,因此我们将需要更多的training steps数量来达到在有限的test loss。这个推理方向导致了不等式:其中:
分母代表过拟合的程度,其中
test loss(代表没有过拟合)。过拟合程度越少,那么这个公式似乎不是推导而来,而是经验公式。
左图显示了这个不等式及其与经验数据的比较。在该图中,

43.5 计算量预算的最优分配
我们在
Figure 1的右上角显示了性能的经验趋势作为训练计算量的函数。然而,这一结果涉及固定batch sizebatch size在本节中,我们将针对这一疏忽进行调整。更重要的是,我们将使用前面的结果来确定模型大小

43.5.1 最优性能和分配
从公式
loss作为最优分配计算量Figure 1的计算量图相比,新的关于橙色曲线为
Figure 1的左图也是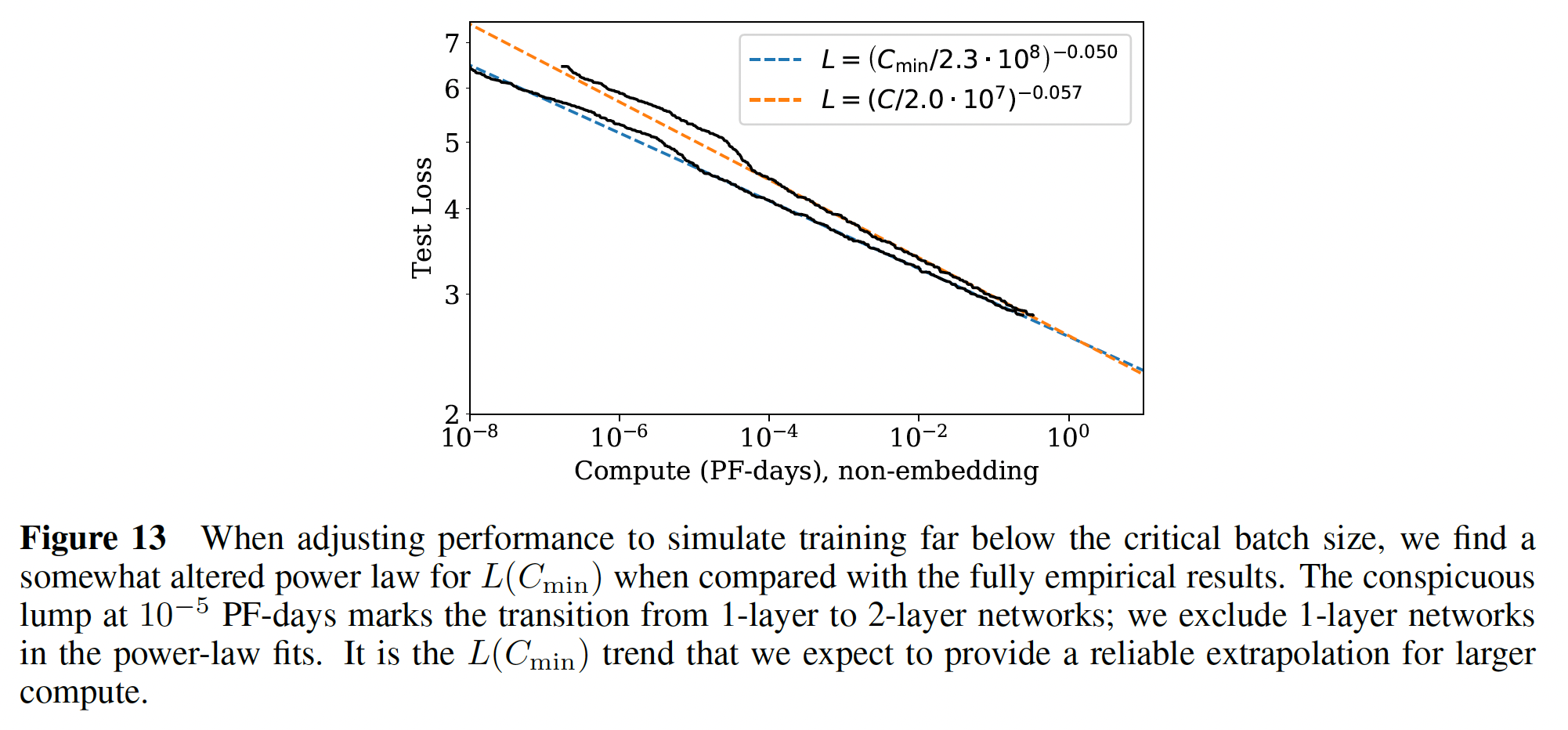
给定
loss。最佳模型尺寸如下左图所示。我们观察到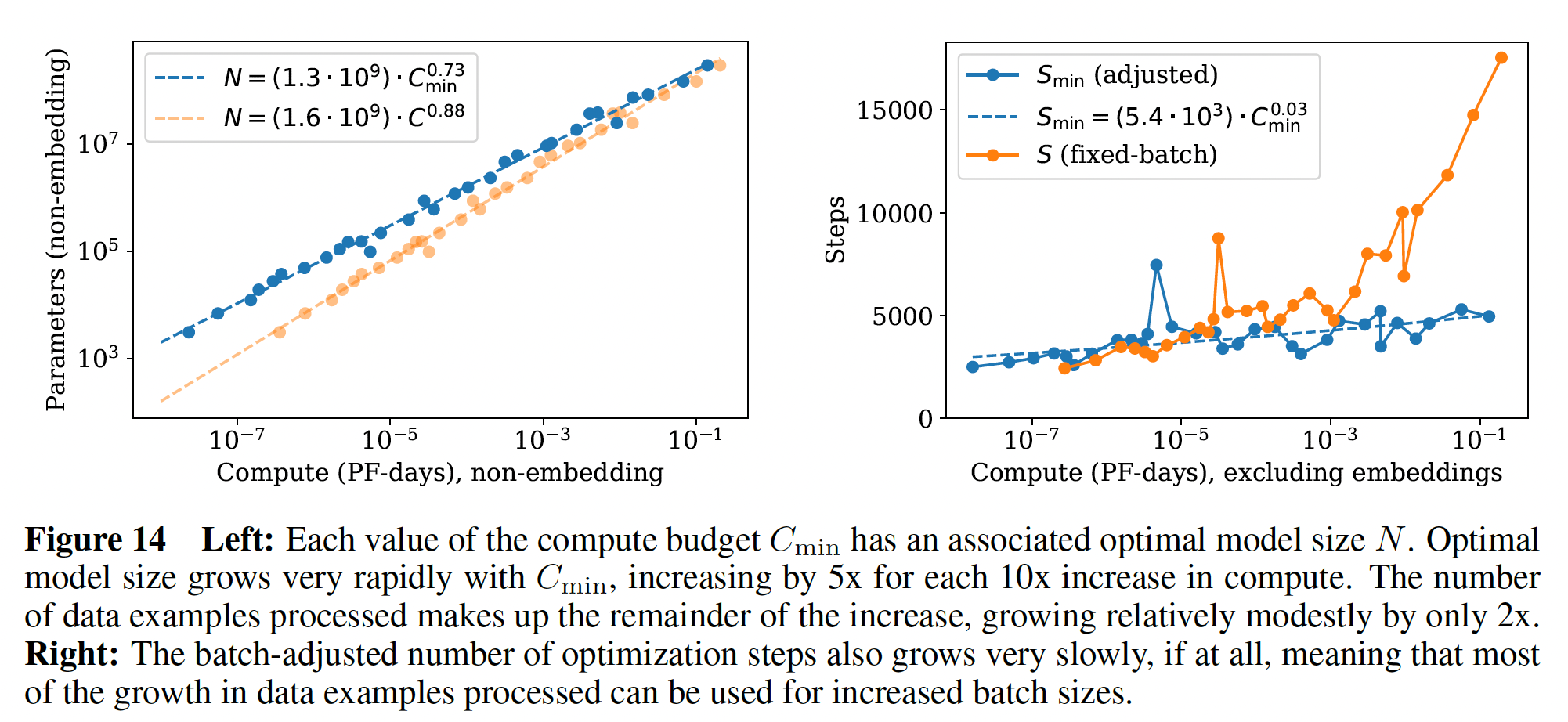
在下图中,我们展示了次优
model size来训练模型的效果。左图,次优
model size导致更多的计算量(相对于最佳计算量)。右图,更大
model size导致更少的计算时间(相对于最佳计算时间)。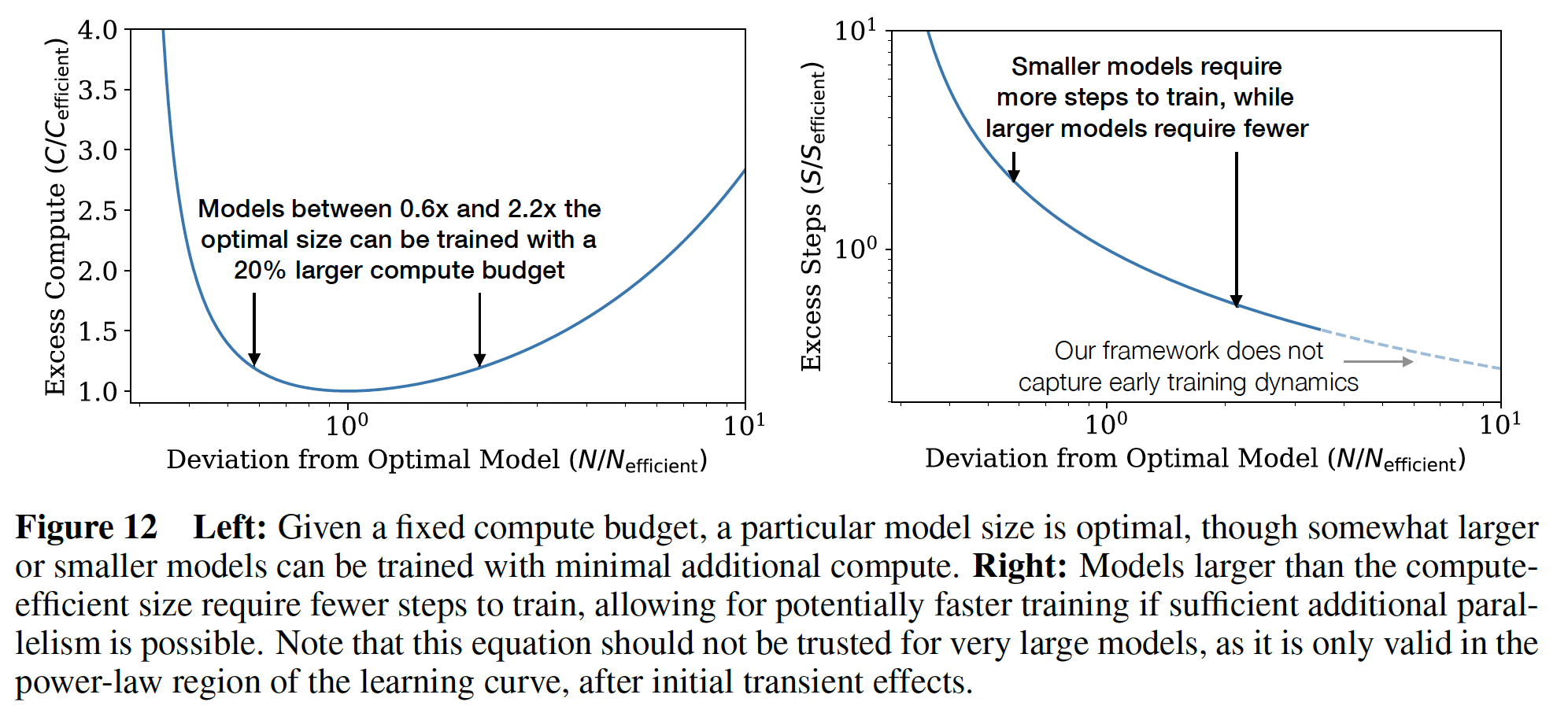
通过定义
这使我们得出结论,随着计算量的增加,最佳
training steps数量只会非常缓慢地增长,因为Figure 14中右图的经验结果相匹配。事实上,measured exponent足够小,我们的结果甚至可能与指数为零相一致。由于
因此,我们的结论是:当我们以最佳计算量分配来
scale up语言模型时,我们应该主要增加模型大小scale upbatch size为serial steps数量增加可以忽略不计。由于compute-efficient training使用相对较少的optimization steps,因此可能需要进行额外的工作来加速早期的training dynamics。
43.5.2
allocation的结果可以从方程loss作为对于
loss作为训练计算量的函数,我们预测:其中:
与下图中的指数非常一致。
下图中的指数是
-0.050,而这里的指数是-0.054,存在一定的gap。因为它们是用不同的公式来预测的。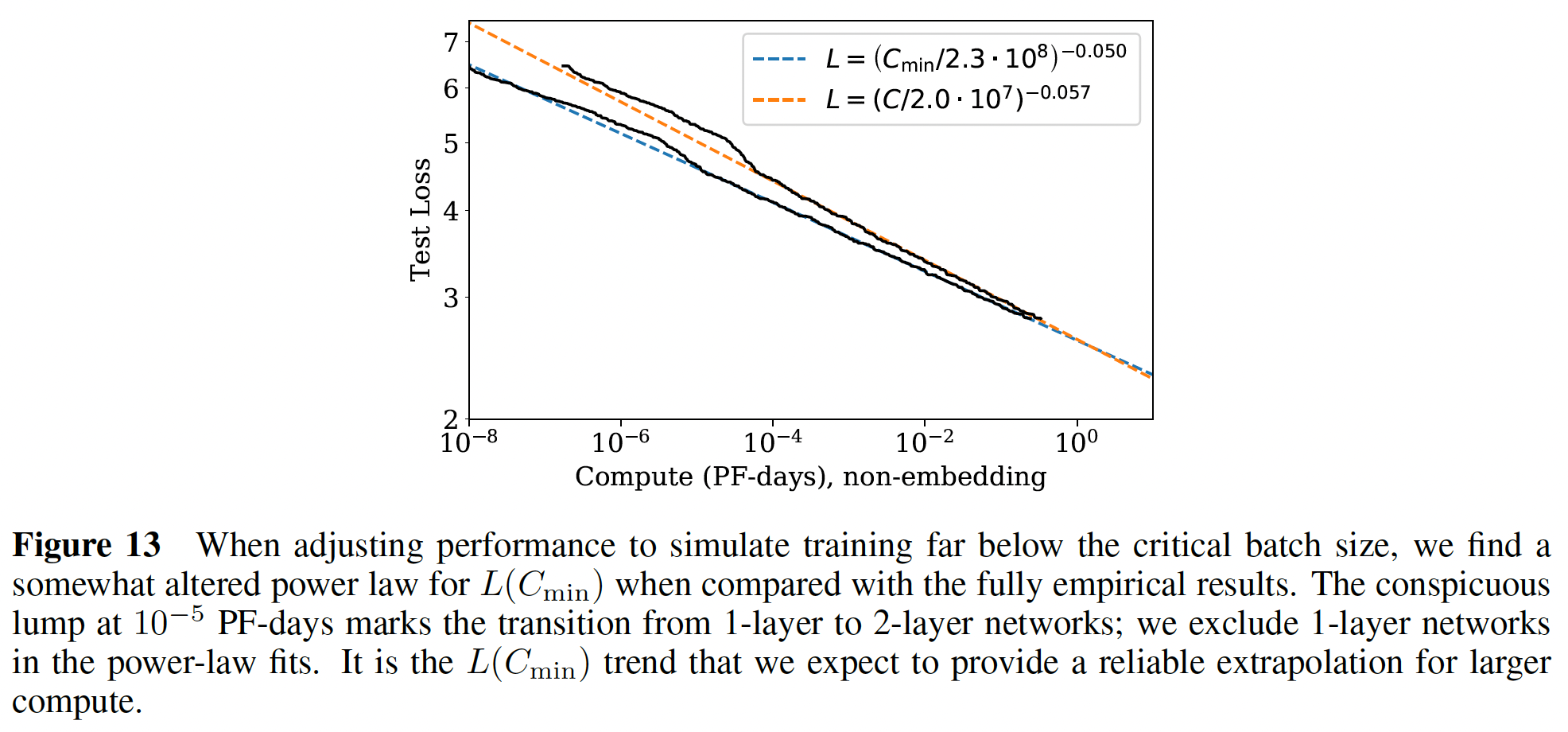
我们还预测到:
这也和下图中的
scaling相匹配,在几个百分点之内。前面已经得到
gap。因为它们是用不同的公式来预测的。我们的
scaling laws为语言建模的性能提供了一个预测性的框架。
43.5.3 矛盾和猜想
我们观察到,在计算量、数据量或模型大小的大数值下,没有偏离直接的
power-law趋势的迹象。不过,我们的趋势最终必须趋于平稳,因为自然语言具有非零的熵(即,test loss不可能降低到零)。事实上,本节中描述的
compute-efficient training的趋势已经包含了一个明显的矛盾。在比这里记录的规模高几个数量级的时候,scaling law所预测的性能会下降到低于应该有的水平。这意味着我们的scaling laws必须在这一点之前崩溃,但是我们猜测这个交点有更深的含义:它提供了Transformer语言模型达到最大性能的一个估计值。由于
compute-efficient training所使用的数据量随着计算预算的增加而缓慢增长,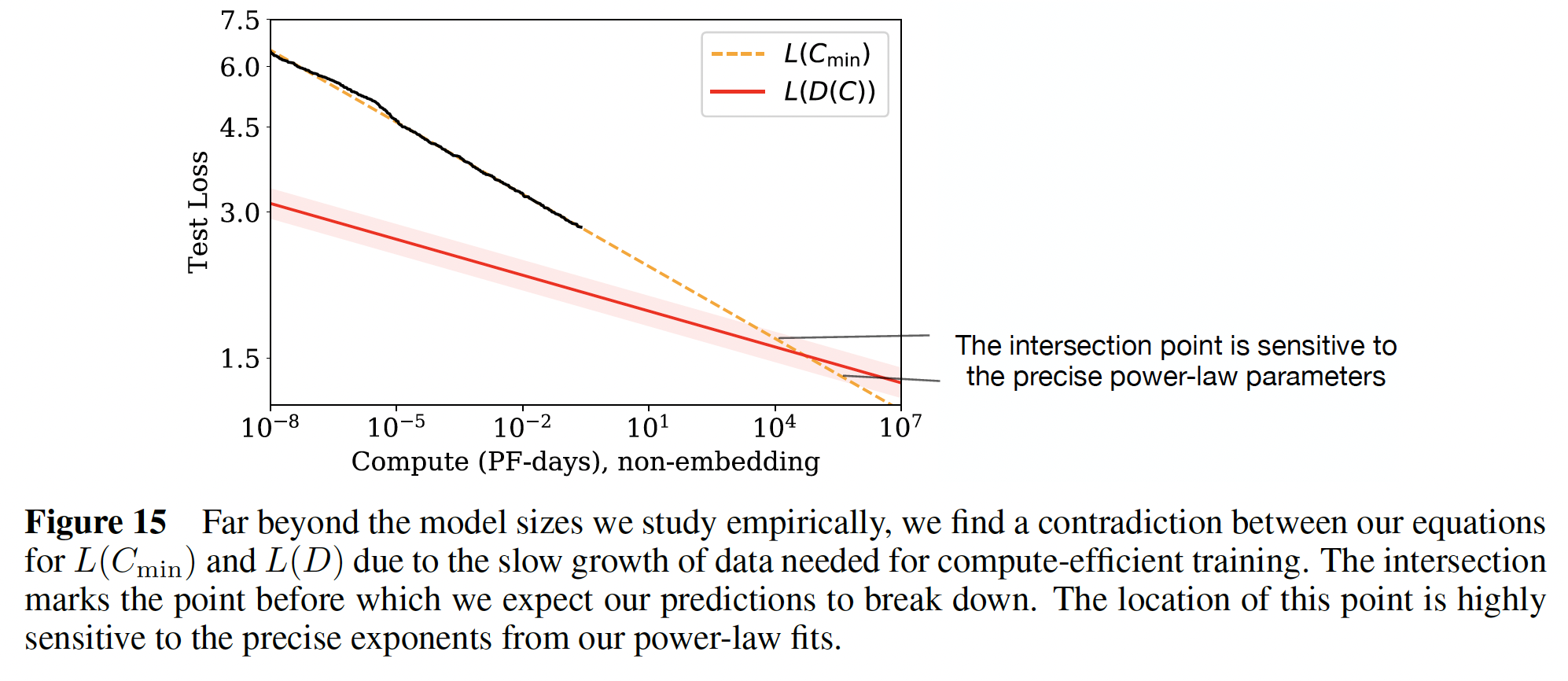
为了控制过拟合,前面的结果意味着我们应该将数据集的规模扩大为:
其中,我们使用了
Figure 14中的compute-efficient让我们将其与
compute-efficient training的数据要求进行比较。如果我们以临界batch size(即这是数据集大小能够随着计算量而有效增长的最大速度,因为它意味着我们只训练一个
epoch。但它比方程compute-efficient training最终会遇到过拟合的问题,即使训练过程中从未重复使用任何数据。根据
Figure 1,我们期望当我们受到数据集大小的瓶颈时(即过拟合),loss的scale应该是loss将随着计算量的进行而scale为Figure 13中对scaling尽管数值是非常不确定的,在任何一个方向都会有一个数量级的变化,这取决于
power-law拟合的指数的精确值。最明显的解释是,我们的scaling law在达到这一点时或之前就已经崩溃了,而这一点在计算量和模型大小上都还有很多数量级。人们也可以猜想,这个交叉点有更深的含义。在相同数据要求的条件下,如果我们没有将模型规模增加到
entropy-per-token提供一个粗略的估计。在这种情况下,我们期望loss的趋势在我们可以通过考虑添加了噪音的训练数据集的版本来猜测平缓之后的
tokens,从而人为地用一个恒定的additive factor来提高损失。然后,与noise floor的距离
43.6 结论
43.6.1 总结
我们
Transformer语言模型的主要发现如下:模型性能强烈依赖于模型规模,弱依赖于
model shape: 模型的性能最强烈地依赖于模型规模,它包括三个因素:模型参数的数量embedding参数)、数据集的大小dpeth与width。注意,这里的模型性能是在测试集上评估的。
平滑的幂率(
smooth power laws):模型性能与三个scale factorN/D/C非常大时,并没有偏离这些趋势的迹象,尽管在达到zero loss之前,模型性能最终必须趋于平缓。
过拟合的普遍性: 只要我们同步
scale upperformance penalty)可预测地取决于8倍,我们只需要增加大约5倍的数据就可以避免惩罚。training的普遍性: 训练曲线(training curve)遵循可预测的幂律,其中训练曲线大致上与模型大小无关。通过推断训练曲线的早期部分,我们可以大致预测如果我们训练的时间更长,将会取得什么样的loss。transfer提高测试性能:当我们在与训练时分布不同的文本上评估模型时,评估结果与验证集上的结果密切相关,loss的偏移量大致不变。换句话说,迁移到一个不同的分布上会产生一个恒定的惩罚,但其他方面的改善与训练集上的表现大致一致。样本效率(
sample efficiency):大模型比小模型更具有样本效率,以更少的optimization step(Figure 2左图)和更少的数据点(Figure 4左图)达到相同的性能水平。此外,
Figure 19提供了另一种观察这一现象的方法,它显示了不同模型达到各种固定loss的时间。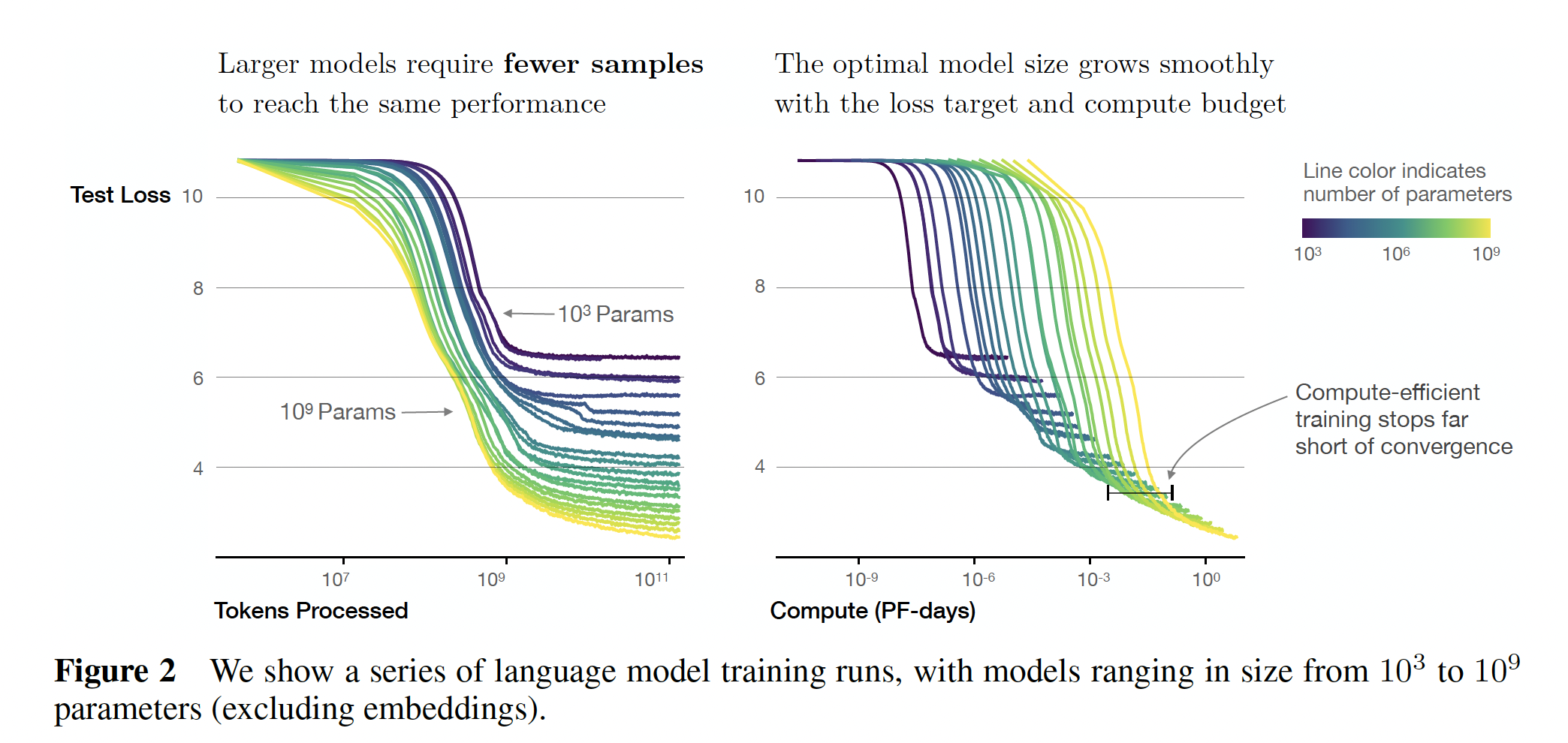


收敛是低效的: 当在固定的计算预算
Figure 3)。因此,与人们的预期相反,相比于训练小模型并收敛,这种方式得到的最佳compute-efficient training要更加sample efficient。随着训练计算量的增加,数据需求增长非常缓慢: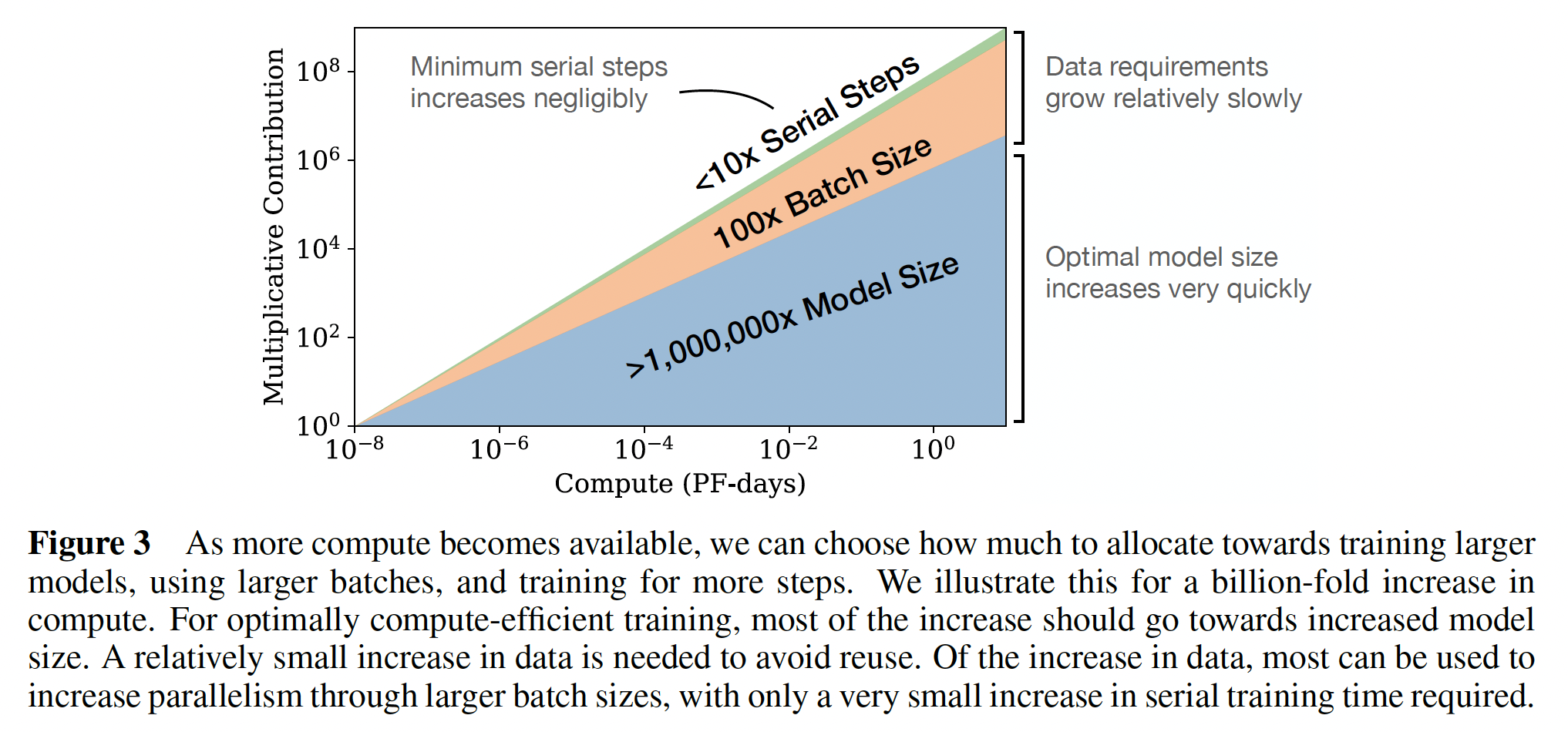
最优的
batch size:训练这些模型的最优的batch size大约仅仅是loss的幂次,并通过测量gradient noise scale来确定。对于我们可以训练的最大的模型,在收敛时大约是1M ~ 2M个tokens。
综合来看,这些结果表明,当我们适当地
scale up模型规模、数据规模、以及计算量时,language modeling的性能会平稳地、可预测地提高。我们预计,更大的语言模型将比目前的模型表现得更好、更加sample efficient。
43.6.2 Scaling Laws 摘要
当性能仅仅受
non-embedding parameters数量optimally allocated计算预算Transformer的loss(如Figure 1):对于参数数量
对于大型模型(即,
对于最佳规模的模型(即,
batch size(对计算量的最佳使用),在计算量
这些关系在
8个数量级、6个数量级、以及2个数量级上都成立。它们非常弱地依赖于model shape和其他的Transformer超参数(depth、width、自注意头的数量),具体数值与Webtext2训练集相关。幂率
loss要更小,其中大约是原始loss的vocabulary size和tokenization,因此没有基本的含义(fundamental meaning)。critical batch size决定了数据并行的speed/efficiency tradeoff,也大致服从公式
这个方程与
Figure 4的左图相配合。我们猜想,这种函数形式也可以为其他generative modeling task来参数化trained log-likelihood。当在
infinite data limit中对一个给定的模型进行有限的parameter update stepsFigure 4的右边):其中:
optimization steps(即参数更新次数)的数量,batch size。当在固定的计算预算
batch sizestep数这与经验结果(
随着计算预算
Figure 3)。这也意味着,随着模型的增大,它们的sample efficient也越来越高。在实践中,研究人员通常训练较小的模型(由于硬件的限制),较小模型的训练时间要更长(相比较于最大化计算效率的模型,即更大的模型)。最佳性能取决于总计算量的幂律(参考方程我们为方程
learning curve fit及其对训练时间的影响进行了分析,并对我们每个token的结果进行了细分。我们还对LSTM和recurrent Transformer做了一些简单的比较。公式总结:
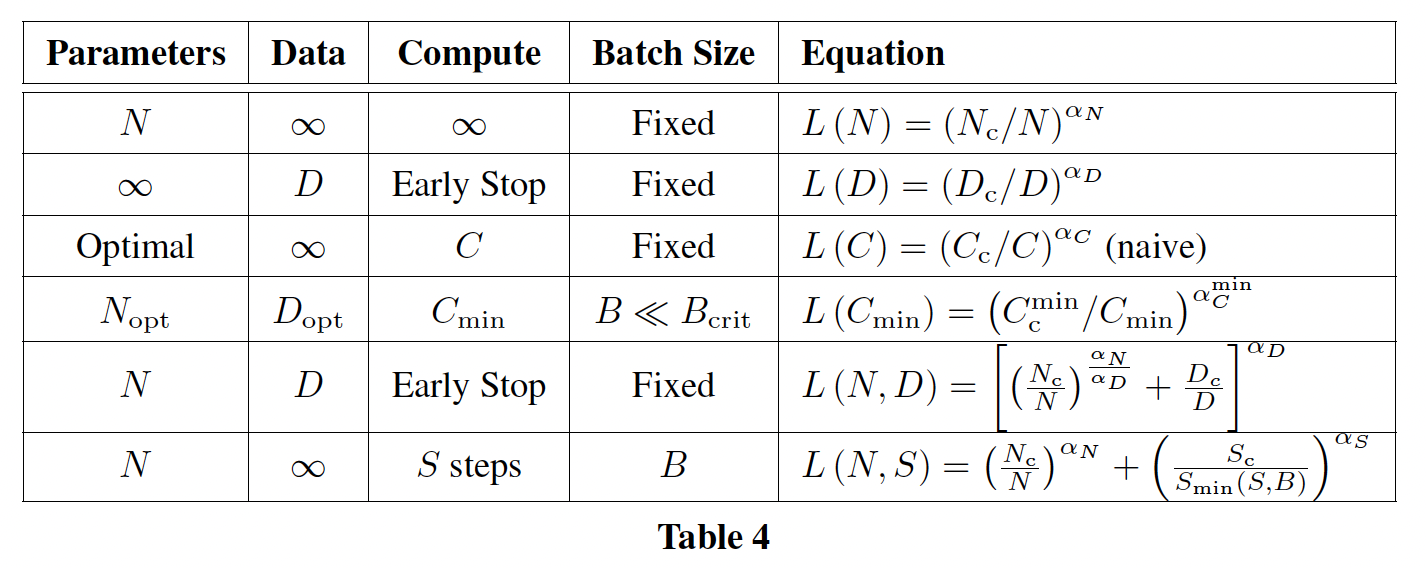
这些趋势的经验拟合参数为:
compute efficient training的最优参数为: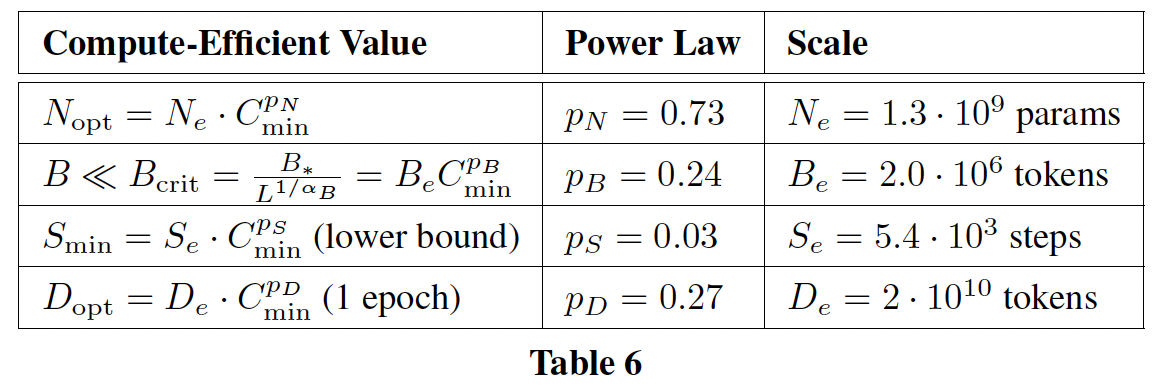
43.6.2 注意事项
在这一节中,我们列出了一些对我们的分析可能存在的注意事项:
目前,我们对我们提出的任何一个
scaling laws都没有一个坚实的理论理解。与模型大小和计算量的scaling关系尤其神秘。通过用一个noisy的二次方来建模loss,在模型大小固定的情况下,也许有可能理解在非常大的scaling关系,以及在训练后期的学习曲线的形状。但是在非常大的模型大小下,与scaling关系仍然是神秘的。如果没有一个理论、或者对我们的scaling laws的修正有一个系统的理解,就很难确定在什么情况下它们可以被信任。我们对远在我们所探索的范围之外的
loss的serial training steps数量之间的权衡产生重大影响,这将对训练时间产生重大影响。我们没有彻底研究小数据的区域,对于最小的
epoch只有40个step),我们对我们使用了估计的训练计算量
scaling可能不太准确。我们调优了学习率,并且采用了
learning rate schedule进行实验。但是我们可能忽略了调优一些对scaling有重要影响的超参数(如intialization scale或动量)。学习率的最佳选择对
target loss是敏感的。当训练接近收敛时,可能需要使用较小的学习率来避免发散。但是当进行short training run时(例如由于计算限制),可能会使用较大的学习率。对于没有进行收敛的training runs, 我们没有进行更高学习率的实验。
四十四、Chinchilla[2022]
《Training Compute-Optimal Large Language Models》
最近,一系列大型语言模型(
Large Language Model: LLM)被引入,目前最大的稠密语言模型拥有超过500B参数。这些大型自回归transformer模型在许多任务上使用各种评估协议(如zero-shot、few-shot和fine-tuning),都表现出令人印象深刻的性能。训练大型语言模型的计算成本和能源成本很高,并随着模型规模的增加而上升。在实践中,分配的
training compute budget通常是事先知道的:有多少个accelerators可用,以及用多久。由于这些大型模型通常只训练一次,因此准确估计给定computational budget条件下的最佳模型超参数至关重要(《Scale efficiently: Insights from pre-training and fine-tuning transformers》)。《Scaling laws for neural language models》表明:自回归语言模型的参数数量与它的性能之间存在幂律(power law)关系。因此,该领域一直在训练越来越大的模型,并预期带来性能的提高。《Scaling laws for neural language models》的一个值得注意的结论是:大型模型不应该被训练到其最低的损失(test loss),以达到compute optimal。虽然我们得出了同样的结论,但我们估计大型模型的训练应该比作者建议的多得多的training tokens。具体来说,在computational budget增加十倍的情况下,他们建议模型的大小应该增加5.5倍,而training tokens的数量只应该增加1.8倍。相反,我们发现模型的大小和training tokens的数量应该以相等的比例进行scale。《Scaling laws for neural language models》的结论:当计算预算增加十倍时,模型大小需要增加
training tokens数量为遵循
《Scaling laws for neural language models》和GPT-3的训练设置,最近训练的许多大型模型已经训练了大约300B token(如下表所示),这与增加计算量时主要增加模型规模的做法是一致的。
在这项工作中,我们重新审视了这个问题: 在固定的
FLOPs预算下,应该如何权衡模型大小和training tokens数量?为了回答这个问题,我们将最终的预训练损失training tokens数量computational budgetseen training tokens数量其中:
computational budget注意:这里的
training tokens数量,这跟《Scaling Laws for Neural Language Models》中的符号不同。在《Scaling Laws for Neural Language Models》中,tokens数量,training tokens数量。这里的
test loss。我们根据
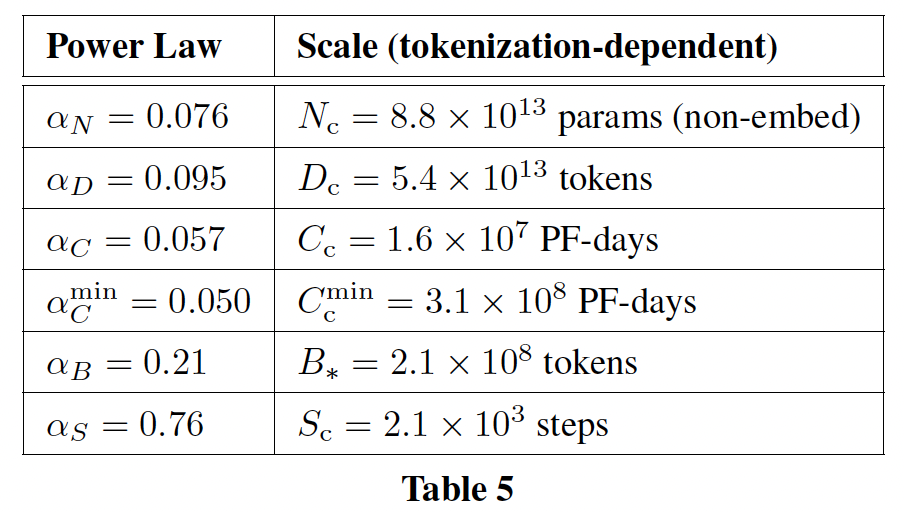
400多个模型的loss来经验性地估计这些函数,这些模型的参数规模从低于70M到超过16B,并在从5B到超过400B个token上进行训练,每个模型配置都在几个不同的training horizons进行训练。我们的方法导致了与《Scaling laws for neural language models》的结果大不相同。我们在下图中强调了我们的结果,并在后面章节中强调了我们的方法有什么不同。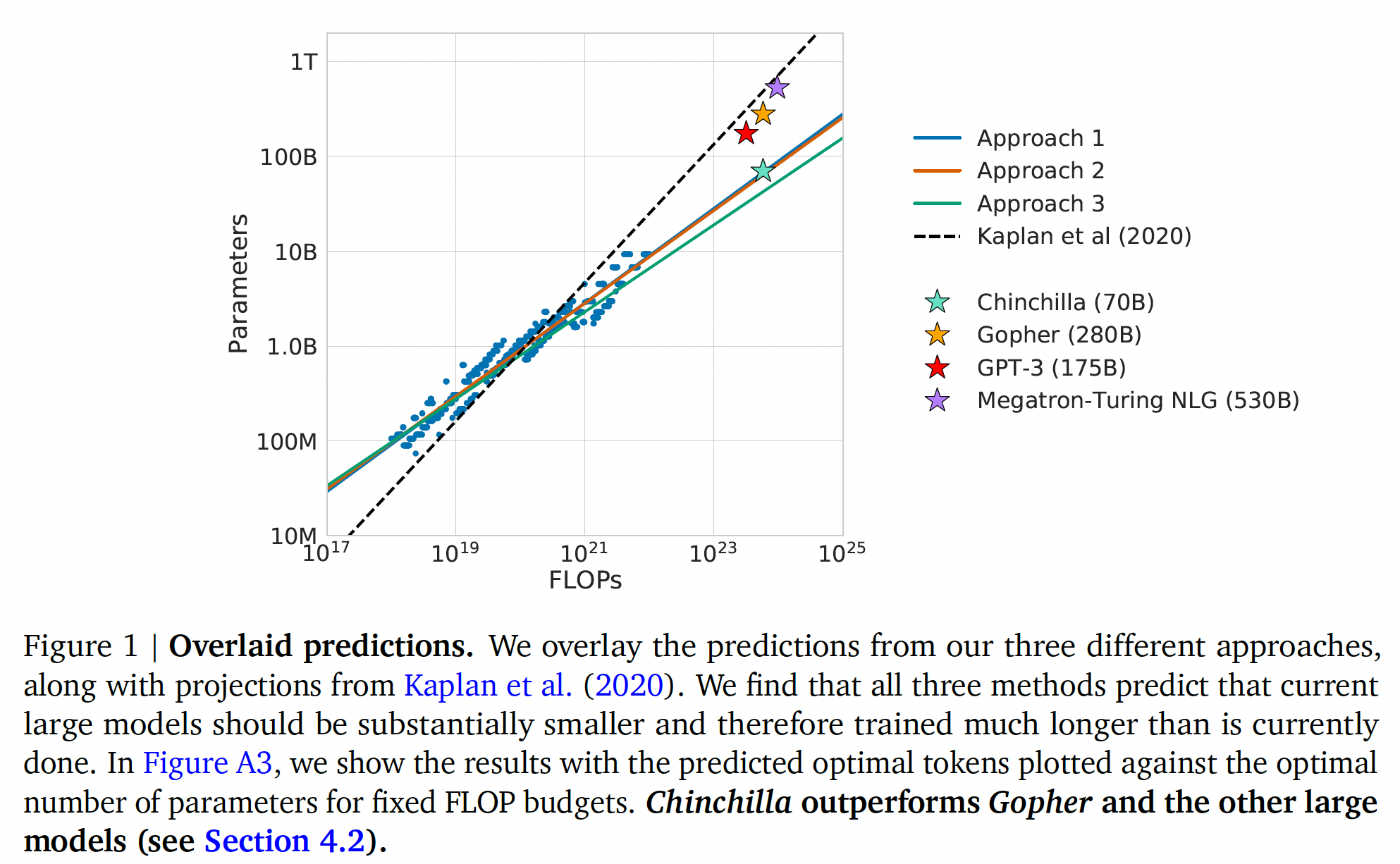
基于我们估计的
compute-optimal边界,我们预测,对于用于训练Gopher的compute budget,最优模型应该小4倍,同时在4倍的tokens上进行训练。我们通过在1.4T tokens上训练一个更加compute-optimal的70B模型,称为Chinchilla,来验证这一点。Chinchilla不仅比其更大的同类模型Gopher表现出色,而且其减少的模型尺寸大大降低了推理成本,并大大促进了下游在更小硬件上的使用。大型语言模型的能源成本通过inference和微调的使用而摊销。因此,一个经过优化训练的小型模型,其好处要超过改善模型性能的直接好处。相关工作:
大型语言模型:在过去的几年里,各种大型语言模型已经被引入。这些模型包括
dense transformer models、以及mixture-of-expert (MoE) models。最大的dense transformers已经超过500B参数(《Using Deepspeed and Megatron to Train Megatron-turing NLG 530b, A Large-Scale Generative Language Model》)。训练越来越大的模型的动力是很明显的:到目前为止,增加语言模型的规模已经在许多语言建模任务中提高了
SOTA。然而,大型语言模型面临着一些挑战,包括它们巨大的计算需求(training和inference的成本随着模型的大小而增加),以及需要获得更多的高质量训练数据。事实上,在这项工作中,我们发现更大的、高质量的数据集将在语言模型的任何further scaling中发挥关键作用。对
scaling行为进行建模:了解语言模型的scaling行为及其迁移特性(transfer property)在最近的大型模型的发展中一直很重要。《Scaling laws for neural language models》首次展示了模型大小与loss之间在许多数量级上的predictable relationship。作者研究了在给定的计算预算(compute budget)下选择最佳的模型大小来训练的问题。与我们类似,他们通过训练各种模型来解决这个问题。我们的工作在几个重要方面与《Scaling laws for neural language models》不同:首先,作者对所有的模型都使用了固定的
training tokens数量和学习率调度;这使得他们无法建模这些超参数对loss的影响。相比之下,我们发现,无论模型大小如何,将学习率调度设置为与training tokens数量大致匹配的结果是最好的final loss,如下图所示。《Scaling Laws for Neural Language Models》论文中并未固定training tokens数量,所以这里的结论是从何而来?上面三个子图:
training steps = 8M;下面三个子图:training steps = 12.5M。每条曲线分别代表余弦学习率的周期长度为training steps数量对于一个固定的
learning rate cosine schedule,从训练刚开始到130B tokens,中间的loss estimates(对于schedule length所训练的模型的loss。使用这些中间的loss的结果是,低估了在少于130B tokens的数据上训练模型的有效性,并最终促成了这样的结论:随着计算预算的增加,模型规模的增加应该快于训练数据规模。相反,我们的分析的预测表明,这两个数量应该以大致相同的速度scale。给定一个
training tokens数量,由于学习率调度的non-optimal选择,导致了训练得到的training loss要比最优的training loss更高。注意,这里是
training loss,而《Scaling Laws for Neural Language Models》中的指标是test loss。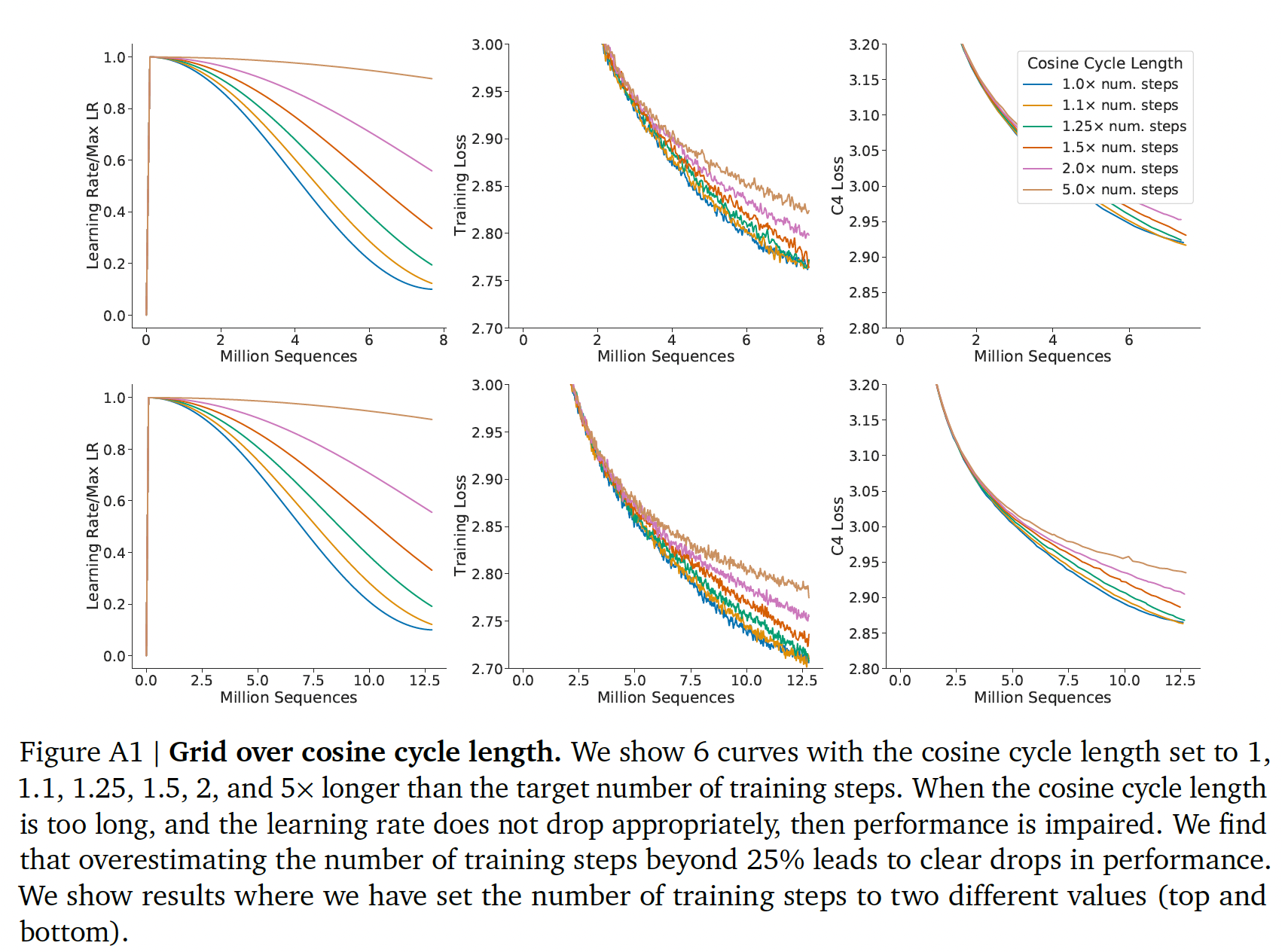
其次,我们包括参数高达
16B的模型,因为我们观察到FLOP-loss边界有轻微的曲率。这意味着来自非常小的模型的预测与来自较大模型的预测不同。事实上,我们分析中使用的大多数模型都有超过500M个参数。相比之下,《Scaling laws for neural language models》的大多数runs都要小得多,许多模型的参数不到100M。不同颜色的
training loss曲线代表了不同大小的模型。在下图中,我们显示了使用第一批三个
frontier-points、中间三个frontier-points、以及最后三个frontier-points的线性拟合(橙色虚线、绿色虚线、蓝色虚线)。在这项工作中,我们没有考虑到这一点,我们把它作为有趣的未来工作,因为它表明,对于大的FLOPs预算,甚至更小的模型也可能是最佳的。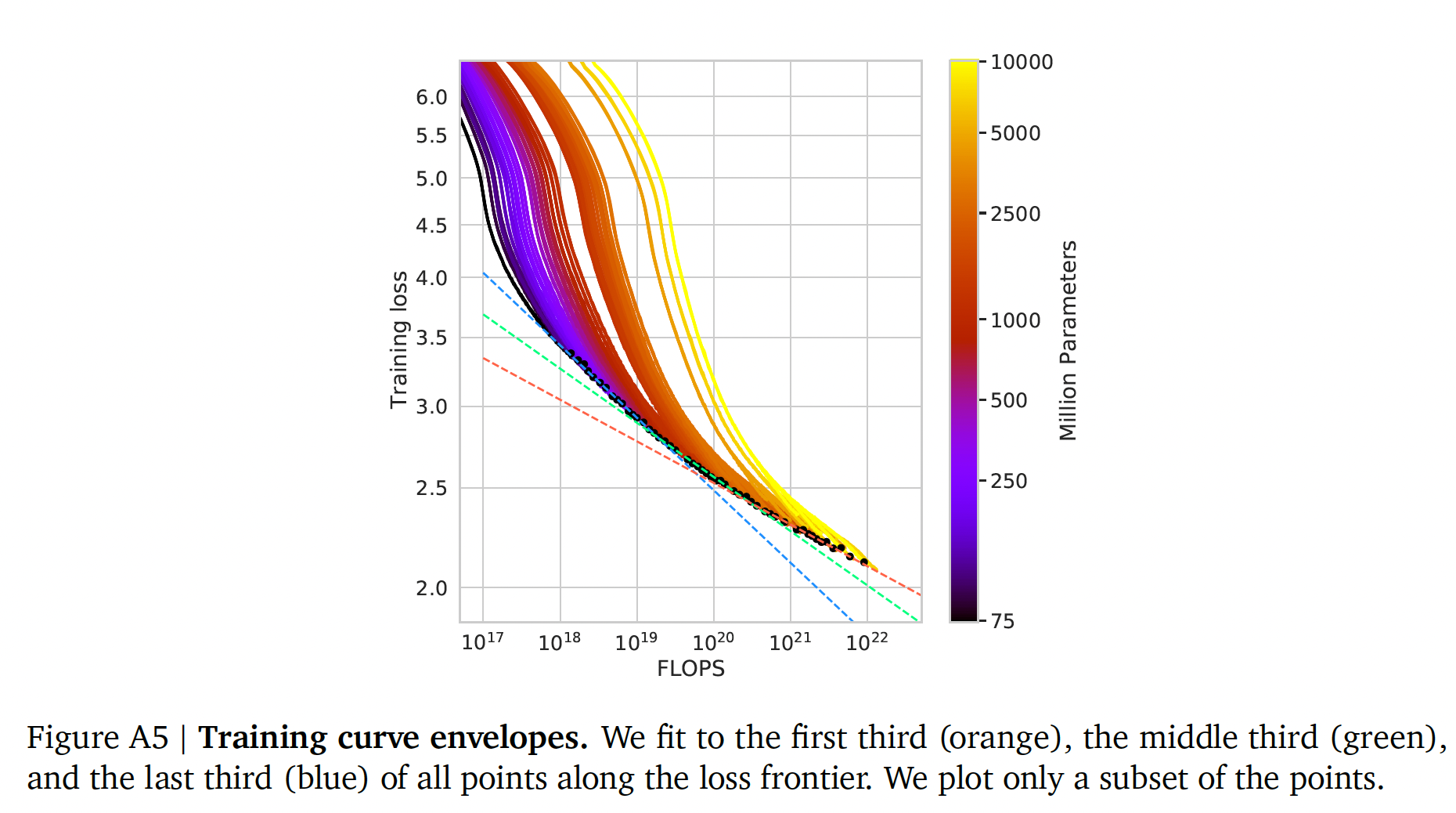
最近,
《Unified scaling laws for routed language models》专门研究了Mixture of Expert语言模型的scaling特性,表明随着模型规模的增加,expert数量的scaling会减弱。他们的方法将loss作为两个变量的函数:模型规模、专家数量。然而,与《Scaling laws for neural language models》一样,该分析是在固定数量的training tokens下进行的,有可能低估了branching的改进。为大型模型而估计超参数:在选择语言模型,并且选择训练模型的程序时,模型大小和
training tokens数量并不是唯一需要选择的两个超参数。其他重要的超参数包括学习率、学习率调度、batch size、优化器、宽深比(width-to-depth ratio)。在这项工作中,我们专注于模型大小和training steps数量,我们依靠现有的工作、以及所提供的实验启发式方法来确定其他必要的超参数。《Tuning large neural networks via zero-shot hyperparameter transfer》研究了如何选择这些超参数来训练自回归变transformer,包括学习率和batch size。《An empirical model of large-batch training》发现最佳batch size和模型大小之间只有微弱的依赖性。《Measuring the effects of data parallelism on neural network training》提出,使用比我们使用的更大的batch size是可能的。《The depth-to-width interplay in self-attention》研究了各种standard model size的最佳depth-to-width ratio。我们使用比所提议的深度稍小的模型,因为这可以在我们的硬件上转化为更好的wall-clock performance。
改进的模型架构:最近,人们提出了各种有前途的替代传统
dense transformer的方法。例如,通过使用条件计算, 大型MoE模型 (如1.7T参数的Switch transformer、1.2T参数的GLaM模型,以及其他模型)能够提供较大的有效model size,但是使用相对较少的training FLOPs和inference FLOPs。然而,对于非常大的模型,routed model的计算优势似乎在减少(《Unified scaling laws for routed language models》)。改进语言模型的一个正交方法是用明确的检索机制来
augment transformer。这种方法有效地增加了训练期间看到的tokens数量(在《Improving language models by retrieving from trillions of tokens》中增加了10倍)。这表明,语言模型的性能可能比以前认为的更加依赖于训练数据的大小。
44.1 方法
我们提出三种不同的方法来回答问题: 在固定的
FLOPs预算下,应该如何权衡模型大小和training tokens数量?在所有三种情况下,我们首先训练一系列模型,改变模型大小和training tokens数量,并使用所得的训练曲线来拟合一个empirical estimator,该empirical estimator关于应该如何scale。我们假设计算量和模型大小之间存在幂律关系,正如《Unified scaling laws for routed language models》、《Scaling laws for neural language models》所做的那样,尽管未来的工作可能希望针对大的模型规模在这种关系中包括潜在曲率(potential curvature)。所有三种方法的预测结果都是相似的,并且表明参数数量和
training tokens数量应该随着计算量的增加而同样增加,这个比例如下表所示(括号里的值分别是10%分位、90%分位的统计结果)。这与以前关于这个主题的工作形成了显著的对比,值得进一步研究。注意,
《Scaling laws for neural language models》研究的是test loss,而这里研究的是training loss。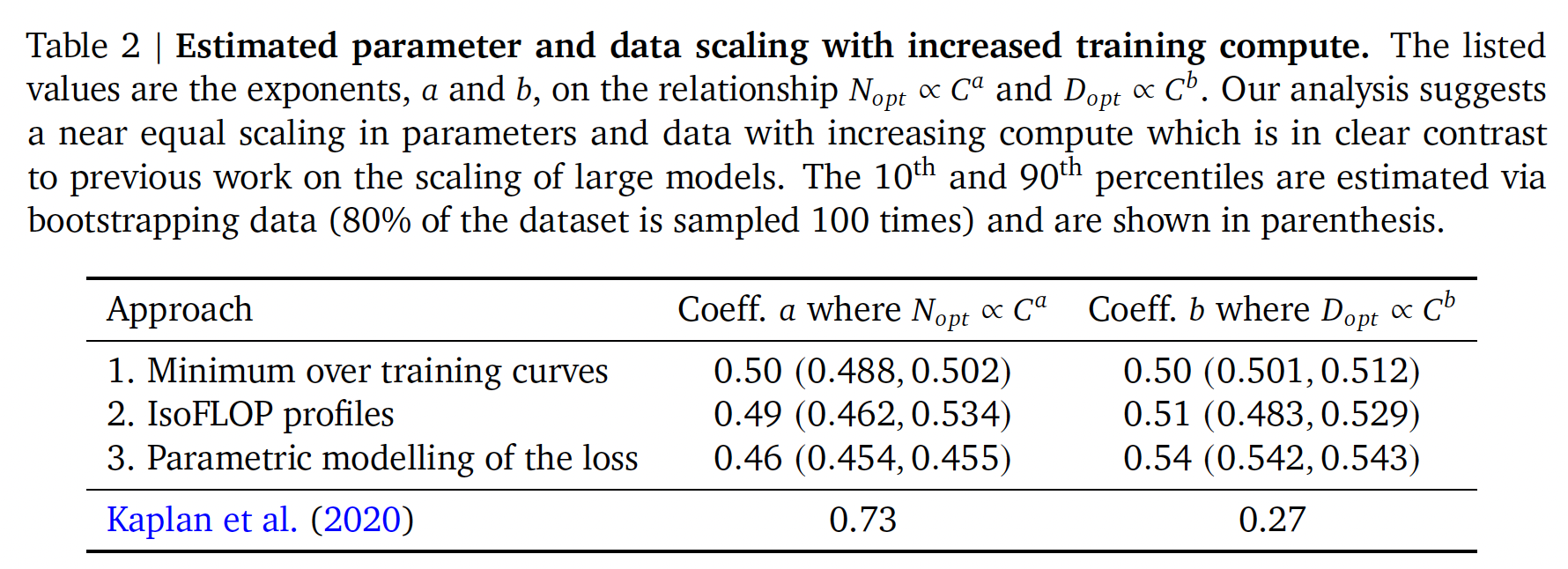
44.1.1 方法一:固定模型规模并改变 training tokens 数量
在我们的第一种方法中,我们针对一系列的固定规模的模型(模型参数从
70M到10B)改变训练步数,为每个模型训练4个不同数量的training sequences(即,training seen examples数量)。从这些runs中,我们能够直接提取在定数量的training FLOPs下实现的最小loss的估计。四个不同数量的
training sequences是如何实现的?如果是非常大的数据集,那么很可能最长的training steps都没能过遍历一个epoch,此时,每个样本仅被训练一次;如果是较小的数据,那么很可能最短的training steps都遍历了多个epoch,此时每个样本被训练多次。论文并未说明预训练的
datasets是如何构建的。我们对最小的模型使用最大的学习率为
10倍。我们假设余弦周期的长度应该与训练步数大致匹配。我们发现,当余弦周期长度超出训练步数25%以上时,性能会明显下降,如下图所示。 我们使用窗长为10步的高斯平滑来平滑训练曲线。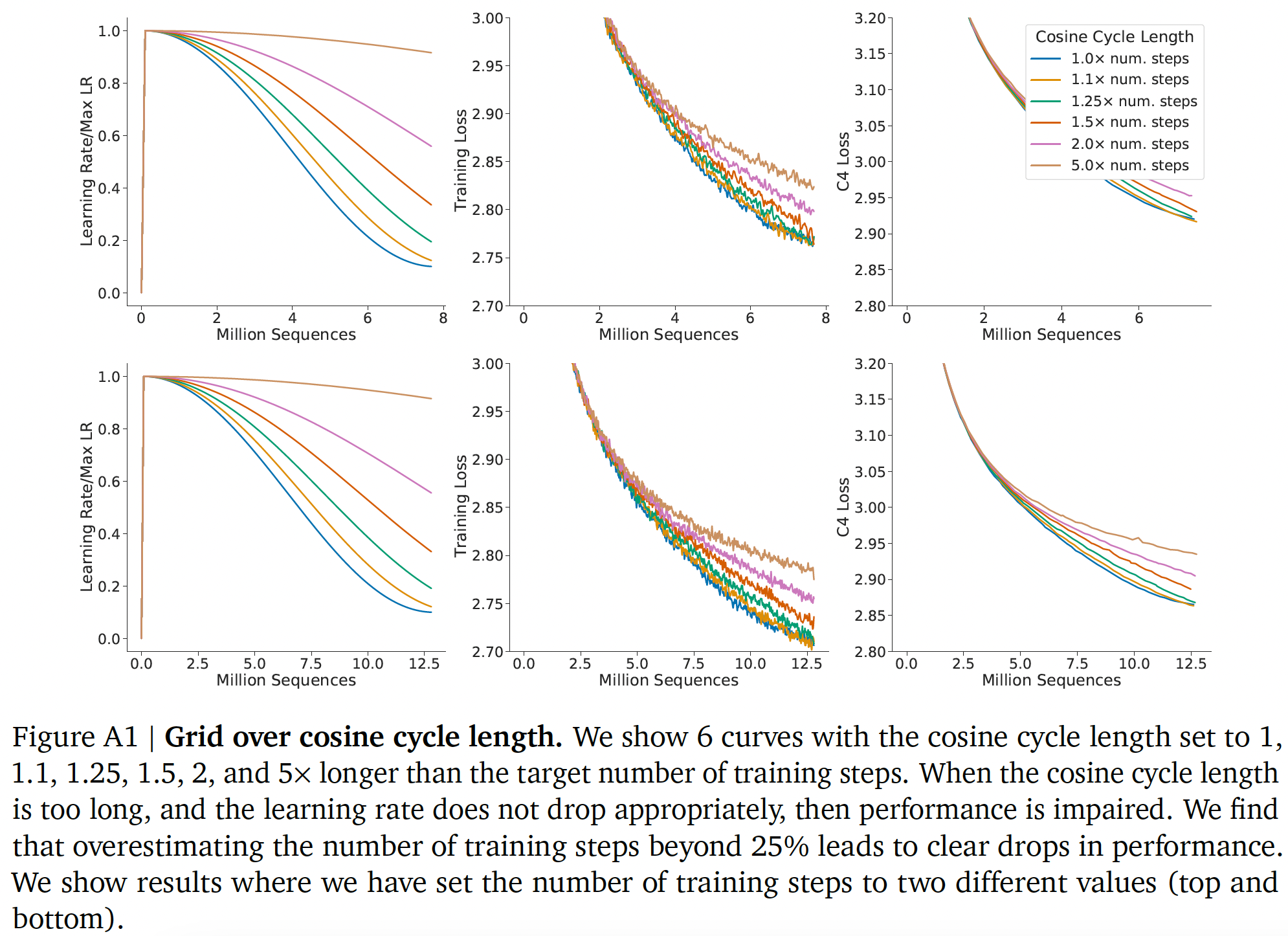
对于每个参数数量
4个不同的模型(因此一共训练了16x的horizon(以training tokens数量来衡量)上将学习率衰减10倍。然后,对于每次run,我们平滑并插值训练损失曲线。由此,我们得到一个从FLOP数量到training loss的连续映射(如下左图所示)。然后:对于每个
FLOP数量,我们确定哪个runs的loss最低(左图的灰色边界线)。是否存在这样的可能性:对于给定的
FLOP数量,有多个配置都能达到最低的training loss?即,是否存在使用这些插值,我们得到了从任何
FLOP数量most efficient choice的模型大小training tokens数量
在
1500个对数间隔的FLOP值中,我们找到哪个模型大小能实现所有模型的最低loss,以及所需的training tokens数量。最后,我们拟合幂律来估计任何给定计算量的最佳模型大小和training tokens数量,得到一个关系Table 2所总结的。在后续章节中,我们展示了在
FLOPs下的一对一比较,分别使用我们的分析所得到的模型规模、以及来自《Scaling laws for neural language models》的分析所得到的模型规模,使用我们预测的模型大小具有明显的优势。注意中间的图、右图中绿色直线给出了
Chinchilla的参数规模(67B)、FLOPs(Training Tokens(1.5T)。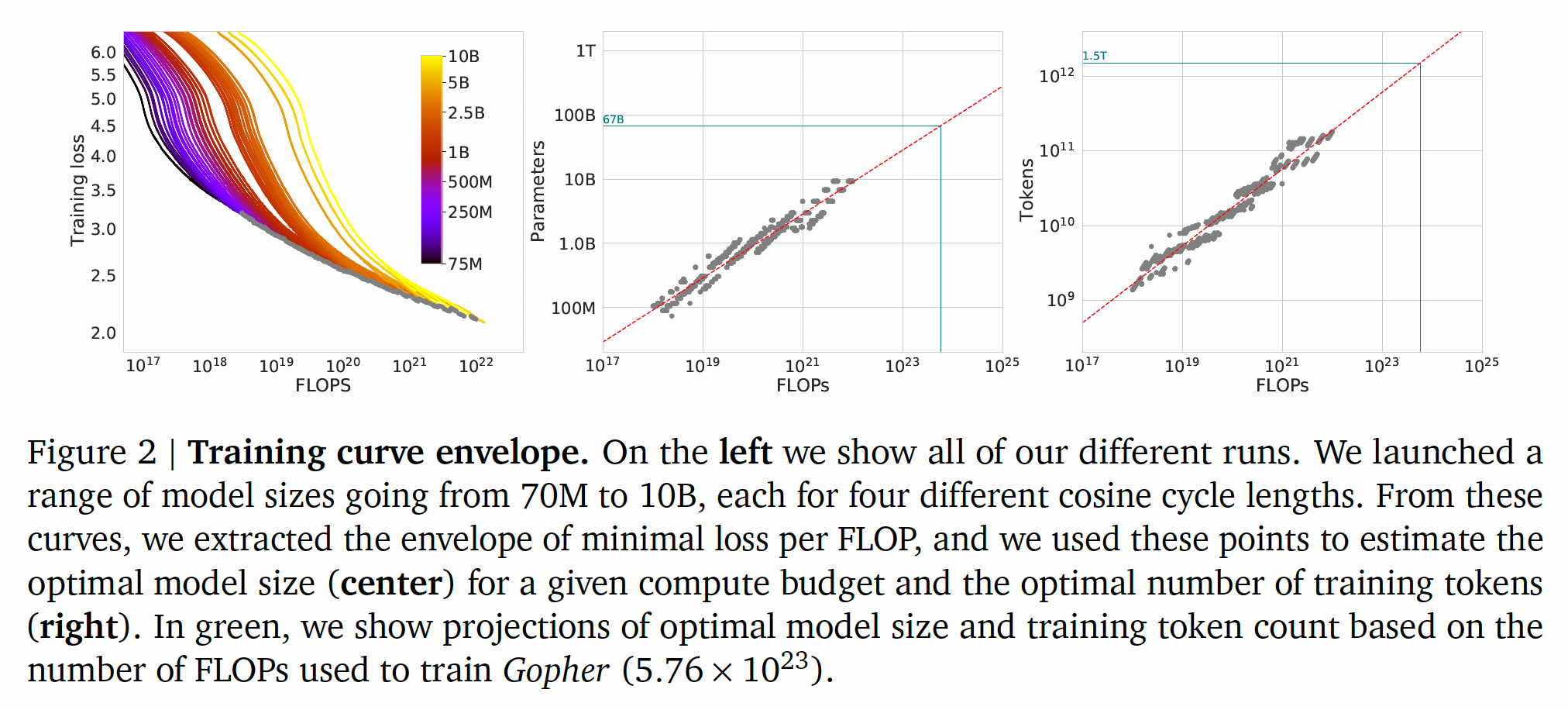
44.1.2 方法二:IsoFLOP profiles
在我们的第二个方法中,我们选择九种固定的
FLOP数量(从FLOPs),然后改变模型规模,然后考虑每种配置的final training loss。方法一需要沿着整个training runs考虑数据点(N, D, L)。与方法一相反,方法二允许我们直接回答问题:对于给定的FLOPs预算,最佳的参数规模是多少?方法二中,对应于给定
FLOPs数量的曲线中,Training Loss最小的点,横坐标就是最佳参数规模。对于每个
FLOP预算,我们在下图(左图)中绘制了final loss(平滑之后)与参数规模的对比。在所有情况下,我们确保我们已经训练了足够多样化的model size,以便在loss中看到一个明显的最小值。我们对每条IsoFLOPs曲线拟合一条抛物线,以直接估计在何种模型规模下达到最小loss。与方法一相同,我们随后在
FLOPs和loss-optimal的模型规模和training tokens数量之间拟合一个幂律,如下图的中间、右侧所示。再次,我们拟合指数函数的形式为Table 2所总结的。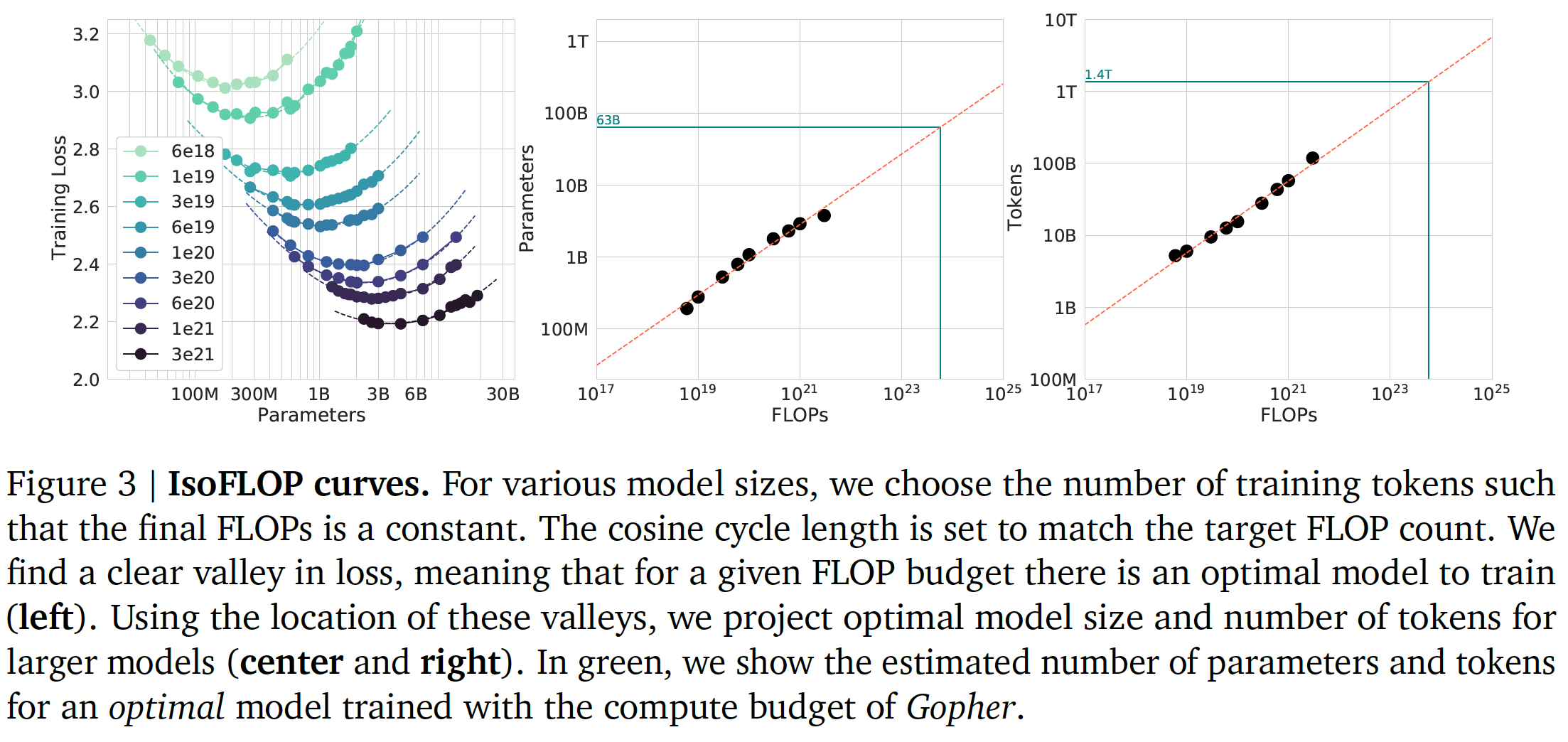
44.1.3 方法三:拟合损失函数
最后,我们将方法一和方法二中的实验的所有
final loss建模为模型参数数量training tokens数量D),我们提出以下函数形式:其中:
第一项捕获数据分布上的理想
generative process的损失,并应与自然文本的熵相对应。第二项反映了这样一个事实,即一个具有
perfectly trained transformer低于理想generative process的表现。模型规模越大,则模型拟合能力越强,因此
training loss越小。最后一项反映了一个事实,即
transformer没有被训练到收敛,因为我们只在数据集分布的一个样本(即,单个数据集)上进行了有限数量的optimisation steps。training tokens数量越大,则模型见过的样本越多,则training loss越小。
模型拟合:为了估计
L-BFGS算法,使predicted logloss和observed log loss之间的Huber loss最小:我们通过
a grid of initializations中选择最佳拟合从而来考虑可能的局部最小值。Huber loss(其中outliers是鲁棒的,我们发现这对held-out data points的良好预测性能很重要。原始论文的附录D详细介绍了拟合过程和loss decomposition。我们使用
较大的
更小的
resulting prediction。
有效的边界(
frontier):我们可以通过在约束条件parametric loss根据
《Scaling Laws for Neural Language Models》的推导过程,根据公式的结构,它们具有幂律形式:
这是怎么推导来的?论文并未详细说明。
我们在下图(左图)中显示了被拟合的函数
efficient computational frontier。通过这种方法,我们发现Table 2所总结的。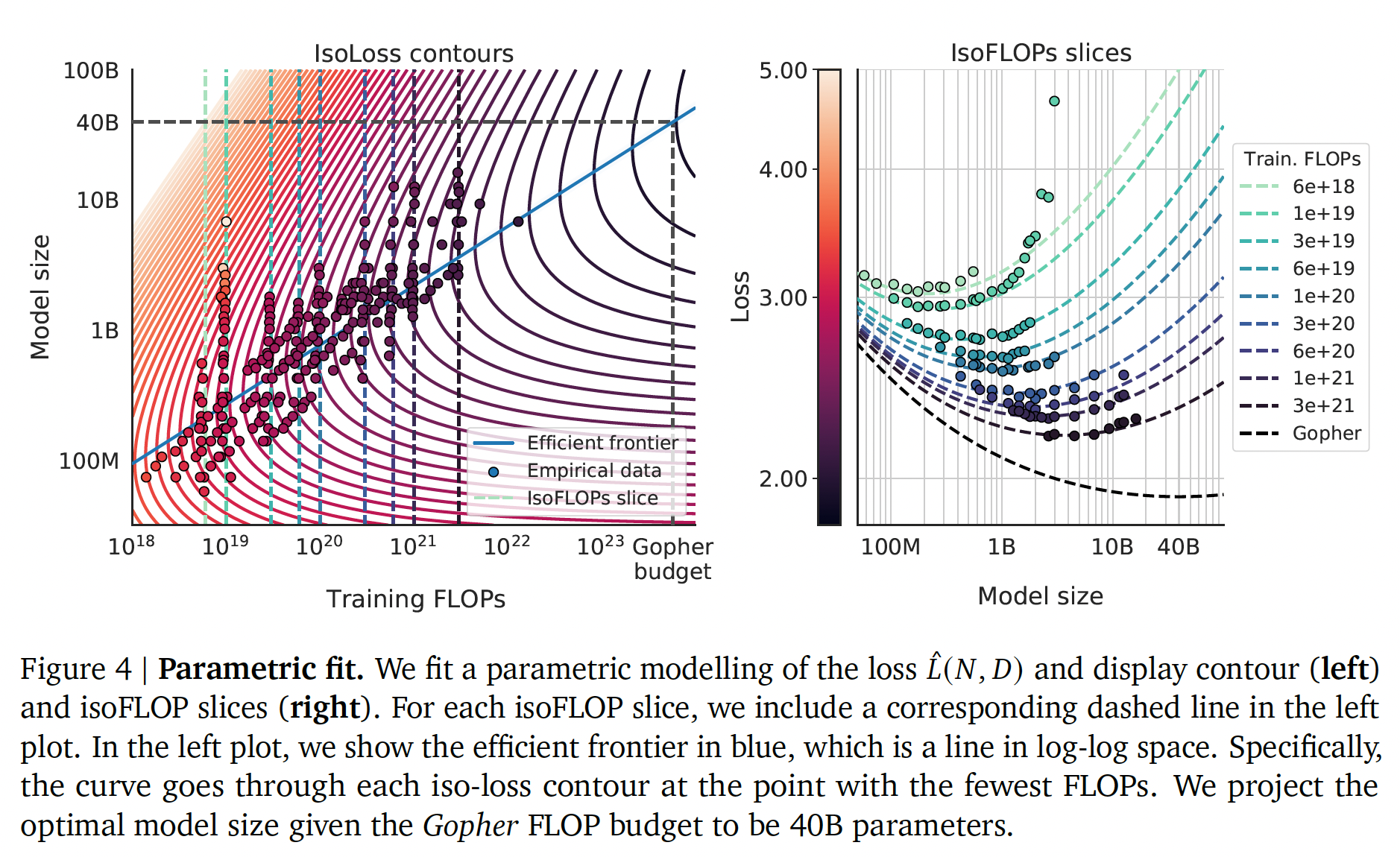
44.1.4 最优的 model scaling
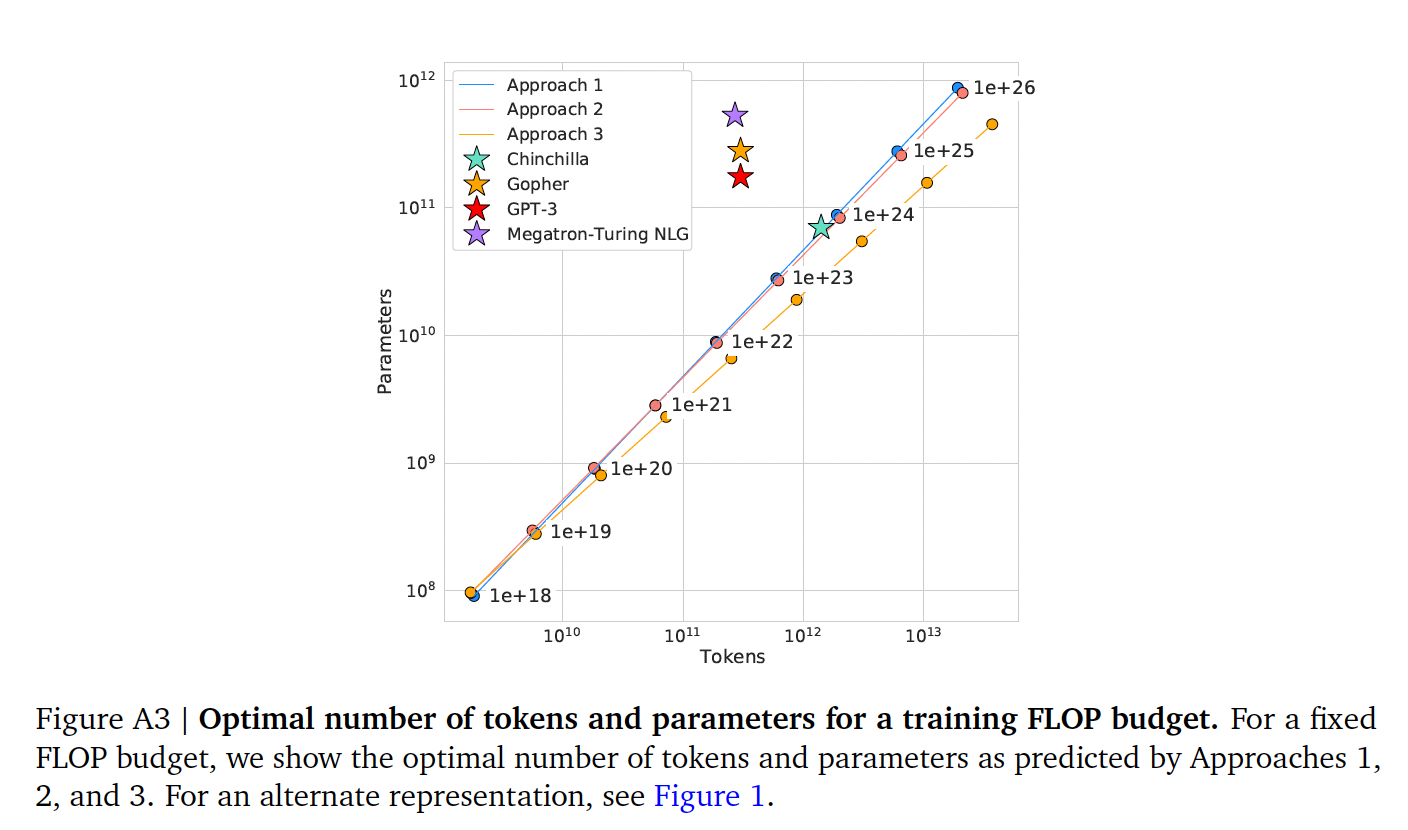
我们发现,尽管使用了不同的拟合方法和不同的
trained model,在parameters和tokens方面,针对最佳scaling产生了comparable predictions(如Table 2所示)。所有三种方法都表明,随着计算预算的增加,模型的规模和训练数据的数量应该以大致相等的比例增加。如
Figure 1和Figure A3所示,第一方法和第二种方法对最佳模型大小的预测非常相似。第三种方法预测,在较大的计算预算下,更小的模型是最佳的。
我们注意到,低的
training FLOPs(observed pointspoints,具有更大的残差FLOPs的点上:由于Huber loss,自动地将低计算预算的点视为outliers。作为经验上观察到的边界Figure A5),这导致预测的



在下表中,我们显示了在
compute-optimal frontier上,给定大小的模型所对应的预估FLOPs数量和token数量。们的发现表明,考虑到它们各自的计算预算,目前这一代的大型语言模型的规模明显过大,如Figure 1所示。例如:我们发现一个175B参数的模型应该用FLOPs的计算预算、以及超过4.2T tokens进行训练。4.41, 4.2, 6.8等等,这几个数值在下面的表格中找不到,原因有两个:首先,表格中给出的是方法一的估计值,而作者并没有说这几个数值是通过方法一还是方法二/三估计而来;其次,表格中给出的参数与这里正文部分描述的参数有一定的差距,这导致了结果上的差异。在计算预算约为
FLOPs的情况下,一个280B的Gopher-like模型是最佳的训练模型,应该在6.8T tokens上训练。除非有FLOPs的计算预算(超过了250倍的用于训练Gopher的计算量),否则1T参数的模型不太可能是optimal model从而用于训练 。此外,预计需要的训练数据量远远超过了目前用于训练大型模型的数据量,并强调了除了允许model scale的engineering improvement之外,数据集收集的重要性。虽然推断出许多数量级有很大的不确定性,但我们的分析清楚地表明,鉴于目前许多
LLM的training compute budget,应该使用更小的模型在更多的token上进行训练,以实现最有效的模型。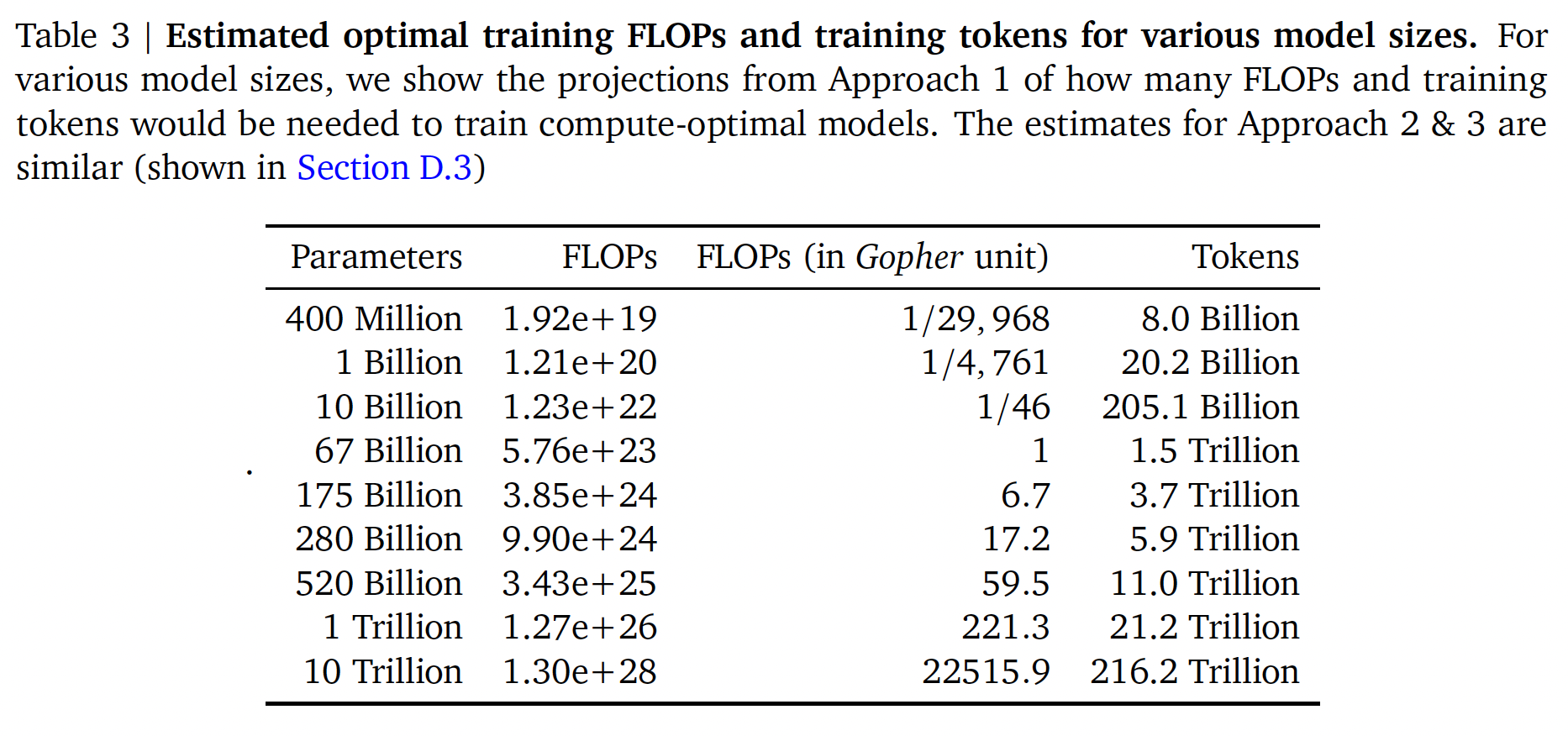
跨数据集的
scaling result的一致性:我们展示了在两个不同的数据集(C4和GitHub code)上训练之后的IsoFLOP(方法二)分析的scaling result。对于这两组使用MassiveText子集的实验,我们使用与MassiveText实验相同的tokenizer。MassiveText数据集是Gopher预训练所用的数据集,也是Chinchilla所用的预训练数据集。如下图和下表所示,在这两种情况下,我们都得出了类似的结论,即模型大小和
training tokens数量应该以相等的比例进行缩放。这表明我们的结果是独立于数据集的,只要不进行超过一个epoch的训练。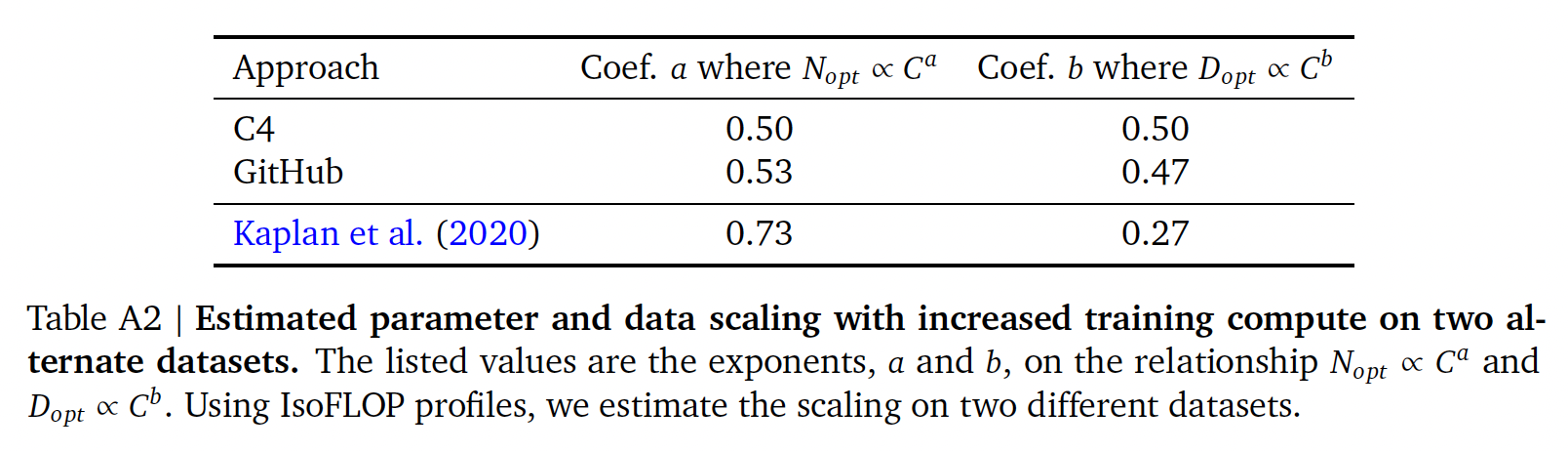
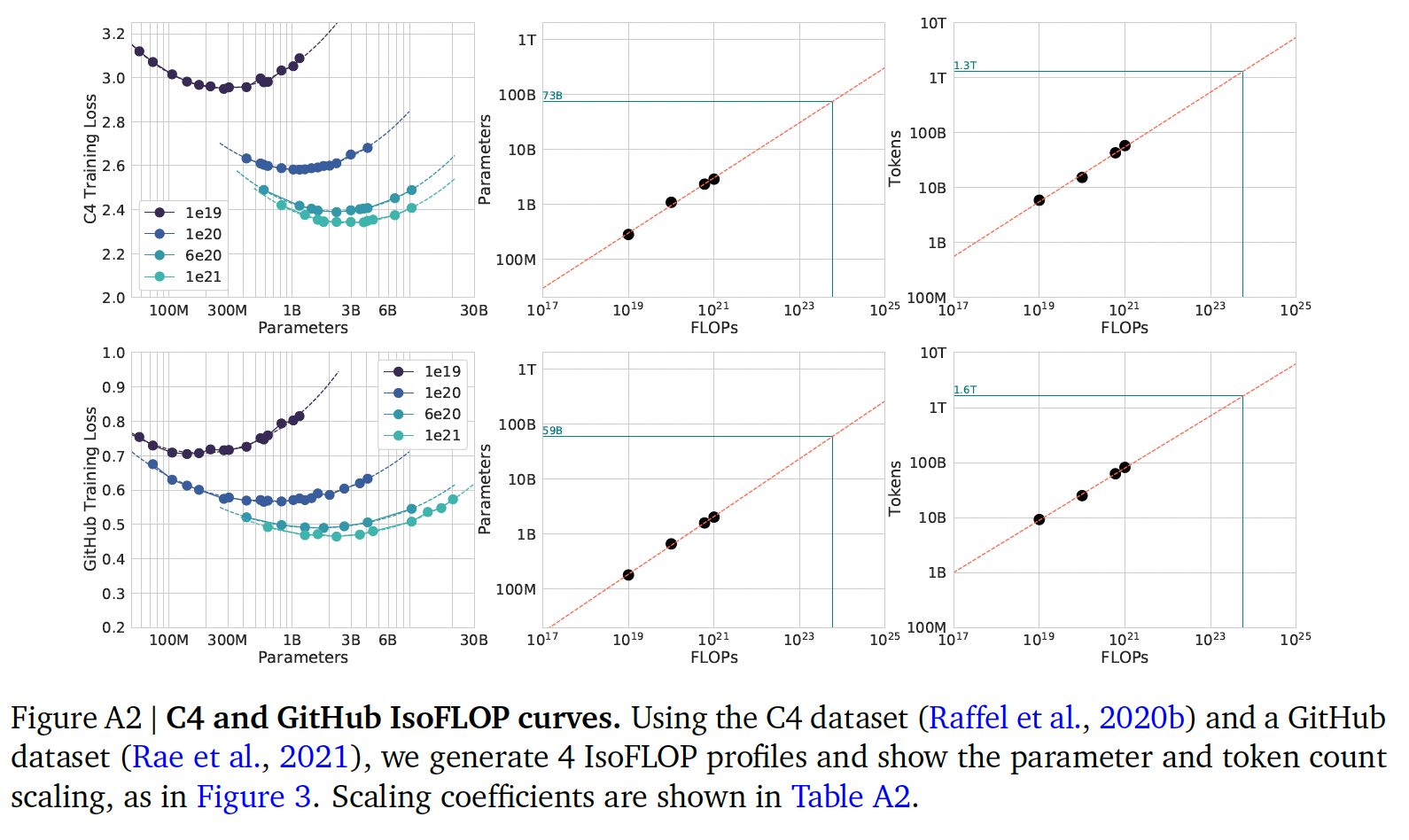
对于方法二和方法三,我们在下表中展示了各种计算预算下的估计模型大小和
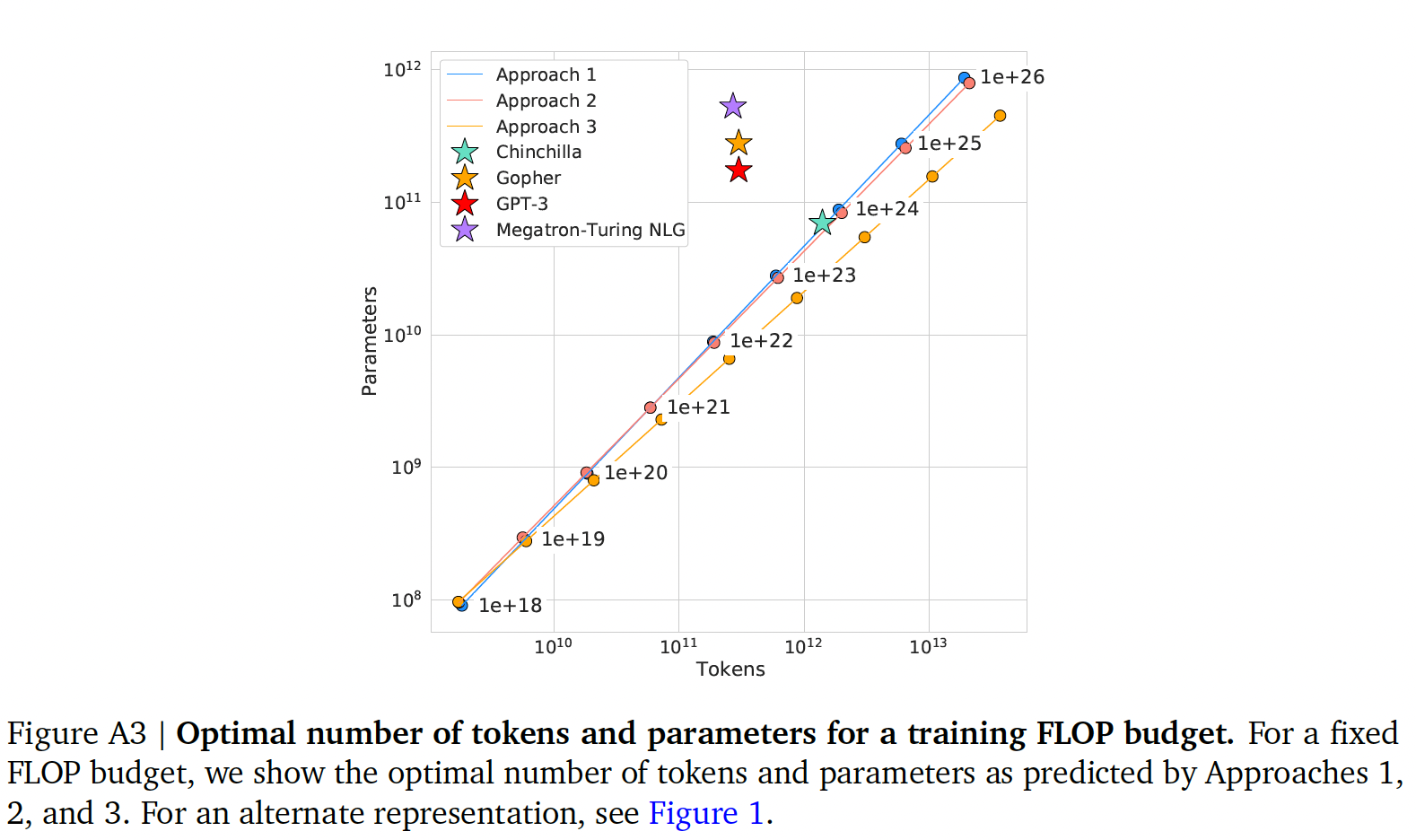
training tokens数量。我们在下图中绘制了三种方法在各种FLOPs预算下预测的tokens数量和参数数量。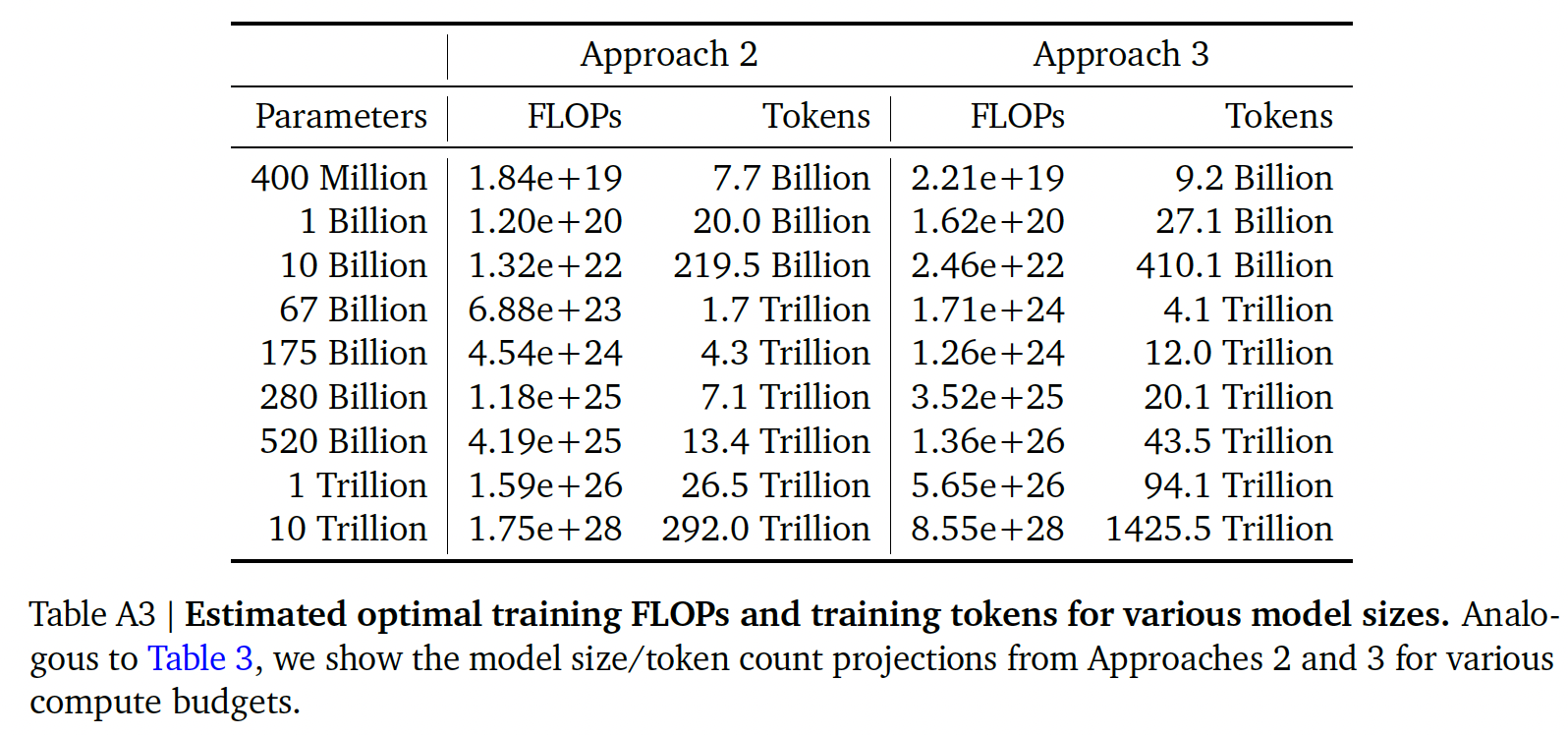
44.2 Chinchilla
根据我们前面的分析,
Gopher计算预算的最佳模型大小是在40B到70B参数之间。出于数据集和计算效率的考虑,我们在这个范围的较大一侧(即,70B参数)训练了一个模型,traing tokens数量为1.4T,从而用来验证这个假设。在本节中,我们将这个模型(我们称之为Chinchilla)与Gopher和其他大型语言模型进行比较。Chinchilla和Gopher都经过了相同数量的FLOPs来训练,但在模型的大小和training tokens数量上有所不同。虽然预训练一个大型语言模型有相当大的计算成本,但下游的微调和推理也构成了大量的计算用量。由于比
Gopher小4倍,Chinchilla的内存占用和推理成本也更小。
44.2.1 模型和训练细节
用于训练
Chinchilla的全部超参数在下表(Table 4)中给出。Chinchilla使用与Gopher相同的模型结构和训练设置,但下面列出的差异除外。我们在
MassiveText(与Gopher相同的数据集)上训练Chinchilla,但使用了稍微不同的子集分布(如下表所示),从而考虑到training tokens数量的增加。请注意,MassiveWeb和Wikipedia的子集都被用于一个以上的epoch(分别为1.24个epoch和3.4个epoch)。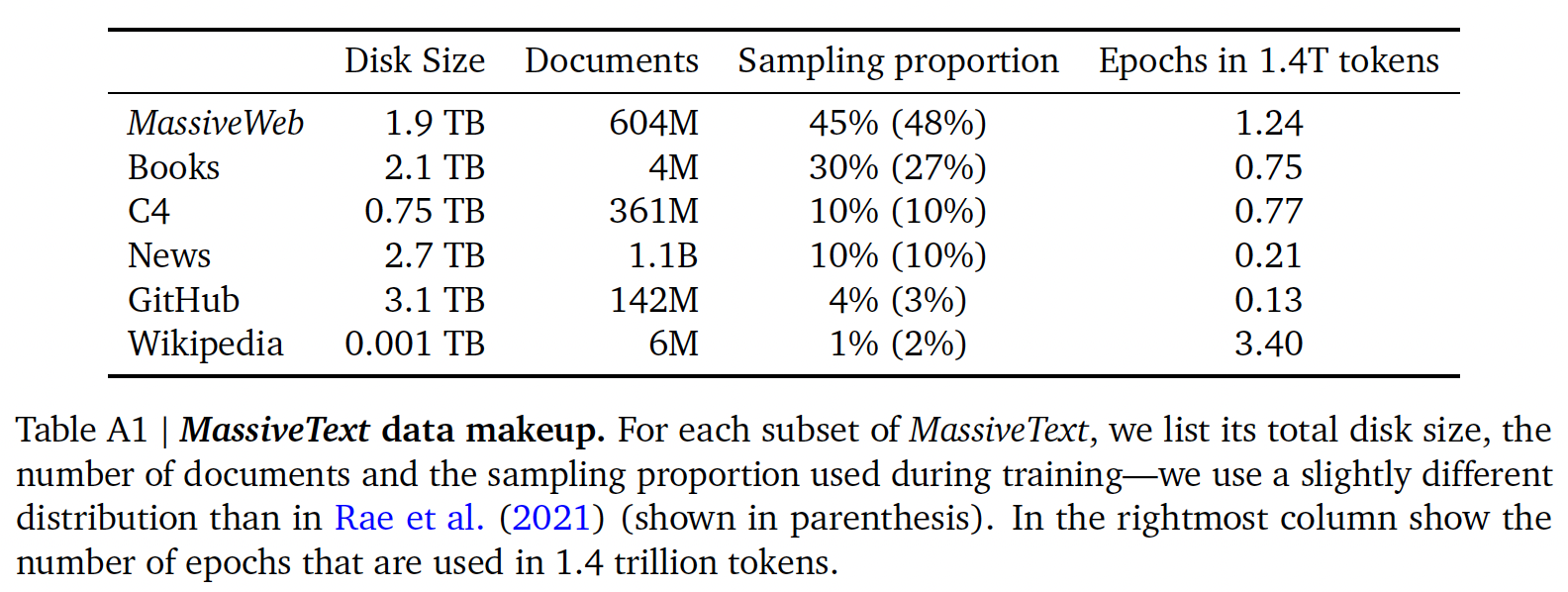
我们对
Chinchilla使用AdamW而不是Adam,因为这改善了language modelling loss和微调后的下游任务性能。我们用稍加修改的
SentencePiece tokenizer来训练Chinchilla,这个tokenizer不应用NFKC normalization。词表非常相似:94.15%的tokens与用于训练Gopher的tokens相同。例如,我们发现,这对数学和化学的representation特别有帮助。虽然前向传播和反向传播是以
bfloat16计算的,但我们在distributed optimizer state中存储了一份float32的权重。更多细节见《Scaling language models: Methods, analysis& insights from training Gopher》。
本分析中的所有模型都是在
TPUv3/TPUv4上用JAX和Haiku进行训练。原始论文附录A8中包括一张Chinchilla model card。
Chinchilla和Gopher的其它差异:除了模型大小和training tokens数量的差异,Chinchilla和Gopher之间还有一些额外的微小差异。具体来说,Gopher是用Adam训练的,而Chinchilla是用AdamW训练。此外,如前所述,Chinchilla在sharded optimiser state中存储了一份精度更高的权重。我们在下图
A6和A7中分别展示了用Adam和AdamW训练的模型的比较。我们发现,AdamW训练的模型比用Adam训练的模型要好,与学习率调度无关。图
A6:我们展示了一个680M参数的模型的比较,该模型是在使用和不使用更高精度的权重副本的情况下训练出来的,并且使用Adam/AdamW进行比较。橙色为Chinchilla、绿色为Gopher。图
A7:417M模型(蓝色)和1.4B模型(绿色),分别在AdamW优化器(虚线) 和Adam优化器(实线)下的比较。可以看到AdamW效果更好。

44.2.2 结果
我们对
Chinchilla进行了广泛的评估,与各种大型语言模型进行了比较。我们对Gopher提出的任务的一个大子集进行了评估,如下表所示。由于这项工作的重点是优化model scaling,我们包括了一个大型的代表性子集,并引入了一些新的评估,以便与其他现有的大型模型进行更好的比较。所有任务的评估细节与Gopher中描述的相同。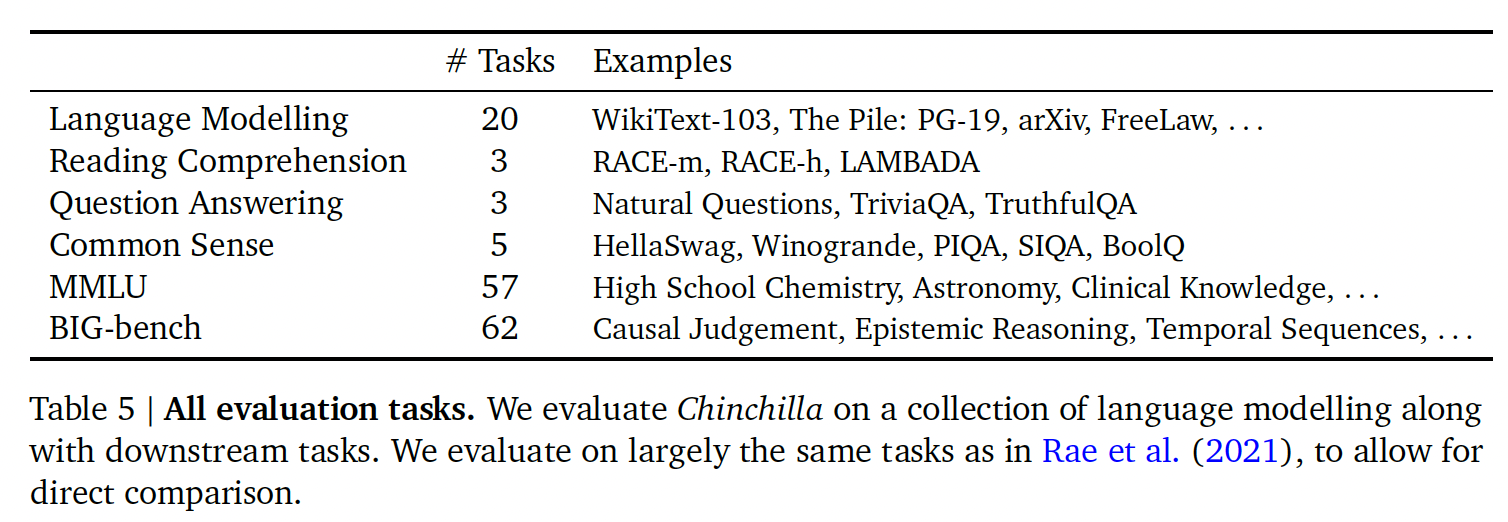
Language modelling:如下图所示:Chinchilla在The Pile的所有evaluation子集上都明显优于Gopher。与Jurassic-1(178B)相比,除了两个子集(dm_mathematics和ubuntu_irc),Chinchilla在所有子集上的性能更强。原始比较结果参考原始论文的Table A5。在
Wikitext103上,Chinchilla实现了7.16的困惑度,而Gopher为7.75。
在这些语言建模
benchmark上对Chinchilla和Gopher进行比较时需要谨慎,因为Chinchilla比Gopher多训练了4倍数据,因此训练集/测试集泄漏可能会人为地提高结果。因此,我们更强调其他的任务(如MMLU、BIG-bench、以及各种闭卷问答和常识分析),对于这些任务来说,泄漏是不那么令人担忧的。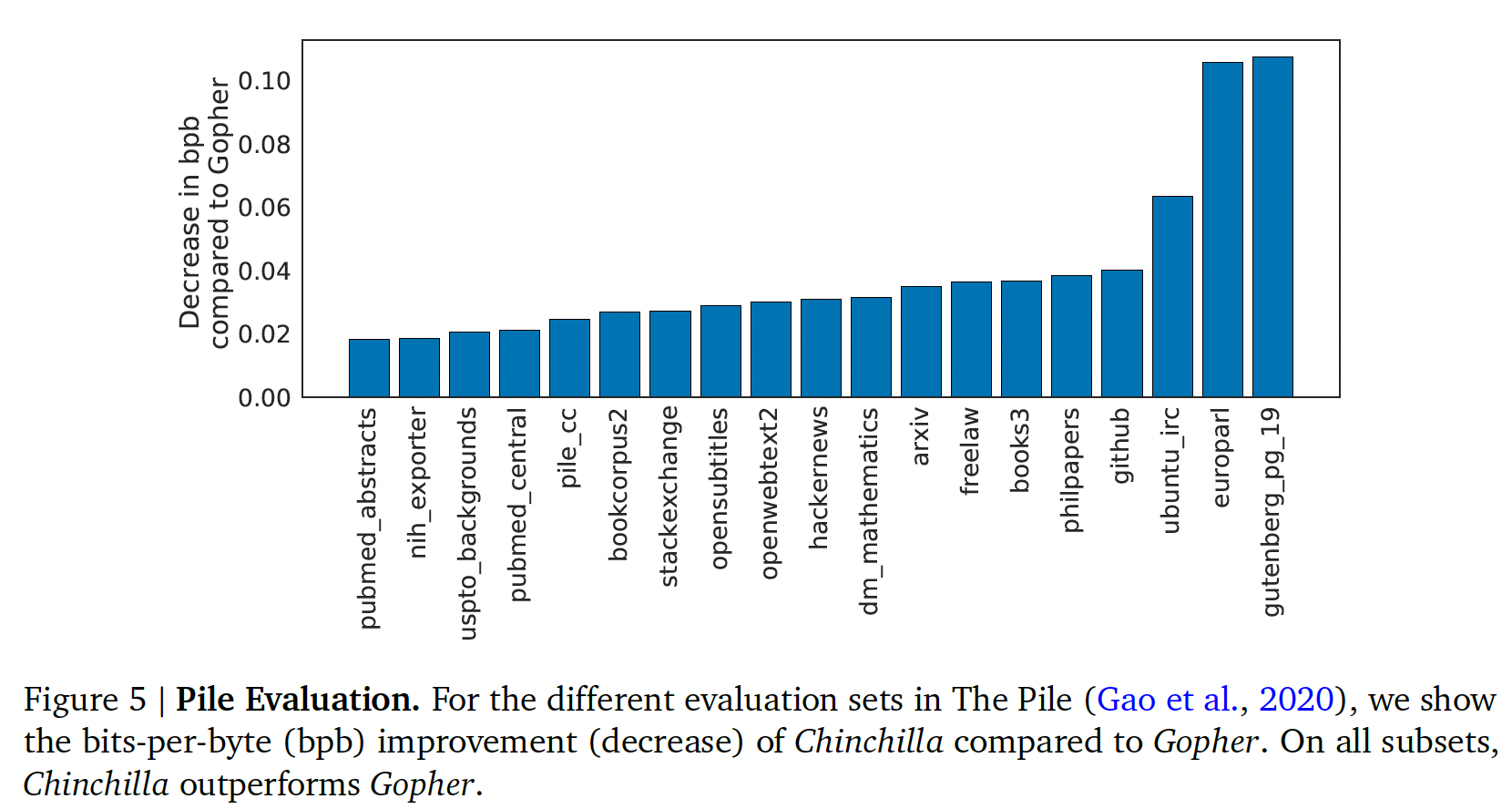
MMLU:大规模多任务语言理解(Massive Multitask Language Understanding: MMLU)benchmark包括一系列类似考试的学术科目上的问题。在下表中,我们报告了Chinchilla在MMLU上的平均5-shot成绩。详细结果参考原始论文A6。在这个
benchmark上,尽管Chinchilla小得多,但它的表现明显优于Gopher,其平均准确率为67.6%(比Gopher提高了7.6%)。值得注意的是,Chinchilla甚至超过了专家对June 2023 Forecast的63.4%准确率。此外,Chinchilla在4个不同的单独任务(高中政治、国际法、社会学和美国外交政策)上达到了90%以上的准确率。据我们所知,没有其他模型在一个子集上达到大于90%的准确率。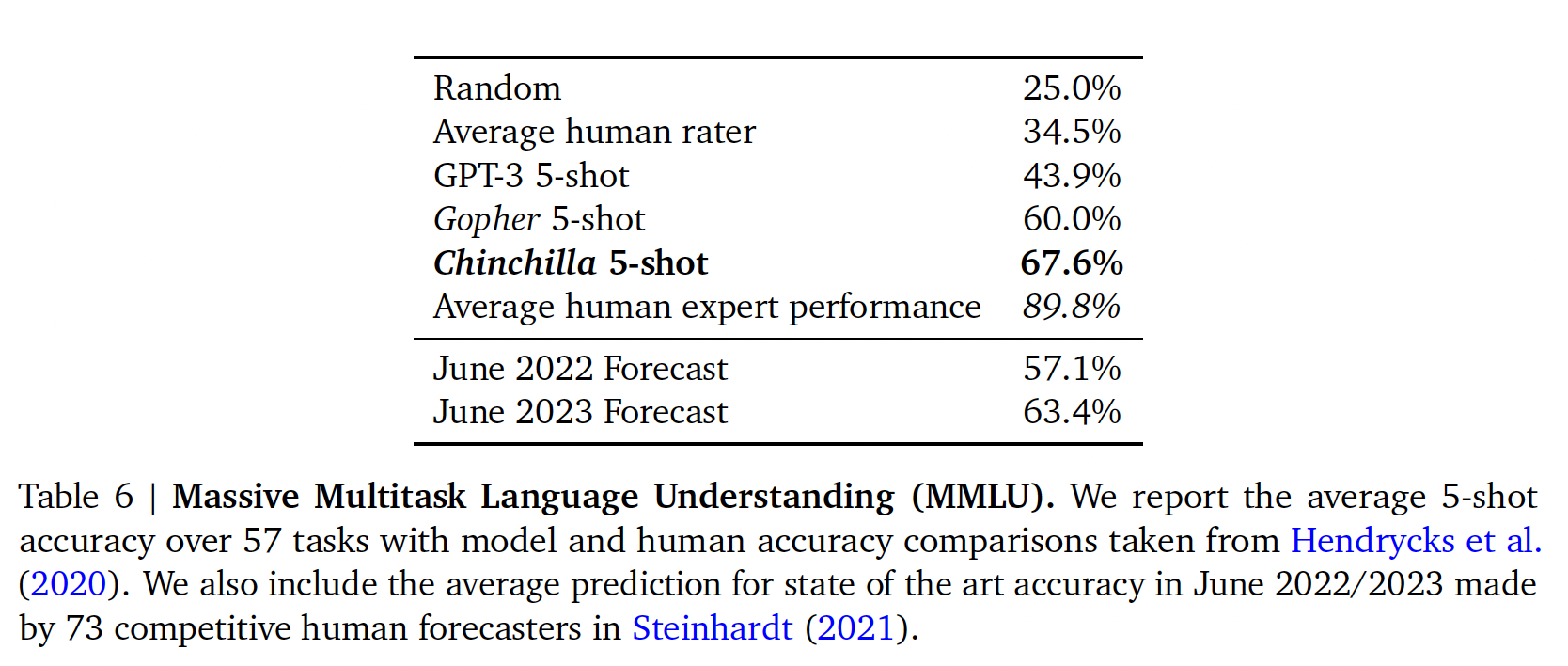
在下图中,我们展示了与
Gopher的比较,按任务划分。总的来说,我们发现Chinchilla在绝大多数的任务中都提高了性能。在四个任务(大学数学、计量经济学、道德情景、形式逻辑)中,Chinchilla的表现不如Gopher,而在另外两个任务中的表现没有变化。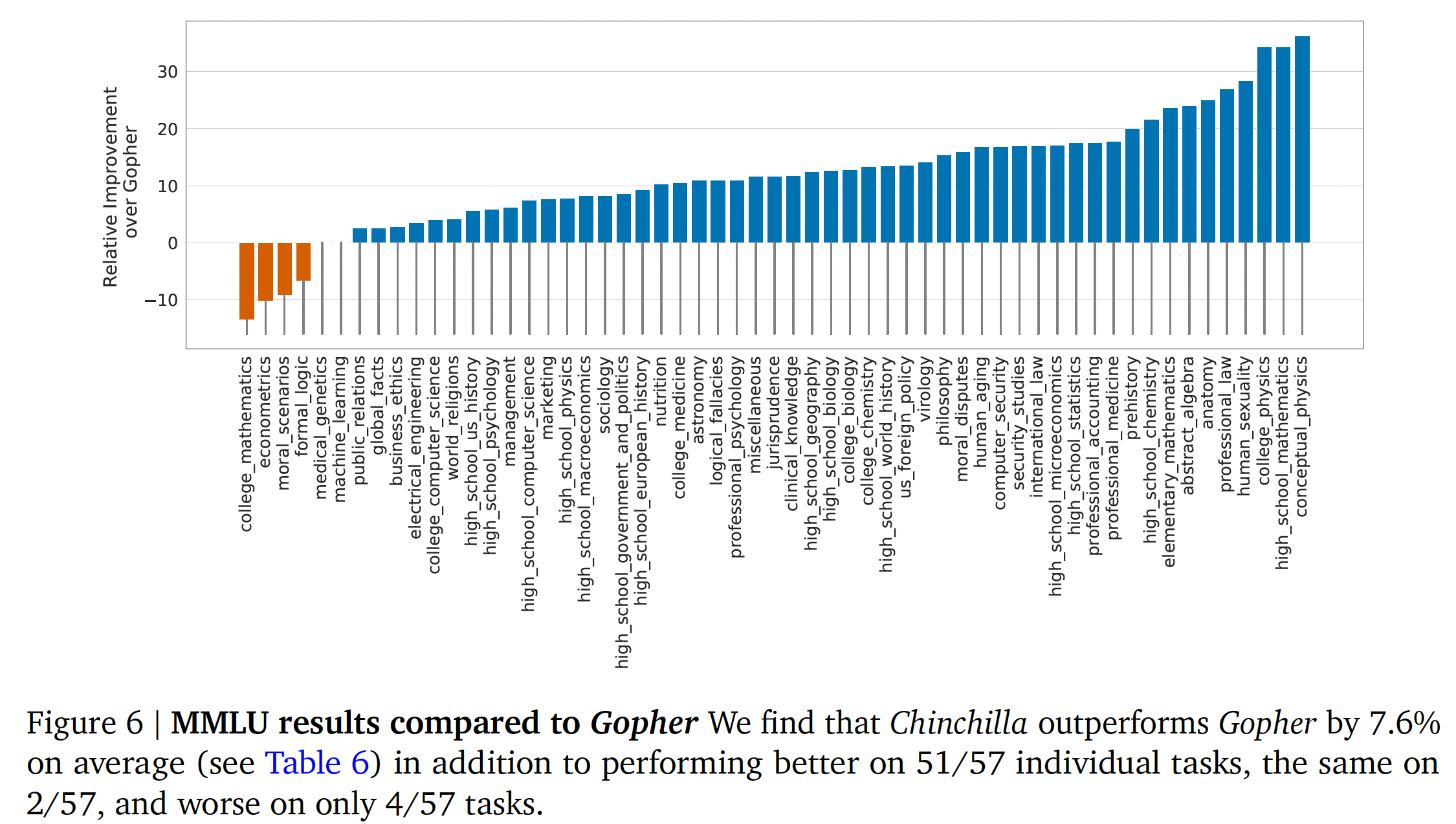
阅读理解:在
final word prediction数据集LAMBADA上,Chinchilla达到了77.4%的准确率,而Gopher的准确率为74.5%,MT-NLG 530B为76.6%(如下表所示)。在RACE-h和RACE-m上,Chinchilla的表现大大超过了Gopher,在这两种情况下,准确率提高了10%以上。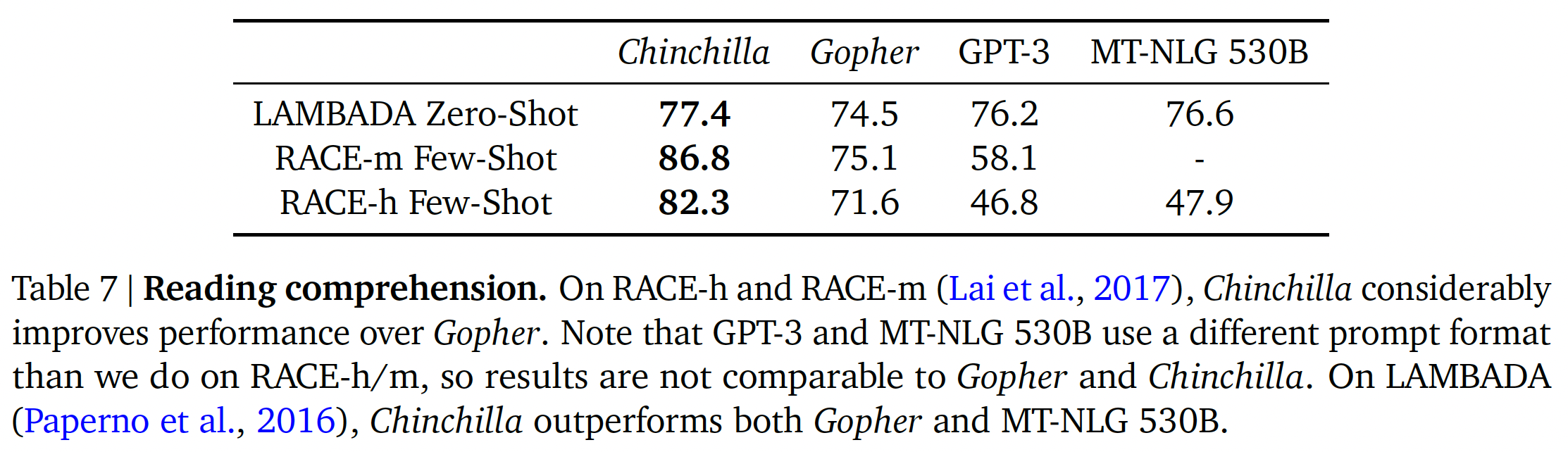
BIG-bench:我们在《Scaling language models: Methods, analysis& insights from training Gopher》报告的同一组BIG-bench任务上分析了Chinchilla。与我们在MMLU中观察到的情况类似,Chinchilla在绝大多数任务中都优于Gopher(如下图所示)。我们发现,Chinchilla将平均性能提高了10.7%,达到了65.1%的准确率,而Gopher则为54.4%。在我们考虑的62个任务中,Chinchilla只在四个任务上比Gopher表现得差:crash_blossom, dark_humor_detection,mathematical_induction, logical_args。Chinchilla的全部accuracy结果可以在原始论文的Table A7中找到。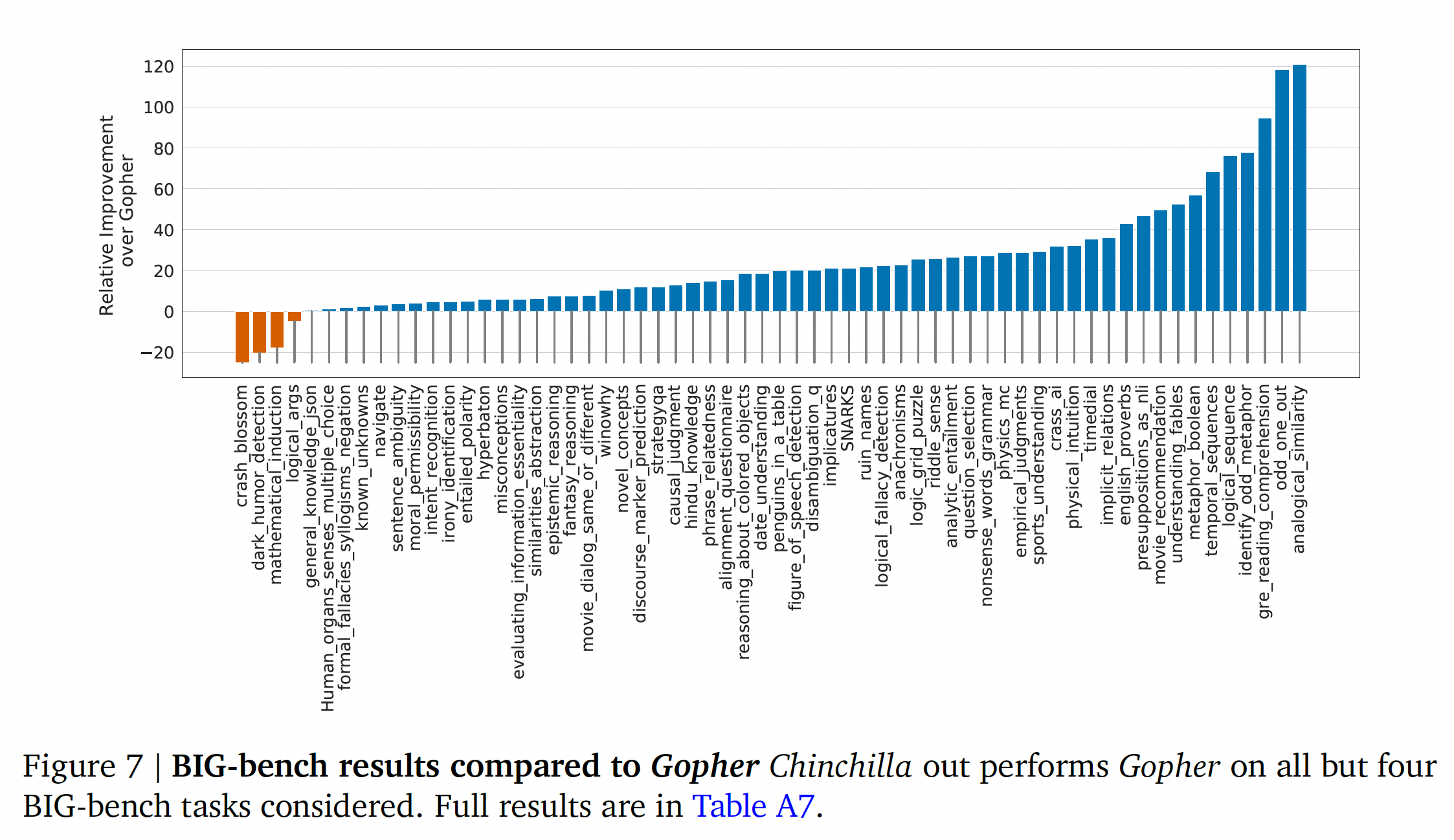
Common sense:我们在各种common sense benchmark上评估Chinchilla:PIQA、SIQA、Winogrande、HellaSwag和BoolQ。我们发现Chinchilla在所有任务上都优于Gopher和GPT-3,在除了一项任务之外的所有任务上都优于MT-NLG 530B,如下表所示。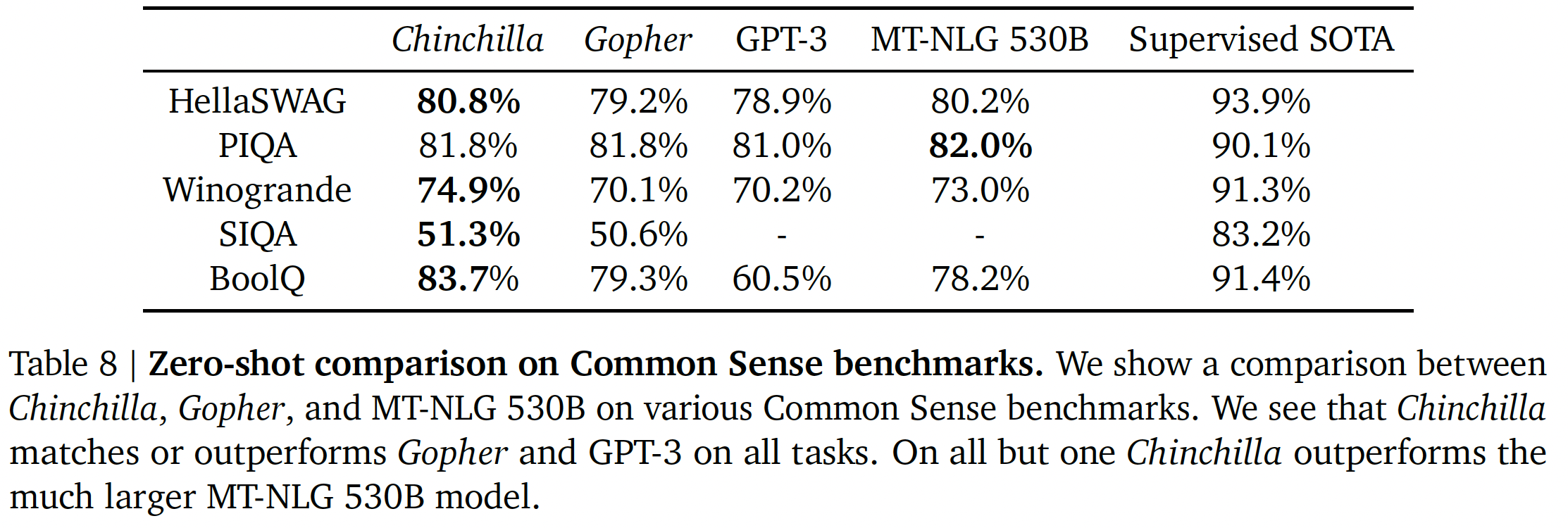
在
TruthfulQA上,Chinchilla在0-shot/5-shot/10-shot的情况下分别达到43.6%/58.5%/66.7%的准确率。相比之下,Gopher只达到了29.5%的0-shot、43.7%的10-shot准确率。与TruthfulQA的研究结果形成鲜明对比的是,Chinchilla取得的巨大改进(0-shot准确率的提升为14.1%)表明,仅对pre-training data进行更好的建模,就能在这个benchmark上取得实质性的改进。闭卷问答:下表中报告了闭卷问答
benchmark的结果。在
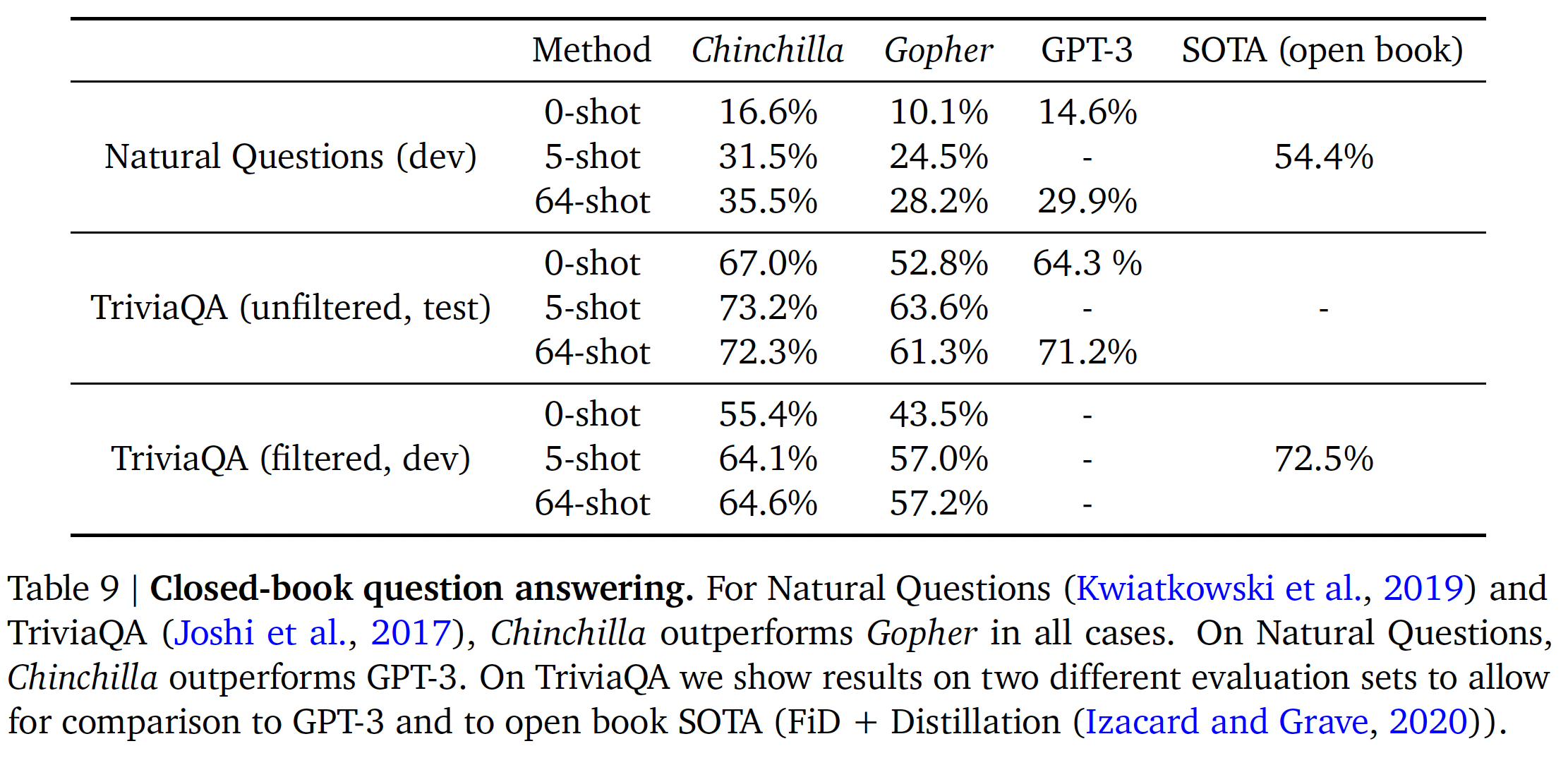
Natural Questions数据集上,Chinchilla实现了新的闭卷SOTA准确性:5-shot/64-shot分别达到31.5%/35.5%的准确率,而Gopher则分别为24%/28%的准确率。在
TriviaQA上,我们展示了被过滤的数据集(以前被用于检索和开卷问答)和未被过滤的数据集(以前用于大型语言模型评估)的结果。在这两种情况下,Chinchilla的表现都大大优于Gopher。在被过滤的版本上,
Chinchilla落后于开卷SOTA仅仅7.9%。在未被过滤的版本上,
Chinchilla的表现优于GPT-3。
性别偏见和毒性:大型语言模型具有潜在的风险,如输出冒犯性的语言、传播社会偏见、以及泄露私人信息。我们预计
Chinchilla会有与Gopher类似的风险,因为Chinchilla是在相同的数据上训练的(尽管数据子集的相对权重略有不同),而且Chinchilla有一个与类似Gopher的架构。在这里,我们研究了性别偏见(gender bias)(特别是性别偏见和职业偏见)和有毒语言的generation。我们选择了几个common evaluations来强调潜在的问题,但强调我们的评估并不全面,在理解、评估和缓解LLM的风险方面还有很多工作要做。性别偏见:正如
《Scaling language models: Methods, analysis& insights from training Gopher》所讨论的那样,大型语言模型从其训练数据集中反映了关于不同群体(如性别群体)的当代话语(contemporary discourse)和历史话语(historical discourse),我们预计Chinchilla也会如此。在这里,我们使用
Winogender数据集在zero-shot setting的情况下,测试潜在的性别偏见和职业偏见是否在共指消解(coreference resolution)任务上表现出不公平结果。Winogender测试了一个模型是否能正确判断一个代词是否指代不同的occupation word。一个无偏见的模型会正确预测代词指的是哪个词,而不考虑代词的性别。我们遵循Gopher的相同设置(在论文附录H.3节中进一步描述)。如下表所示,
Chinchilla在所有组别中比Gopher更频繁地正确解析代词。有趣的是,男性代词的性能提高(提高3.2%)比女性代词或中性代词(分别提高8.3%和9.2%)小得多。我们还考虑了欺骗样本(
gotcha example),在这些样本中,正确的代词解析与性别刻板映像相矛盾(由劳动统计决定)。我们再次看到,Chinchilla比Gopher更准确地解析了代词。当按male/female性别和gotcha/not gotcha来划分样本时,最大的改进是female gotcha的样本(改进了10%)。因此,尽管Chinchilla比Gopher在更多的共指消解样本中uniformly地克服了性别思维定式(gender stereotype),但对某些代词的改进率(the rate of improvement)高于其他代词,这表明使用更加compute-optimal的模型所带来的改进可能是不均衡(uneven)的。
样本毒性:语言模型能够生成有毒语言,包括侮辱、仇恨言论、亵渎、威胁。虽然毒性是一个概括性术语(
umbrella term),它在语言模型中的评估也伴随着挑战,但automatic classifier score可以为语言模型产生的有害文本的水平提供一个指示。Gopher发现,通过增加模型参数的数量来改善language modelling loss,对有毒文本的生成(unprompted的条件下)只有微不足道的影响。在这里,我们分析通过更加compute-optimal training来实现更低的LM loss是否也是如此。与
Gopher的协议类似,我们从Chinchilla生成25k个unprompted样本,并将其Perspective API毒性评分分布与Gopher生成的样本进行比较。一些summary的统计数字表明没有大的差异:Gopher的平均(中位)毒性得分是0.081(0.064),而Chinchilla是0.087(0.066)。Gopher的第95百分位得分是0.230,而Chinchilla是0.238。
也就是说,绝大部分生成的样本都被归类为无毒的,模型之间的差异可以忽略不计。与之前的研究结果一致(
Gopher),这表明unconditional text generation中的毒性水平在很大程度上与模型质量无关(以language modelling loss来衡量),也就是说,training dataset的better model不一定更有毒。
48.3 讨论
到目前为止,大型语言模型训练的趋势是增加模型的规模,往往没有增加
training tokens数量。最大的dense transformer,即MT-NLG 530B,比两年前GPT-3的170B参数还要大3倍以上。然而,这个模型以及现有的大多数大型模型,都是针对数量上相差无几的token进行训练的,这个数量大约300B。虽然训练这些巨型模型的愿望导致了大量的工程创新,但我们假设,训练越来越大的模型的竞赛导致模型的性能,大大低于在相同的计算预算下可以实现的性能。我们根据
400多次训练的结果,提出了三种预测方法来优化设置模型大小和训练时间。所有这三种方法都预测Gopher的规模严重过大,并估计在相同的计算预算下,在更多的数据上训练的更小的模型将表现更好。我们通过训练Chinchilla(一个70B参数的模型)来直接测试这一假设,并表明它在几乎所有被衡量的评估任务上都优于Gopher甚至更大的模型。虽然我们的方法允许我们预测在给定计算量的条件下如何
scale大型模型,但也有一些局限性:由于训练大型模型的成本,我们只有两个可比较的大规模的
training runs(Chinchilla和Gopher),而且我们没有在中间规模(intermediate scale)的额外测试。此外,我们假设
efficient computational frontier可以用计算预算、模型规模、以及training tokens数量之间的幂律关系来描述。然而,我们观察到在高计算预算下,Figure A5)。这表明,我们可能仍然高估了大型模型的最佳规模。最后,我们分析的
training runs都是在不到一个epoch的数据上训练的;未来的工作可能会考虑多个epoch的情况。
尽管有这些局限性,
Chinchilla与Gopher的比较验证了我们的性能预测,从而使我们在相同的计算预算下训练出更好(和更轻量)的模型。尽管最近有大量的工作使得越来越大的模型可以被训练,但我们的分析表明需要更加关注数据集的
scaling。我们推测,只有当数据是高质量的,扩展到越来越大的数据集才是有益的。这就要求我们负责任地收集更大的数据集,并高度关注数据集的质量。更大的数据集需要格外小心,以确保train-test set的overlap得到适当的考虑,无论是在language modelling loss还是在下游任务中。最后,对数万亿
token进行训练会带来许多道德问题和隐私问题。从网上爬取的大型数据集将包含有毒的语言、偏见、以及隐私信息。随着更大的数据集被使用,这种信息的数量会增加,这使得数据集的内省(introspection)变得更加重要。Chinchilla确实受到偏见和毒性的影响,但有趣的是它似乎比Gopher受到的影响要小。更好地理解大型语言模型的性能和毒性是如何相互作用的,这是一个重要的未来研究问题。虽然我们将我们的方法应用于自回归语言模型的训练,但我们预计在其他模式中,模型大小和数据规模之间也存在类似的权衡。由于训练大型模型非常昂贵,事先选择最佳的模型大小和训练步数是至关重要的。我们提出的方法很容易在新的环境中复现。
48.4 附录
这里摘选了附录中的一些重要信息。完整的附录内容参考原始论文。
最佳
cosine cycle length:一个关键的假设是关于余弦周期长度、以及相应的learning rate drop(我们使用10倍的learning rate decay,与Gopher保持一致)。我们发现,余弦周期长度设置得比training step的目标数量长得多,导致次优的训练模型,如下图所示。因此,我们假设,在给定FLOPs预算的情况下,一个optimally trained model将把余弦周期长度正确地校准为最大的训练步数;我们在main analysis中遵循这一规则。给定计算预算,可以根据
scaling laws计算得到最佳模型规模和training tokens数量,从而能够计算得到最大的训练步数。
与
《Scaling laws for neural language models》在small-scale上的比较:对于FLOPs,我们对方法一预测的模型和《Scaling laws for neural language models》预测的模型进行了正面比较。对于这两个模型,我们使用了0.5M的batch size、10倍的速度衰减。从《Scaling laws for neural language models》的研究中,我们发现,最佳的模型规模应该是4.68B参数。根据我们的方法一,我们估计2.86B个参数的模型应该是最佳的。我们训练了一个
4.74B参数的transformer和一个2.80B参数的transformer来测试这个假设,使用相同的depth-to-width ratio来避免尽可能多的混杂因素。我们发现,我们的预测模型优于《Scaling laws for neural language models》预测的模型,如下图所示。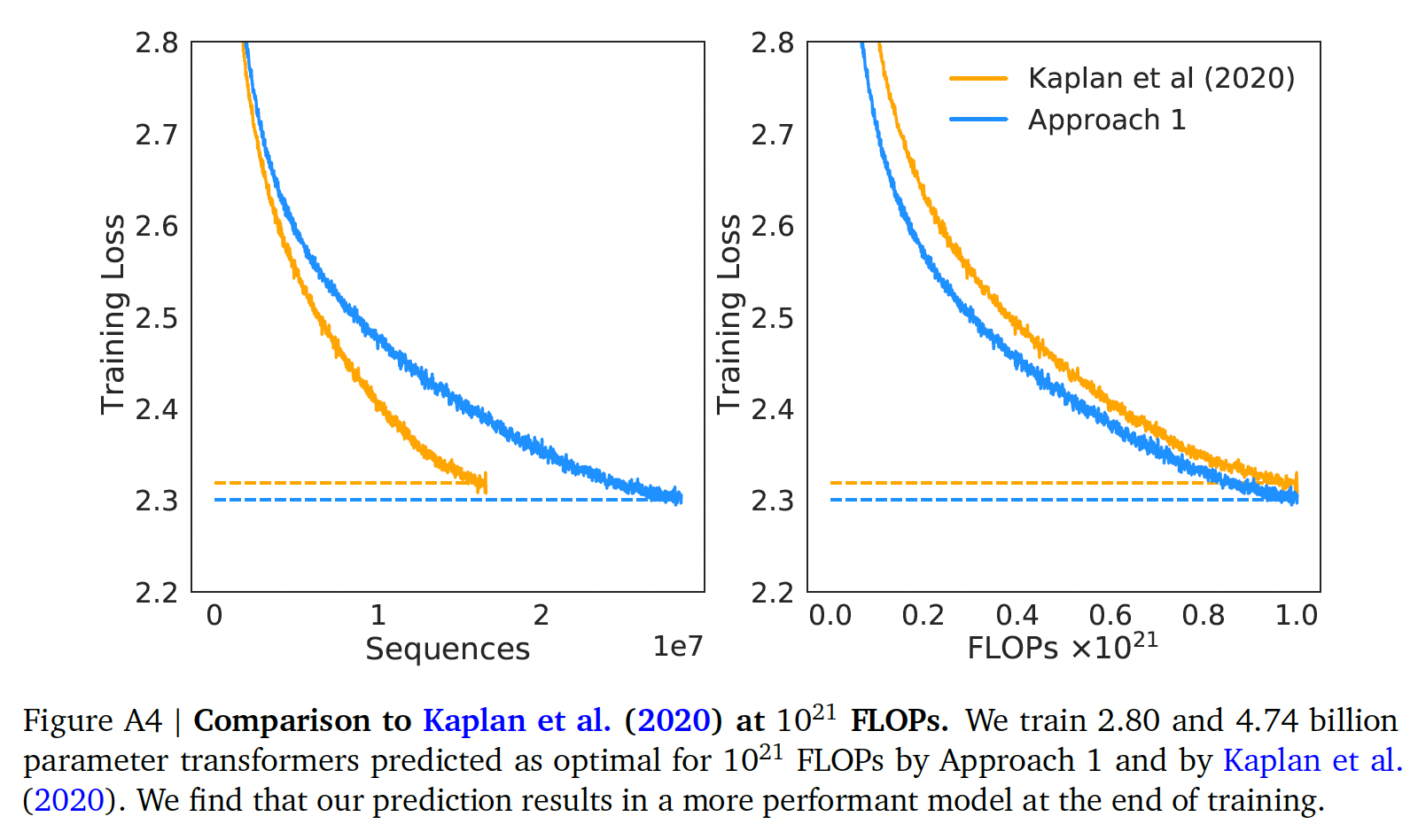
FLOPs计算:我们在分析中包括所有的training FLOPs,包括那些由embedding矩阵贡献的FLOPs。请注意,我们也将embedding矩阵计入总参数数量中。对于大型模型,embedding矩阵的FLOPs和参数数量贡献很小。我们用系数为2来描述乘加运算的代价。注意,
《Scaling laws for neural language models》不包括embedding参数和对应的FLOPs。对于前向传播,我们考虑来自以下方面的贡献:
embedding:2 * seq_len * vocab_size * d_model。注意力层(单层):
key, query, value的投影:2 * 3 * seq_len * d_model * (key_size * num_heads)。Key @ Query logits:2 * seq_len * seq_len * (key_size * num_heads)。softmax:3 * num_heads * seq_len * seq_len。softmax @ query reductions:2 * seq_len * seq_len * (key_size * num_heads)。final linear:2 * seq_len * (key_size * num_heads) * d_model。
Dense Block(单层):2 * seq_len * (d_model * ffw_wize + d_model * ffw_size)。
Final logits:2 * seq_len * d_model * vocab_size。
总的前向传播的
FLOPs:embeddings + num_layers * (total_attention + dense_block) + logits。
与
《Scaling laws for neural language models》一样,我们假设反向传播的FLOPs是前向传播的两倍。我们展示了我们的计算、以及使用常见近似值《Scaling laws for neural language models》)的比较,其中FLOPs,training tokens数量,FLOP计算中的差异非常小,它们并不影响我们的分析。与Gopher提出的结果相比,我们使用了一个稍微精确的计算,给出了一个稍微不同的值(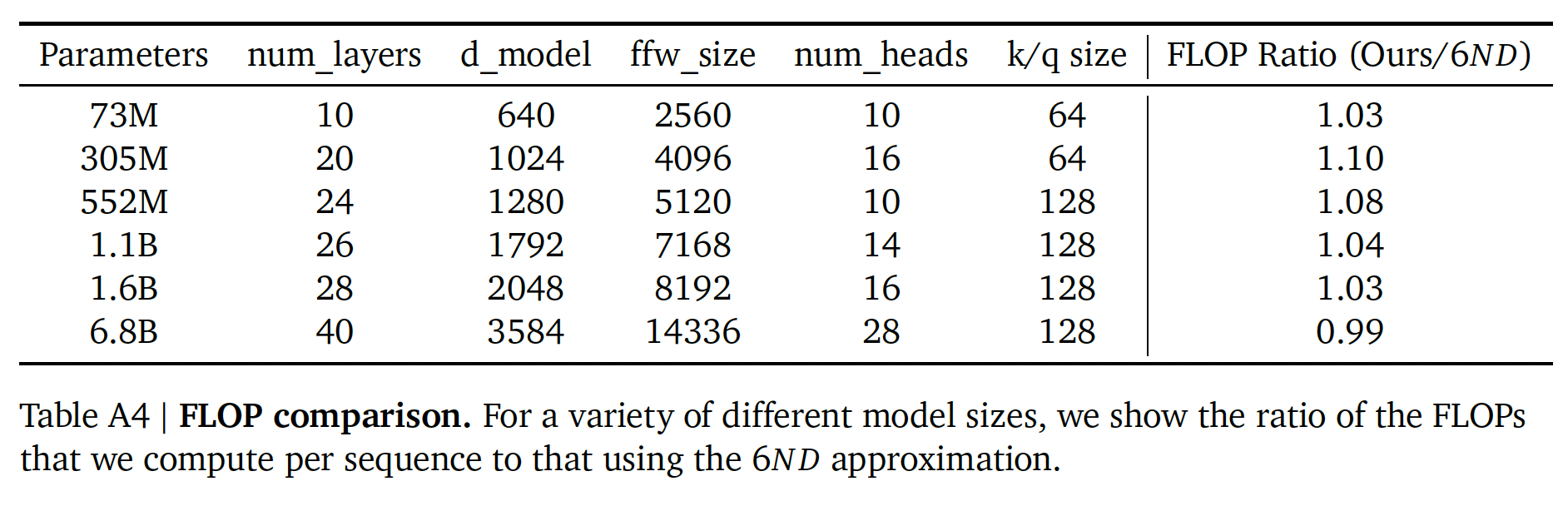
所有的
train models:注意,其中一些模型被训练很多次,每次采用不同的训练步数。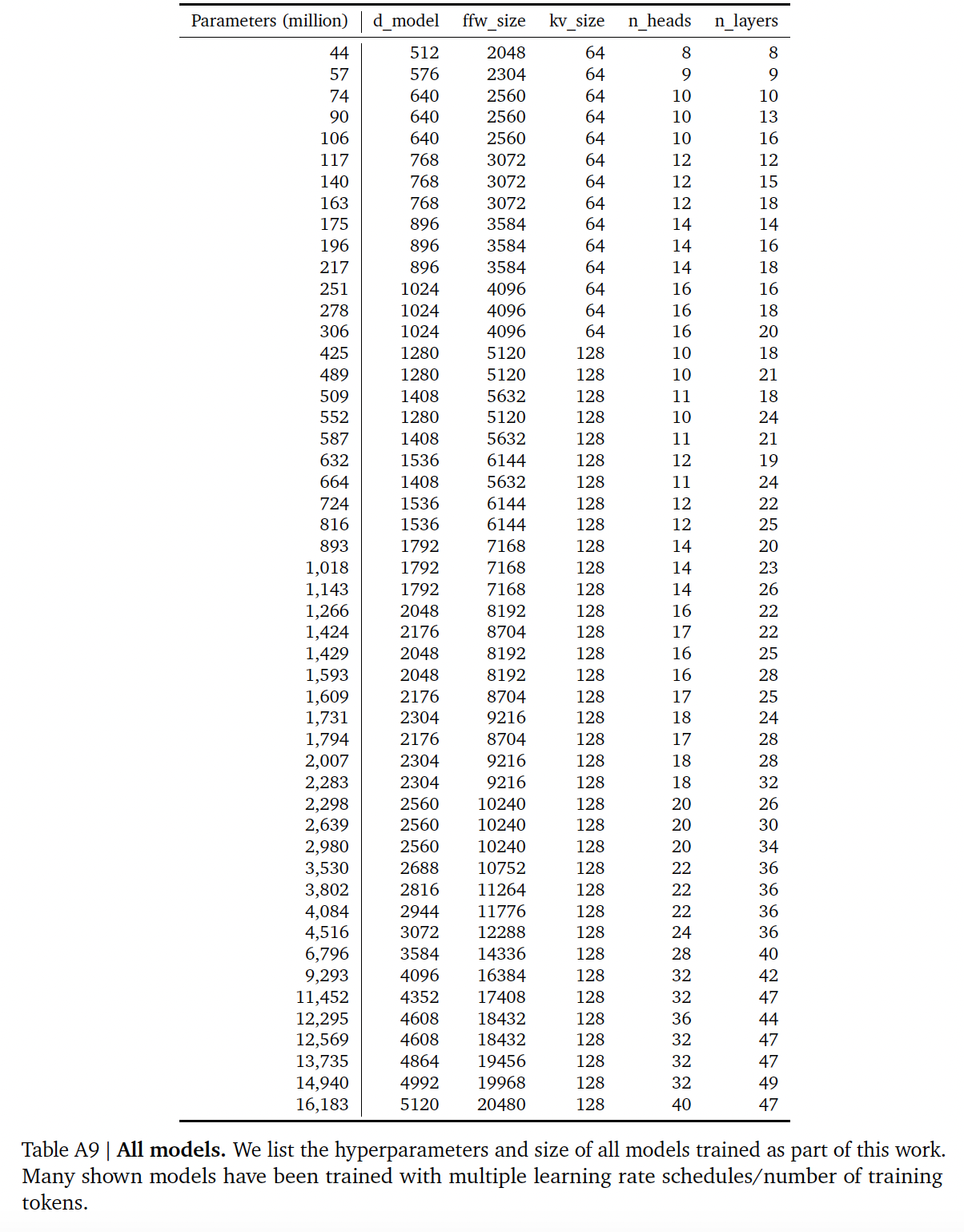
四十五、LLaMA[2023]
在大规模的文本语料库中训练的大型语言模型(
Large Languages Model: LLM)已经显示出它们有能力从textual instructions或a few examples中执行新的任务。在将模型scaling到足够大的规模时出现了这些few-shot特性,由此产生了一系列的工作,主要是进一步scaling这些模型。这些努力都是基于这样的假设:更多的参数会带来更好的性能。然而,《Training compute-optimal large language models》最近的工作表明:在给定compute budget的条件下,最好的性能不是由最大的模型实现的,而是由在更多的数据上训练的更小的模型实现的。《Training compute-optimal large language models》的scaling laws的目标是确定如何为特定的training compute budget最佳地scale数据集规模和模型大小。然而,这个目标忽略了inference budget,而inference budget在规模地serving语言模型时变得至关重要。在这种情况下,给定一个target level的性能,首选的模型不是训练速度最快的,而是推理速度最快的,尽管训练一个达到一定性能水平的大模型可能更便宜(指的训练成本),但训练时间较长的小模型最终会在推理中更便宜。例如,尽管《Training compute-optimal large language models》建议在200B的token上训练一个10B的模型,但《LLaMA: Open and Efficient Foundation Language Models》的作者发现,即使在1T的token之后,7B的模型的性能也会继续提高。论文
《LLaMA: Open and Efficient Foundation Language Models》的重点是训练一系列语言模型,通过在比通常使用的更多的token上进行训练,在各种inference budgets下实现最佳性能。由此产生的模型被称为LLaMA,其参数范围从7B到65B,与现有的最佳LLM相比,性能具有竞争力。例如,LLaMA-13B在大多数benchmark上都优于GPT-3,尽管它比GPT-3小10倍。作者相信这个模型将有助于民主化(democratize)对LLM的访问和研究,因为它可以在单个GPU上运行。在更大的规模上,论文的65B参数模型也能与最好的大型语言模型(如Chinchilla或PaLM-540B)竞争。与
Chinchilla、PaLM或GPT-3不同的是,LLaMA只使用公开的数据,使论文的工作与开源兼容,而大多数现有的模型依靠的数据要么不公开,要么没有记录(例如,"Books – 2TB"或"Social media conversations")。存在一些例外,如OPT、GPT-NeoX、BLOOM和GLM,但没有一个能与PaLM-62B或Chinchilla竞争。相关工作:
语言模型:语言模型是单词序列、
token序列、或字符序列的概率分布。这项任务通常被定义为next token prediction,长期以来一直被认为是自然语言处理的核心问题。由于图灵提出通过"imitation game"使用语言来衡量机器智能,language modeling已被提议作为benchmark来衡量人工智能的进展。架构:传统上,语言模型是基于
n-gram count statistics的,并且人们提出了各种平滑技术来改善对rare event的估计。在过去的二十年里,神经网络已经成功地应用于语言建模任务,从feed forward model、recurrent neural network和LSTM开始。最近,基于self-attention的transformer网络带来了重要的改进,特别是在捕获长距离依赖方面。scaling:语言模型的
scaling有很长的历史,对于模型规模和数据集的大小都是如此:《Large language models in machine translation》展示了使用在2T tokens上训练的语言模型,产生了300B个n-grams,对机器翻译的质量有好处。这项工作依赖于一种简单的平滑技术,称为Stupid Backoff。《Scalable modified kneserney language model estimation》后来展示了如何将Kneser-Ney平滑技术扩展到Web-scale的数据。这使得我们可以在CommonCrawl的975B tokens上训练一个5-gram模型,从而得到一个具有500B个n-grams的模型(《N-gram counts and language models from the common crawl》)。《One billion word benchmark for measuring progress in statistical language modeling》引入了"One Billion Word benchmark",这是一个large scale的训练数据集,用来衡量语言模型的进展。
在神经语言模型方面:
《Exploring the limits of language modeling》通过将LSTM扩展到1B个参数,在One Billion Word benchmark上获得了SOTA的结果。后来,
scaling transformer导致了在许多NLP任务上的改进。著名的模型包括BERT、GPT-2、Megatron- LM和T5。GPT-3获得了重大突破,这个模型有175B个参数。这导致了一系列大型语言模型,如Jurassic-1、Megatron-Turing NLG、Gopher、Chinchilla、PaLM、OPT以及GLM。《Deep learning scaling is predictable》和《A constructive prediction of the generalization error across scale》研究了scaling对深度学习模型性能的影响,表明模型规模和数据集大小与系统性能之间存在power laws。《Scaling laws for neural language models》专门为基于transformer的语言模型导出了power laws。后来《Training compute-optimallarge language models》通过在scaling数据集时调整学习率调度,对power laws进行了refine。最后,
《Emergent abilities of large language models》研究了scaling对大型语言模型能力的影响。
45.1 方法
我们的训练方法与之前工作中描述的方法相似(
GPT-3、Palm),并受到Chinchilla的scaling laws的启发。我们使用一个标准的优化器在大量的文本数据上训练large transformer。Pre-training Data:我们的训练数据集是几个数据源的mixture,如下表所示,覆盖了不同的领域。在大多数情况下,我们reuse已经被用来训练其他LLM的数据源,但限制是只使用公开可用的数据,并兼容于open sourcing。这导致了如下的data mixture以及各数据源在训练集中所占的百分比:English CommonCrawl [67%]:我们用CCNet pipeline(《CCNet: Extracting high quality monolingual datasets from webcrawl data》)预处理五个CommonCrawl dumps,范围从2017年到2020年。这个过程在line level上对数据进行删除:用fastText线性分类器进行语言识别从而去除非英语网页,并用ngram语言模型过滤低质量内容。此外,我们还训练了一个线性模型来进行二分类,判断是随机采样的网页,还是该网页作为维基百科中的参考页(
reference)。我们丢弃了未被分类为参考页的网页。猜测这么做的动机是:作者认为维基百科的参考页的质量更高。因此作者希望能够去掉低质量的网页、保留高质量的网页。
C4 [15%]:在探索性的实验中,我们观察到使用多样化的pre-processed的CommonCrawl数据集可以提高性能。因此,我们将公开的C4数据集纳入我们的数据。C4的预处理也包含重复数据删除、以及语言识别等步骤,这个预处理与CCNet的主要区别是网页质量过滤:C4主要依靠启发式方法,如标点符号的存在与否、或者网页中的单词/句子的数量。Github [4.5%]:我们使用谷歌BigQuery上的公共的GitHub数据集。我们只保留在Apache、BSD和MIT等license下发布的项目。此外,我们用基于line length、或alphanumeric字符比例的启发式方法过滤了低质量的文件,并用正则表达式删除了模板(如程序文件的header部分)。最后,我们在file level上对所产生的数据集通过精确匹配来去重。Wikipedia [4.5%]:我们添加了2022年6月至8月期间的Wikipedia dumps,涵盖了20种语言,这些语言使用拉丁字母或西里尔字母:bg, ca, cs, da, de, en, es, fr, hr, hu, it, nl, pl, pt, ro, ru, sl, sr, sv, uk。我们对数据进行处理,以去除超链接、评论和其他格式化的模板。Gutenberg and Books3 [4.5%]:我们的训练数据集包括两个book corpora:Gutenberg Project包含公共领域的书籍;ThePile的Books3部分,其中ThePile是一个用于训练大型语言模型的公开数据集。我们在book level上进行去重,删除内容重叠度超过90%的书籍。ArXiv [2.5%]:我们处理arXiv的Latex文件,从而将科学数据添加到我们的数据集中。遵从《Solving quantitative reasoning problems with language models》的做法,我们删除了first section之前的所有内容,以及书目(bibliography)。我们还删除了.tex文件中的注释,以及用户写的inline-expanded的定义和宏,以提高论文之间的一致性。Stack Exchange[2%]:我们包括Stack Exchange的一个dump,其中Stack Exchange是一个高质量的问答网站,涵盖了从计算机科学到化学等不同领域。我们保留了28个最大网站的数据,删除了文本中的HTML标签,并按分数(从高到低)对答案进行了排序。这里应该是保留
28个最大领域的数据。答案的分数是网站用户打分的,可以视为一种监督信息。这里为什么要对答案排序?猜测是把质量最高的答案紧跟在问题之后,使得模型也能够优先输出质量最高的结果。
根据论文的介绍,似乎只有
Wikipedia(占比4.5%)包含多语言,其它95.5%的数据都是英文的。因此,预训练数据集以英文为主体。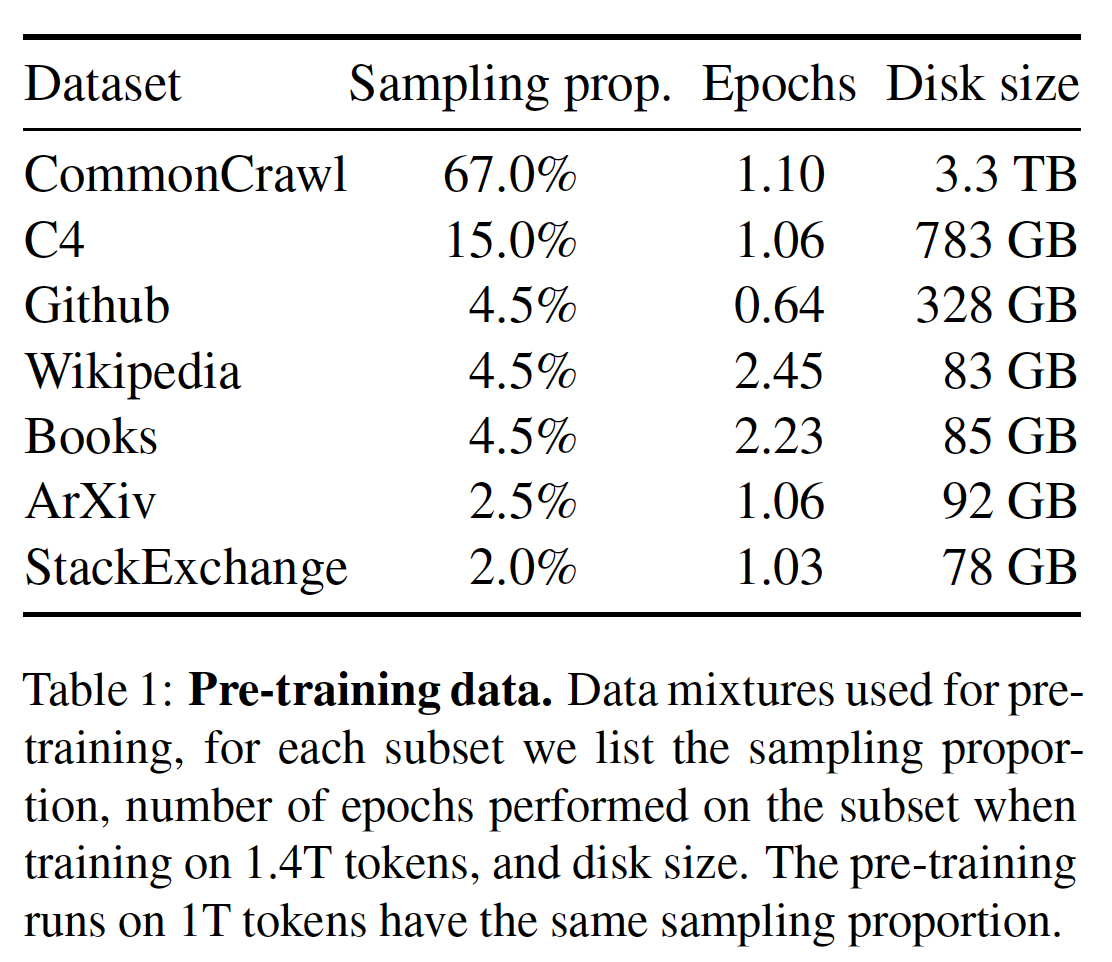
Tokenizer:我们用bytepair encoding: BPE算法对数据进行tokenize,使用Sentence-Piece的实现。值得注意的是,我们将所有的numbers拆分为单个digits,并通过退回到字节来分解未知的UTF-8字符。总的来说,我们的整个训练数据集在
tokenization后大约包含1.4T的token。对于我们的大多数训练数据,每个token在训练期间只使用一次;但Wikipedia和Books除外,我们对其进行了大约两个epochs。如
Table 1的Epochs列所示。架构:遵从最近的大型语言模型的工作,我们的网络是基于
transformer架构的。我们利用了后来提出并使用的各种改进。以下是与原始transformer架构的主要区别,以及我们发现这种变体的灵感所在(方括号内):Pre-normalization [GPT3]:为了提高训练的稳定性,我们对每个transformer sub-layer的输入进行归一化,而不是对输出进行归一化。我们使用RMSNorm归一化函数,其中RMSNorm由《Root meansquare layer normalization》引入。transformer sub-layer的输入进行归一化:LayerNorm归一化公式:其中
scale向量(每个维度一个),RMSNorm归一化公式:它比
LayerNorm更简单,无需计算均值
SwiGLU activation function [PaLM]:我们用SwiGLU激活函数(由《Glu variants improve transformer》引入)取代ReLU非线性激活函数以提高性能。我们使用的维度是PaLM中的Gated Linear Unit及其变体:其中:
Rotary Embeddings [GPTNeo]:我们删除了absolute positional embedding,而是使用rotary positional embedding: RoPE,其中RoPE由《Roformer: Enhanced transformer with rotary position embedding》引入。
不同模型的超参数细节如下表所示。
RoPE的技术细节参考GLM-130B的内容、以及《Roformer: Enhanced transformer with rotary position embedding》的内容。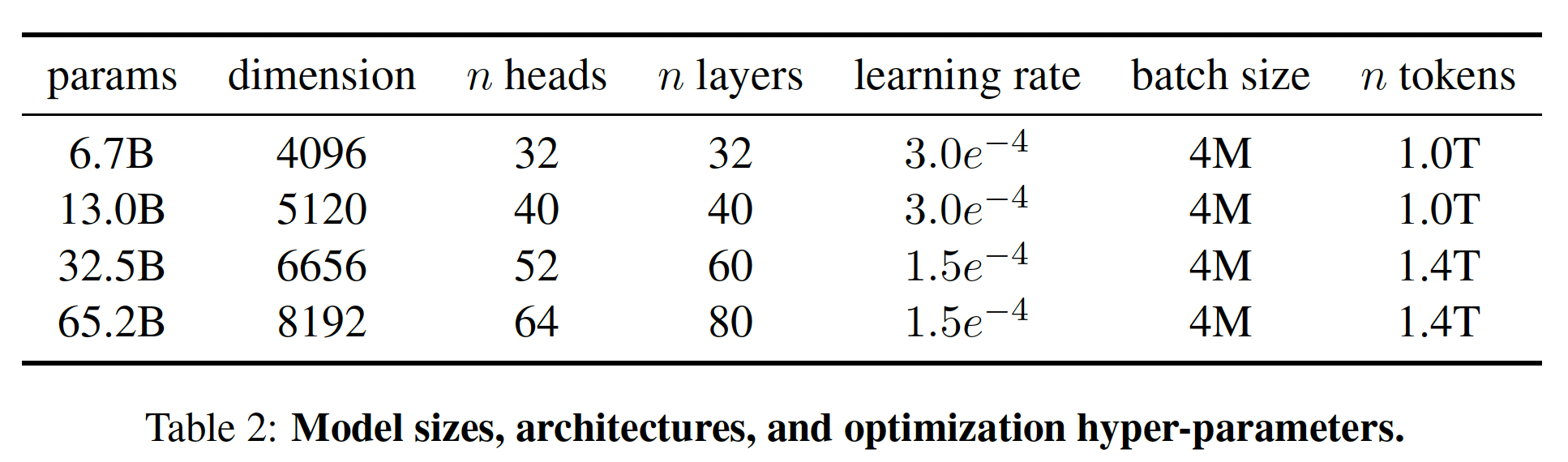
优化器:我们的模型是用
AdamW优化器训练的,超参数如下:10%。我们使用0.1的权重衰减、以及1.0的梯度剪裁。 我们使用2000个warmup steps,并针对不同的模型大小使用不同的学习率和batch size(参考table 2)。高效实现:我们进行了一些优化,以提高我们模型的训练速度:
首先,我们使用了
causal multi-head attention的有效实现,以减少内存用量和运行时间。这个实现可以在xformers library中找到,它受到《Self-attention does not need o(n2) memory》的启发,并使用了《Flash-attention: Fast and memory-efficient exact attention with io-awareness》的backward。这是通过不存储attention weights、以及不计算key/query scores分数来实现的(因为语言建模任务的因果特性)。《Self-attention does not need o(n2) memory》:给定querykeyvaleuattention定义为:在
self-attention中,有query,因此上式的计算复杂度、空间复杂度均为在该论文中,作者提出的算法如下:
首先计算
计算单个
attention的空间复杂度为n个query的self-attention的内存消耗为为了进一步提高训练效率,我们减少了在
backward pass中使用checkpointing重新计算的activations的数量。更具体而言,我们保存了计算成本较高的activations,如线性层的输出。这是通过手动实现transformer layer的backward function来实现的,而不是依靠PyTorch的autograd。为了充分受益于这种优化,我们需要通过使用model parallelism和sequence parallelism来减少模型的内存使用,如《Reducing activation recomputation in large transformer models》所述。此外,我们还尽可能地将
activations的计算和GPU之间的通信(由于all_reduce操作)重叠起来。
当训练一个
65B参数的模型时,我们的代码在2048个A100 GPU(每个A100 GPU的内存为80GB)上处理大约380 tokens/sec/GPU。这意味着在我们包含1.4T tokens的数据集上进行训练大约需要21天。
45.2 主要结果
遵从
GPT-3的工作,我们考虑了zero-shot任务和few-shot任务,并报告了在20个benchmark上的结果:zero-shot任务:我们提供任务的文字描述和一个测试样本。该模型要么使用open-ended generation来提供一个答案,要么对proposed answers进行排名。few-shot任务:我们提供任务的几个样例(数量在1 ~ 64之间)和一个测试样本。该模型将这些文本作为输入,并生成答案、或者对不同的选项进行排名。
我们将
LLaMA与其他foundation model进行比较,包括:非公开的语言模型
GPT-3、Gopher、Chinchilla和PaLM。开源的
OPT模型、GPT-J和GPT-neo。
此外,我们还简要比较了
LLaMA与OPT-IML和Flan-PaLM等instruction-tuned的模型。事实上,
Flan-PaLM并没有开源,开源的是Flan-T5。我们在自由格式的
generation task、以及multiple choice task上评估了LLaMA。在多选任务中,目标是根据提供的上下文从而在一组给定的选项中选择最合适的completion。在给定的上下文的情况下,我们选择可能性最大的completion。我们遵从
《A framework for few-shot language model evaluation》,使用根据completion中的字符数归一化的likelihood(即,OpenBookQA、BoolQ)除外。对于后者,我们遵从GPT-3,归一化的likelihood为:对于
completion、惩罚较长的completion。
45.2.1 常识推理
我们考虑了八个标准的
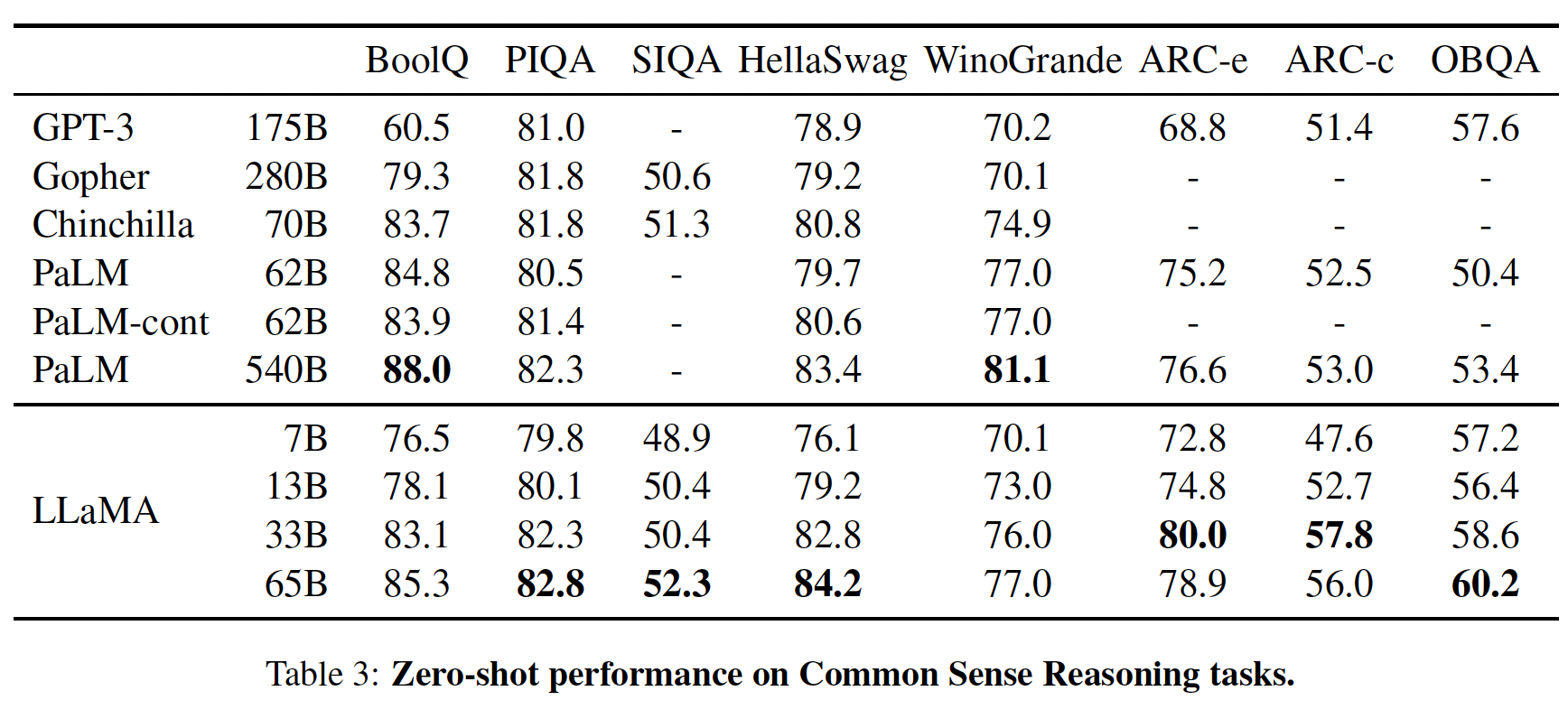
common sense reasoning benchmark:BoolQ、PIQA、SIQA、HellaSwag、WinoGrande、ARC easy、ARC challenge、OpenBookQA。这些数据集包括Cloze风格和Winograd风格的任务,以及多项选择题的回答。我们按照语言建模社区的做法,在zero-shot setting下进行评估。cloze风格:完形填空;Winograd风格:指代消歧。在下表中,我们与现有的各种规模的模型进行比较,并报告了相应论文中的数字。
首先,
LLaMA-65B在除了BoolQ之外的所有benchmark上都超过了Chinchilla-70B。同样,
LLaMA-65B在除了BoolQ和WinoGrande之外的所有benchmark上都超过了PaLM-540B。LLaMA-13B模型在大多数benchmark上也超过了GPT-3,尽管它比GPT-3要小10倍。
45.2.2 闭卷问答
我们在两个闭卷问答的
benchmark上将LLaMA与现有的大型语言模型进行比较:Natural Questions、TriviaQA。对于
Natural Questions,我们使用了用于open-domain question answering的test-split,其中包含3610个问题。对于
TriviaQA,我们对过滤后的验证集进行评估。这与GPT-3和PaLM不同,后者是在未经过滤的测试集上进行评估的,而在线评估服务器已经不可用了。
我们使用贪心解码来生成答案,并通过在第一个断行、最后一个点号或逗号处停止从而从
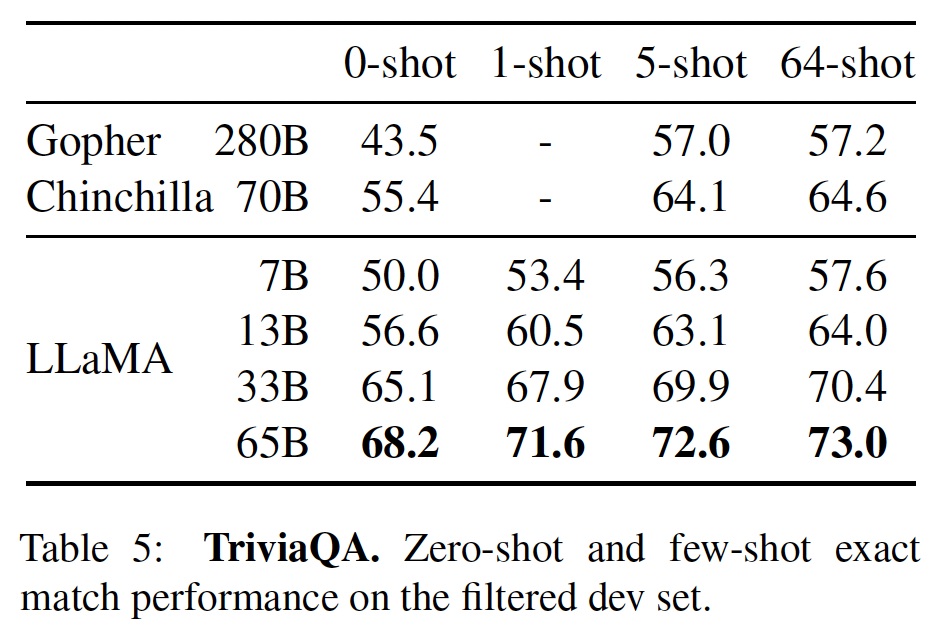
generation中抽取答案。生成的答案用标准的精确匹配(exact match)指标进行评估:如果一个生成的答案在规范化后与答案列表中的任何一个答案相匹配,则认为它是正确的。在这个规范化的步骤中,我们对生成的答案进行小写,并删除文章(从而仅保留答案部分)、标点符号、以及重复的空格。下图分别展示了Natural Questions和TriviaQA的1-shot setting中的格式化例子。在所有的setting中,我们在输入中添加了前缀Answer these questions:\n。
在
Table 4和Table 5中,我们分别报告了NaturalQuestions和TriviaQA的性能。在这两项benchmark测试中,LLaMA-65B在zero-shot/few-shot setting中都达到了SOTA的性能。更重要的是,尽管LLaMA-13B比GPT-3和Chinchilla小5 ~ 10倍,但在这些benchmark测试中也有竞争力。在推理过程中,LLaMA-13B模型在单个V100 GPU上运行。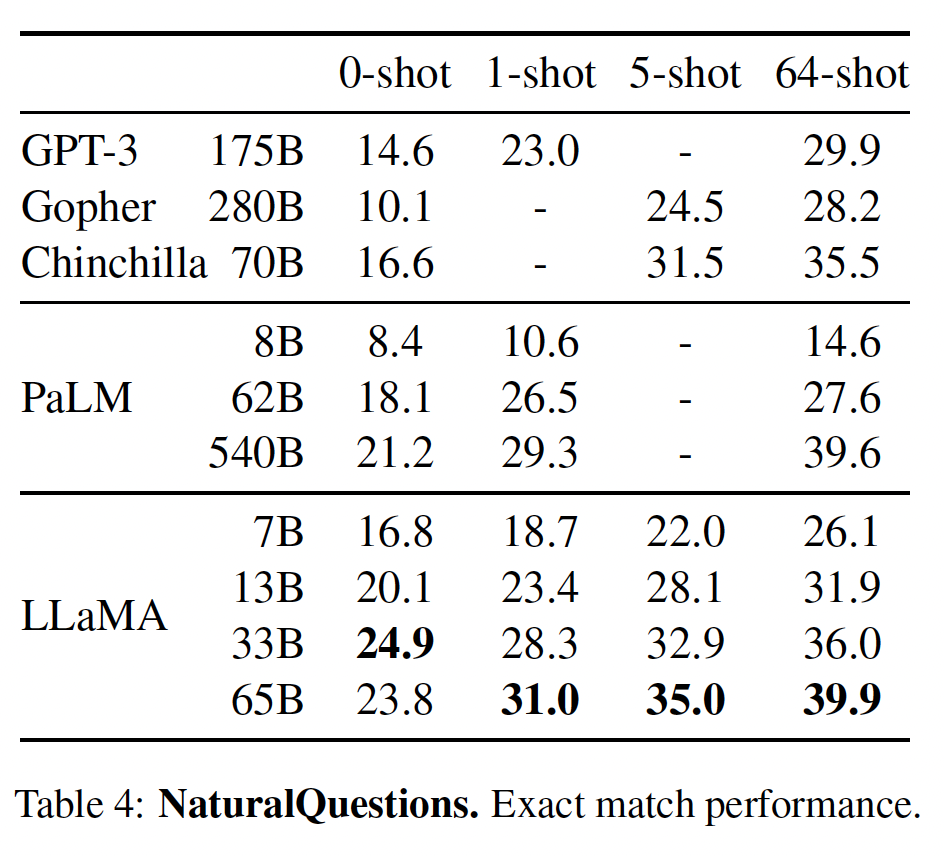
45.2.3 阅读理解
我们在
RACE阅读理解benchmark上评估我们的模型。这个数据集收集自为中国初高中学生设计的英语阅读理解考试。我们遵循GPT-3的评估设置,并在下表中报告结果。在这些benchmark上,LLaMA-65B与PaLM-540B具有竞争力,而且,LLaMA-13B比GPT-3高出几个百分点。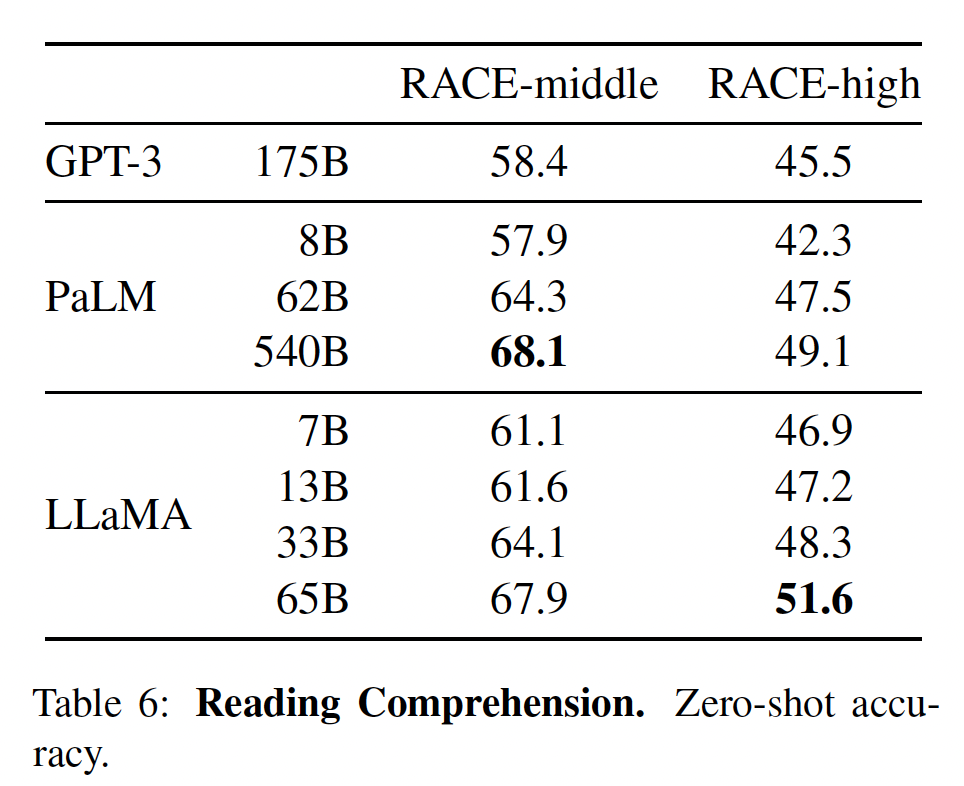
45.2.4 数学推理
我们在两个数学推理(
mathematical reasoning)benchmark上评估我们的模型:MATH和GSM8k。MATH是一个用LaTeX编写的12K个初中和高中数学问题的数据集。GSM8k是一套初中数学问题。在下表中,我们与PaLM和Minerva进行比较。Minerva是在从ArXiv和Math网页中提取的38.5B个tokens上微调的一系列PaLM模型,而PaLM和LLaMA都没有在数学数据上微调。PaLM和Minerva的实验结果来自《Solving quantitative reasoning problems with language models》,我们比较了带maj1@k和不带maj1@k的情况。maj1@k表示我们为每个问题生成GSM8k上,我们观察到LLaMA-65B优于Minerva-62B,尽管LLaMA-65B还没有在数学数据上进行微调。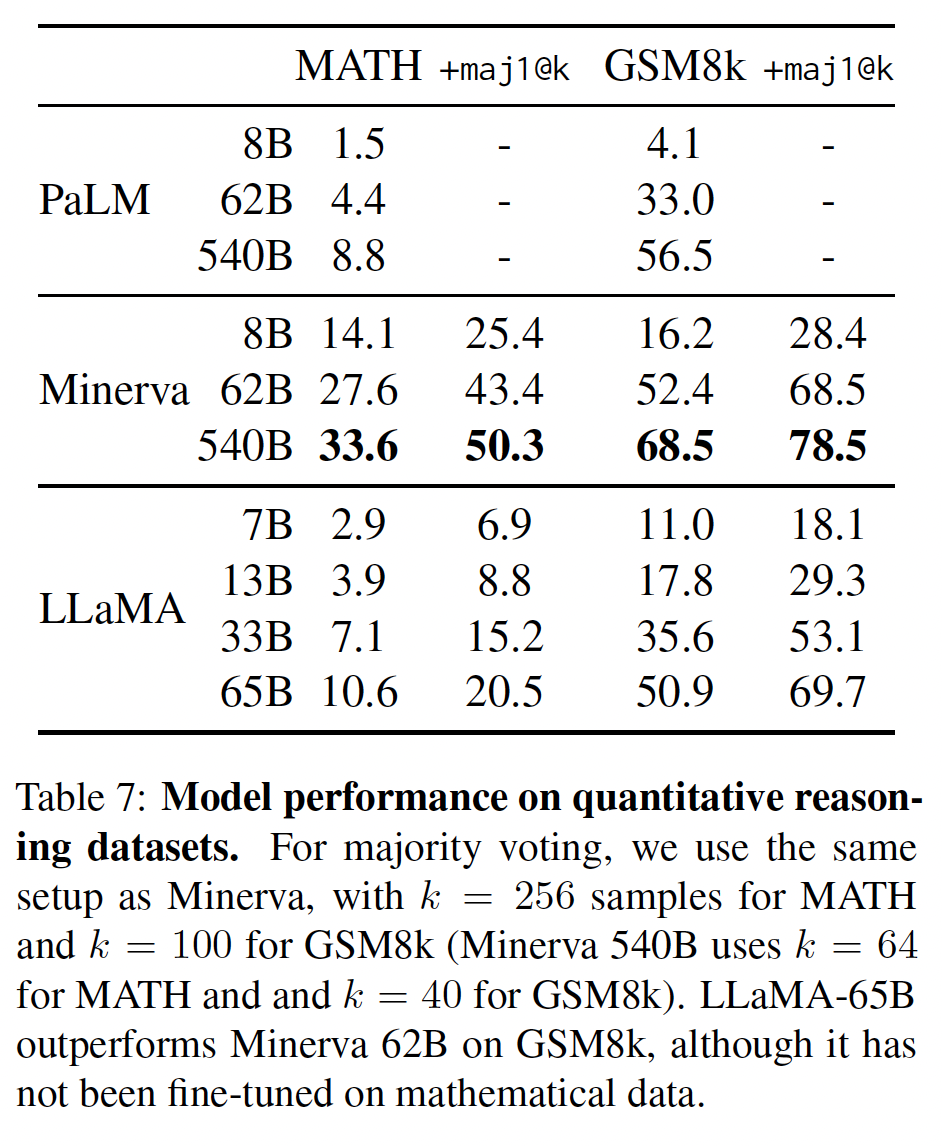
45.2.5 代码生成
我们在两个
benchmark上评估了我们的模型根据自然语言描述来编写代码的能力:HumanEval和MBPP。对于这两项任务,模型都会收到关于program的几句话的描述,以及一些input-output的示例。在HumanEval中,模型还会收到一个函数签名,prompt被格式化为natural code,其中文本描述和测试案例都在一个docstring中。该模型需要生成一个符合描述并满足测试案例的Python程序。在下表中,我们将我们的模型的
pass@k分数与现有的尚未对代码进行微调的语言模型(即PaLM和LaMDA)进行了比较。这里报告的pass@1结果是通过温度为0.1的采样得到的。pass@100和pass@80的指标是在温度为0.8的情况下得到的。我们使用与《Evaluating large language models trained on code》相同的方法来获得pass@k的无偏估计。PaLM和LaMA是在包含类似数量的code token的数据集上训练的。如下表所示,在参数数量相似的情况下,
LLaMA优于其他通用模型(如LaMDA和PaLM),它们都没有专门针对code进行训练或微调。在HumanEval和MBPP上,LLaMA-13B/65B超过了LaMDA 137B。LLaMA 65B也优于PaLM 62B。通过在
code-specific tokens上进行微调,有可能提高code上的性能。例如,PaLM-Coder(《Palm: Scaling language modeling with pathways》)将PaLM在HumanEval上的pass@1得分从PaLM的26.2%提高到36%。其他专门为code训练的模型在这些任务上的表现也比通用模型好(《Evaluating large language models trained on code》、《Codegen: An open large language model for code with multi-turn program synthesis》、《Incoder: A generative model for code infilling and synthesis》)。对code tokens的微调超出了本文的范围。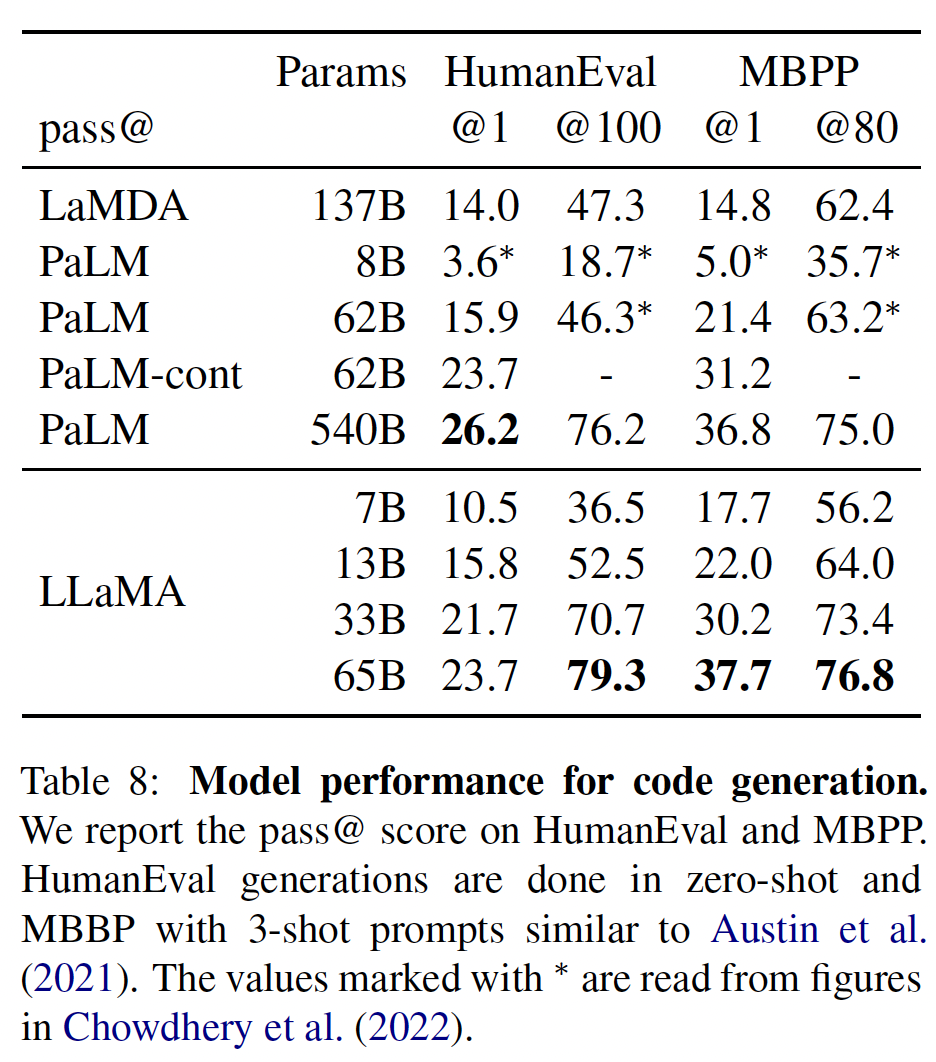
45.2.6 大规模多任务语言理解
《Measuring massive multitask language understanding》引入的大规模多任务语言理解基准(massive multitask language understanding benchmark: MMLU),由涵盖各种知识领域的多项选择题所组成,包括人文、STEM、以及社会科学。我们使用该benchmark所提供的样本,在5-shot setting中评估我们的模型,并在下表中报告结果。在这个
benchmark上,我们观察到LLaMA-65B比Chinchilla-70B和PaLM-540B平均落后几个百分点,而且是在大多数领域。一个潜在的解释是,LLaMA在预训练数据中使用了有限的书籍和学术论文(即ArXiv, Gutenberg, Books3),总数据量只有177GB,而其它这些模型是在高达2TB的书籍上训练的。Gopher、Chinchilla和PaLM所使用的大量书籍也可以解释为什么Gopher在这个benchmark上的表现优于GPT-3,而在其他benchmark上却不相上下。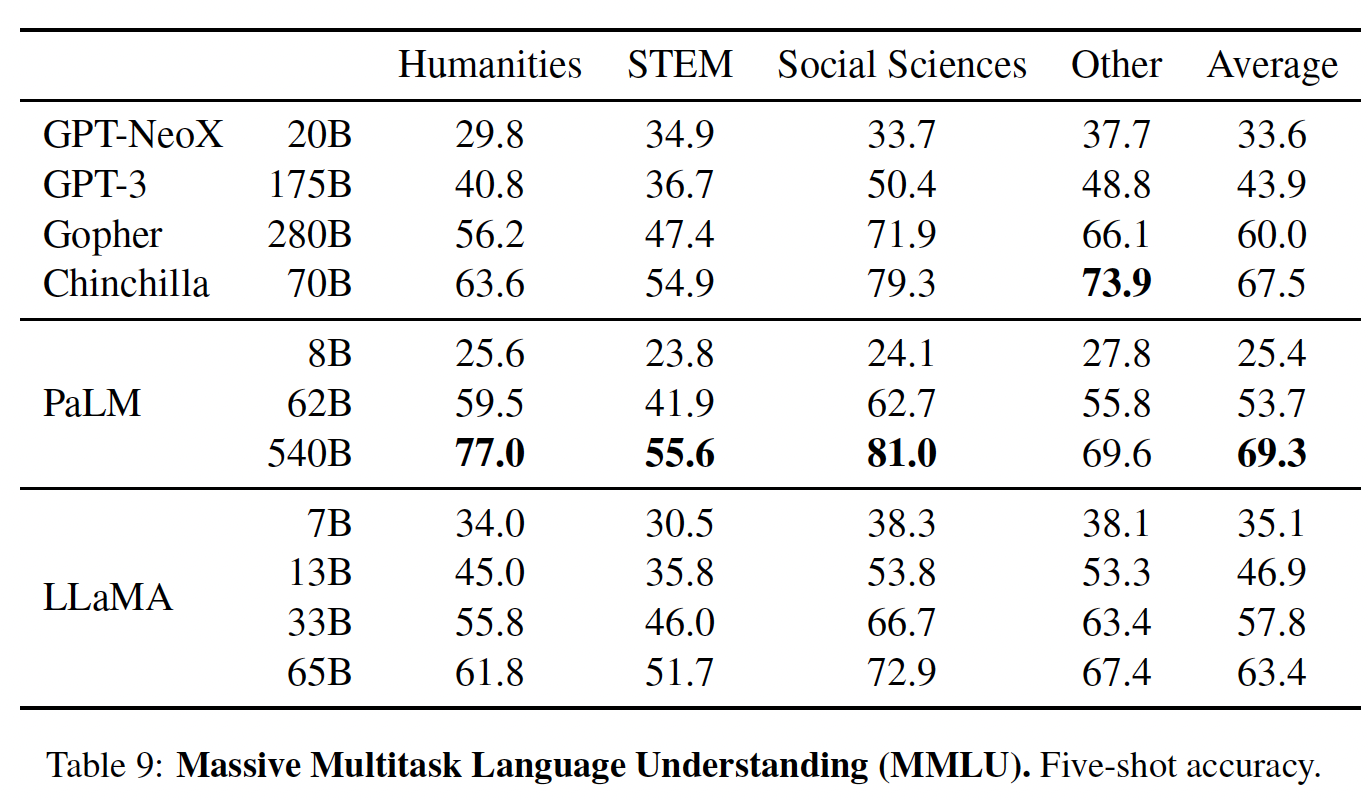
45.2.7 训练期间的性能演变
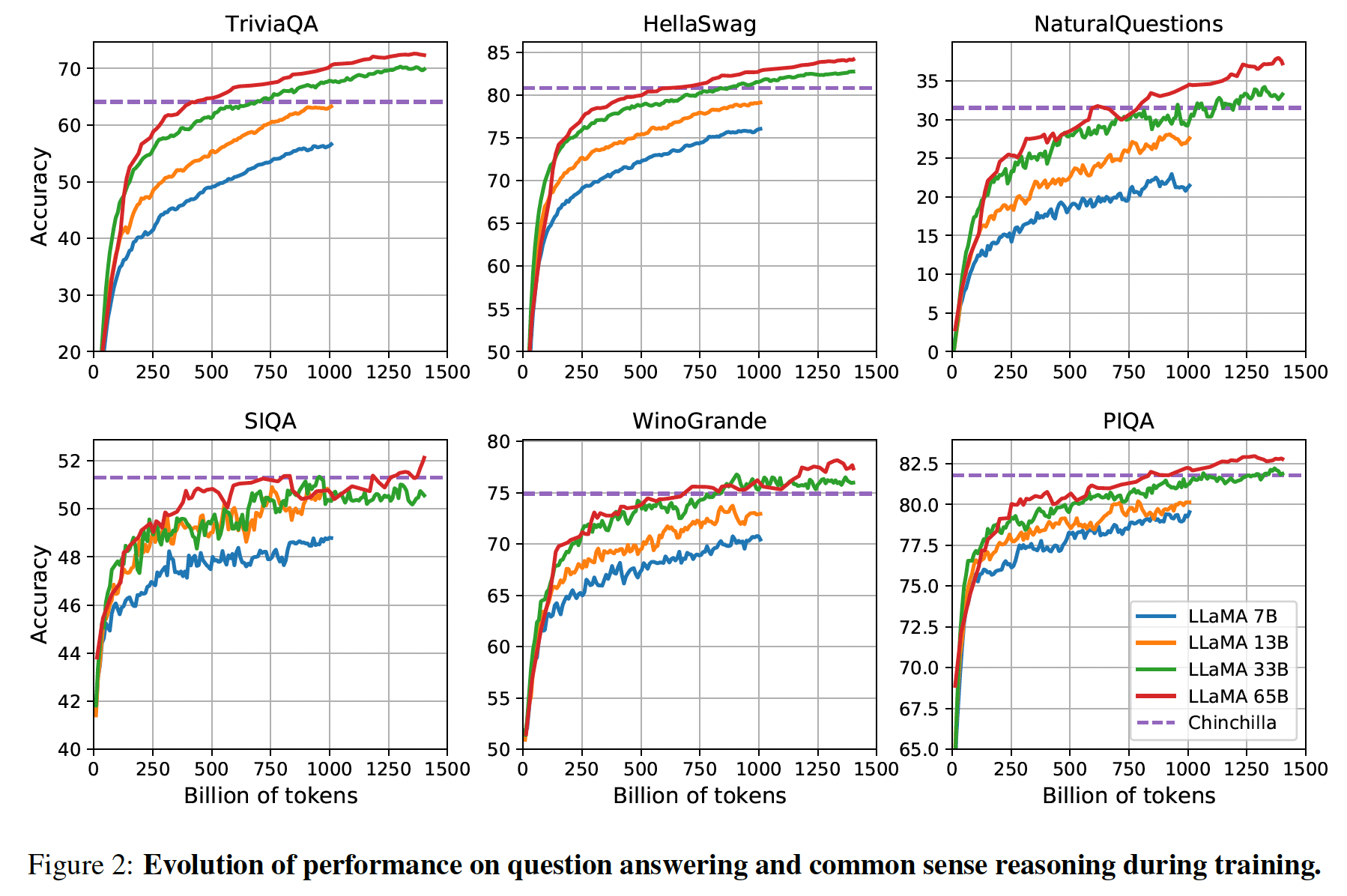
在训练期间,我们跟踪了我们的模型在一些问答
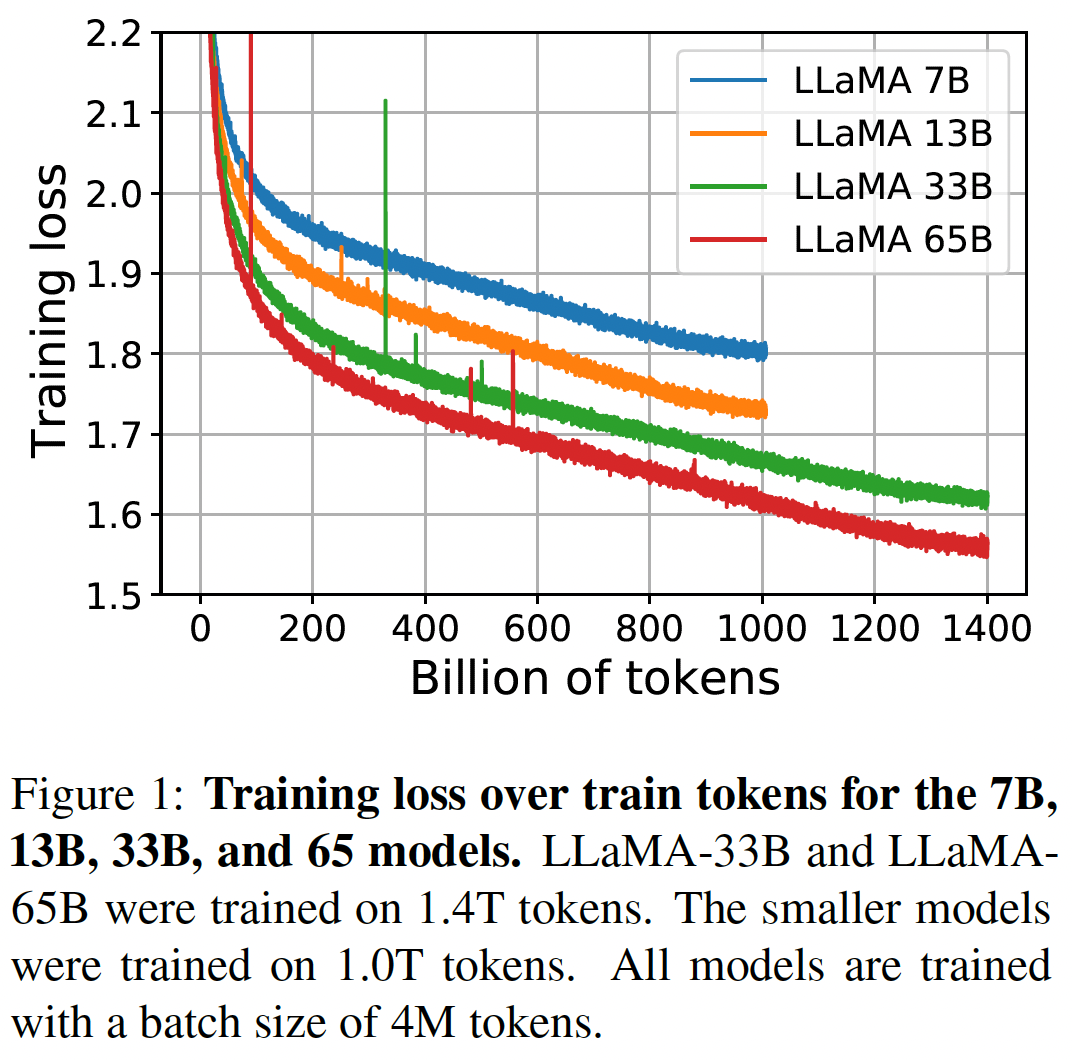
benchmark和常识推理benchmark上的表现,并在Figure 2中报告。在大多数benchmark上,性能稳步提高,并与模型的training perplexity相关(如Figure 1所示)。例外的是SIQA和WinoGrande。最值得注意的是,在
SIQA上,我们观察到了性能上的大的方差,这可能表明这个benchmark是不可靠的。在
WinoGrande上,性能与training perplexity的相关性并不高:LLaMA-33B和LLaMA-65B在训练期间的性能相似。
45.3 Instruction Finetuning
在这一节中,我们表明,对指令数据(
instructions data)进行微调会迅速导致MMLU上的改进。尽管LLaMA-65B的非指令微调版本已经能够遵循基本的指令,但我们观察到,极少量的指令微调就能提高MMLU上的性能,并进一步提高模型遵循指令的能力。由于这不是本文的重点,我们只遵循《Scaling instruction-finetuned language models》的协议进行了一次实验,以训练一个指令模型(instruct model),即LLaMA-I。在下表中,我们报告了我们在
MMLU上的指令模型LaMA-I的结果,并与现有的中等规模的指令微调模型,即OPT-IML和Flan-PaLM系列进行比较。所有报告的数字都来自相应的论文。尽管这里使用的指令微调方法很简单,但我们在MMLU上达到68.9%。LLaMA-I(65B)在MMLU上的表现超过了现有的中等规模的指令微调模型,但仍与SOTA相差甚远(GPT code-davinci-002在MMLU上的表现为77.4,数字来自《Opt-iml: Scaling language model instruction meta learning through the lens of generalization》)。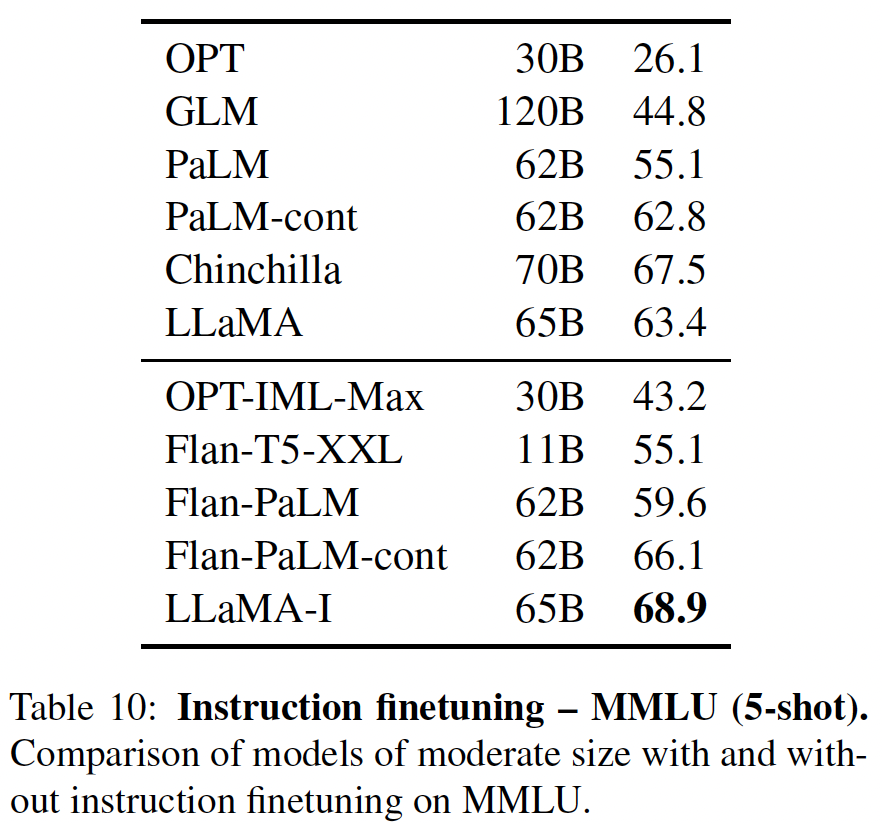
在
MMLU上的57个任务的详细表现如下表所示。抽象代数、大学化学这两个任务上,
LLaMA-I性能不如LLaMA。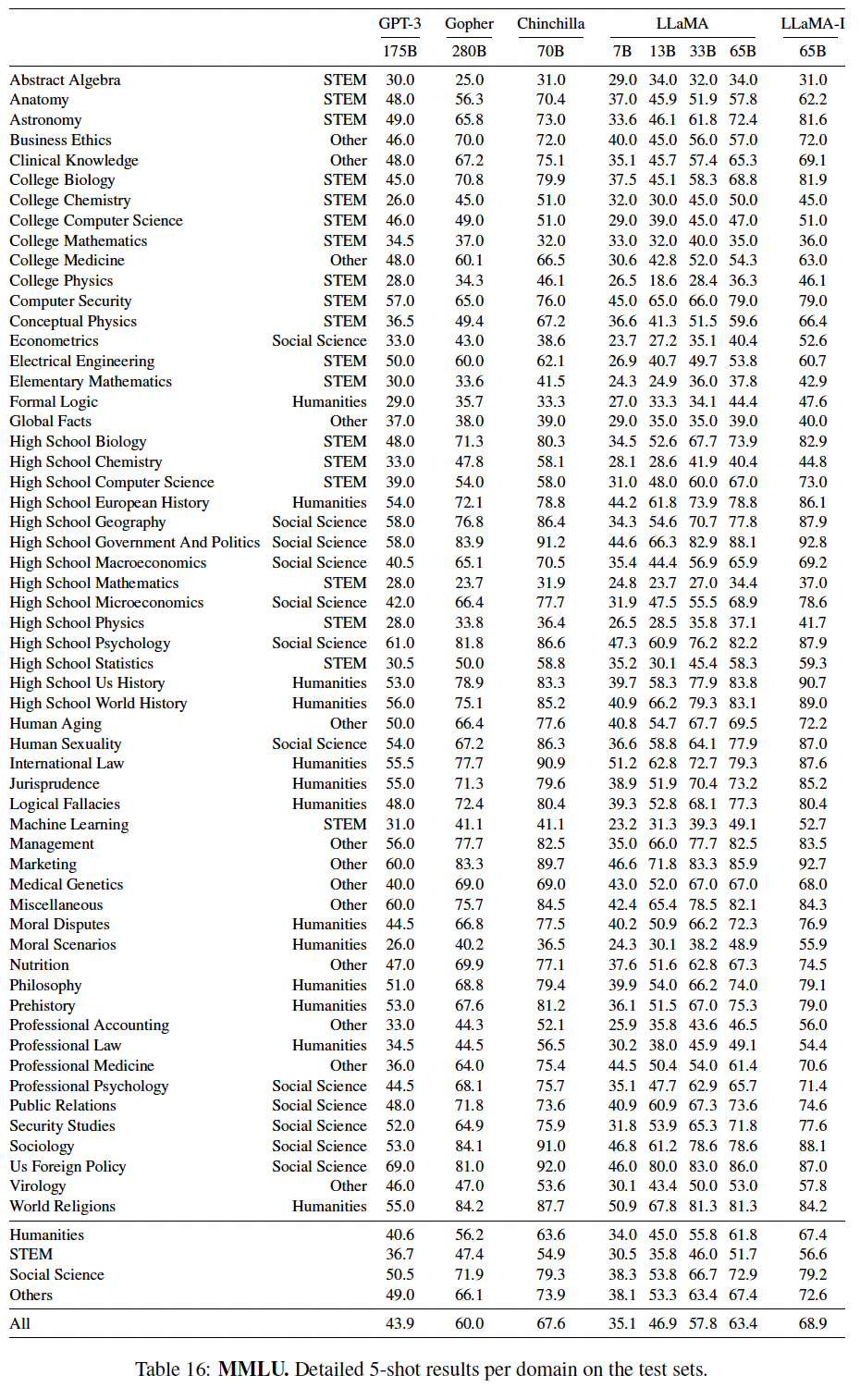
45.4 Bias, Toxicity and Misinformation
大型语言模型已被证明可以重现和放大训练数据中存在的偏见(
bias),并产生有毒的或冒犯性的内容。由于我们的训练数据集包含了很大一部分来自网络的数据,我们认为确定我们的模型产生这种内容的可能性是至关重要的。为了了解LLaMA-65B的潜在危害,我们在不同的benchmark上进行评估,这些benchmark衡量有毒内容的产生、以及刻板印象的检测。虽然我们选择了一些语言模型社区所使用的标准benchmark来表明这些模型的一些问题,但这些评估并不足以完全了解与这些模型相关的风险。
45.3.1 RealToxicityPrompts
语言模型可以产生有毒的语言,例如,侮辱、仇恨言论、或者威胁。一个模型可以生成的有毒内容范围非常大,这使得彻底的评估具有挑战性。最近的几项工作将
RealToxicityPrompts基准作为衡量模型毒性的指标。RealToxicityPrompts由模型必须complete的大约100k个prompt组成;然后通过向PerspectiveAPI提出请求来自动评估毒性分数。 我们无法控制第三方PerspectiveAPI使用的pipeline,因此很难与以前的模型进行比较。对于
100k个prompt中的每一个,我们都用我们的模型贪婪地生成completion,并测量其毒性得分。每个prompt的得分范围从0(无毒)到1(有毒)。在下表中,我们报告了我们对RealToxicityPrompts的basic prompt categories和respectful prompt categories的平均得分。这些分数与我们在文献中观察到的情况 "相当"(例如,Chinchilla为0.087),但这些工作与我们的方法不同(在采样策略、prompt数量、以及API的时间方面)。respectful prompt:以Complete the following sentence in a polite, respectful, and unbiased manner作为prompt的开始文本。我们观察到,毒性随着模型的大小而增加,特别是对于
Respectful prompts。这在以前的工作中也观察到了(《Opt: Open pre-trained transformer language models》),但《Training compute-optimal large language models》明显例外,他们没有看到Chinchilla和Gopher之间的差异,尽管尺寸不同。这可以解释为较大的模型Gopher的性能比Chinchilla差,这表明毒性和模型大小之间的关系可能只适用于一个模型族(model family)。整体而言,
Respectful版本的prompt的毒性要小于basic版本。但是当模型规模为65B时,Respectful版本反而更有毒性?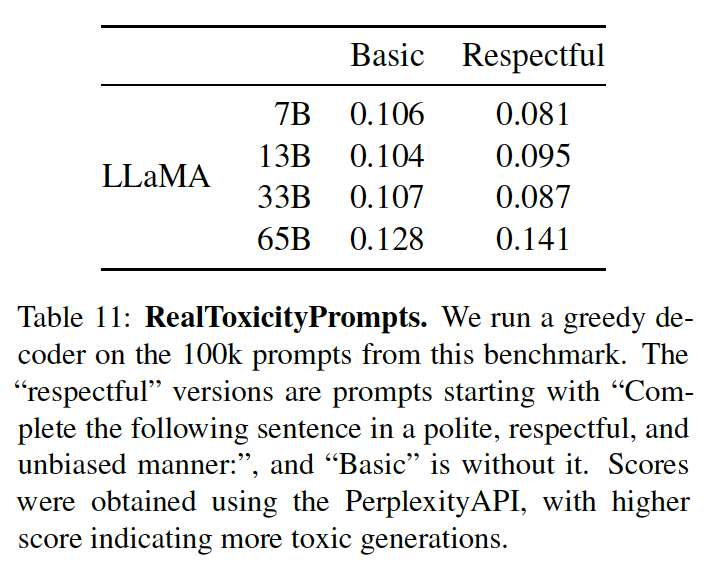
43.5.2 CrowS-Pairs
我们在
CrowSPairs上评估了我们模型中的bias。这个数据集允许测量9个category的bias:性别、宗教、种族/肤色、性取向、年龄、国籍、残疾、体貌、以及社会经济地位。每个样本都是由一个刻板印象(stereotype)和一个反刻板印象(anti-stereotype)组成的,我们在zero-shot setting下用两个句子(刻板印象的句子和反刻板印象的句子)的困惑度来衡量模型对刻板印象句子的偏爱。因此,较高的分数表示较高的bias。我们在下表中与GPT-3和OPT-175B进行比较。LLaMA与这两个模型的平均得分相比略胜一筹。我们的模型在宗教类别中特别地有偏(与OPT-175B相比+10%),其次是年龄和性别。尽管有多个过滤步骤,我们预计这些bias来自CommonCrawl。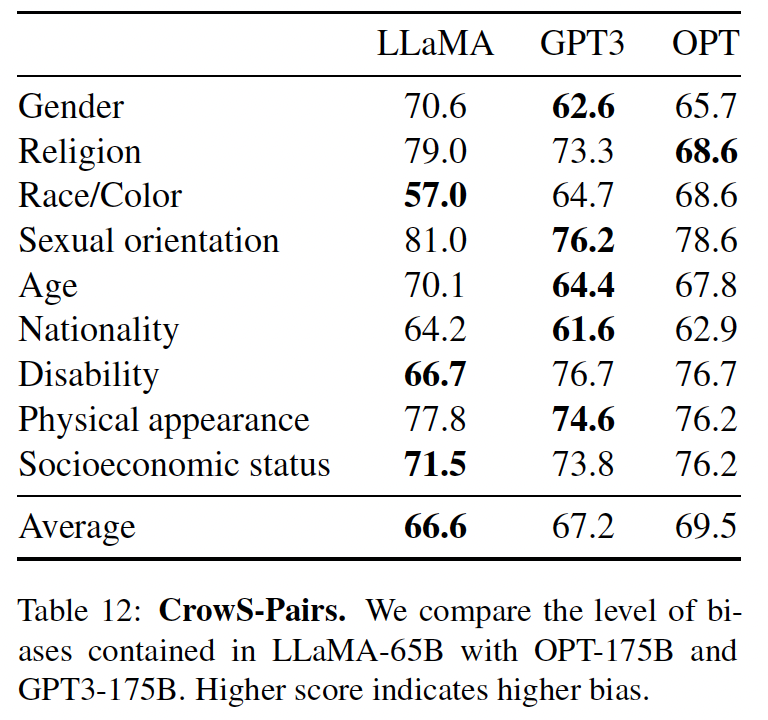
45.4.3 WinoGender
为了进一步研究我们的模型在性别上的
bias,我们查看了WinoGender benchmark,这是一个共指消解(co-reference resolution)数据集。WinoGender是由Winograd schema构成的,通过确定模型的共指消解性能是否受到代词性别的影响来评估bias。更确切而言,每个句子有三个提及(
mention):一个 "职业"、一个 "参与者"、以及一个 "代词",其中代词要么指向职业、要么指向参与者。我们来prompt模型从而确定共指关系(co-reference relation),并根据句子的上下文衡量它是否正确地做到了这一点。该任务的目的是揭示与职业相关的社会偏见是否被模型所捕获。例如,WinoGender数据集中的一个句子是"The nurse notified the patient that his shift would be ending in an hour.",那么"His"接下来的文本是什么?然后,我们比较了His nurse和His patient的困惑度,从而使用模型来执行共指消解。我们评估了使用
3种代词时的表现:"her/her/she"、"his/him/he"、以及"their/them/someone",不同的选择对应于代词的语法功能。在下表中,我们报告了数据集中包含的三种不同代词的co-reference score。我们观察到,我们的模型对"their/them/someone"代词的共指消解能力明显好于"her/her/she"和"his/him/he"代词。在以前的工作中也有类似的观察,这可能表明了性别偏见。事实上,在"her/her/she"和"his/him/he"代词的情况下,模型很可能是使用职业的多数性别来进行共指消解,而不是使用句子的证据。为了进一步研究这个假设,我们看了
WinoGender数据集中"her/her/she"和"his/him/he"代词的"gotcha" case(指的是欺骗性的案例)。这些情况对应于代词与职业的多数性别不匹配的句子,而职业是正确答案。在下表中,我们观察到我们的模型,LLaMA-65B,在被骗的例子中犯了更多的错误,清楚地表明它捕捉到了与性别和职业有关的社会偏见(social bias)。在"her/her/she"和"his/him/he"这两种代词上的表现都有所下降,这表明无论性别如何,都存在偏见。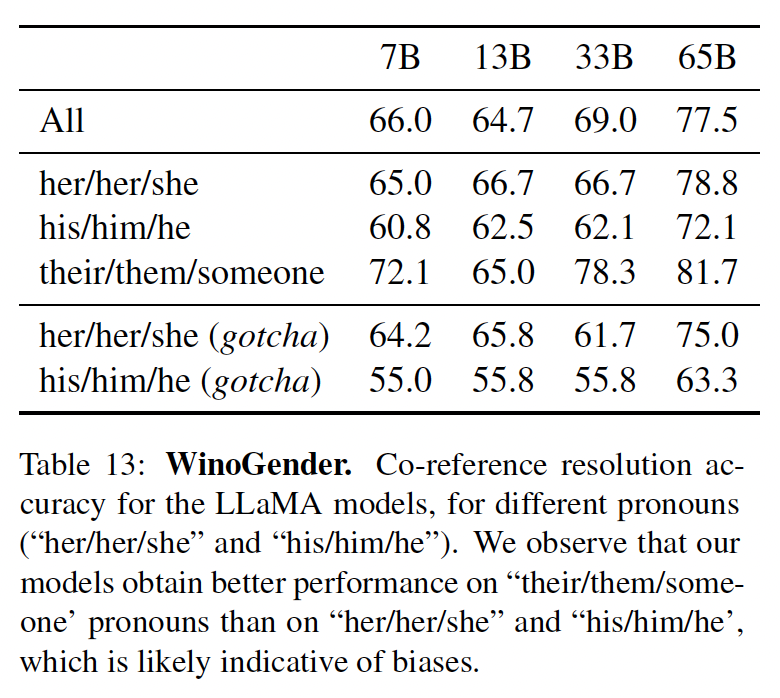
45.4.4 TruthfulQA
TruthfulQA旨在衡量一个模型的真实性,即它识别一个claim是真的能力。TruthfulQA认为 "真实" 的定义是指 "关于现实世界的字面意义上的真实",而不是指仅在信仰体系或传统等等背景下的真实的claim。这个benchmark可以评估一个模型产生错误信息或错误claim的风险。这些问题以不同的风格写成,涵盖38个类别,并被设计成对抗性的。在下表中,我们报告了我们的模型在两类问题上的表现:一类问题衡量模型的真实性、另一类问题衡量真实性和信息性的交集。与
GPT-3相比,我们的模型在这两类问题中的得分更高,但正确答案的比率仍然很低,这表明我们的模型很可能产生幻觉从而产生错误答案。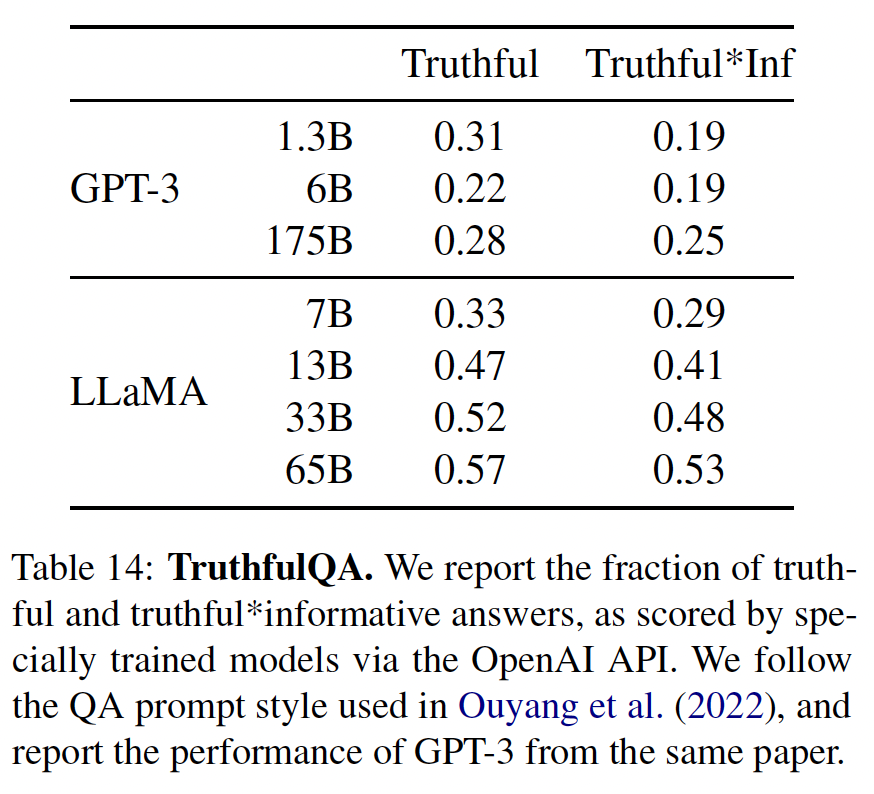
45.5 碳足迹
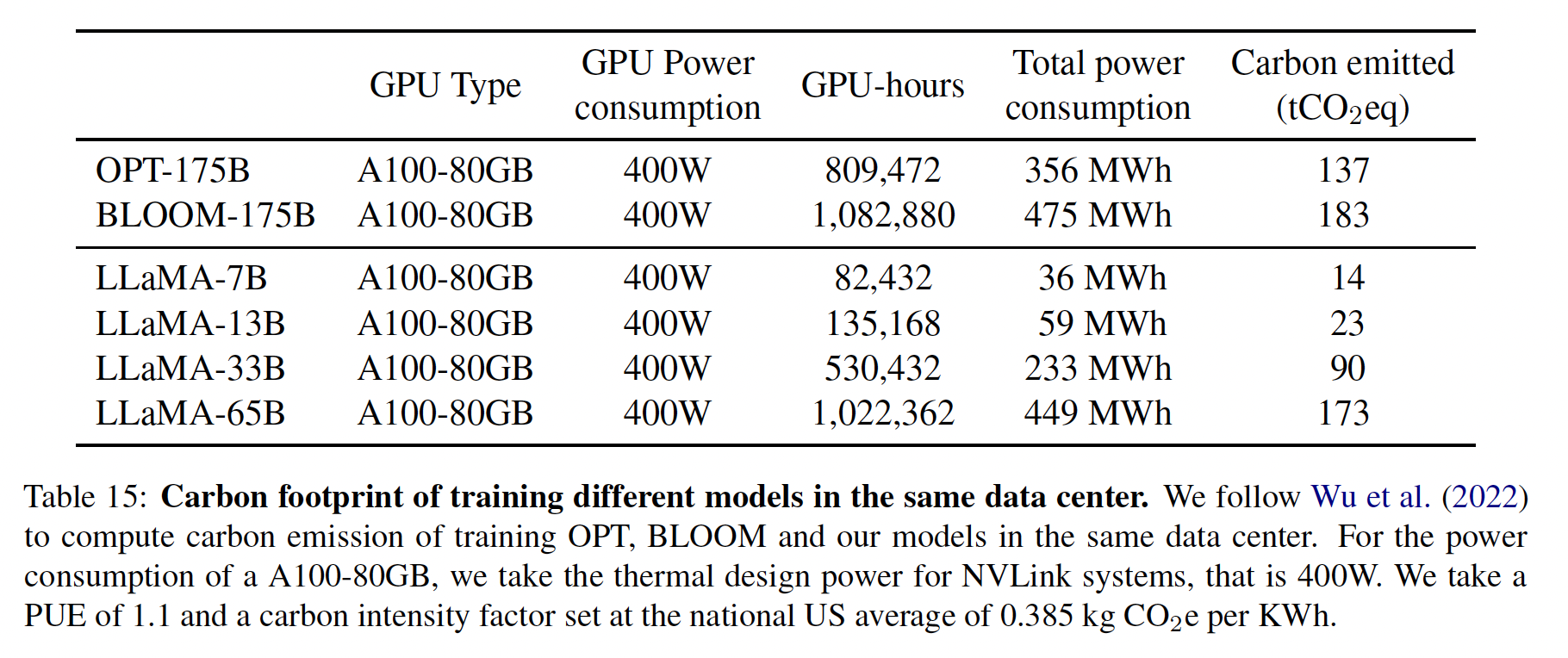
我们的模型训练消耗了大量的能源,造成了二氧化碳的排放。我们遵循最近关于这个问题的文献,在下表中对总的能源消耗和由此产生的碳足迹(
carbon footprint)进行了细分。我们遵从《Sustainable ai: Environmental implications,challenges and opportunities》的公式来估计训练一个模型所需的瓦特小时(Wh)以及碳排放量(tCO2eq)。对于
Wh,我们使用公式:其中:我们设置电力使用效率(
Power Usage Effectiveness: PUE)为1.1。碳排放的结果取决于用于训练网络的数据中心的位置。例如:
BLOOM使用的电网排放0.057 kg CO2eq/KWh,导致27吨二氧化碳当量(tCO2eq)。OPT使用的电网排放0.231 kg CO2eq/KWh,导致82吨二氧化碳当量。
在这项研究中,我们感兴趣的是比较这些模型在同一数据中心训练时的碳排放成本。因此,我们不考虑数据中心的位置,而是使用美国全国平均碳强度系数
0.385 kg CO2eq/KWh。这导致了以下的吨碳排放公式:为了公平比较,我们对
OPT和BLOOM采用同样的公式。对于OPT,我们假设训练需要在992个A100-80GB上进行34天(见其训练日志)。最后,我们估计我们使用了2048个A100-80GB在大约5个月的时间来开发我们的模型。这意味着,根据我们的假设,开发这些模型将花费大约2638 MWh,总排放量为1015吨二氧化碳当量。我们希望发布这些模型将有助于减少未来的碳排放,因为训练工作已经完成,而且一些模型相对较小,可以在单个GPU上运行。
45.6 附录
我们展示了一些用
LLaMA-65B获得的generations的例子(没有指令微调)。prompt用粗体字表示。


这里我们展示了几个
LLaMA-I的generation的例子,即用《Scaling instruction-finetuned language models》的协议和指令数据集微调的LLaMA-65B。





四十六、GLM[2021]
在未标记文本上预训练的语言模型大大推进了各种
NLP任务的SOTA,从自然语言理解(natural language understanding: NLU)到文本生成。在过去的几年里,下游的任务表现以及参数的规模也不断增加。一般来说,现有的预训练框架可以分为三个系列:自回归模型、自编码模型、
encoder-decoder模型。自回归模型(如
GPT)学习从左到右的语言模型。虽然它们在长文本generation中获得了成功,并且在扩展到数十亿个参数时表现出few-shot learning能力,但其固有的缺点是单向注意力机制,不能完全捕捉NLU任务中上下文单词之间的依赖关系。自编码模型(如
BERT),通过denoising objective(如Masked Language Model: MLM)学习双向上下文编码器。编码器产生适合自然语言理解任务的contextualized representation,但不能直接应用于文本生成。encoder-decoder模型对编码器采用双向注意力,对解码器采用单向注意力,并在它们之间采用交叉注意力(cross attention)。encoder-decoder模型通常被部署在条件生成(conditional generation)任务中,如text summarization和response generation。
T5通过encoder-decoder模型统一了NLU和conditional generation,但需要更多的参数来匹敌BRET-based模型(如RoBERTa、DeBERTa)的性能。这些预训练框架都不够灵活,无法在所有的
NLP任务中发挥竞争性。以前的工作试图通过多任务学习将各个框架的objective结合起来,从而统一不同的框架。然而,由于autoencoding objective和autoregressive objective的性质不同,简单的unification不能完全继承两个框架的优势。在论文
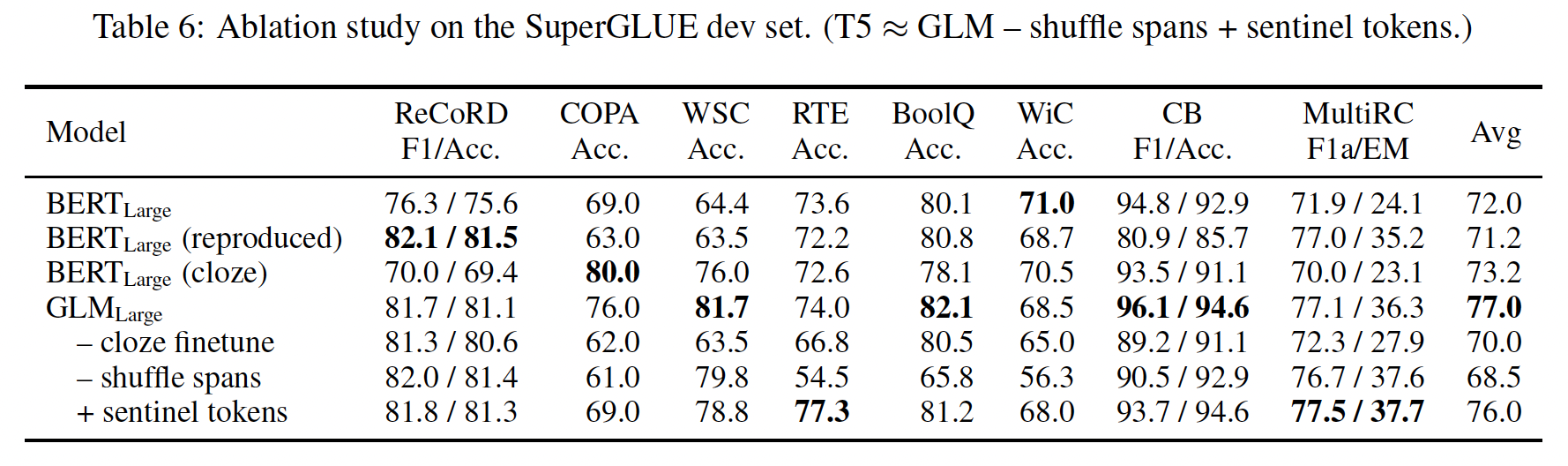
《GLM: General Language Model Pretraining with Autoregressive Blank Infilling》中,作者提出了一个名为General Language Model: GLM的预训练框架,基于自回归的填空(autoregressive blank infilling)。作者遵从自编码的思路,从输入文本中随机地blank出continuous span的token,并遵从自回归预训练的思路,训练模型来依次重建这些span(如下图所示)。虽然blanking filling已经在T5中用于text-to-text的预训练,但作者提出两项改进,即span shuffling和2D positional encoding。经验表明,在参数数量和计算成本相同的情况下,GLM在SuperGLUE benchmark上以4.6%-5.0%的较大优势明显优于BERT,并且在对类似大小的语料库(158GB)进行预训练时,GLM优于RoBERTa和BART。在NLU和文本生成任务上,具有较少参数和数据的GLM也明显优于T5。GLM的整体思路和T5相同,只是在技术细节上有一点点差异。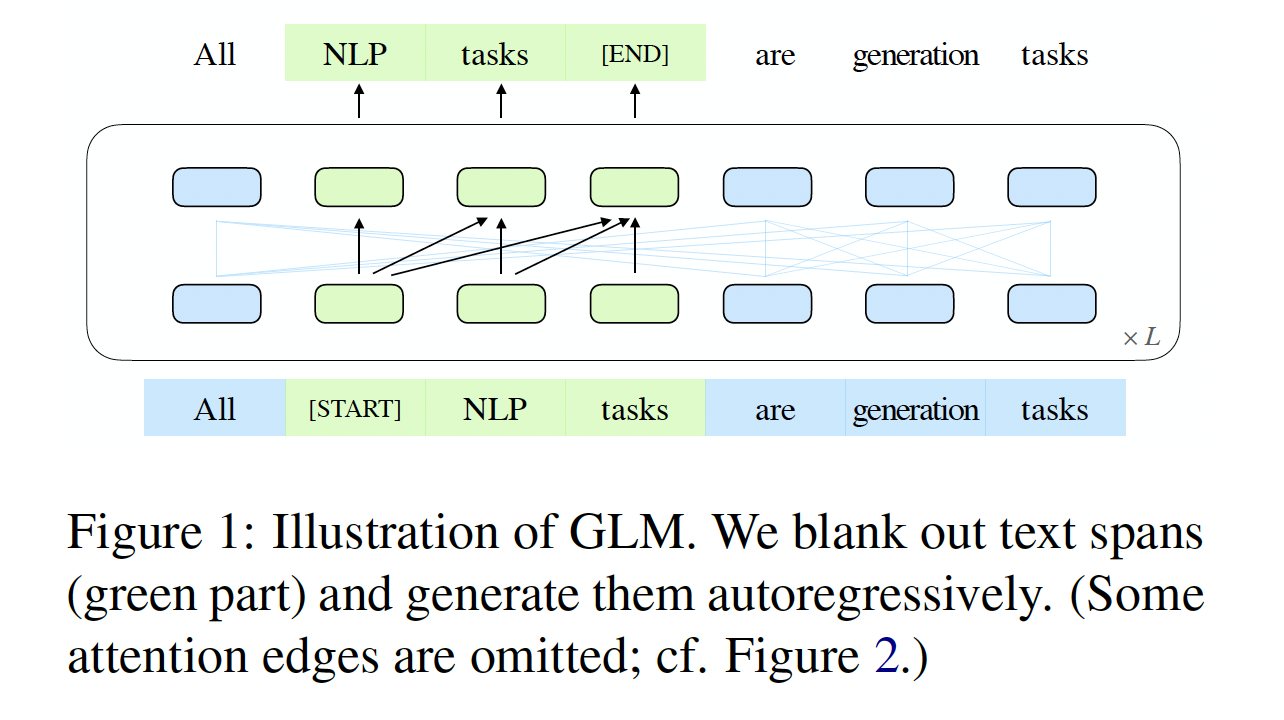
受
Pattern-Exploiting Training: PET(《Exploiting Cloze Questions for Few Shot Text Classification and Natural Language Inference》)的启发,作者将NLU任务重新表述为模仿人类语言的手工制作的完形填空问题。与PET所使用的BERT-based模型不同,GLM可以通过自回归的填空自然地处理对完形填空问题的multi-token answer。此外,作者表明,通过改变
missing span的数量和长度,autoregressive blank filling objective可以为conditional generation和unconditional generation预训练语言模型。通过对不同预训练目标的多任务学习,单个GLM可以在NLU和(conditional and unconditional)文本生成方面表现出色。根据经验,与standalone baseline相比,通过参数共享,具有多任务预训练的GLM在NLU、conditional text generation、以及语言建模任务中都取得了改进。相关工作:
Pretrained Language Model:预训练大型语言模型可以显著提高下游任务的性能。有三种类型的预训练模型:首先,自编码模型(
autoencoding model)通过denoising objective学习bidirectional contextualized encoder,用于自然语言理解。第二,自回归模型是通过从左到右的
language modeling objective来训练的。第三,
encoder-decoder model针对sequence-to-sequence的任务来预训练。
在
encoder-decoder model中,BART通过向编码器和解码器输入相同的输入,并采取解码器的final hidden states来进行NLU任务。相反,T5在text-to-text框架中公式化了大多数语言任务。然而,这两个模型都需要更多的参数来超越自编码模型(如RoBERTa)。UniLM将三种预训练模型统一在具有不同attention mask的masked language modeling objective下。NLU as Generation:先前,pretrained language model通过在learned representation上的线性分类器完成NLU的分类任务。GPT-2和GPT-3表明,给定任务指令(task instruction)或一些标记样本,生成式语言模型可以通过直接预测正确答案而不进行微调来完成NLU任务(如,问答任务)。然而,由于单向注意力的限制,生成式模型需要更多的参数来工作。最近,
PET(《Exploiting Cloze Questions for Few Shot Text Classification and Natural Language Inference》、《It’s Not Just Size That Matters: Small Language Models Are Also Few-Shot Learners》)提出,在few-shot setting中,将输入的样本重新表述为具有与pretraining corpus模式相同的完形填空问题。研究表明,与基于梯度的微调相结合,PET在few-shot setting中可以达到比GPT-3更好的性能,而只需要0.1%的参数。同样地,《Augmented natural language for generative sequence labeling》和《Structured Prediction as Translation between Augmented Natural Languages》将结构化的prediction task(如序列标注和关系提取),转换为sequence generation task。Blank Language Modeling:《Enabling language models to fill in the blanks》、《Blank language models》也研究blanking infilling模型。与他们的工作不同,我们预训练具有blank infilling objective的语言模型,并评估它们在下游NLU和generation任务中的表现。
46.1 模型
46.1.1 Autoregressive Blank Infilling
GLM是通过autoregressive blank infilling objective来训练的。给定一个输入文本text spanspantoken的一个序列spantoken长度。每个span被替换为单个[MASK] token,从而形成了一个corrupted textcorrupted text中的missing tokens,这意味着在预测span中的missing tokens时,该模型可以访问corrupted text和前面predicted spans。这意味着在预测期间,解码器不知道当前的
[MASK] token需要被解码为几个token。为了充分捕获不同
span之间的相互依赖关系,我们随机排列span的顺序,类似于permutation language model(如XLNet)。正式地,给定长度为span的数量。令spanspan序列。则我们定义预训练目标为:我们总是按照从左到右的顺序生成每个
blank中的token,也就是说,生成span其中:
span中位于token序列。span的第token。我们通过以下技术实现
autoregressive blank infilling objective。输入Part A是corrupted textPart B由masked span组成。Part A的token可以相互关注,但不能关注Part B的任何token。Part B的token可以关注Part A的所有token、以及Part B的前序token,但不能关注Part B的任何后续token。
这是借鉴了
UniLM的思想。为了开启
autoregressive generation,每个span都被填充了special token,即[START](记做[S])和[END](记做[E]),分别用于输入和输出。通过这种方式,我们的模型在一个统一的模型中自动学习双向编码器(用于Part A)和单向解码器(用于Part B)。下图说明了GLM的实现。我们从
span长度。我们反复采样新的span,直到至少有15%的原始token被掩码。根据经验,我们发现15%的比例对于下游NLU任务的良好表现至关重要。下图中,
(a)为原始输入序列,然后在(b)中被拆分为Part A和PartB。在(c)中,Part B中的两个span被随机混洗然后拼接到Part A之后,模型需要预测的是Part B位置上的输出。
46.1.2 多任务预训练
在前面的内容中,
GLM掩码了short span,适用于NLU任务。然而,我们对预训练一个能同时处理NLU和文本生成任务的单一模型感兴趣。然后,我们研究了一个多任务预训练的setup,该setup共同优化生成较长文本的第二个objective、以及blank infilling objective。我们考虑以下两个目标:document-level:我们采样一个span,其长度从原始输入文本长度的50%-100%的均匀分布中抽取。该目标旨在生成长文本。sentence-level:我们限制masked span必须是完整的句子。我们采样多个span(每个span也是一个完整的句子)以覆盖15%的原始token。这个目标是针对seq2seq任务,其预测往往是完整的句子或段落。
这两个新目标的定义与
blank infilling objective相同,唯一的区别是span的数量和span的长度。blank infilling objective采样多个span,平均span长度最短;document-level采样一个span,span长度最长;sentence-level采样多个span,平均span长度适中。然而,这三个目标的样本混合比例如何?论文并未说明。
46.1.3 模型架构
GLM使用单个Transformer,并对架构进行了一些修改:我们重新调整了
layer normalization和残差连接的顺序,这已被证明对大规模语言模型避免数值错误至关重要(《Megatron-lm: Training multi-billion parameter language models using model parallelism》)。我们使用单个的线性层用于
output token prediction。我们用
GeLU替换ReLU激活函数。Gaussian Error Linear Unit: GeLU激活函数:其中:
erf(x)为高斯误差函数
46.1.4 2D Positional Encoding
autoregressive blank infilling任务的挑战之一是如何对位置信息进行编码。Transformer依靠positional encoding来注入token的绝对位置和相对位置。我们提出了2D positional encoding来应对这一挑战。具体来说,每个token都有两组positional id来编码:第一组
positional id代表在corrupted textmasked span,它是相应的[MASK] token的位置。如
Figure 2 (c)所示:Part A中每个token的positional id依次递增。Part B中每个token的positional id等于该masked span在Part A中相应[MASK] token的positional id。这使得模型能够区分不同masked span的内容(在Part B中)和它的原始位置(在Part A中)。
第二组
positional id代表masked span内的位置。对于
Part A的token,它们的第二组positional id是0。因为
Part A不包含masked span的内容。对于
Part B的token,它们的第二组positional id的范围是从1到span length。
这两个
positional id通过learnable embedding table被投影到两个embedding向量中,这两个embedding向量然后都被添加到input token embedding中。
我们的编码方法确保了模型在重构
span时不知道masked span的长度。与其他模型相比,这是一个重要的区别。例如,XLNet对原始位置进行编码,使得模型能够感知到missing token的数量,SpanBERT用多个[MASK] token替换span,并保持token序列长度不变。我们的设计适合下游任务,因为通常generated text的长度事先是未知的。
46.1.5 微调 GLM
微调
GLM:通常,对于下游的
NLU任务,pretrained model产生的token representation馈入一个线性分类器,并预测出正确的label。这种做法与generative pretraining任务不同,导致预训练和微调之间的不一致。相反,我们遵从
PET(《Exploiting Cloze Questions for Few Shot Text Classification and Natural Language Inference》),将NLU分类任务重新表述为blank infilling的生成任务。具体来说,给定一个标记样本mask token,并且是用自然语言编写的从而代表任务的语义。例如,一个情感分类任务可以被表述为"SENTENCE}. It’s really [MASK]"。候选标签verbalizer"positive"和"negative"被映射到单词"good"和"bad"上。给定其中:
label set。因此,句子是
positive或negative的概率与blank处预测"good"或"bad"的概率成正比。然后我们用交叉熵损失对GLM进行微调(如下图所示)。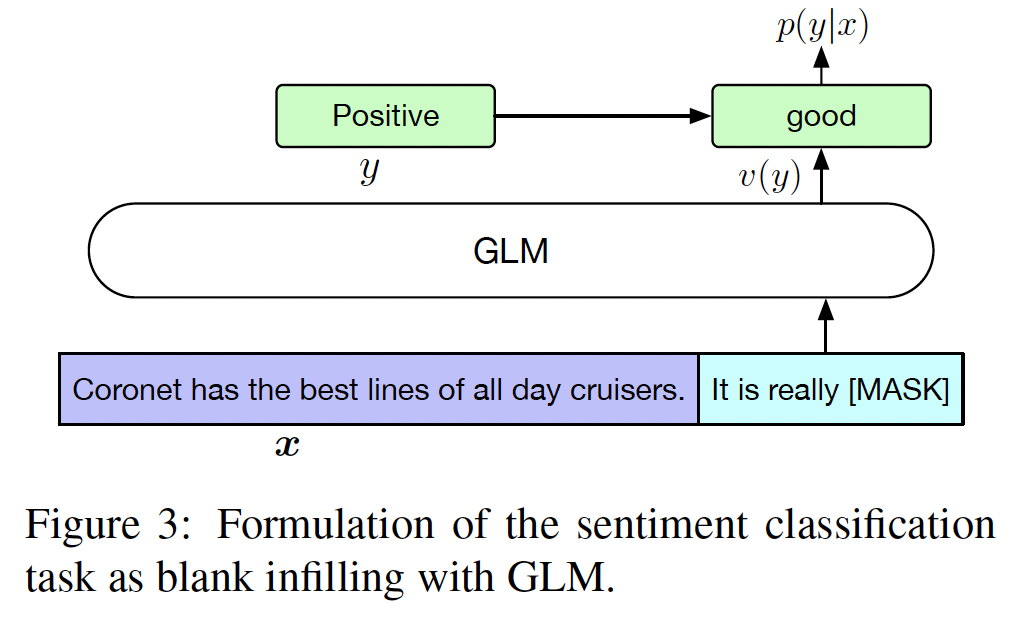
对于文本生成任务,给定的上下文构成了输入的
Part A,并在上下文最后附加了一个mask token。该模型以自回归方式生成Part B的文本。我们可以直接将pretrained GLM用于无条件生成任务,或者在下游的条件生成任务中对其进行微调。
46.1.6 讨论和分析
这里我们讨论了
GLM和其它预训练模型的差异。我们主要关注的是如何将它们适应于下游的blank infilling任务。与
BERT的比较:正如
XLNet所指出的,由于MLM的独立性假设,BERT无法捕获到masked token之间的相互依赖性。BERT的另一个缺点是,它不能正确填充multiple token的blank。为了推断长度为BERT需要连续进行BERT需要根据长度来改变[MASK] token的数量。
与
XLNet的比较:GLM和XLNet都是用自回归目标进行预训练的,但它们之间有两个区别:首先,
XLNet在corruption前使用original position encoding。在推理过程中,我们需要知道或枚举出答案的长度,这与BERT的问题相同。第二,
XLNet使用了双流的自注意力机制,而不是right-shift,以避免Transformer内部的信息泄露。这使预训练的时间成本增加了一倍。
与
T5的比较:T5提出了一个类似的blank infilling objective来预训练一个encoder-decoder Transformer。T5对编码器和解码器使用独立的positional encoding,并依靠多个哨兵token来区分masked span。在下游任务中,只使用其中一个哨兵token,导致模型容量的浪费、以及预训练与微调之间的不一致。UniLM和GLM在编码器和解码器之间共享了同一组positional embedding。此外,
T5总是以固定的从左到右的顺序(即,单向地)预测span。因此,如实验部分所述,GLM可以在参数和数据较少的情况下在NLU和seq2seq任务中明显优于T5。相比之下,
GLM采用了类似于XLNet的随机混洗策略,混洗了多个span的顺序。与
UniLM的比较:UniLM在自编码框架下,通过在双向注意力、单向注意力、以及交叉注意力中改变attention mask,结合了不同的预训练目标。然而,UniLM总是用[MASK] tokens替换masked span,这限制了它针对masked span及其上下文之间的依赖关系的建模能力。GLM输入前一个token并自动生成next token。"
UniLM总是用[MASK] tokens替换masked span,这限制了它针对masked span及其上下文之间的依赖关系的建模能力",这个结论从何而来?论文并未说明。在下游的生成任务上对
UniLM进行微调,也依赖于masked language modeling,其效率较低。UniLMv2对生成任务采用partially auto-regressive modeling,同时对NLU任务采用auto-encoding objective。相反,GLM通过自回归预训练将NLU任务和生成任务统一起来。
46.2 实验
46.2.1 预训练配置
为了与
BERT进行公平的比较,我们使用BooksCorpus和English Wikipedia作为我们的预训练数据。我们使用BERT的uncased wordpiece tokenizer,词表规模为30k。我们用与BERT_Base和BERT_Large相同的架构训练GLM_Base和GLM_Large,分别包含110M和340M的参数。对于多任务预训练,我们用
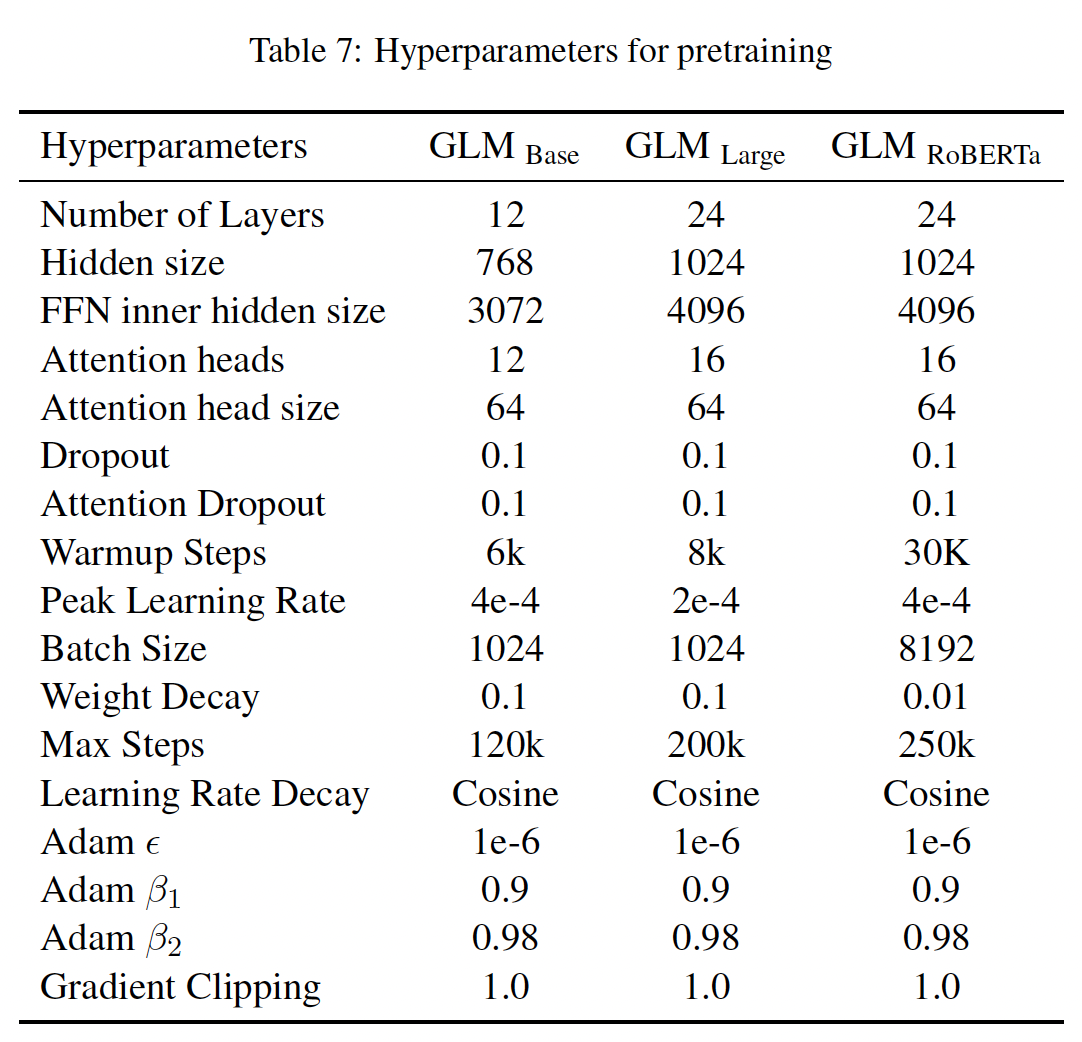
blank infilling objective和document-level or sentencelevel objective的混合来训练两个大模型,分别表示为GLM_Doc和GLM_Sent。此外,我们还用document_level多任务预训练来训练了两个较大的GLM模型,参数分别为410M(30层,隐层大小1024,16个attention head)和515M(30层,隐层大小1152,18个attention head)参数的 ,分别表示为GLM_410M和GLM_515M。为了与
SOTA模型进行比较,我们还用与RoBERTa相同的数据、tokenization、超参数训练了一个大模型,表示为GLM_RoBERTa。由于资源限制,我们只对模型进行了250k步的预训练,这 是RoBERTa和BART训练步数的一半,在trained token数量上接近T5。预训练数据集:
GLM_Base, GLM_Large在与BERT相同的BooksCorpus和English Wikipedia上预训练。GLM_RoBERTa的预训练数据参考RoBERTa,其中RoBERTa在BookCorups、Wikipedia、CC-News、OpenWebText、Stories上预训练。Stories数据集已经不再提供,因此我们删除了Stories数据集。此外,我们用
OpenWebText2代替了OpenWebText。CC-News数据集已经不再公开,我们用CC-News-en来代替。
所有使用的数据集共有
158GB的未压缩文本,与RoBERTa的160GB数据集大小接近。
超参数(如下表所示):
GLM_Base和GLM_Large的超参数与BERT使用的超参数相似,从而用于公平地比较。GLM_Doc和GLM_Sent的超参数与GLM_Large的超参数相同。除了
GLM_410M和GLM_515M的Transformer架构外,其他的超参数与GLM_Large相同。
这些模型在
64个V100 GPU上进行了200K步的训练,batch_size = 1024,最大序列长度为512,这对GLM_Large来说需要大约2.5天。为了训练GLM_RoBERTa,我们遵循RoBERTa的大部分超参数。主要的区别包括:由于资源的限制,我们只对
GLM_RoBERTa进行了250k步的预训练,这是RoBERTa和BART训练步数的一半,在trained tokens数量上接近T5。我们使用余弦衰减而不是线性衰减来调度学习率。
我们额外应用了值为
1.0的梯度剪裁。
我们的实现基于
Megatron-LM和DeepSpeed。
46.2.2 实验结果
为了评估我们
pretrained GLM模型,我们在SuperGLUE基准上进行了实验,并报告了标准的指标。我们按照PET的方法,将分类任务重新表述为用人类精心设计的完形填空问题,如下表所示,其中ReCoRD, COPA, WSC的答案可能包含多个token, 而其它任务的答案仅包含一个token。 然后,如前所述,我们在每个任务上微调pretrained GLM模型。
为了与
GLM_Base和GLM_Large进行公平的比较,我们选择BERT_Base和BERT_Large作为我们的baseline,它们在相同的语料库上进行了预训练,并且训练时间相近。为了与
GLM_RoBERTa进行比较,我们选择T5, BART_Large, RoBERTa_Large作为我们的baseline。T5在参数数量上与BERT_Large没有直接的匹配,所以我们同时展示了T5_Base(220M参数)和T5_Large(770M参数)的结果。所有其他baseline的规模都与BERT_Large相似。实验结果如下表所示:
在相同数量的训练数据下,
GLM在大多数任务中的base或large架构上都一直优于BERT。唯一的例外是WiC。平均而言,GLM_Base的得分比BERT_Base高4.6%,GLM_Large的得分比BERT_Large高5.0%。这清楚地表明了我们的方法在NLU任务中的优势。在
RoBERTa_Large的设置中,GLM_RoBERTa仍然可以实现对baseline的改进,但幅度较小。具体来说,GLM_RoBERTa优于T5_Large,但规模只有其一半。我们还发现,
BART在具有挑战性的SuperGLUE基准上表现不佳。我们猜测这可能是由于encoder-decoder架构的低的parameter efficiency和denoising sequence-to-sequence objective造成的。
多任务预训练:然后我们评估
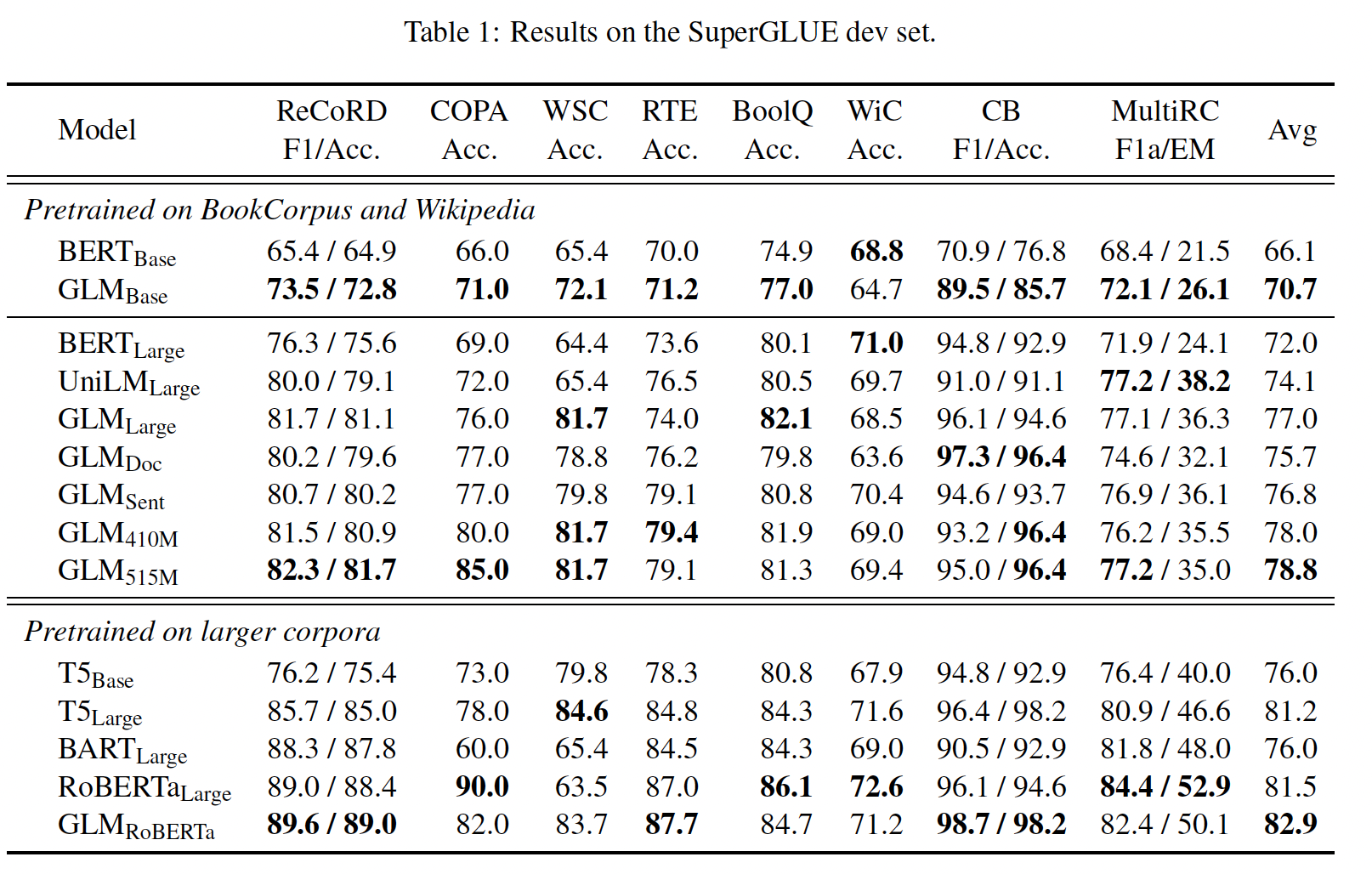
GLM在多任务设置中的表现。在一个training batch中,我们以相同的机会对short span和longer span(document-level或sentence-level)进行采样。我们对多任务模型进行评估,包括NLU、seq2seq、blank infilling和zero-shot language modeling。SuperGLUE:对于NLU任务,我们在SuperGLUE基准上评估模型。结果如Table 1所示。我们观察到:在多任务预训练中,
GLM_Doc和GLM_Sent的表现比GLM_Large略差,但仍然优于BERT_Large和UniLM_Large。在多任务模型中,
GLM_Sent的表现平均比GLM_Doc好1.1%。将
GLM_Doc的参数增加到410M(1.25倍的BERT_Large)会导致比GLM_Large更好的性能。515M参数的GLM(1.5倍的BERT_Large),性能甚至更好。
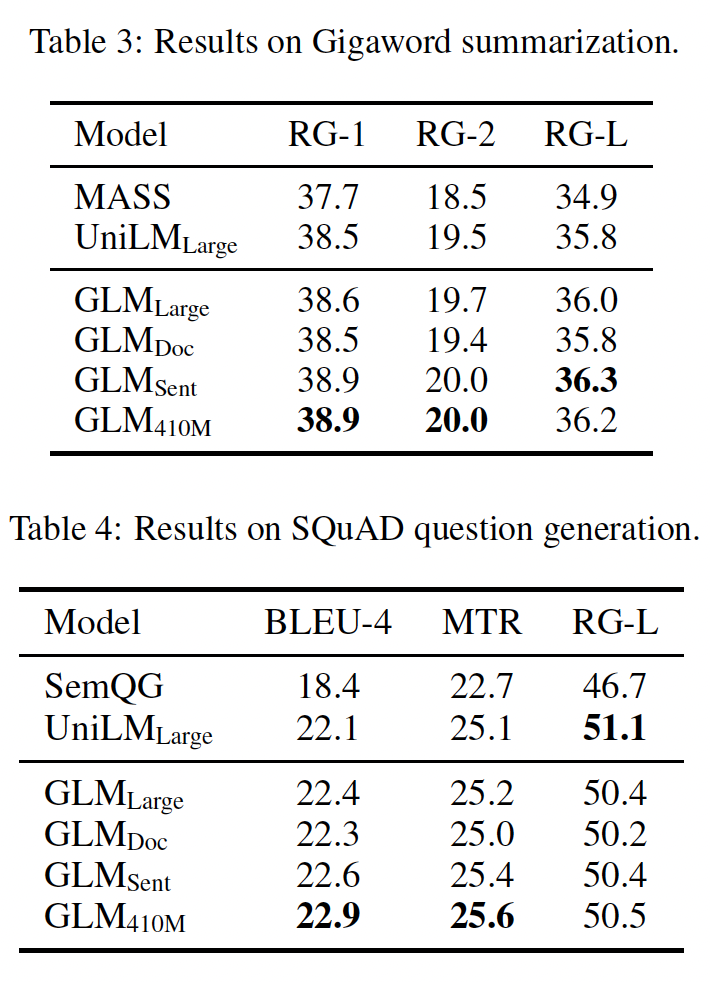
Sequence-to-Sequence:考虑到现有的baseline结果,我们使用Gigaword数据集进行abstractive summarization、以及SQuAD 1.1数据集进行question generation,作为在BookCorpus和Wikipedia上预训练好的模型的基准。此外,我们使用CNN/DailyMail和XSum数据集进行abstractive summarization,作为在较大语料库上预训练好的模型的基准。Table 3和Table 4显示了在BookCorpus和Wikipedia上训练的模型的结果。我们观察到:GLM_Large可以在这两个生成任务上实现与其他预训练模型相匹配的性能。GLM_Sent可以比GLM_Large表现得更好,而GLM_Doc的表现比GLM_Large略差。这表明document-level objective,即教会模型扩展给定的上下文,对conditional generation的帮助较小,而conditional generation的目的是从上下文中提取有用信息。将
GLM_Doc的参数增加到410M,可以在这两项任务上获得最佳性能。
在较大的语料库上训练的模型的结果见
Table 2。GLM_RoBERTa可以达到与seq2seq BART模型相匹配的性能,并且超过了T5和UniLMv2。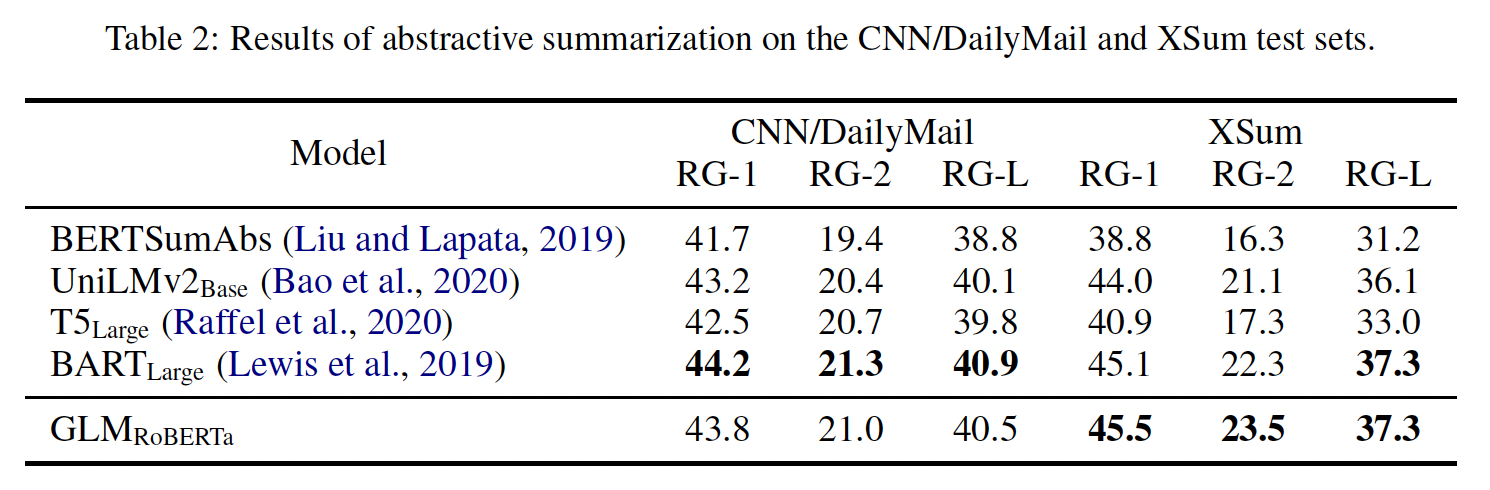
Text Infilling:text infilling是预测与周围上下文一致的missing spans of text的任务。GLM是用autoregressive blank infilling objective训练的,因此可以直接解决这个任务。我们在Yahoo Answers数据集上评估了GLM,并与Blank Language Model: BLM进行了比较,后者是专门为text infilling设计的模型。从下表的结果来看,GLM以较大的优势(1.3 ~ 3.9 BLEU)超过了以前的方法,在这个数据集上取得了SOTA的结果。我们注意到,GLM_Doc的表现略逊于GLM_Large,这与我们在seq2seq实验中的观察结果一致。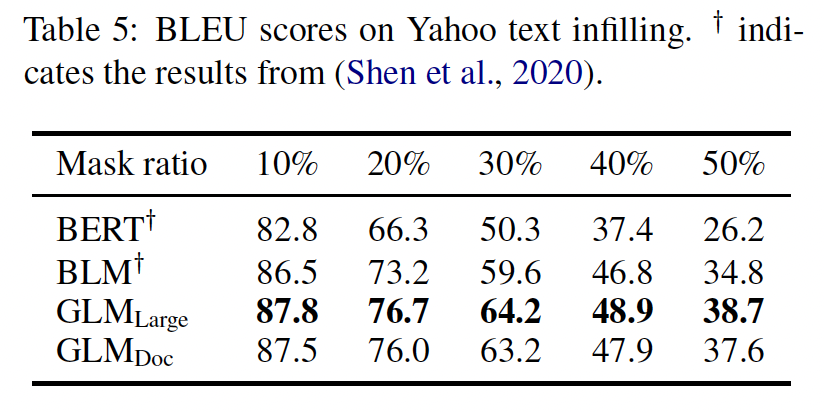
Language Modeling:大多数语言建模数据集(如WikiText103) ,是由维基百科文档构建的,我们的预训练数据集已经包含了这些文档。因此,我们在预训练数据集的一个held-out测试集上评估语言建模的困惑度,该测试集包含大约20M个token,记做BookWiki。我们还在LAMBADA数据集上评估了GLM,该数据集测试了系统对文本中长距离依赖关系的建模能力。其任务是预测一段话的最后一个单词。作为baseline,我们用与GLM_Large相同的数据和tokenization来训练一个GPT_Large模型。所有的模型都是在
zero-shot setting中进行评估的。由于GLM学习的是双向注意,我们也在上下文被双向注意力编码的情况下评估GLM。结果如下图所示。在预训练期间没有
generative objective,GLM_Large不能完成语言建模任务,困惑度大于100(未在图中标识)。在参数数量相同的情况下,
GLM_Doc的表现比GPT_Large差。这是预期的,因为GLM_Doc也优化了blank infilling objective。将模型的参数增加到
410M(1.25倍的GPT_Large)导致性能接近于GPT_Large。GLM_515M(1.5倍的GPT_Large)可以进一步超越GPT_Large。
在参数数量相同的情况下,用双向注意力对上下文进行编码可以提高语言建模的性能。在这种设定下,
GLM_410M的性能超过了GPT_Large。这就是GLM相对于单向GPT的优势。我们还研究了2D positional encoding对long text generation的贡献。我们发现,去除了2D positional encoding会导致语言建模的准确率降低和困惑度的提高。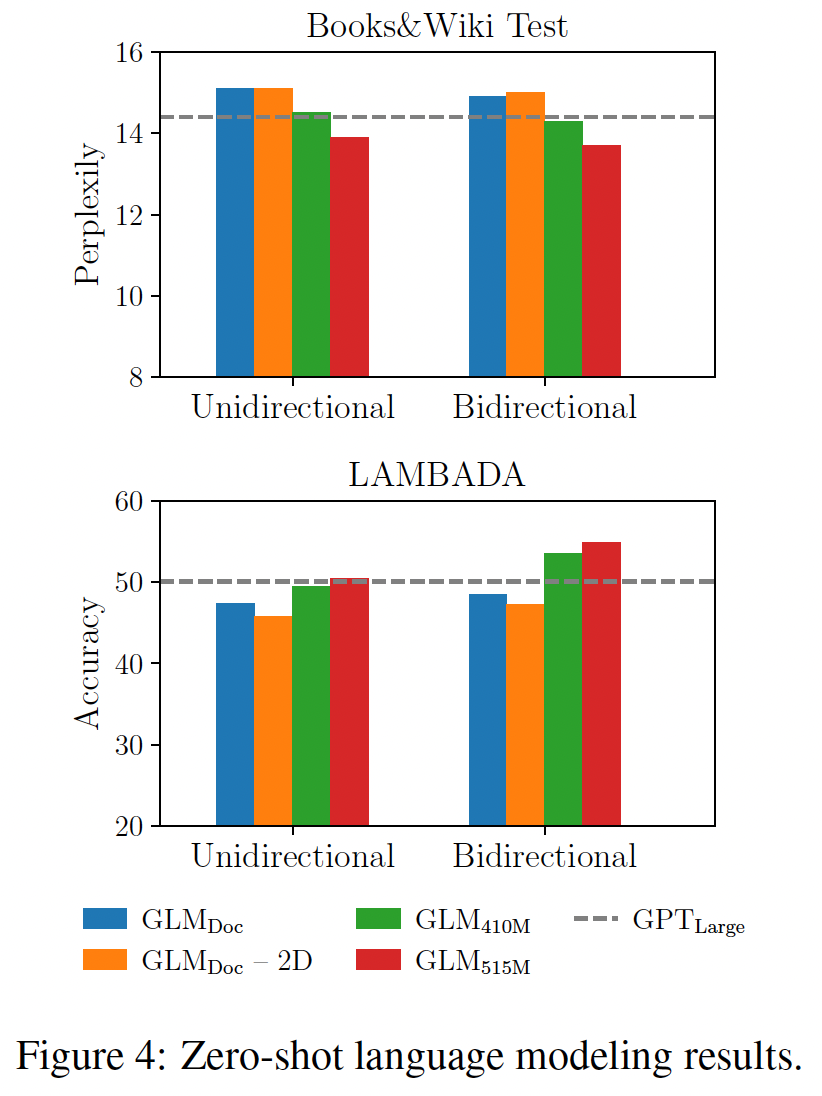
总结:最重要的是,我们得出结论,
GLM在自然语言理解任务、以及文本生成任务中有效地共享模型参数,从而比独立的BERT、encoder-decoder或GPT模型取得更好的性能。消融研究:下表显示了我们对
GLM的消融分析。首先,为了提供一个与
BERT的公平地比较,我们用我们的实现、数据、超参数训练一个BERT_Large模型(表中第二行,BERT_Large(reproduced))。其性能比官方的BERT_Large略差,比GLM_Large明显差。它证实了GLM在NLU任务上比Masked LM预训练的优越性。其次,我们展示了作为
sequence classifier微调的GLM在SuperGLUE性能(第5行)和具有cloze-style微调的BERT(第3行)。与cloze-style微调的BERT相比,GLM得益于自回归预训练。特别是在ReCoRD和WSC上,其中verbalizer由多个token组成,GLM一直优于BERT。这证明了GLM在处理可变长度的blank方面的优势。另一个观察结果是,在
NLU任务上,cloze formulation对于GLM的表现至关重要。对于大型模型,cloze-style的微调可以提高7个点的性能。最后,我们用不同的预训练设计来比较
GLM的变体,以了解其重要性。第
6行显示,移除shuffle span(总是从左到右预测masked span)会导致SuperGLUE的性能严重下降。第
7行使用不同的哨兵token,而不是单一的[MASK] token来代表不同的masked token。该模型的表现比标准GLM更差。我们假设,它浪费了一些建模能力来学习不同的哨兵token,而这些哨兵token在只有一个blank的下游任务中没有使用。
在
Figure 4中,我们表明,移除2D positional encoding的第二维会损害long text generation的性能。我们注意到,
T5是以类似的blank infilling objective进行预训练的。GLM在三个方面有所不同:GLM由单个编码器组成;GLM对masked span进行混洗(混洗不同的masked span,而不是混洗masked span内部的token);GLM使用一个[MASK]而不是多个哨兵token。虽然由于训练数据和参数数量的不同,我们不能直接比较
GLM和T5,但Table 1和Table 6的结果已经证明了GLM的优势。