三十三、AFN [2020]
手工制作有用的交叉特征是昂贵的、耗时的,而且结果可能无法泛化到未见过的特征交互。为了解决这个问题,人们提出了
Factorization Machine: FM,通过将交叉特征的权重参数化为原始特征的embedding向量的内积从而显式地建模二阶交叉特征。为了更加通用,在最初的工作中还引入了涉及高阶特征组合的高阶FM(HOFM)。尽管有卓越的预测能力,但在
FM/HOFM中仍有两个关键问题需要回答:- 首先,我们应该考虑交叉特征的最大阶次是什么?虽然较大的阶次可以建模更复杂的特征交互,并且似乎是有益的,但交叉特征的数量会随着最高阶次的增加而呈指数级增长,从而导致高的计算复杂度。这限制了高阶交叉特征的实际使用。
- 其次,在最高阶数下有用的交叉特征集合是什么?必须认识到,并非所有的特征都包含针对估计目标的有用信号,不同的交叉特征通常具有不同的预测能力。不相关的特征之间的交互可以被认为是噪音,对预测没有贡献,甚至会降低模型的性能。
AFM通过用注意力分数来reweighing每个交叉特征来区分特征交互的重要性。然而,在复杂的特征组合上应用注意力机制会大大增加计算成本。因此,AFM旨在仅仅建模二阶的特征交互。
在论文
《Adaptive Factorization Network: Learning Adaptive-Order Feature Interactions》中,作者认为现有的因子分解方法未能适当地回答上述两个问题。通常而言,现有的因子分解方法是按照列举、以及过滤的方式来建模特征交互:首先定义最大阶次,然后枚举最大阶次以内的所有交叉特征,最后通过训练来过滤不相关的交叉特征。这个过程包括两个主要的缺点:- 首先,预设最大阶数(通常较小)限制了模型在寻找有
discriminative的交叉特征方面的潜力,因为要在表达能力和计算复杂性之间进行trade-off。 - 其次,考虑所有的交叉特征可能会引入噪音并降低预测性能,因为并非所有无用的交叉特征都能被成功过滤掉。
因此,论文
《Adaptive Factorization Network: Learning Adaptive-Order Feature Interactions》提出了Adaptive Factorization Network: AFN,从数据中自适应地学习任意阶次的交叉特征及其权重。其关键思想是:将feature embedding编码到一个对数空间中,并将特征的幂次转换为乘法。AFN的核心是一个对数神经转换层logarithmic neural transformation layer,由多个vector-wise对数神经元组成。每个对数神经元的目的是:在可能有用的特征组合中,自动学习特征的幂次(即,阶次)。在对数神经转换层上,AFN应用前馈神经网络来建模element-wise的特征交互。与FM/HOFM不同的是,AFN能够自适应地从数据中学习有用的交叉特征,而且最大阶次可以通过数据自动学到。论文主要贡献:
- 据作者所知,他们是第一个将对数转换结构与神经网络结合起来,从而建模任意阶次的特征交互。
- 基于所提出的对数转换层,作者提出了
AFN从而从数据中自适应地学习任意阶次的交叉特征及其权重。 - 作者表明:
FM/HOFM可以被解释为AFN的两种特例,并且AFN中学到的阶次允许在不同的交叉特征中rescaling feature embedding。 - 论文在四个公共数据集上进行了广泛的实验。结果表明:所学的交叉特征的阶次跨度很大;与
SOTA方法相比,AFN取得了卓越的预测性能。
33.1 背景
Feature Embedding:遵从传统,我们将每个输入样本表示为一个稀疏的向量:其中:
feature field的数量,feature field的representation,由于大多数
categorical features是稀疏的、高维的,一个常见的做法是将它们映射到低维潜空间中的稠密向量(即,embedding)。具体而言,一个categorical featureone-hot encoded vector,然后计算embedding向量其中
feature fieldembedding matrix。对于数值特征
representation是一个标量categorical feature之间的交互,其中:
fieldembedding vector(由该field内的所有特征取值所共享)。
最终我们得到
feature embedding集合FM或其他模型。FM:FM显式建模高维数据的二阶特征交互。从公式上看,FM的预测为:其中
直观地,第一项
feature embedding的pair-wise内积之和。此外,
Higher-Order Factorization Machine: HOFM用于捕获高阶的特征交互:其中:
feature embedding的element-wise的乘积之和。HOFM的时间复杂度为feature embedding的维度。由于计算复杂度高,HOFM很少被应用于真正的工业系统。FM和HOFM的一个共同局限性是:它们以相同的权重来建模所有的特征交互。由于并非所有的交叉特征都是有用的,纳入所有的交叉特征进行预测可能会引入噪音并降低模型性能。如前所述,一些方法致力于缓解这一问题:
AFM利用注意力机制为不同的交叉特征分配非均匀的权重,xDeepFM只为保留的交叉特征学习权重。然而,这些方法引入了额外的成本,并且在模型训练前仍被限制在一个预设的最大特征交互阶次discriminative的高阶交叉特征的机会。在本文中,我们建议从数据中自适应地学习任意阶交叉特征。最大阶次和交叉特征集合都将通过模型训练自适应地确定,从而在不牺牲预测能力的前提下实现高计算效率。
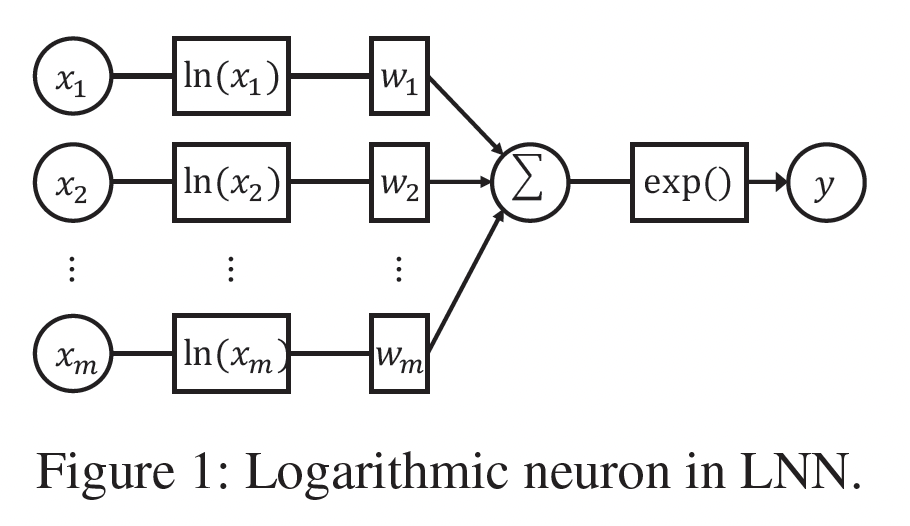
Logarithmic Neural Network: LNN:对数神经网络Logarithmic Neural Network最初是为了近似unbounded的非线性函数而提出的。LNN由多个对数神经元组成,其结构如下图所示。从形式上看,一个对数神经元可以表述为:LNN的理念是将输入转换到对数空间,将乘法转化为加法,除法转化为减法,幂次转化为乘法。尽管多层感知机(multi-layer perceptron: MLP)是众所周知的通用函数逼近器,但当输入无界时,它们在逼近某些函数如乘法、除法和幂次方面的能力有限。相反,LNN能够在整个输入范围内很好地逼近这些函数。在本文中,我们利用对数神经元来自适应地学习数据中交叉特征的每个
feature field的幂次。我们强调LNN和我们提出的AFN之间的三个关键区别:AFN学到的幂次被应用到vector-wise level,并且在相同field的所有feature embedding之间共享。我们模型的输入是待学习的
feature embedding。因此,我们需要使用一些技术来保持梯度稳定,并学习适当的feature embedding和combination。在
AFN中,我们在学到的交叉特征上进一步应用前馈隐层,以增强我们模型的表达能力。AFN有几个显著的缺点:- 要求
embedding为正数,这对模型施加了很强的约束。 - 由于大多数
embedding在零值附近,一个很微小的扰动(如计算精度导致的计算误差)就可能对模型产生影响,因此读者猜测模型难以训练。
- 要求
33.2 模型
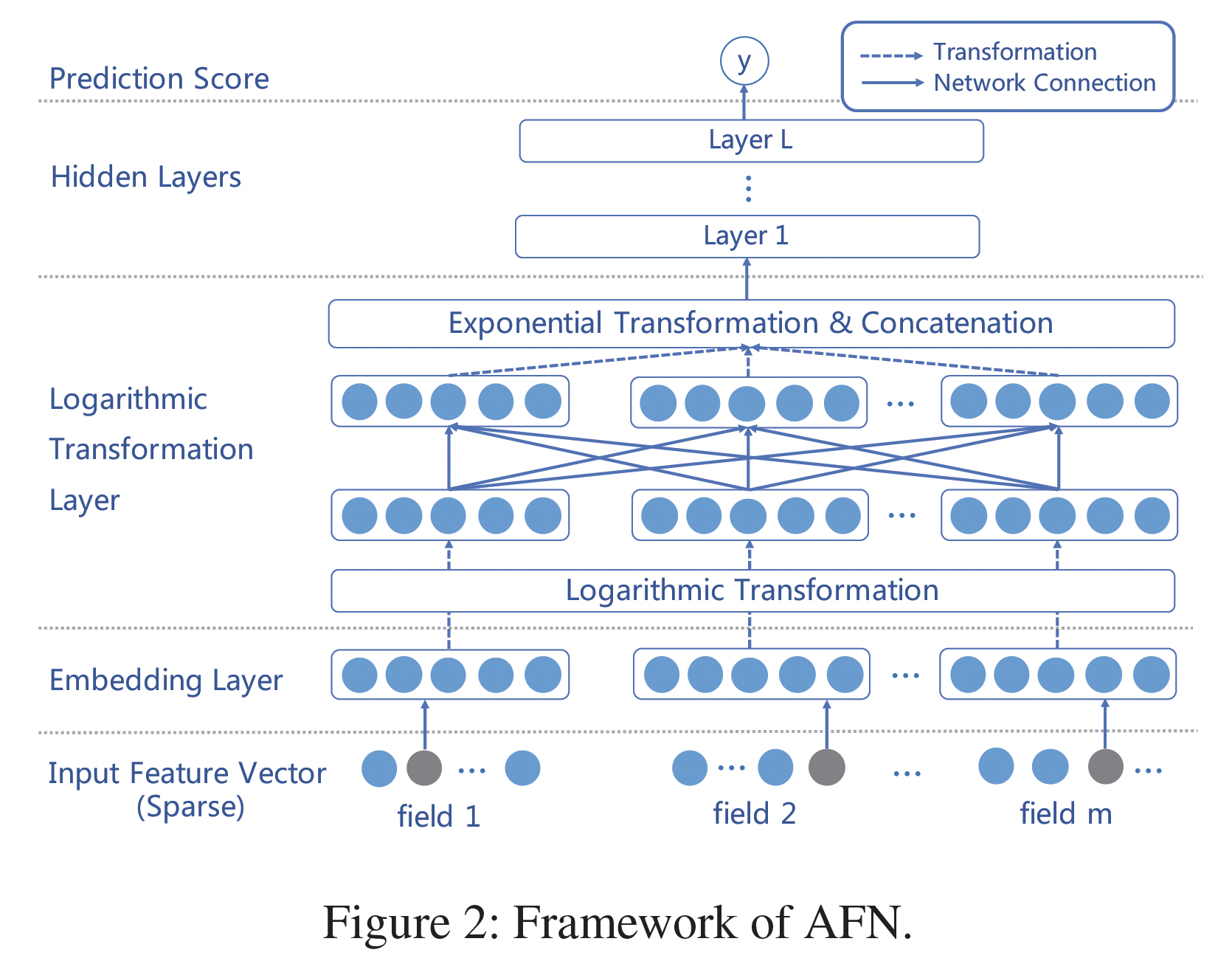
AFN的整体结构如下图所示。Input Layer and Embedding Layer:AFN的inpyt layer同时采用sparse categorical feature和numerical feature。如前所述,所有的原始输入特征首先被转换为共享潜在空间的embedding。这里我们介绍两个实现
embedding layer的关键技术:首先,由于我们将对后续的层中的
feature embedding进行对数转换,我们需要保持embedding中的所有数值为正数。如何确保
embedding中的所有数值都是正的?论文没有说明。此外,embedding非负,这对模型施加了一个很强的约束。然后,即使采用了非负的embedding,然后对于接近零的embedding,它的 “对数--指数” 变换非常敏感,一个很微小的扰动(如计算精度导致的计算误差)就可能对模型产生影响,因此读者猜测模型较难训练。其次,建议在
zero embedding中加入一个小的正值(如
最后,
embedding layer的输出是positive feature embedding的一个集合:Logarithmic Transformation Layer:AFN的核心是对数转换层logarithmic transformation layer,它学习交叉特征中每个feature field的幂(即阶次)。该层由多个vector-wise的对数神经元组成,第vector-wise对数神经元的输出为:其中:
feature field上的系数;element-wise的;对上式的主要观察是:每个对数神经元
feature field的二阶交叉特征。因此,我们可以使用多个对数神经元来获得任意阶次的不同feature combination作为该层的输出。注意,系数矩阵
0或1,其中Feed-forward Hidden Layers and Prediction:在对数转换层上,我们堆叠了几个全连接层从而组合所得到的交叉特征。我们首先将所有的交叉特征拼接起来作为前馈神经网络的输入:
其中:
然后我们将
其中:
最后,隐层的输出
其中:
prediction layer的权重向量和偏置。
Optimization:目标函数针对不同的任务(分类、回归、ranking)而做出相应的选择。常见的目标函数是对数损失:其中:
sigmoid函数。我们采用
Adam优化器进行随机梯度下降。此外,我们对logarithmic transformation、exponential transformation和所有隐层的输出进行batch normalization: BN。有两个原因:- 首先,
feature embeddingembedding往往涉及大的负值,并有显著的方差,这对后续几层的参数优化是有害的。由于BN可以缩放并shift输出为归一化的数值,因此它对AFN的训练过程至关重要。 - 其次,我们在对数转换层之后采用多层神经网络。对隐层的输出进行
BN有助于缓解协方差漂移问题,从而导致更快的收敛和更好的模型性能。
- 首先,
Ensemble AFN with DNN:之前的工作(Wide&Deep、DeepFM、xDeepFM)提出将基于交叉特征的模型(如FM)的预测结果与基于原始特征的神经方法的预测结果进行ensemble,以提高性能。类似地,我们也可以将AFN与深度神经网络进行结合。为了执行AFN和神经网络之间的ensemble,我们首先分别训练这两个模型。之后,我们建立一个ensemble模型来结合两个训练好的模型的预测结果:其中:
AFN和DNN的预测结果,ensemble model可以通过logloss损失来进行训练。我们把这个ensemble模型称为"AFN+"。我们的
ensemble方法与DeepFM使用的方法有些不同:DeepFM的feature embedding在FM和DNN之间共享,而我们将AFN和DNN的embedding layer分开从而避免干扰。主要的原因是:与DeepFM不同,AFN中的embedding value的分布应该始终保持positive,这和DNN中embedding value的分布相差甚远。众所周知,在
CTR预测任务中,DNN模型的参数主要集中在embedding table。这里用到了两套embedding table,模型参数翻倍。根据我们的实验,这种分离方法略微增加了模型的复杂性,但会带来更好的性能。
讨论:
理解
AFN中的阶次:AFN通过对数转换层学习交叉特征中每个特征的阶次。由于对数转换层的权重矩阵AFN学到的特征阶次,我们借鉴了field-aware factorization machine: FFM的一些思想。在
FFM中,每个特征都关联feature embedding,其中feature field的数量。FFM与FM的区别在于,每个特征在与不同field的其它特征进行交互时采用不同的embedding。FFM的启示是:要避免不同field的特征空间之间的干扰。 在AFN中,每个特征的阶次可以被看作是相应feature embedding的一个比例因子。例如,考虑一个取值从0到1之间的embedding,大于1的阶次会缩小embedding值,而小于1的阶次则扩大embedding值。通过与FFM的类比,当与不同field的其它特征进行交互时,可以利用AFN学到的阶次来rescale feature embedding。与
FM和HOFM的关系:我们首先表明,FM可以被看作是AFN的一个特例。根据公式feature embedding的幂次element-level上近似于一个简单的sum函数,那么AFN可以准确地恢复FM。类似地,当我们有足够多的对数神经元来提供最大阶次内的所有交叉特征,并允许隐层近似
sum函数时,AFN能够恢复HOFM。时间复杂度:令
feature embedding维度和feature field数量。在AFN中,对数神经元可以在AFN的总时间复杂度是至于
HOFM,假设HOFM的时间复杂度与交叉特征的最大阶次AFN中,由于其自适应的交叉特征生成方式,AFN的时间成本与CIN接近。
33.3 实验
数据集:
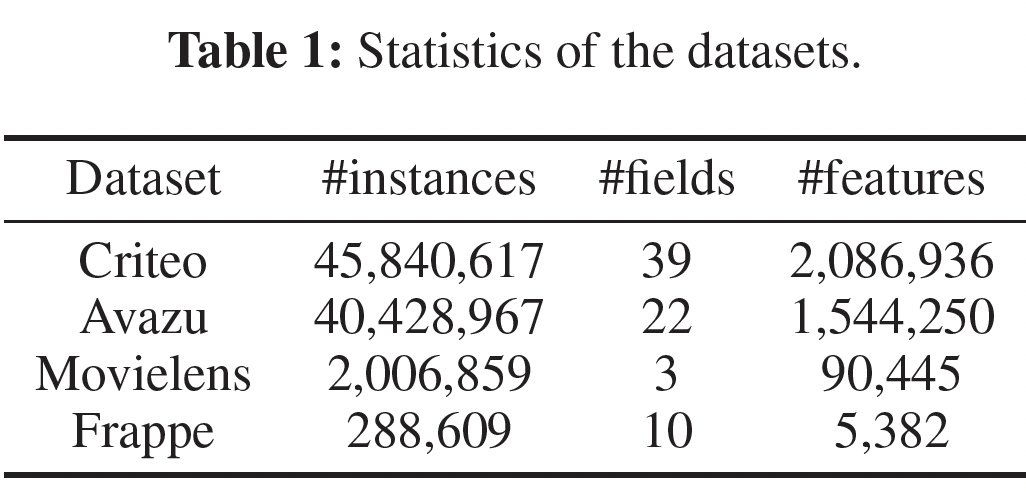
Criteo:包含13个数值特征和26个categorical feature。Avazu:包含22个feature field,包括用户特征和广告属性。Movielens:我们将每个tagging record((user ID, movie ID, tag)三元组)转换为一个特征向量来作为输入。target为:用户是否为电影分配了一个特定的tag。Frappe:我们将每条日志(user ID, app ID, context features)转换为一个特征向量来作为输入。target为:用户是否在上下文中使用过该app。
所有数据集的统计信息如下表所示。
评估指标:
AUC, Logloss。baseline方法:- 一阶方法(对原始特征进行线性相加):
Linear Regression: LR。 - 考虑二阶交叉特征的
FM-based方法:FM、AFM。 - 建模高阶特征交互的高级方法:
HOFM、NFM、PNN、CrossNet、CIN。 - 涉及
DNN作为组件的ensemble方法:Wide&Deep(为公平比较,我们省略了手工制作的交叉特征),DeepFM、Deep&Cross、xDeepFM。
- 一阶方法(对原始特征进行线性相加):
实现细节:
- 使用
Tensorflow实现、采用Adam优化器、学习率0.001、mini-batch size = 4096。 - 对于
Criteo/Avazu/Movielens/Frappe数据集,默认的对数神经元数量1500/1200/800/600。 AFN中默认使用3个隐层、每层400个神经元。- 为了避免过拟合,根据验证集的
AUC进行early-stopping。 - 在所有的模型中,我们将
feature embedding的维度设置为10。 - 我们对所有涉及
DNN的方法使用相同的神经网络结构(即3层:400-400-400)以进行公平的比较。 HOFM的最高阶次设为3。- 所有其他的超参数都是在验证集上调优的。
- 对于每个经验结果,我们运行实验
3次并报告平均值。
- 使用
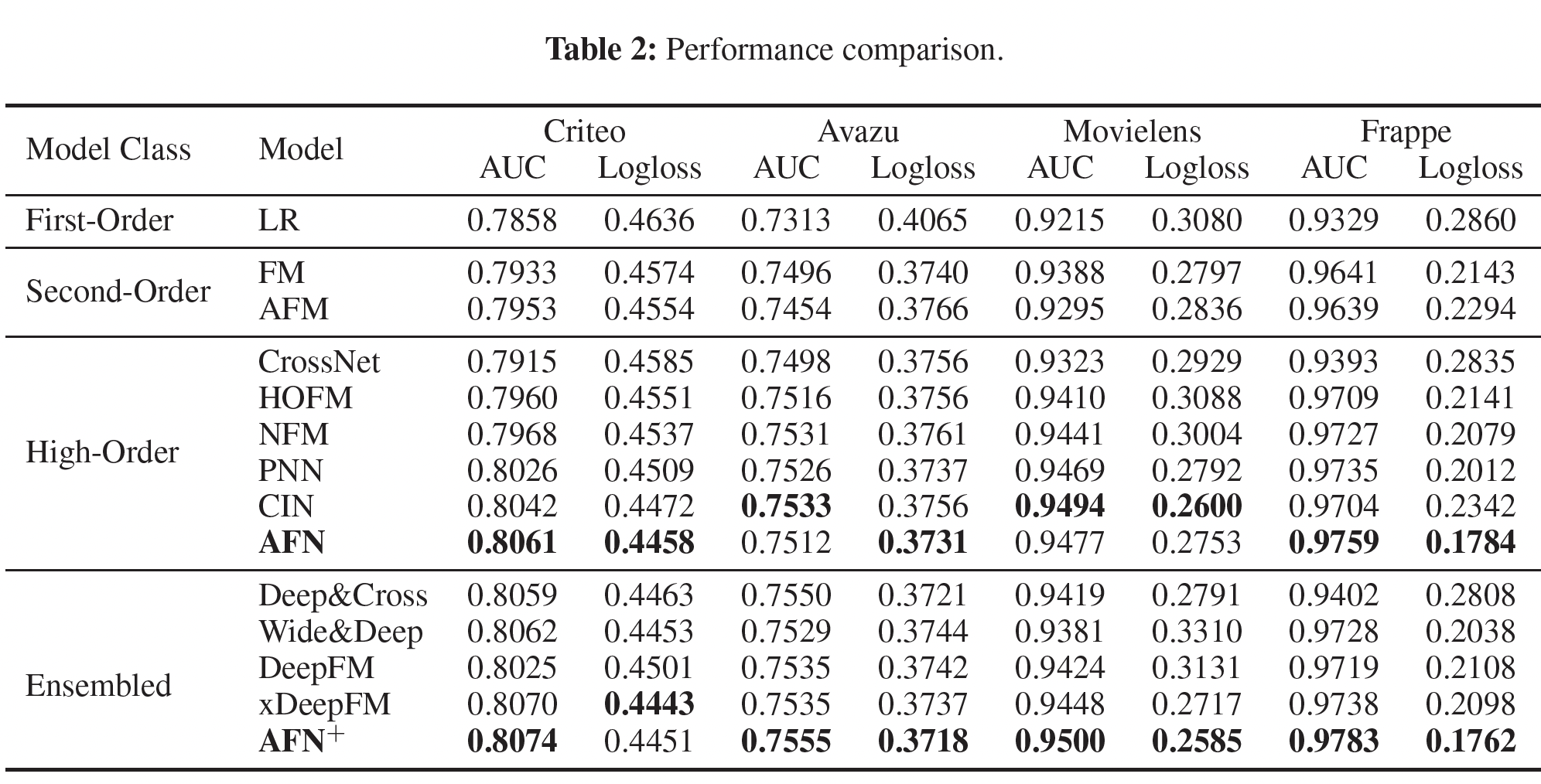
单模型的比较:单模型的比较如下表所示。可以看到:
AFN在所有的数据集上产生了最好的或有竞争力的性能。- 对于
Criteo和Frappe,AFN比第二好的模型CIN要好得多。 - 对于
Movielens,AFN取得了第二好的性能。 - 对于
Avazu,AFN取得了最好的logloss,而AUC适中。
关于较简单的模型在
Movielens和Avazu上的良好表现,我们猜测这两个数据集的预测更多依赖于低阶交叉特征,AFN的优势因此受到限制。请注意,Movielens只包含三个feature field,找到有用的高阶交叉特征的好处可能是微不足道的。- 对于
AFN在所有数据集上的表现一直优于FM和HOFM,这验证了学习自适应阶次的交叉特征比建模固定阶次的交叉特征可以带来更好的预测性能。利用高阶交叉特征的模型通常优于基于低阶交叉特征的模型,特别是当
feature field的数量很大时。这与高阶特征交互具有更强的预测能力的直觉是一致的。
AFN并没有在所有数据集上展示出显著的提升。ensemble模型的比较:ensemble模型的比较如下表所示。可以看到:AFN+在四个数据集上取得了最佳性能。平均而言,AFN相比xDeepFM,在AUC和logloss上分别取得了0.003和0.012的改善。这表明,
AFN学到的自适应阶次的交叉特征与DNN建模的隐式特征交互有很大不同,因此在结合两种不同类型的特征交互进行预测时,性能增益显著提高。
超参数研究:我们只提供
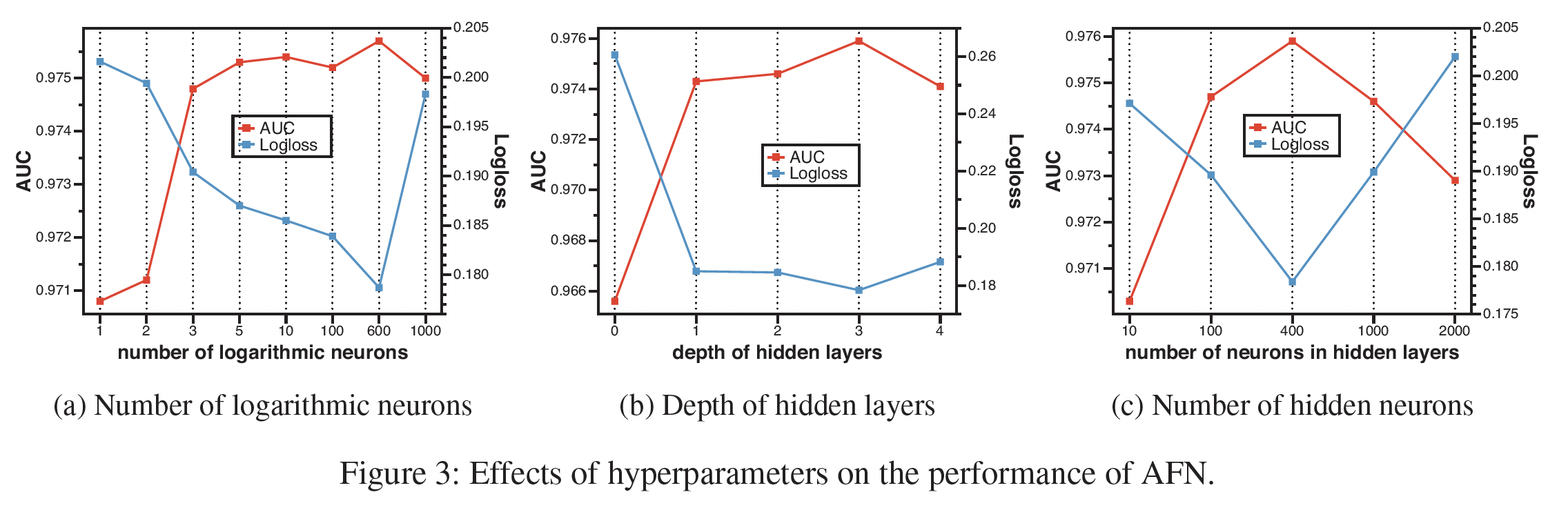
Frappe的结果,因为其他三个数据集的结果是相似的。对数神经元的数量:如下图
(a)所示:- 当神经元的数量变大时,
AFN的性能呈现上升趋势,随后是下降趋势。这表明应该采用适当数量的对数神经元,在表达能力和泛化之间做出权衡,以达到最佳性能。 - 令人惊讶的是,即使对数神经元的数量少于
5个,AFN的优势也很稳定。这一结果表明,找到少量的discriminative交叉特征对预测的准确性至关重要,而AFN对于找到这些关键的交叉特征是有效的。
- 当神经元的数量变大时,
隐层深度:如下图
(b)所示:- 在学到的自适应阶次的交叉特征上堆叠隐层有利于提高模型性能。
- 值得注意的是,
AFN的性能并不高度依赖于隐层的数量。当深度被设置为0时,AFN仍然可以取得相当好的结果。这证明了对数转换层在学习discriminative交叉特征方面的有效性。
隐层神经元数量:如下图
(c)所示:AFN的性能首先随着神经元数量的增加而增长。这是因为更多的参数给模型带来了更好的表达能力。- 当隐层的神经元数量超过
600时,性能开始下降,这是由于过拟合导致的。
学到的阶次:下图显示了在
Criteo数据集上整个训练过程中特征阶次的变化。从下图
(a)可以看到:各个feature field的阶次通常以0为中心,在[-1,1]的范围内。这与典型的factorization-based的方法截然不同,在这种方法中,每个特征的阶次要么为0、要么为1。学到的特征阶次的relaxation允许原始feature embedding在组成不同的交叉特征时被rescale。下图
(b)给出了交叉特征的阶次的分布,其中交叉特征的阶次是组成它的各个特征的阶次的绝对值之和来计算的。可以看到:在训练过程中,学到的交叉特征的阶次被逐渐优化。最终的交叉特征阶次分布在一个很宽的范围内(从
4到10),而不是像许多factorization-based方法那样被固定在一个预定义的值上(例如2)。
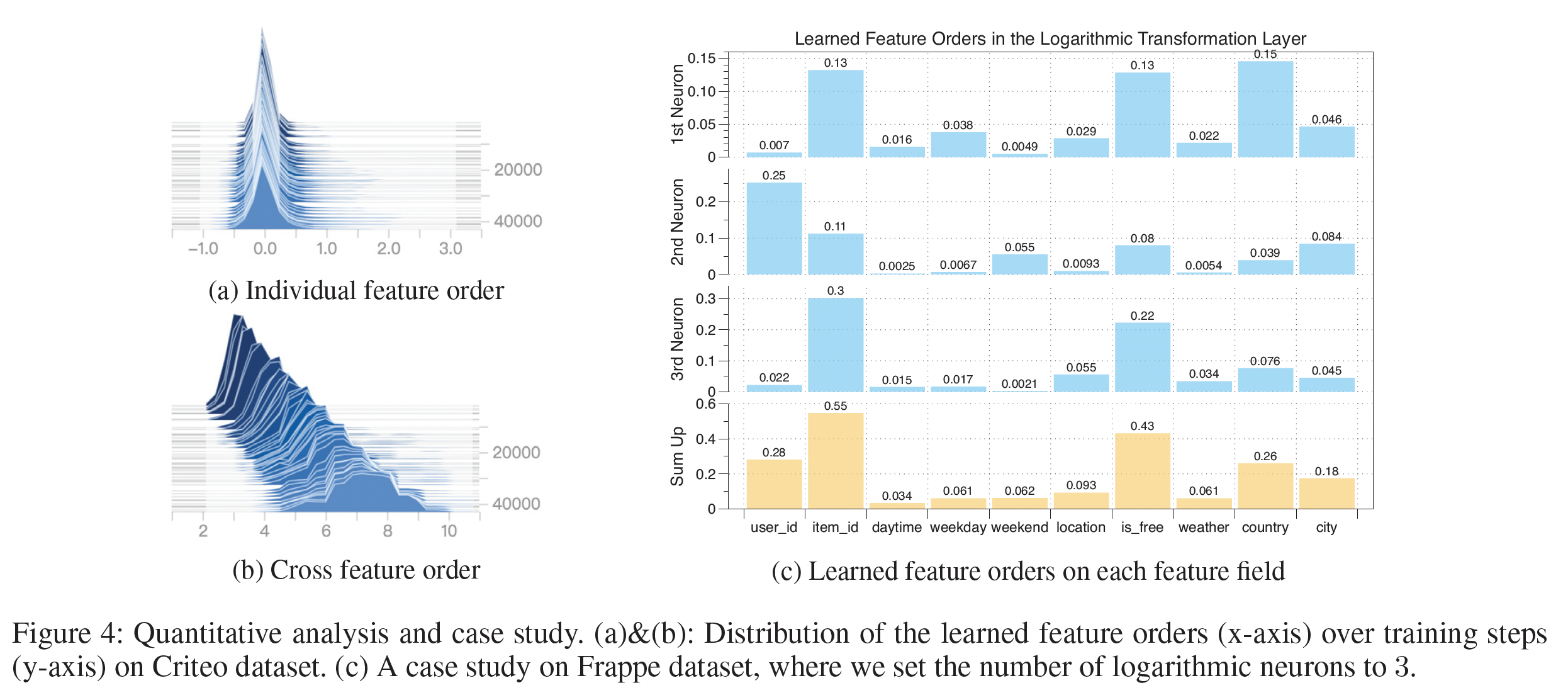
案例研究:我们对
Frappe数据集进行了案例研究。为了说明问题,我们将对数神经元的数量限制为3个。Figure 4(c)提供了每个神经元上单个特征阶次的绝对值和总和。从图中,我们可以大致推断出,三个交叉特征
(item id, is free, country), (user id, item id), (item id, is free)在各自的对数神经元中被学习。此外,通过
sum三个神经元的特征阶次,发现最discriminative的feature field是item id, is free, user id。这是合理的,因为user id和item id是协同过滤中最常用的特征;而is free表示用户是否为mobile app付费,是用户对app偏好的一个有力指标。
三十四、FGCNN[2019]
CTR预测任务的关键挑战是如何有效地建模特征交互。FM及其变体将pairwise特征交互建模为潜在向量的内积,并显示出有前景的结果。最近,一些深度学习模型被用于CTR预测,如PIN、xDeepFM等。这类模型将原始特征馈入深度神经网络,以显式或隐式的方式学习特征交互。理论上,DNN能够从原始特征中学习任意的特征交互。然而,由于与原始特征的组合空间相比,有用的特征交互通常是稀疏的,要从大量的参数中有效地学习它们是非常困难的。为解决这个困难,
Wide & Deep利用wide组件中的特征工程来帮助deep组件的学习。在人工特征的帮助下,deep组件的性能得到了显著的提高。然而,特征工程可能是昂贵的,并且需要领域知识。如果我们能通过机器学习模型自动生成复杂的特征交互,它将更加实用和鲁棒。因此,如下图所示,论文
《Feature Generation by Convolutional Neural Network for Click-Through Rate Prediction》提出了一个自动生成特征的通用框架。原始特征被馈入到机器学习模型(右图中的红框),从而识别和生成新的特征。之后,原始特征和新特征被结合起来,并馈入一个深度神经网络。被生成的特征能够通过提前捕获稀疏的但重要的特征交互来降低深度模型的学习难度。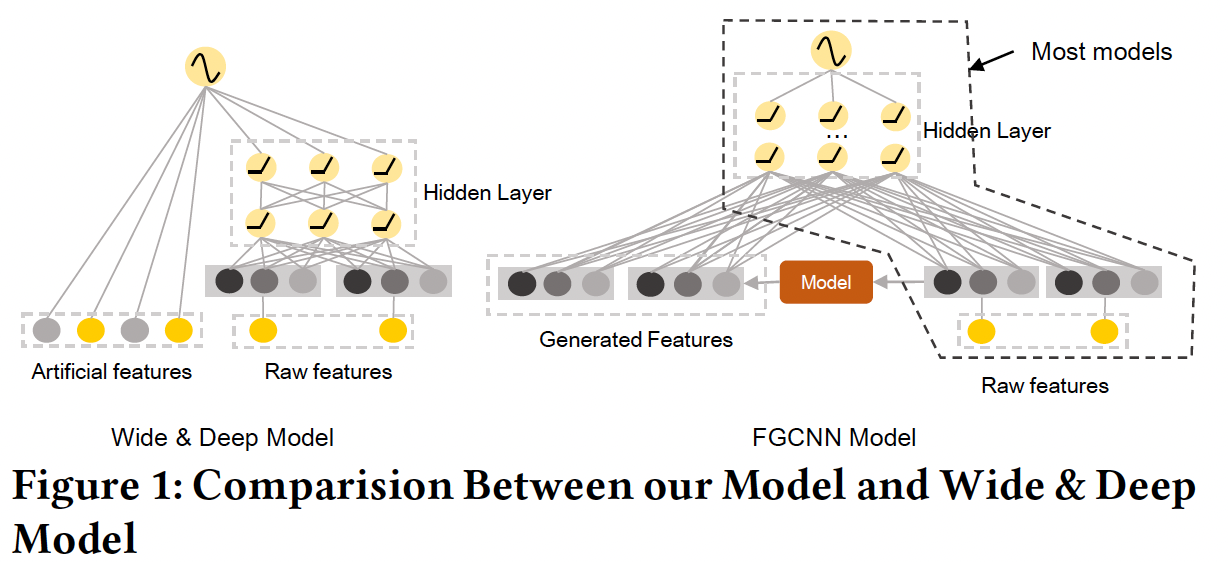
自动生成特征的最直接的方法是进行多层感知机
Multi-Layer Perceptron: MLP,并使用隐层的神经元作为生成的特征。然而,如前所述,由于有用的特征交互通常是稀疏的,MLP很难从巨大的参数空间中学习这种交互。作为一种
SOTA的神经网络结构,卷积神经网络Convolutional Neural Network: CNN在计算机视觉和自然语言处理领域取得了巨大成功。在CNN中,共享权重、池化机制的设计大大减少了寻找重要局部模式所需的参数数量,它将缓解随后的MLP结构的优化困难。因此,CNN为实现作者的想法(识别稀疏的但重要的特征交互)提供了一个潜在的良好解决方案。然而,直接应用CNN可能会导致不满意的性能。在CTR预测中,原始特征的不同排列顺序并没有不同的含义。例如,特征的排列顺序是(Name, Age, Height, Gender)还是(Age, Name, Height, Gender)对描述样本的语义没有任何区别,这与图像和句子的情况完全不同。如果只使用CNN抽取的邻居模式neighbor pattern,许多有用的global feature interaction就会丢失。这也是为什么CNN模型在CTR预测任务中表现不佳的原因。为了克服这一局限性,作者采用了CNN和MLP,两者相互补充,学习global-local特征交互来生成特征。在论文中,作者为
CTR预测任务提出了一个新的模型,即Feature Generation by Convolutional Neural Network: FGCNN,它由两个部分组成:特征生成Feature Generation、深度分类器Deep Classifier。- 在特征生成中,作者设计了一个
CNN+MLP的结构用来从原始特征中识别和生成新的重要特征。更具体地说,CNN被用来学习neighbor feature interaction,而MLP被用来重新组合它们从而提取global feature interaction。在特征生成之后,特征空间可以通过结合原始特征和新特征来进行扩充。 - 在深度分类器中,几乎所有
SOTA网络结构(如PIN、xDeepFM、DeepFM)都可以被采用。因此,论文的方法与推荐系统中SOTA的模型具有良好的兼容性。为了便于说明,作者将采用IPNN模型作为FGCNN的深度分类器,因为它在模型的复杂性和准确性之间有很好的权衡。
在三个大规模数据集上的实验结果表明,
FGCNN明显优于九个SOTA的模型,证明了FGCNN的有效性。在深度分类器中采用其他模型时,总是能取得更好的性能,这表明了所生成的特征的有用性。逐步分析表明,FGCNN中的每个组件都对最终的性能做出了贡献。与传统的CNN结构相比,论文提出的CNN+MLP结构在原始特征的顺序发生变化时表现得更好、更稳定,这证明了FGCNN的鲁棒性。综上所述,论文贡献如下:
- 确定了
CTR预测的一个重要方向:通过提前自动生成重要的特征来降低深度学习模型的优化难度,这既是必要的,也是有益的。 - 提出了一个新的模型
FGCNN用于自动生成特征和分类,它由两个部分组成:Feature Generation、Deep Classifier。特征生成利用CNN和MLP,它们相互补充,以识别重要的但稀疏的特征。 此外,几乎所有其他的CTR模型都可以应用在深度分类器中,从而根据生成的特征、以及原始的特征进行学习和预测。 - 在三个大规模数据集上的实验证明了
FGCNN模型的整体有效性。当生成的特征被用于其他模型时,总是能取得更好的性能,这表明FGCNN模型具有很强的兼容性和鲁棒性。
- 在特征生成中,作者设计了一个
相关工作:
CTR预测的浅层模型:- 由于鲁棒性和效率高,
Logistic Regression: LR模型(如FTRL)被广泛用于CTR预测中。为了学习特征交互,通常的做法是在其特征空间中手动设计pairwise特征交互。 Poly-2建模所有pairwise特征交互以避免特征工程。Factorization Machine: FM为每个特征引入了低维向量,并通过特征向量的内积来建模特征交互。在数据稀疏的情况下,FM提高了建模特征交互的能力。FFM对每个特征使用多个潜在向量,从而建模与不同field特征的交互。
LR、Poly-2、以及FM变体被广泛用于工业界的CTR预测中。- 由于鲁棒性和效率高,
CTR预测的深层模型:FNN使用FM来预训练原始特征的embedding,然后将embedding馈入全连接层。一些模型采用
DNN来改善FM,如Attentional FM、Neural FM。Wide & Deep联合训练一个wide模型和一个deep模型,其中wide模型利用人工特征工程,而deep模型学习隐式特征交互。尽管wide组件很有用,但特征工程很昂贵,而且需要专业知识。为了避免特征工程,
DeepFM引入了FM Layer(建模二阶交互)作为wide组件,并使用deep组件来学习隐式特征交互。与
DeepFM不同,IPNN(也被称为PNN)将FM Layer的结果和原始特征的embedding都馈入MLP,从而得到相当好的结果。PIN没有像DeepFM和IPNN那样使用内积来建模pairwise特征交互,而是使用一个Micro-Network来学习每个feature pair的复杂特征交互。xDeepFM提出了一种新颖的Compressed Interaction Network: CIN,以显式地建模vector-wise level的特征交互。有一些使用
CNN进行CTR预测的模型:CCPM应用多个卷积层来探索邻居特征的相关性。CCPM以一定的排列方式对neighbor field进行卷积。由于特征的顺序在CTR预测中没有实际意义,CCPM只能学习邻居特征之间有限的特征交互。《Convolutional Neural Networks based Click-Through Rate Prediction with Multiple Feature Sequences》中显示,特征的排列顺序对CNN-based模型的最终性能有很大影响。因此,作者提出生成一组合适的特征序列,为卷积层提供不同的局部信息。然而,CNN的关键弱点并没有得到解决。
在本文中,我们提出了
FGCNN模型,它将CTR预测任务分成两个阶段:特征生成和深度分类器。特征生成阶段通过生成新的特征来增强原始特征空间,而深度分类器可以采用大多数SOTA模型从而在增强的特征空间中学习和预测。与传统的CNN模型预测CTR不同,FGCNN可以利用CNN的优势来提取局部信息,并通过引入重组层来重新组合CNN学到的不同局部模式的信息来生成新的特征,从而大大缓解了CNN的弱点。在
CTR预测任务中,是否混洗特征的排列顺序,对于CNN-based模型会更好?
34.1 模型
如下图所示,
FGCNN模型由两部分组成:特征生成、深度分类器:- 特征生成侧重于识别有用的局部模式和全局模式,以生成新的特征作为原始特征的补充。
- 深度分类器则通过深度模型在增强的特征空间的基础上进行学习和预测。
除了这两个组件,我们还有
feature embedding。根据实验部分的结果,通过
CNN生成的新特征虽然有效果,但是提升不显著(平均而言不到0.1%的AUC提升)。如果将
CNN替换为MLP,那么特征生成组件就是一个MLP结构,同时将每一层的输出再投影为新的特征向量。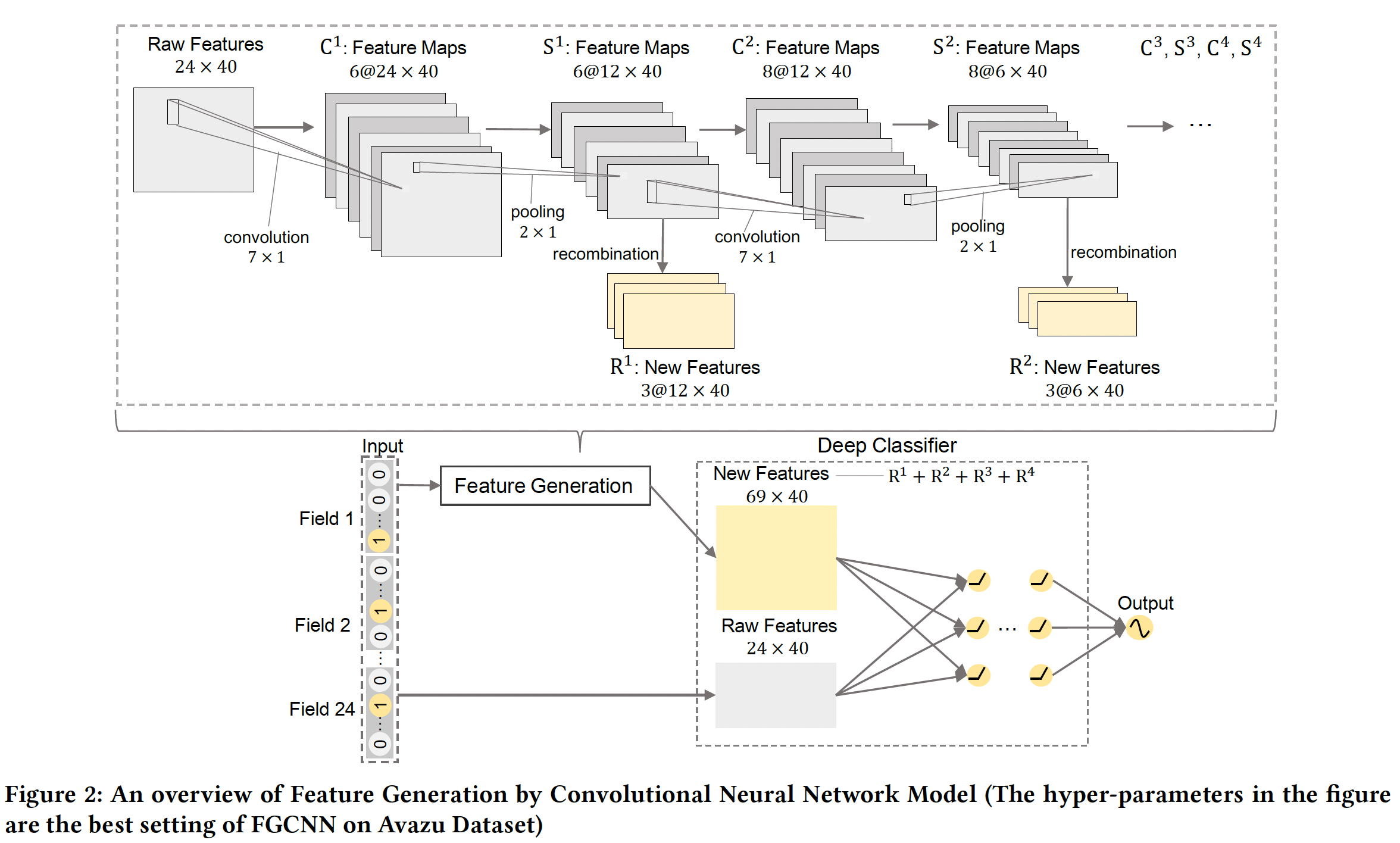
34.1.1 Feature Embedding
embedding layer应用于所有原始特征的输入,将原始特征压缩为低维向量。在我们的模型中:- 如果一个
field是univalent的(例如,Gender=Male),它的embedding就是该field的feature embedding。 - 如果一个
field是multivalent的(例如,Interest=Football, Basketball),该field的embedding是feature embeddings之和。
正式而言,在一个样本中,每个
fieldfield数量)被表示为一个低维向量embedding size。因此,每个样本可以表示为一个embedding矩阵FGCNN模型中,embedding矩阵为了避免更新参数时梯度方向的不一致,我们将为深度分类器引入另一个
embedding矩阵这意味着需要引入两套
embedding table,模型的参数要翻倍(模型参数被embedding table所主导)。如果
- 如果一个
34.1.2 Feature Generation
如前所述,从原始特征中生成新的特征有助于提高深度学习模型的性能。为了实现这一目标,特征生成组件设计了一个适当的神经网络结构来识别有用的特征交互,然后自动生成新的特征。
正如前面所论证的,由于以下原因,单独使用
MLP或CNN无法从原始特征中生成有效的特征交互:- 首先,在原始特征的组合空间中,有用的特征交互总是稀疏的。因此,
MLP很难从大量的参数中学习它们。 - 其次,虽然
CNN可以通过减少参数的数量来缓解MLP的优化困难,但它只产生neighbor feature interaction,可能会失去许多有用的global feature interaction。
为了克服单独应用
MLP或CNN的弱点,我们将CNN和MLP相互补充从而进行特征生成。下图显示了一个CNN + Recombination结构的例子,以捕捉global feature interaction。可以看到:CNN用有限的参数学习有用的neighbor feature pattern,而重组层(这是一个全连接层)根据CNN提供的neighbor pattern生成global feature interaction。因此,通过这种神经网络结构可以有效地生成重要的特征。相比直接应用MLP生成特征,这种方法的参数更少。纵向为不同的
field,横向为不同的embedding维度,卷积核为embedding维度上聚合相连的field。最后一步的结果是说明:
Recombination会把卷积结果进行投影并减少通道数。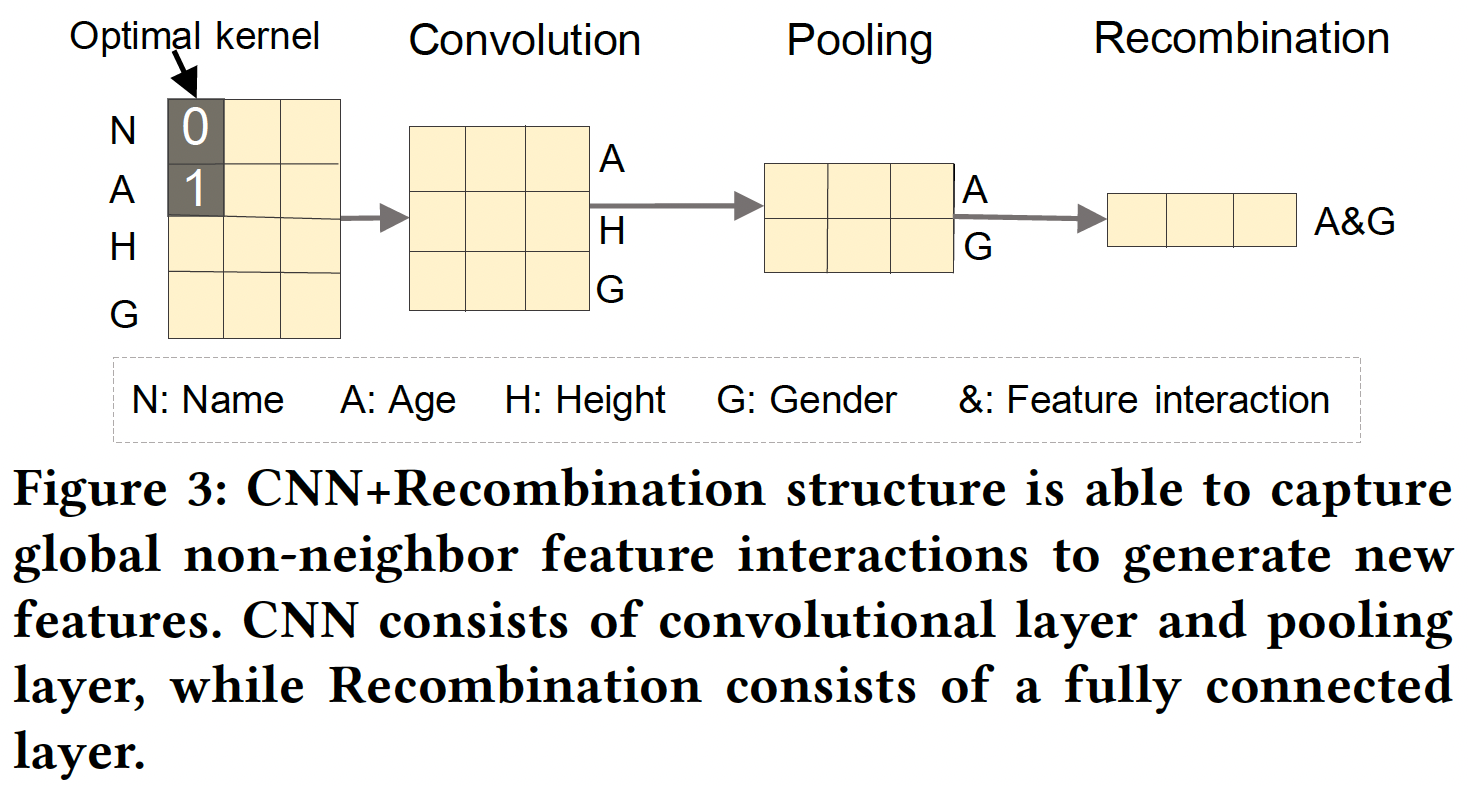
- 首先,在原始特征的组合空间中,有用的特征交互总是稀疏的。因此,
卷积层:每个样本通过
feature embedding被表示为embedding矩阵embedding矩阵reshape为1。为了捕获neighbor feature interaction,用非线性激活函数的卷积层对1,激活函数为tanh(),field进行卷积)。池化层:在第一个卷积层之后,应用一个
maxpooling层来捕获最重要的特征交互,从而减少参数的数量。令1),那么第一个池化层的输出为Recombination Layer:neighbor feature的模式。由于CNN的性质,如果neighbor feature pattern并生成重要的新特征。我们将
bias向量为其中
注意,这里是把全连接层的结果又
reshape回来。拼接:新的特征可以通过多次执行
CNN+Recombination来产生。假设有Feature Generation生成的所有的新特征为:注意,这里也有
reshape操作。原始特征和新特征的拼接为:
其中
embedding矩阵。令
embedding的数量,它等于
34.1.3 Deep Classifier
IPNN模型作为深度分类器的网络结构,因为它在模型复杂性和准确性之间有很好的权衡。事实上,任何先进的网络结构都可以被采用,这表明FGCNN与现有工作的兼容性。网络结构:
IPNN模型结合了FM和MLP的学习能力。它利用一个FM layer,通过内积运算从embedding向量中抽取pairwise特征交互。之后,input feature的embedding和FM layer的结果被拼接起来,并馈入MLP进行学习。根据IPNN原始论文的评估,IPNN的性能比PIN略差,但IPNN的效率更高。我们将对IPNN模型的网络结构进行说明。如下图所示,增强的
embedding矩阵pairwise特征交互由FM layer来建模。embedding向量个数为FM layer的输出维度为embedding向量之间两两内积。假设
FM layer的输出为MLP:其中
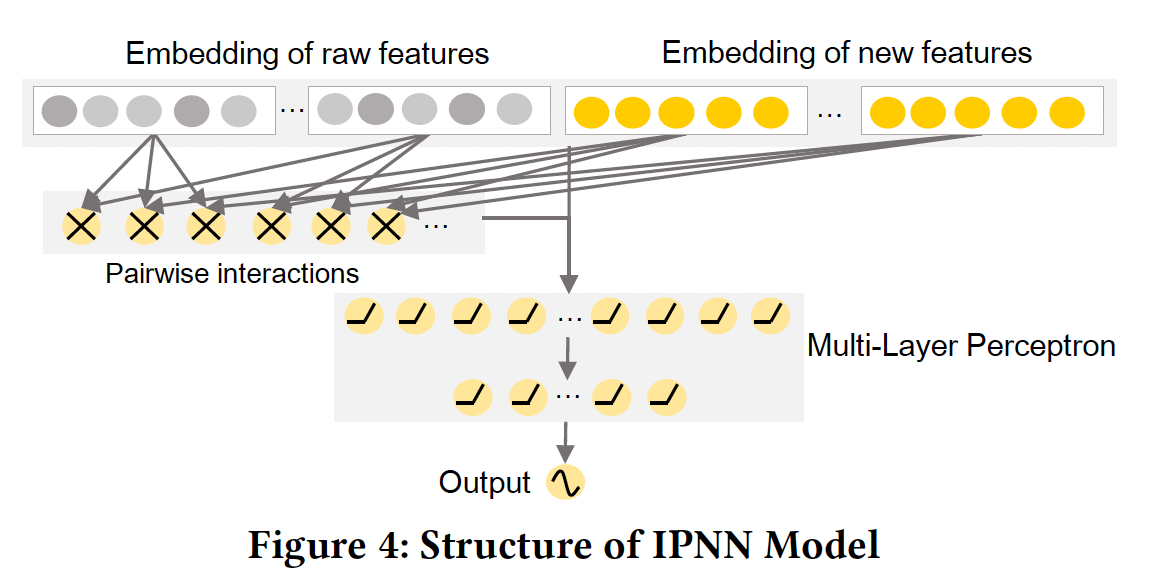
BN层:在FGCNN中,Batch Normalization应用在每个激活函数之前从而加速模型训练。目标函数:最小化交叉熵:
其中:
ground-truth,
34.1.4 复杂度分析
空间复杂度:空间复杂度由三部分组成,即
Feature Embedding、Feature Generation、Deep Classifier。Feature Embedding:包含两个embedding矩阵(一个用于feature generation、一个用于deep classifier),总的参数规模为vocab size。Feature Generation:第Deep Classifier:令Feature Generation之后所有的embedding数量(包括原始的、以及新生成的)。那么Deep Classifier的空间复杂度为:其中
MLP的隐层维度,
最终的空间复杂度大约为
embedding的数量。(具体推导见原始论文)。时间复杂度:
Feature Generation:时间复杂度约为Deep Classifier:时间复杂度约为
最终的时间复杂度约为
超参数太多了,不太好调优。
34.2 实验
数据集:
Criteo, Avazu, Huawei App Store。- 对于
Criteo数据集,我们选择"day 6-12"作为训练集,同时选择"day 13"进行评估。由于巨大的数据量和严重的类不平衡(即只有3%的样本是正样本),我们采用了负采样来保持正负比例接近1:1。我们通过分桶从而将13个numerical field离散化。field中出现少于20次的特征被设置为dummy特征"other"。 - 对于
Avazu数据集,我们以4:1的比例随机拆分为训练集和测试集。同时,我们删除了出现少于20次的特征以降低维度。 - 对于
Huawei App Store数据集,我们用20180617 ~ 20180623的日志用于训练,20180624的日志用于测试。为了减少数据量并调整正负样本的比例,采用了负采样。
数据集的统计结果如下表所示。
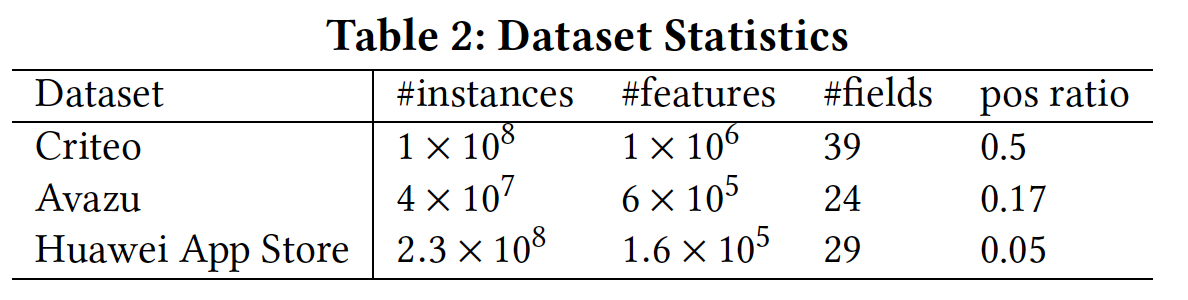
- 对于
baseline:LR, GBDT, FM, FFM, CCPM, DeepFM, xDeepFM, IPNN, PIN。Wide & Deep未参与比较,因为一些SOTA的模型(如xDeepFM、DeepFM、PIN)在各自的原始论文中显示了更好的性能。我们分别使用XGBoost和libFFM作为GBDT和libFFM的实现。在我们的实验中,其他baseline模型是用Tensorflow实现的。评估指标:
AUC, log loss。配置:下表给出了每个模型的超参数。
注意,在
Criteo和Avazu上进行实验时,我们观察到FGCNN在深度分类器中使用的参数比其他模型多。为了进行公平的比较,我们也进行了实验,增加其他深度模型的MLP中的参数。然而,所有这些模型都不能达到比原始设置更好的性能。原因可能是过拟合的问题,这类模型只是简单地使用原始特征的embedding进行训练,但使用的是复杂的结构。另一方面,由于我们的模型增强augment了特征空间并丰富了输入,因此在深度分类器中更多的参数可以提高我们模型的性能。在
FGCNN模型中,new表示对于
FGCNN和best baseline model,我们改变随机数种子并重复实验10次。我们进行wo-tailed pairwise t-test来检测FGCNN和best baseline model之间的显著差异。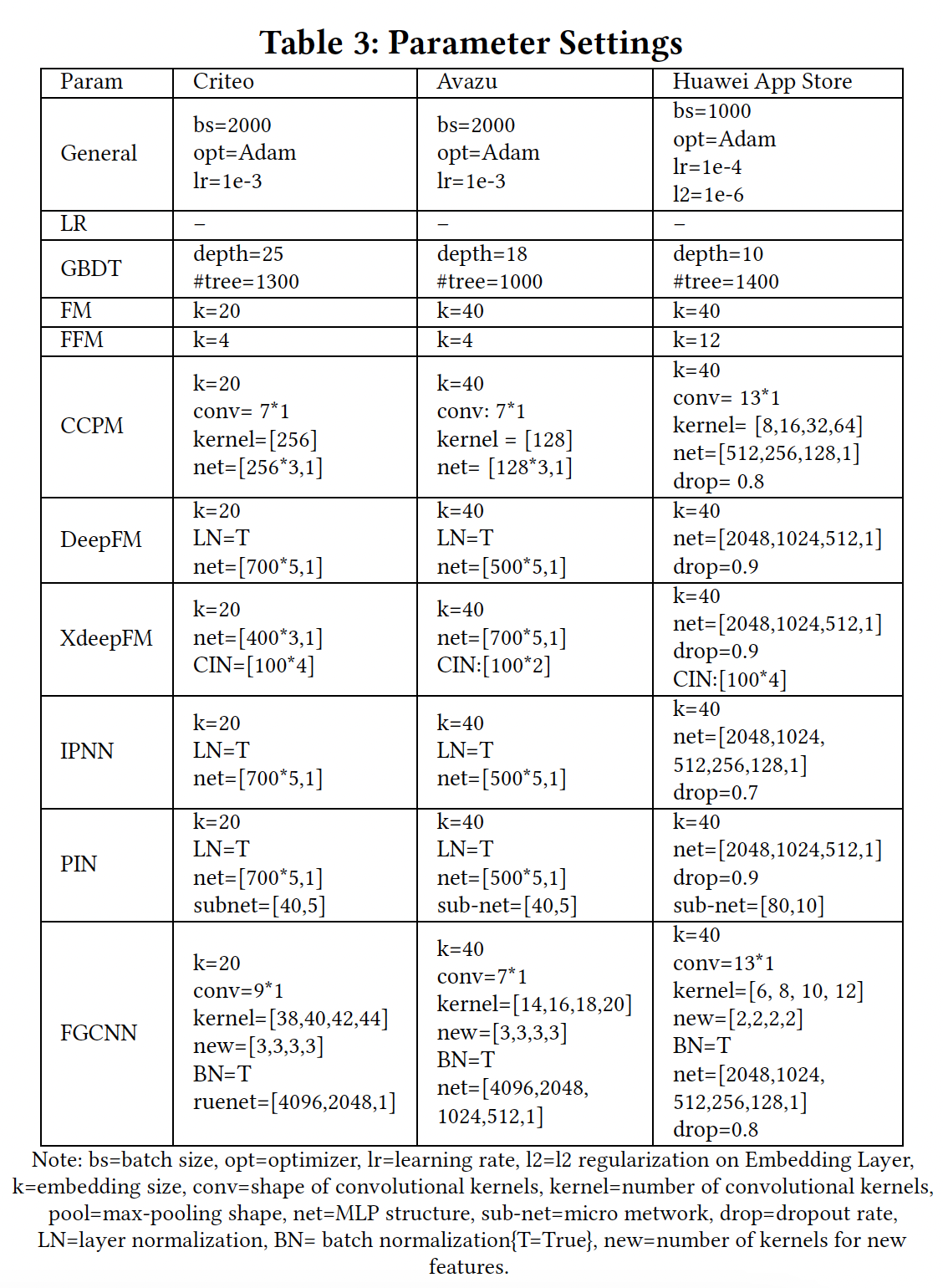
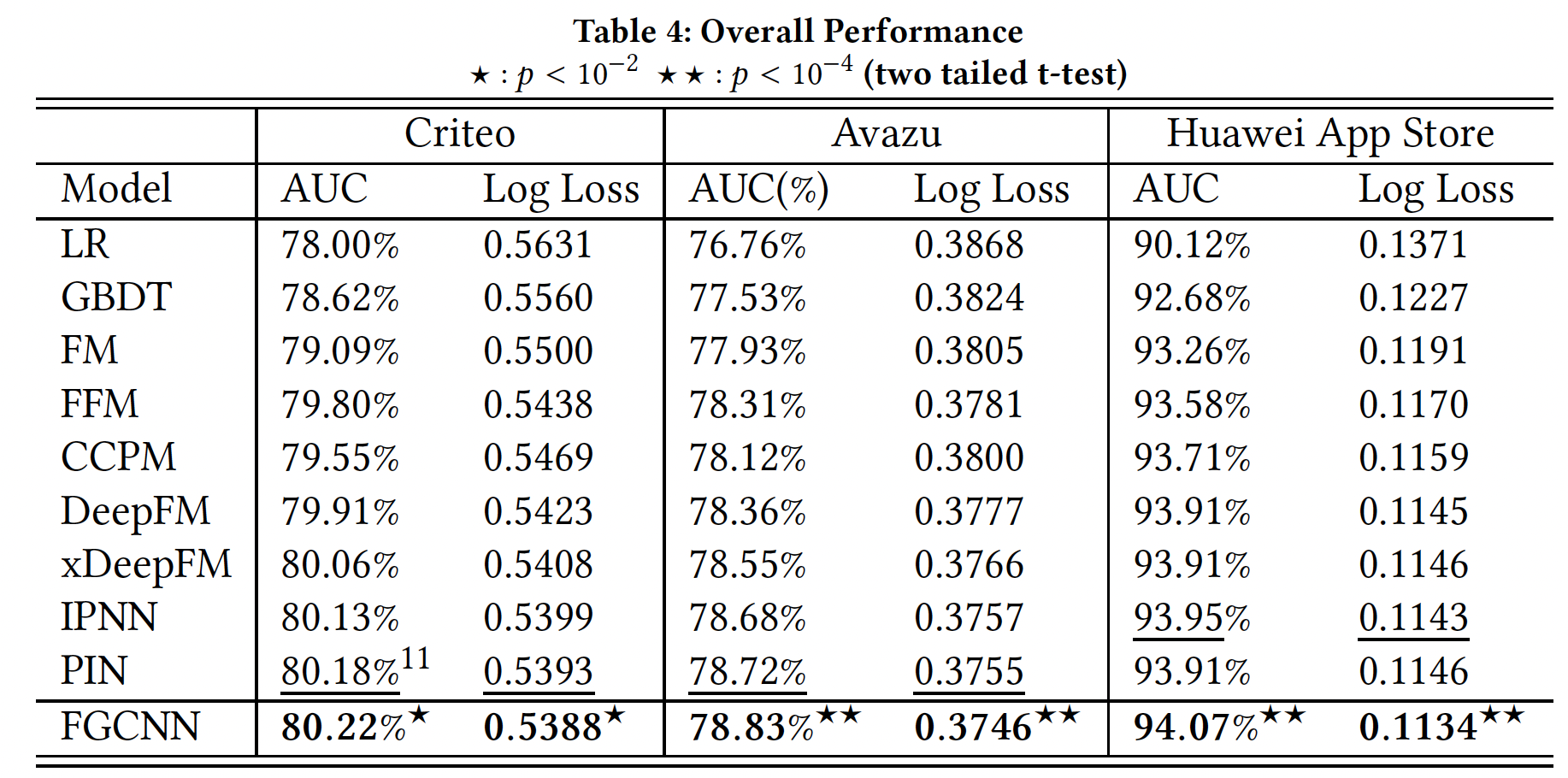
整体性能:不同模型在测试集上的表现如下,其中下划线数字是
baseline模型的最佳结果,粗体数字是所有模型的最佳结果。可以看到:首先,在大多数情况下,非神经网络模型的表现比神经网络模型差。原因是深度神经网络可以学习复杂的特征交互,比没有特征交互建模的模型(即
LR),或通过简单的内积来建模特征交互的模型(即FM和FFM)要好得多。其次,
FGCNN在三个被评估的数据集上取得了所有模型中最好的性能。它明显优于最佳baseline模型,在Criteo, Avazu, Huawei App Store数据集上的AUC分别提高了0.05%, 0.14%, 0.13%(logloss分别改善了0.09%, 0.24%, 0.79%),这表明了FGCNN的有效性。第三,在
Criteo, Avazu, Huawei App Store数据集上,在生成的新特征的帮助下FGCNN在AUC方面比IPNN分别高出0.11%, 0.19%, 0.13%(在logloss方面分别改善了0.2%, 0.29%, 0.79%)。这表明生成的特征是非常有用的,它们可以有效地减少传统DNN的优化难度,从而导致更好的性能。第四,直接应用
CNN的CCPM在神经网络模型中取得了最差的性能。此外,CCPM在Criteo数据集和Avazu数据集上的表现比FFM差。这表明,直接使用传统的CNN进行CTR预测任务是不可取的,因为CNN被设计为生成neighbor pattern,而特征的排列顺序在推荐场景中通常没有意义。然而,在
FGCNN中,我们利用CNN的优势来提取local pattern,同时辅以重组层来提取global feature interaction并生成新的特征。因此,可以实现更好的性能。
FGCNN与不同模型的兼容性:如前所述,FGCNN的深度分类器可以采用任何高级深度神经网络。这里我们选择不同的模型作为Deep Classifeir来验证特征生成的效果,结果如下表所示。可以看到:- 首先,在生成的新特征的帮助下,所有模型的性能都得到了提高,这表明了生成的特征的有效性,并显示了
FGCNN的兼容性。 - 其次,我们观察到,当只使用原始特征时,
DeepFM总是优于DNN。但是当使用被增强的特征时,FGCNN+DNN优于FGCNN+DeepFM。可能的原因是DeepFM将输入特征的内积加到了最后一个MLP层,这可能会在embeddinng上引起矛盾的梯度更新(与MLP相比)。这可能是IPNN(将乘积结果馈入MLP)在所有数据集中都优于DeepFM的原因之一。
总之,结果表明:
FGCNN模型可以被视为一个通用框架,通过自动生成新的特征来增强现有的神经网络。平均而言,
FGCNN对DeepFM和IPNN等先进模型的提升不显著。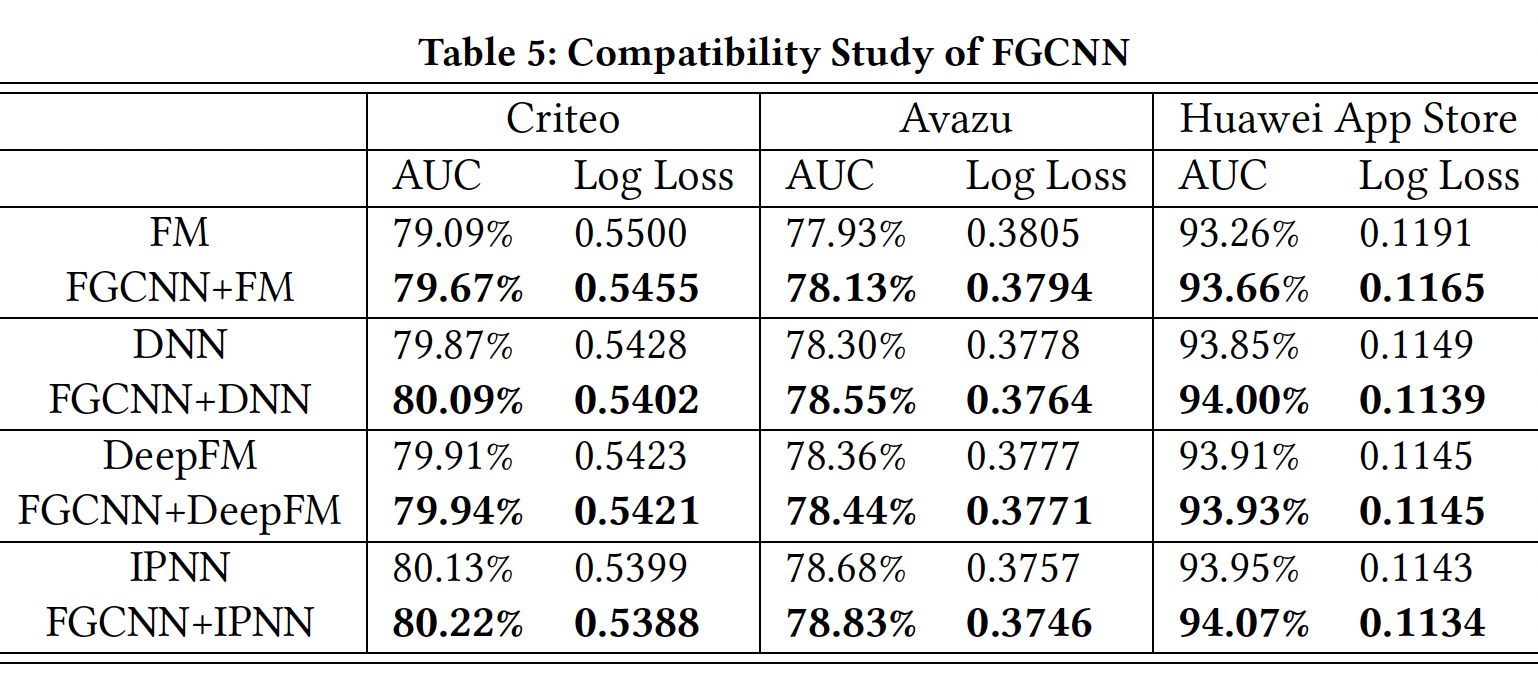
- 首先,在生成的新特征的帮助下,所有模型的性能都得到了提高,这表明了生成的特征的有效性,并显示了
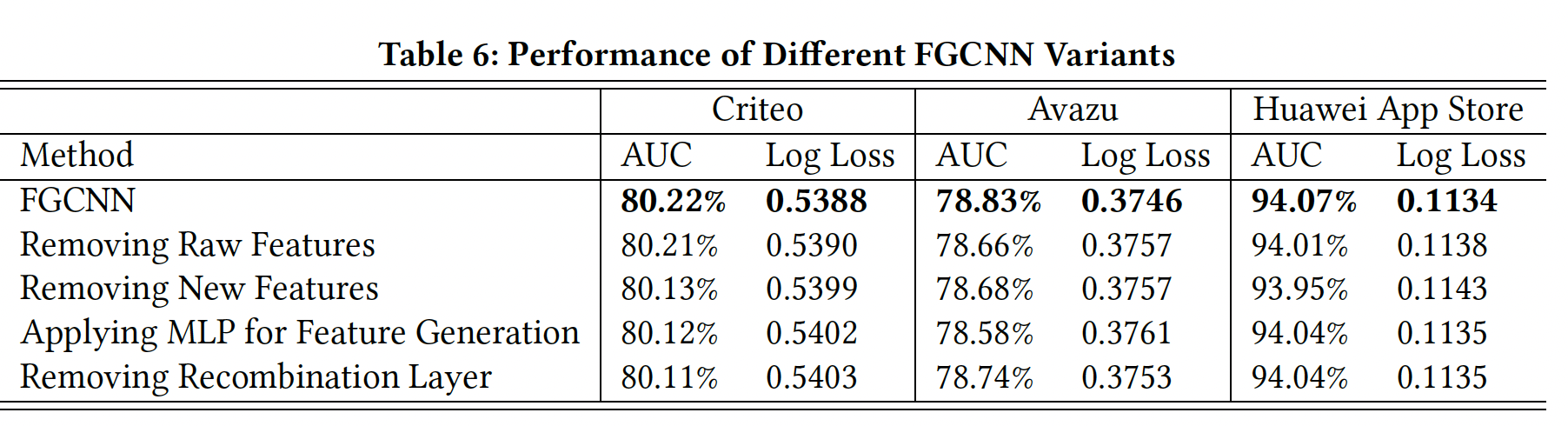
FGCNN变体的有效性:我们进行实验来研究FGCNN中的每个组件对最终性能的贡献。每个变体都是通过移除或替换FGCNN中的一些组件而产生的:Removing Raw Features:在这个变体中,原始特征没有被馈入到深度分类器中,只有生成的新特征被馈入深度分类器。Removing New Features:这个变体移除了特征生成。实际上,它等同于IPNN。Applying MLP for Feature Generation:在这个变体中,特征生成被MLP取代,MLP将每个隐层的输出作为新特征。这个变体使用相同的隐层,并在每一层生成与FGCNN相同数量的特征。Removing Recombination Layer:这个变体是为了评估重组层如何补充CNN从而捕获global feature interaction。重组层被从特征生成中移除,因此池化层的输出直接作为新特征。每层生成的新特征的数量与FGCNN保持一致。
结果如下表所示。可以看到:
首先,仅有原始特征的
FGCNN、或仅有新生成的特征的FGCNN的性能比两者兼有的FGCNN要差。这一结果表明,生成的特征是对原始特征的良好补充,这两者都很关键。移除原始特征时,效果下降不显著。此时馈入后续
Deep Classifier的输入向量长度减少一半,可以大幅降低计算量。因此,仅用新生成的特征,是一个比较好的tradeoff。其次,与
FGCNN相比,应用MLP进行特征生成的性能下降,表明MLP在从大量的参数中识别稀疏的但重要的特征组合方面效果不佳。CNN通过使用共享卷积核简化了学习的困难,它的参数少得多,可以得到所需的组合。此外,MLP重新组合由CNN提取到的neighbor feature interaction,以产生global feature interaction。第三,移除重组层将限制生成的特征为
neighbor feature interaction。由于原始特征的排列顺序在CTR预测任务中没有实际意义,这种限制会导致失去重要的nonneighbor feature interaction,从而导致性能下降。
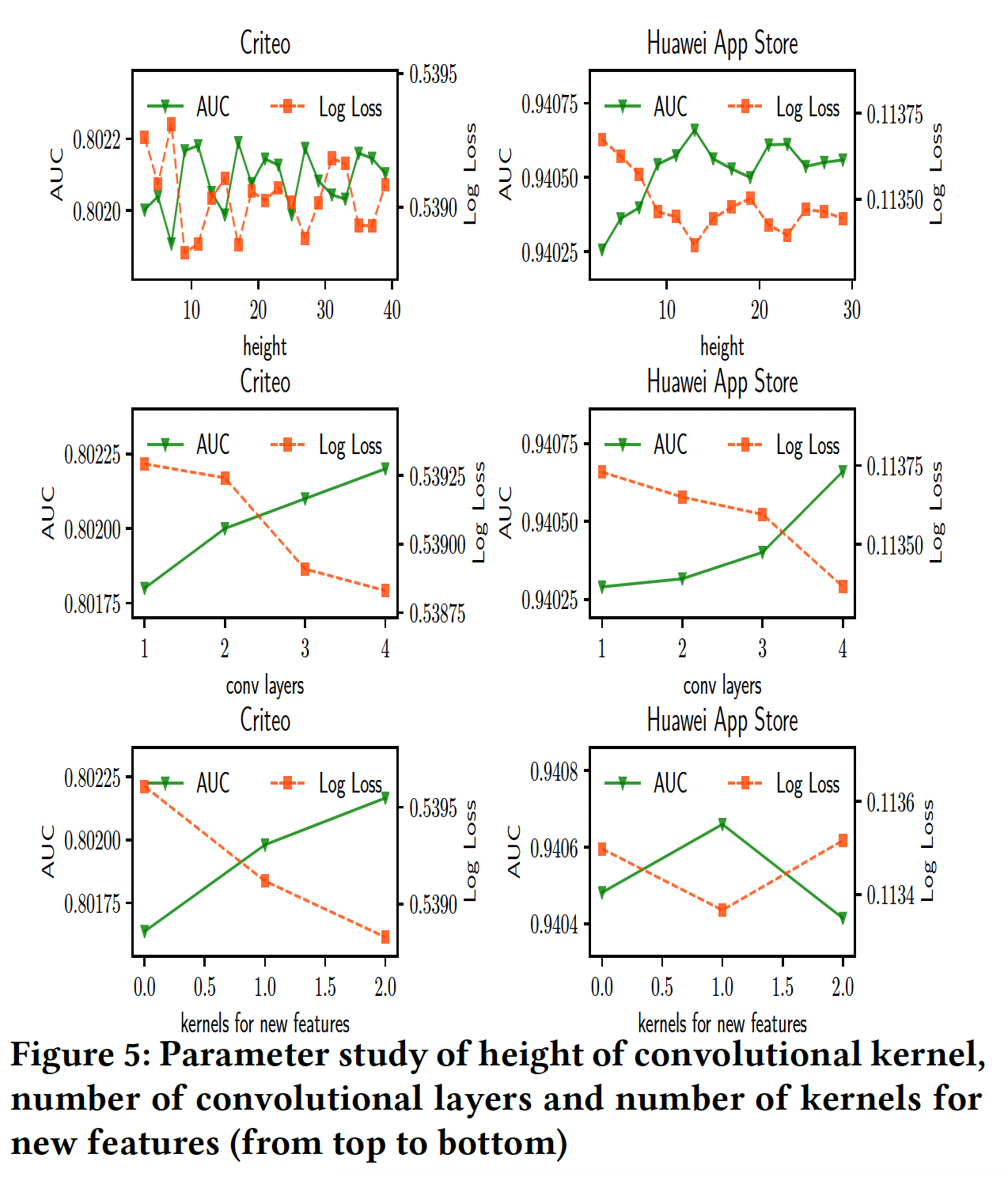
超参数研究:
FGCNN模型有几个关键的超参数,即卷积核的高度Criteo和Huawei App Store数据集上,通过改变一个超参数而固定其他参数来研究FGCNN模型的工作情况。卷积核的高度:卷积核的高度
neighbor pattern中涉及的特征就越多,但需要优化更多的参数。为了研究其影响,我们将高度从2增加到数据集的field数量可以看到:随着卷积核高度的增加,性能一般先升后降。结果表明,随着卷积核中涉及的特征越来越多,可以学习到更高阶的特征交互,从而使性能提高。然而,由于有用的特征交互通常是稀疏的,更大的高度会给有效学习它们带来更多的困难,从而导致性能下降。这一观察结果前面的发现一致,即应用
MLP进行特征生成时,性能会下降。卷积层的数量:如下图所示,随着卷积层数量
FGCNN的性能得到了提高。请注意,更多的层通常会导致更高阶的特征交互。因此,该结果也显示了高阶特征交互的有效性。用于生成新特征的核的数量:我们在不同重组层中使用相同的
这些结果验证了我们的研究思路,即:
- 首先识别稀疏的但重要的特征交互是有用的,这可以有效降低
DNN的学习难度。 - 然而,有用的特征交互可能是稀疏的和有限的。如果产生了太多的特征,额外的新特征是有噪声的,这将增加
MLP的学习难度,导致性能下降。
对原始特征的顺序进行混洗的效果:如前所述,
CNN的设计是为了捕获local neighbor feature pattern,所以它对原始特征的排列顺序很敏感。在我们的FGCNN模型中,重组层的设计是基于CNN提取的local pattern来学习global feature interaction。直观地说,如果原始特征的顺序被混洗,我们的模型应该比传统CNN的结构有更稳定的性能。因此,为了验证这一点,我们比较了两种情况的性能:with/without Recombination Layer。原始特征的排列顺序被随机地混洗多次,两个被比较的模型都是在相同的混洗后的排列顺序下进行的。如下图所示,有重组层的模型比没有重组层的模型取得了更好的、更稳定的性能。这表明,在重组层的帮助下,
FGCNN可以大大减少改变原始特征排列顺序的副作用,这也证明了我们模型的鲁棒性。根据结果来看,似乎重组层的提升也不太明显?
三十五、AutoCross[2019]
众所周知,机器学习方法的性能在很大程度上取决于特征的质量。由于原始特征很少产生令人满意的结果,因此通常进行手动
feature generation从而更好地表达数据并提高学习性能。然而,这通常是一项乏味且task-specific的工作。这促使了自动化的feature generation,这也是AutoML的一个主要话题。第四范式4Paradigm是一家致力于让更多人使用机器学习技术的公司,并且也致力于这个主题。特征交叉,即稀疏特征的叉积
cross-product,是捕获categorical feature之间的交互的一种很有前途的方法,广泛用于增强从表格数据中的学习。表格数据中,每一行对应一个样本、每一列对应一个distinct特征。- 特征交叉表示特征的共现,它可能与
target label高度相关。例如,交叉特征"job x company"表示一个人在特定公司从事特定工作,这是预测个人收入的一个强大特征。 - 特征交叉还增加了数据的非线性,这可能会提高学习方法的性能。例如,线性模型的表达能力受到其线性的限制,但可以通过交叉特征来扩展。
- 最后但并非最不重要的是,显式生成的交叉特征具有高度的可解释性,这是许多真实世界业务中的一个吸引人的特性,例如医疗和欺诈检测。
然而,枚举所有交叉特征可能会导致学习性能下降,因为它们可能是不相关的或冗余的,会引入噪声,并增加学习难度。因此,只应生成有用且重要的交叉特征,但它们通常是
task-specific。在传统的机器学习应用中,人类专家大量参与特征工程,努力为每项任务生成有用的交叉特征,并以试错的方式使用其领域知识。此外,即使是经验丰富的专家,当原始特征的数量很大时也可能会遇到麻烦。人工特征交叉的人力需求和难度大大增加了应用机器学习技术的总成本,甚至阻碍了许多公司和组织充分利用其数据。这提出了对自动特征交叉的巨大需求,这是论文
《AutoCross: Automatic Feature Crossing for Tabular Data in Real-World Applications》提出的工作目标。除了主要目标,即以高效率的、高效果的方式自动化特征交叉之外,论文还需要考虑其他几个要求:简单性要求:用户友好且易于使用。
大多数现有的自动特征生成方法的性能在很大程度上取决于一些超参数。如
ExploreKit中的阈值、《Simple and scalable response prediction for display advertising》中的降采样率、以及基于深度学习的方法中的网络架构。这些超参数应该由用户为每个specific task正确确定或仔细调优,这需要用户有专业的机器学习知识。分布式计算:现实世界企业中的大量的数据和特征使得分布式计算成为必须。特征交叉方法应考虑计算成本、传输成本、以及存储成本。
实时推理需求:实时推理涉及许多真实世界的业务。在这种情况下,一旦输入了实例,就应该立即生成特征并进行预测。
总结上述需求,自动特征交叉工具需要具有高效果、高效率、简单性,能够针对分布式计算进行优化,并实现快速推理。为了解决这些挑战,论文提出了
AutoCross。AutoCross是一种自动特征交叉工具,专门为具有大量categorical feature的表格数据设计。论文主要贡献如下:
- 提出了一种高效的
AutoML算法,从而在广泛的搜索空间中显式地搜索有用的交叉特征。它能够构造高阶交叉特征,这可以进一步提高学习性能。 AutoCross具有高度简单性和最小化的超参数暴露。论文提出successive mini-batch gradient descent和多粒度离散化。它们提高了特征交叉的效率和效果,同时避免了仔细的超参数设置。AutoCross针对分布式计算进行了充分优化。通过设计,这些算法可以降低计算成本、传输成本、和存储成本。- 在
benchmark和真实世界数据集上进行大量实验,结果验证了AutoCross的效率和效果。它可以显著提高广义线性模型的性能,同时保持较低的推理延迟。研究还表明,AutoCross可以结合深度模型,这意味着可以结合显式特征生成和隐式特征生成的优势,进一步提高学习性能。
- 特征交叉表示特征的共现,它可能与
相关工作:这里简要回顾与
AutoCross大致相关的一些工作,并说明它们不符合我们的目的的原因。FM寻求原始特征的低维embedding,并捕获它们的交互。然而,这种交互并不是显式地被构建的(通过embedding被间接地构建)。此外,FM可能过度泛化和/或引入噪声,因为FM枚举了所有可能的交互,而不管该交互是否有用。- 还有一些
embedded feature selection/generation方法,如group lasso和gradient boost machine: GBM,它们本质上伴随着模型训练来识别、或隐式地构建有用的特征。然而,这些方法通常难以处理large scale问题(其中,从categorical feature生成了高维稀疏数据),和/或计算问题(当特征数量很大时,如考虑高阶特征交叉)。 - 最后,
itemstes在数据挖掘社区中得到了很好的研究。与交叉特征一样,它们也表示属性的共现。然而,不同之处在于itemsets中的元素通常是相同的类型,例如,所有元素都是商品。此外,itemsets主要用于rule-based的机器学习技术,如frequent pattern和association rule。这些技术可能难以推广,并且在规则数量较大时推理速度较慢(因为检索成本高)。
35.1 模型
35.1.1 动机
通过对原始特征的叉积的结果进行向量化来构建交叉特征:
其中:
one-hot encoding或哈希技巧);vec()函数把张量展平为向量;交叉特征也是二元的特征向量。如果交叉特征使用三个或更多个原始特征,我们称它为高阶交叉特征。这里将陈述我们工作的动机。
虽然大多数早期的自动特征生成工作集中于原始特征的二阶交互,但是趋势表明:考虑更高阶(即,阶次高于两阶)的交互将使得数据更
informative和discriminative。与其他高阶交互一样,高阶交叉特征可以进一步提高数据质量,提高学习算法的预测能力。例如三阶交叉特征item x item x region可以是在某些节日期间推荐区域性偏好的食物的一个强大特征。然而,在现有的工作中还没有发现高阶交叉特征的显式生成。接下来,我们将说明:现有的特征生成方法要么不能生成高阶交叉特征、要么不能满足我们的业务需求。一方面,基于搜索的
feature generation方法采用显式搜索策略来构造有用的特征或特征集。许多这样的方法专注于数值特征,并且不生成交叉特征。至于现有的特征交叉方法,它们没有设计成执行高阶特征交叉。另一方面,存在基于深度学习的
feature generation成方法,其中特征之间的交互由特定网络隐式地或显式地表达。人们提出了各种深度学习模型来处理categorical特征,如FM、PNN等。还有一些工作将深度学习模型和额外的结构相结合,这些结构包括:- 手动设计的特征,如
Wide & Deep。 FM,如DeepFM, xDeepFM。- 其它特征构建组件,如
Deep & Cross Network。
其中,
xDeepFM提出了一种compressed interaction network: CIN来显式捕获embedded feature之间的高阶交互,并证明优于上述其它基于深度学习的方法。这是通过对embedded feature之间执行element-wise乘积来实现的:其中:
embedding矩阵,emebdding size。然而,如以下
Proposition所述,上述方法得到的特征仅仅是embedded high-order cross feature的特殊情况。此外,深度模型在推理方面相对较慢,这使得我们必须在实时推理系统中部署模型压缩或其他加速技术。- 手动设计的特征,如
Proposition:存在无限多具有embedding矩阵embedding矩阵证明见原始论文的附录。
受高阶交叉特征的有用性、以及现有工作的局限性的启发,在本文中,我们旨在提出一种新的自动特征交叉方法,该方法足够有效地、高效地自动生成高阶交叉特性,同时满足我们的业务需求(即简单、针对分布式计算进行优化,并实现快速推理)。下表比较了
AutoCross和其他现有方法。
35.1.2 AutoCross
下图给出了
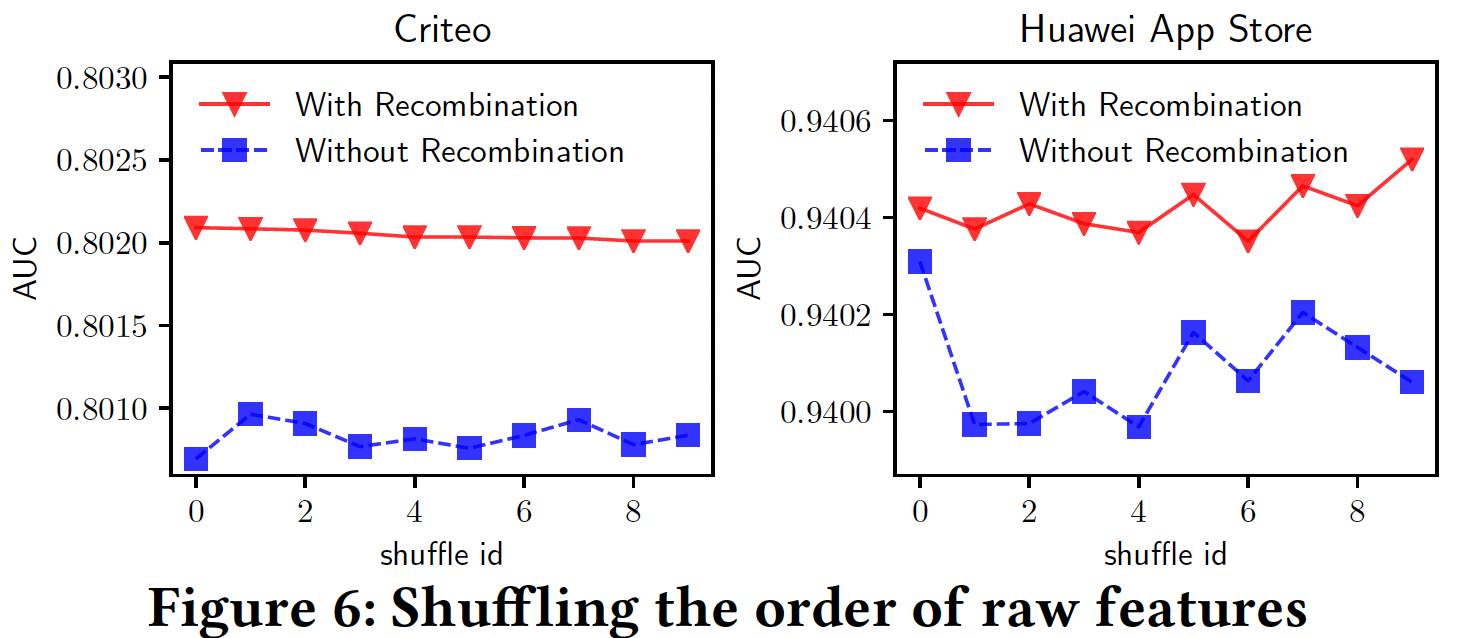
AutoCross的概览,其中包括三个部分:通用工作流、组件算法、底层基础设施。从用户的角度来看,
AutoCross是一个黑匣子,它将训练数据和特征类型(即categorical、numerical、时间序列等等)作为输入,并输出一个feature producer。feature producer可以快速执行AutoCross学到的crossing从而转换输入数据,然后用于模型训练或推理。feature producer使用哈希技巧来加速特征生成。与基于深度学习的方法相比,feature producer占用的计算资源明显更少,因此特别适合于实时推理。在黑匣子(下图中的
"Flow"部分)内,数据将首先进行预处理,其中包括确定超参数、填充缺失值、数值特征离散化。然后,在由两个步骤组成的循环中迭代构建有用的特征集:- 特征集生成:生成具有新的交叉特征的候选特征集。
- 特征集评估:评估候选特征集并选择最佳的作为新的解决方案。
一旦满足某些条件,该迭代过程就终止。
从实现的角度来看(下图中的
"Infrastructures"部分),AutoCross的基础是基于参数服务器(parameter server: PS)架构的分布式计算环境。数据按block缓存在内存中,每个block包含一小部分训练数据(这里指的是所有样本的一小部分特征,而不是一小部分样本的所有特征)。worker访问缓存的data block,生成相应的特征,并对其进行评估。特征管理器控制特征集的生成和评估。过程管理器控制特征交叉的整个过程,包括超参数适配、数据预处理、工作流控制、以及程序终止。连接工作流程和基础设施的算法是本文的主要重点(下图的
"Algorithms"部分)。每种算法都对应于工作流程中的一部分:- 我们使用
beam search来生成特征集,以探索广泛的搜索空间。 - 我们使用
field-wise逻辑回归和successive mini-batch gradient descent来评估特征集。 - 我们使用多粒度离散化来进行数据预处理。
这些算法的选择、设计和优化考虑了分布式计算的简单性和成本。
AutoCross算法的原理比较简单明了,但是需要基础架构的支持,不太容易在实践中使用。此外,
AutoCross仅能评估表格型数据,无法处理序列特征、也无法处理multi-set特征(即,一个field上取多个值),更无法处理图片和文本特征。- 我们使用
问题定义:为了便于讨论,首先我们假设所有原始特征都是
categorical的。数据以multi-field categorical的形式表示,其中每个field是通过encoding(one-hot encoding或哈希技巧)从categorical feature中生成的binary向量。给定训练数据现在,我们定义
feature crossing problem为:其中:
特征集生成:假设原始特征集的大小为
所有可能的特征集合为
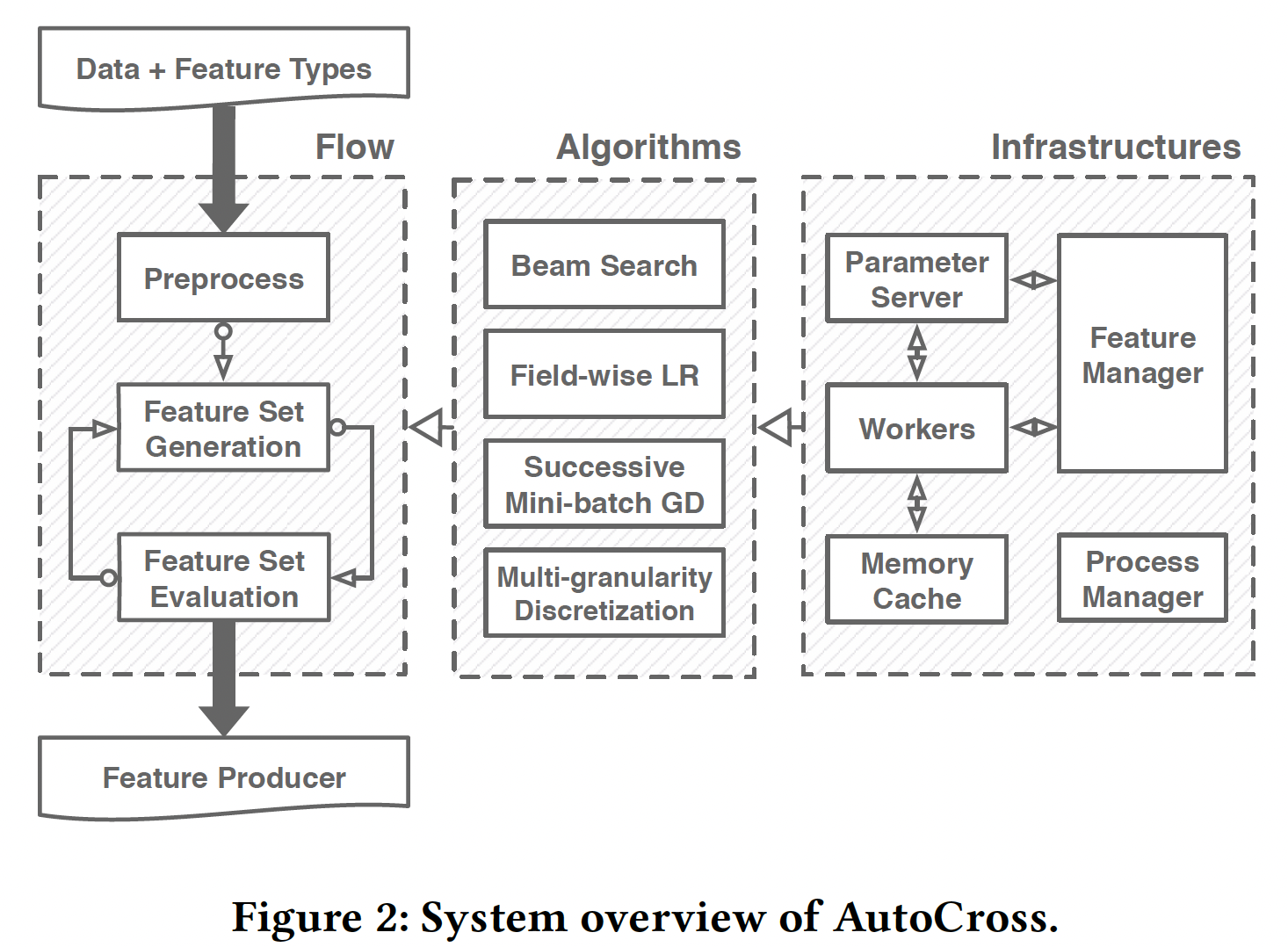
在
AutoCross中,我们考虑下图所示的树结构空间A和B的交叉表示为AB,更高阶的交叉特征也是类似的表示方式。对于一个节点(一个特征集),它的每个子节点都是通过在当前节点的基础上添加自身元素的一个pair-wise crossing来构造的。交叉特征之间(或交叉特征和原始特征之间、原始特征和原始特征之间)的pair-wise交互将导致高阶特征交叉。树结构空间
beam search来进一步提高效率。beam search的基本思想是在搜索过程中只扩展最有前途的节点:- 首先,我们生成根节点的所有子节点,评估它们对应的特征集,然后选择性能最佳的子节点进行下一次访问。
- 在接下来的过程中,我们扩展当前节点并访问其最有希望的子节点。
当过程终止时,处于结束位置的节点就是我们得到的结果特征集。
通过这种方式,我们在大小为
{A, B, C, D}开始,到解决方案{A, B, C, D, AB, CD, ABC, ABCD}结束。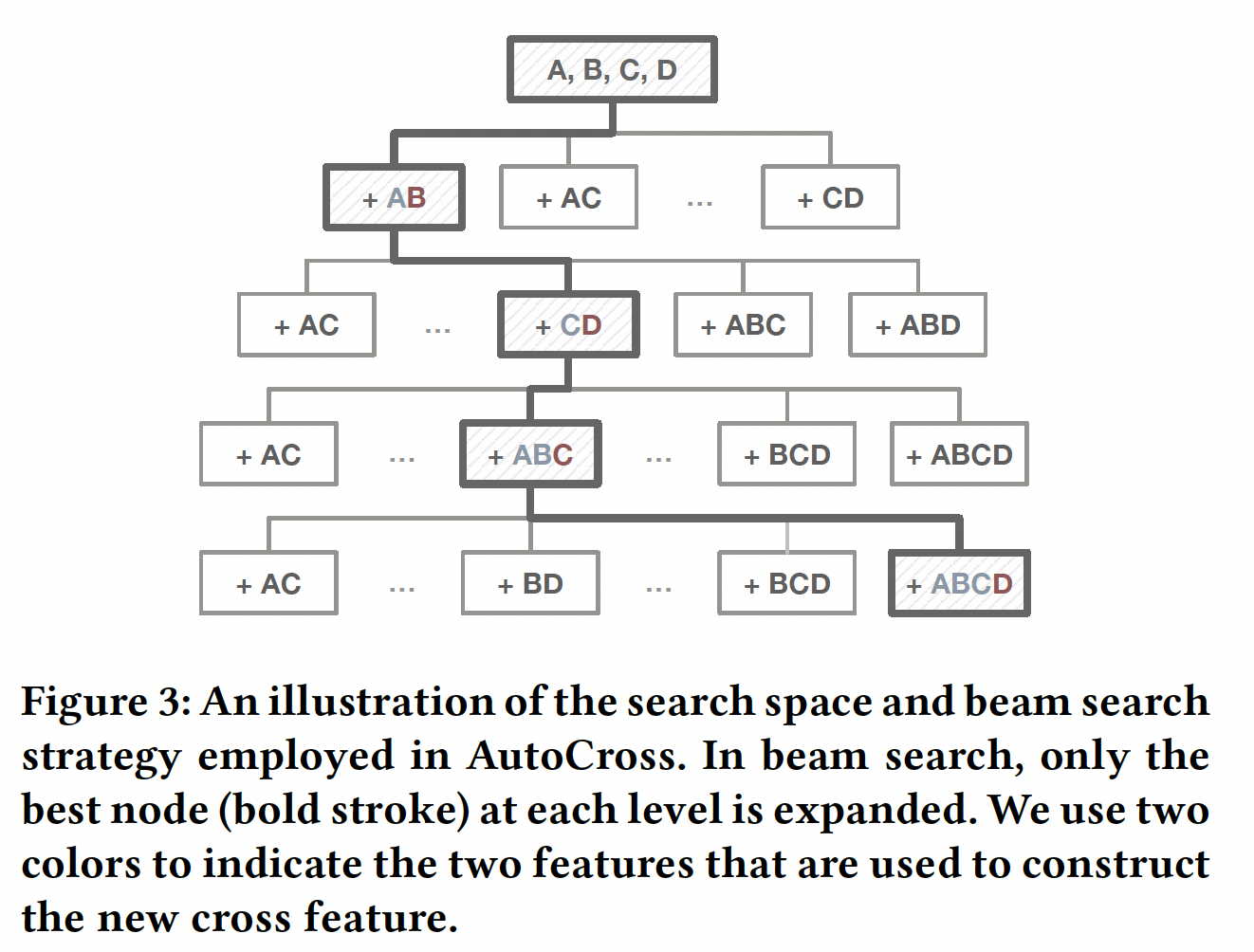
AutoCross中特征集选择算法:输入:原始特征集
输出:结果特征集
算法步骤:
初始化当前节点:
迭代直到满足停止条件:
- 特征集生成:通过将
pair-wise crossing添加到crossing)。 - 特征集评估:对所有这些子节点进行评估,得到最佳子节点
- 替换:
- 特征集生成:通过将
这里的
beam size = 1,也可以考虑beam size = s,特征集评估:特征集选择算法的关键步骤是评估候选特征集的性能。这里候选集
AutoCross中提出了field-wise逻辑回归和successive mini-batch。field-wise逻辑回归:我们加速特征集评估的第一个努力是field-wise逻辑回归(field-wise LR)。这里进行了两种近似:首先,我们使用用
mini-batch梯度下降训练的逻辑回归来评估候选特征集,并使用相应的性能来近似实际使用的学习算法其次,在模型训练期间,我们只学习新添加的交叉特征的权重,而其他权重是固定的。因此,训练是
'field-wise'的。例如,假设当前的特征集是AB特征的权重需要被学习。具体而言,给定一个样本,假设
LR模型为:其中:
下图展示了
field-wise LR如何在参数服务器架构上工作。field-wise LR从几个方面提高了特征集评估的效率:- 存储:
worker只存储sparse格式)和representation。在内存缓存中存储 - 传输:内存缓存和
worker之间的传输内容是representation。 - 计算:只更新
worker和parameter server的计算负担。所有worker都直接获取存储的worker的每个mini-batch重复计算
一旦
field-wise LR完成,我们就在验证集AUC, accuracy, negative logloss等指标来评估field-wise LR的有效性。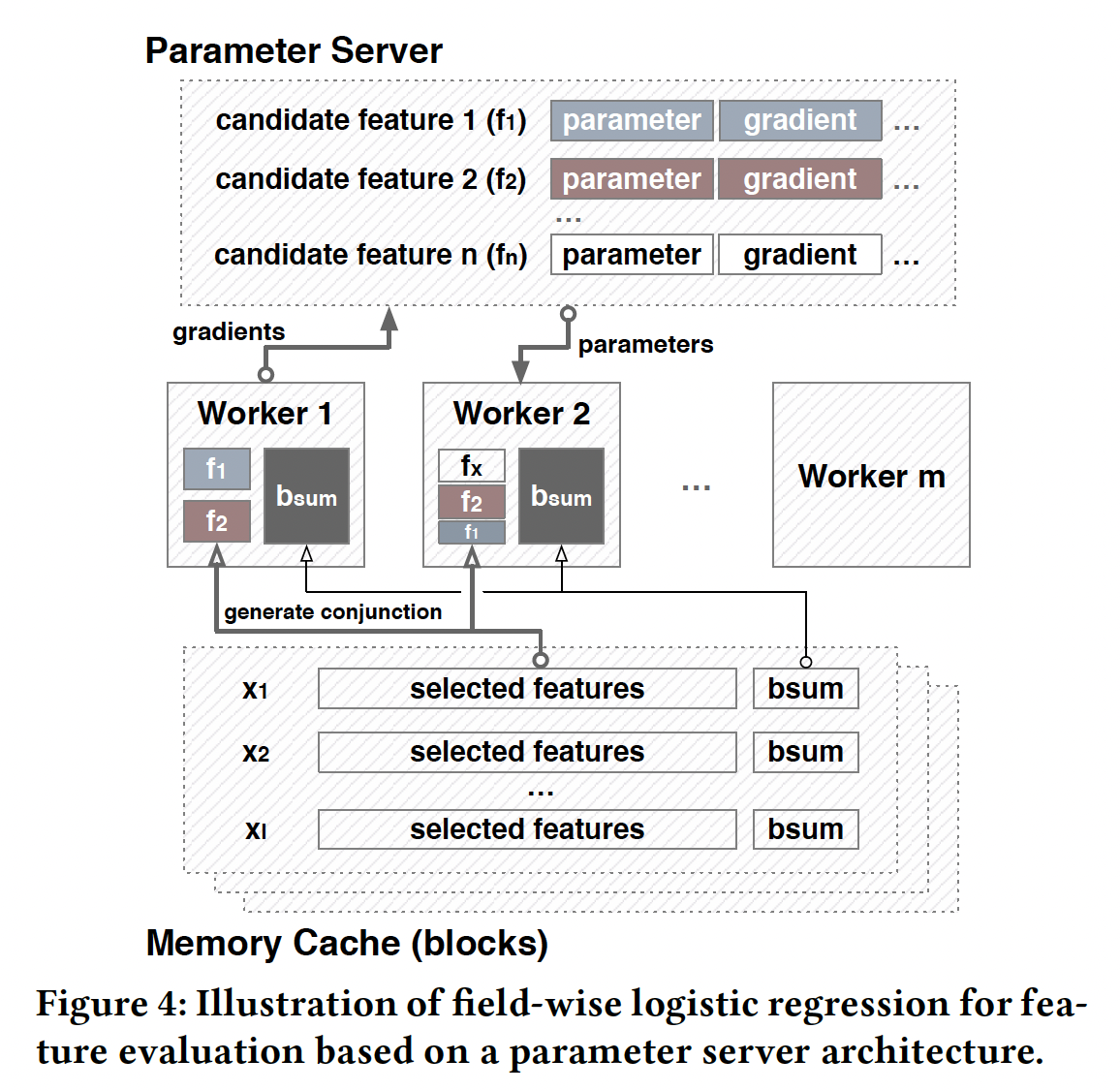
Successive Mini-batch Gradient Descent:在AutoCross中,我们使用successive mini-batch gradient descent方法来进一步加速field-wise LR的训练。这是由最初针对multi-arm bandit问题提出的successive halving算法所推动的。successive halving的特点是计算资源的高效分配和高度简单。在我们的例子中,我们将每个候选特征集视为一个
arm,拉动手臂就是用数据块训练相应的field-wise LR模型。拉动手臂的即时回报是partially trained model的验证AUC。训练数据平均分为successive mini-batch gradient descent将更多的资源分配给更有前景的候选集。唯一的超参数mini-batch size和采样率。可以看到:
- 在训练的早期,数据块的数量较少,此时更多的候选特征集会被评估。
- 在训练的后期,数据块的数量较多,此时只有最优秀的候选特征集会被评估。
每次迭代之后,数据块翻倍、候选特征集的数量减半。
Successive Mini-batch Gradient Descent: SMBGD算法:输入:所有的候选集
输出:最佳候选集
算法步骤:
迭代:
- 使用
field-wise LR模型。 - 在验证数据集上评估所有候选集
- 保留头部
50%的候选集: - 如果
- 使用
预处理:在
AutoCross中,我们在数据预处理步骤中对数值特征进行离散化。为了实现离散化的自动化并避免对人类专家的依赖,我们提出了一种多粒度离散化方法。基本思想很简单:我们将每个数值特征离散化为几个categorical feature而不是一个categorical feature,每个categorical feature具有不同的粒度,而不是微调粒度。下图给出了用四个级别的粒度来离散化数值特征的示例。由于考虑了更多级别的粒度,因此更可能获得有前景的结果。为了避免离散化导致的特征数量急剧增加,一旦生成了这些特征,我们就使用
field-wise LR(不考虑剩下的问题是如何确定粒度级别。经验丰富的用户可以人工设置一组值。如果未指定任何值,
AutoCross将使用此外,
AutoCross将在预处理步骤中调用超参数调优程序,以找到LR模型的最佳超参数。它们将在随后涉及的所有LR模型中使用。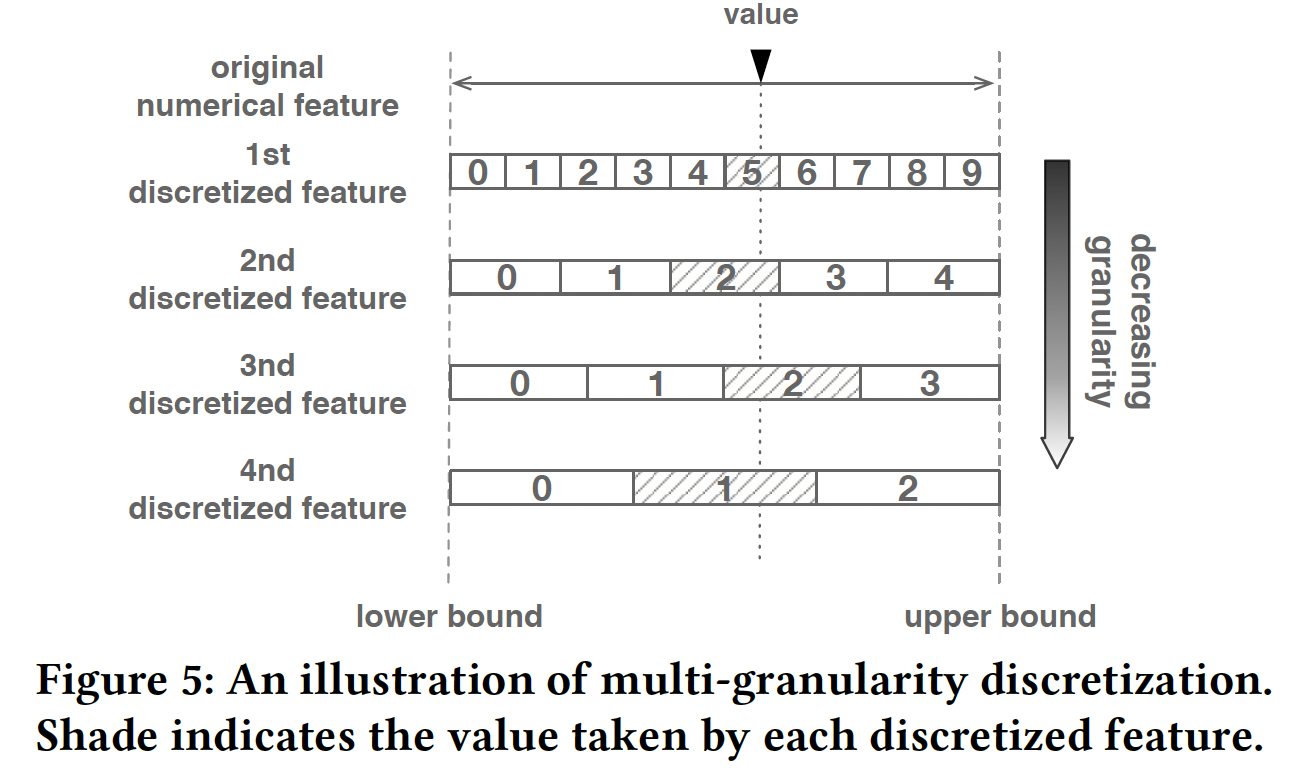
Termination:AutoCross使用三种终止条件:- 运行时条件:用户可以设置
AutoCross的最大runtime。时间过去后,AutoCross终止并输出当前解决方案 - 性能条件:在生成新的特征集之后,用其所有特征训练
LR模型。如果与前一组相比,验证集性能下降,则程序终止。 - 最大特征数:用户可以给出最大交叉特征数,这样当达到该数字时,
AutoCross停止。
- 运行时条件:用户可以设置
35.2 实验
数据集:来自
benchmark、以及真实世界商业数据集(来自第四范式的客户,经过脱敏),所有数据集都是二分类问题。数据集信息如下表所示。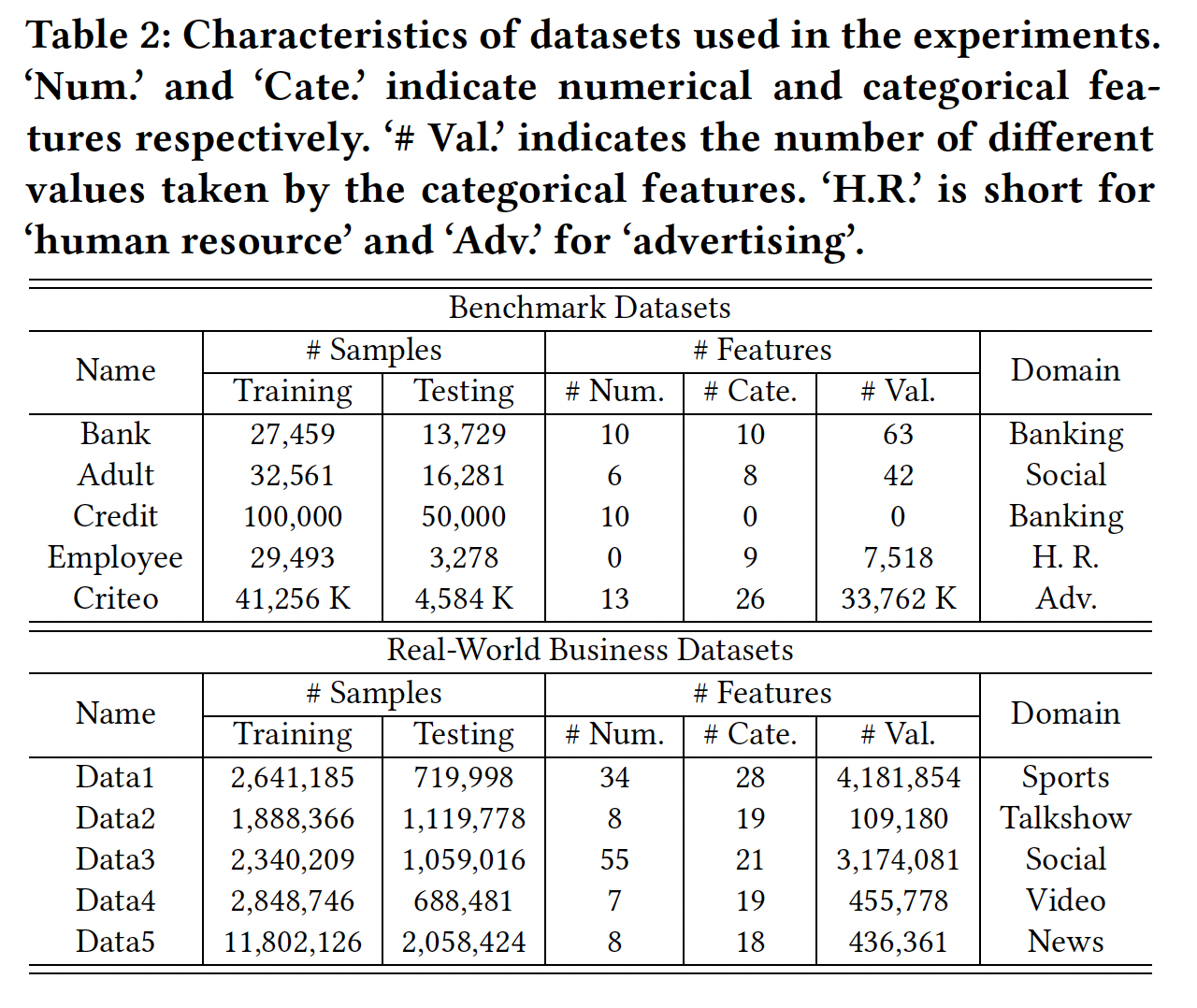
baseline方法:AC + LR:具有AutoCross生成的交叉特征的逻辑回归。AC+W&D:Wide & Deep模型,其中wide侧使用AutoCross生成的交叉特征。LR (base):采用原始特征的逻辑回归,作为baseline。CMI+LR:具有交叉特征的逻辑回归,其中交叉特征通过《Simple and scalable response prediction for display advertising》中提出的方法来生成,采用条件互信息(conditional mutual information : CMI)用作评估特征的指标。Deep:具有embedding layer的深度模型,它隐式地生成特征交互。xDeepFM:通过compressed interaction network: CIN显式生成特征的、SOTA的deeplearning-based方法。
在这些方法中,
AC+LR和AC+W&D使用AutoCross生成的交叉特征,并证明了其增强线性模型和深度模型的有效性。CMI+LR使用了一种典型的基于搜索的特征交叉方法。xDepFM是遵从Wide&Deep框架的SOTA方法。所有这些方法都旨在处理具有categorical feature的表格数据。配置:特征以及模型在训练数据集、验证数据集(如果需要的话,为训练数据的
20%)上学习,然后通过测试AUC来评估不同方法的性能。AutoCross配置:超参数包括数据块数量- 对于相对较小的数据集,即
Bank, Adult, Credit, Employee,50%的训练数据将用于连续小批量梯度下降。对于其他数据集,20%的采样率。 - 关于粒度级别,
AutoCross对所有数据集使用 - 至于终止条件,我们只调用性能条件,即只有在新添加的交叉特征导致性能下降时,
AutoCross才会终止。
- 对于相对较小的数据集,即
逻辑回归配置:超参数包括学习率
L1正则化系数L2正则化系数在我们的实验中,我们在特征生成之前调用了一个超参数调优过程,采用
log-grid search。找到的最佳超参数应用于所有LR相关的模型。CMI+LR配置:我们只在benchmark数据集上测试CMI+LR,因为CMI无法处理多值categorical feature。我们使用多粒度离散化来转换数值特征。为了确保特征评估的准确性,我们使用所有训练数据来估计CMI,Criteo数据集是一个例外,我们将其降采样比率设置为10%。我们将最大交叉特征数设置为15。深度模型配置:我们使用
xDeepFM的开源实现并在AC+W&D和Deep方法中使用深度组件。我们使用0.001学习率,Adam优化器,batch size = 4096,0.0001的L2正则化惩罚。深度组件的layer的隐单元数量为400。对于Criteo数据集和其它数据集,CIN组件分别采用200和100的隐单元数量。field embedding size = 10。由于在
xDepFM和Deep中不需要验证数据,因此我们不拆分训练集,并将其全部用于模型训练。
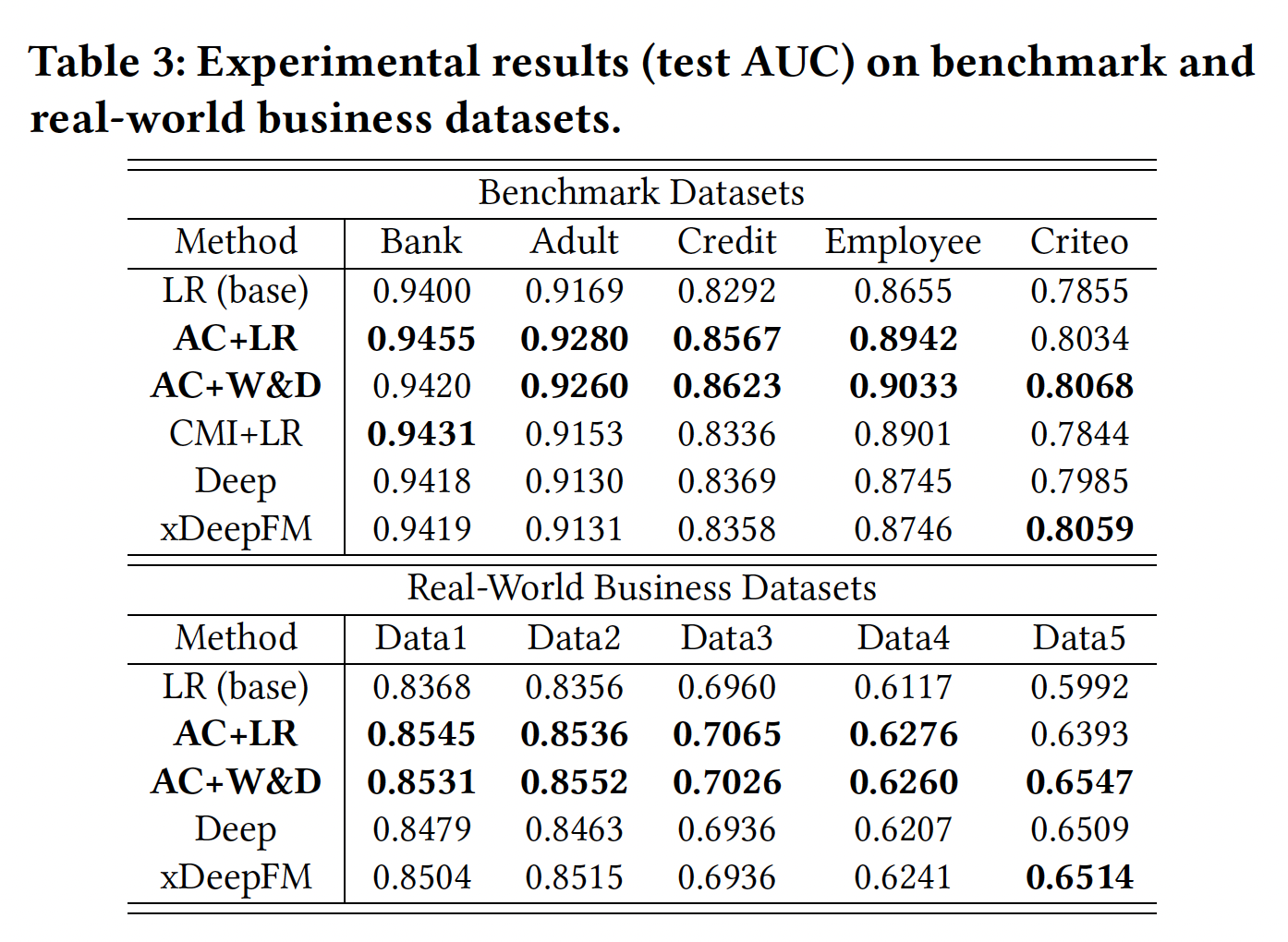
效果:实验结果如下表所示,其中我们突出显示了每个数据集的前两个方法。可以看到:
AC+LR在大多数情况下排名前二,并且通常优于基于深度学习的方法(Deep和xDepFM)。AC+W&D还显示出具有竞争力的性能,展示了AutoCross增强深度模型的能力。- 大多数情况下,
AC+LR和AC+W&D显示出比xDepFM更好的结果。
下表显示了
AutoCross带来的测试AUC改善。可以看到:AC+LR和AC+W&D都实现了比LR(base)显著的改进,并且AC+W&D也显著提高了Deep模型的性能。这些结果表明,通过生成交叉特征,AutoCross可以使数据更informative和discriminative,并提高学习性能。AutoCross取得的有前景的结果也证明了field-wise LR识别有用交叉特征的能力。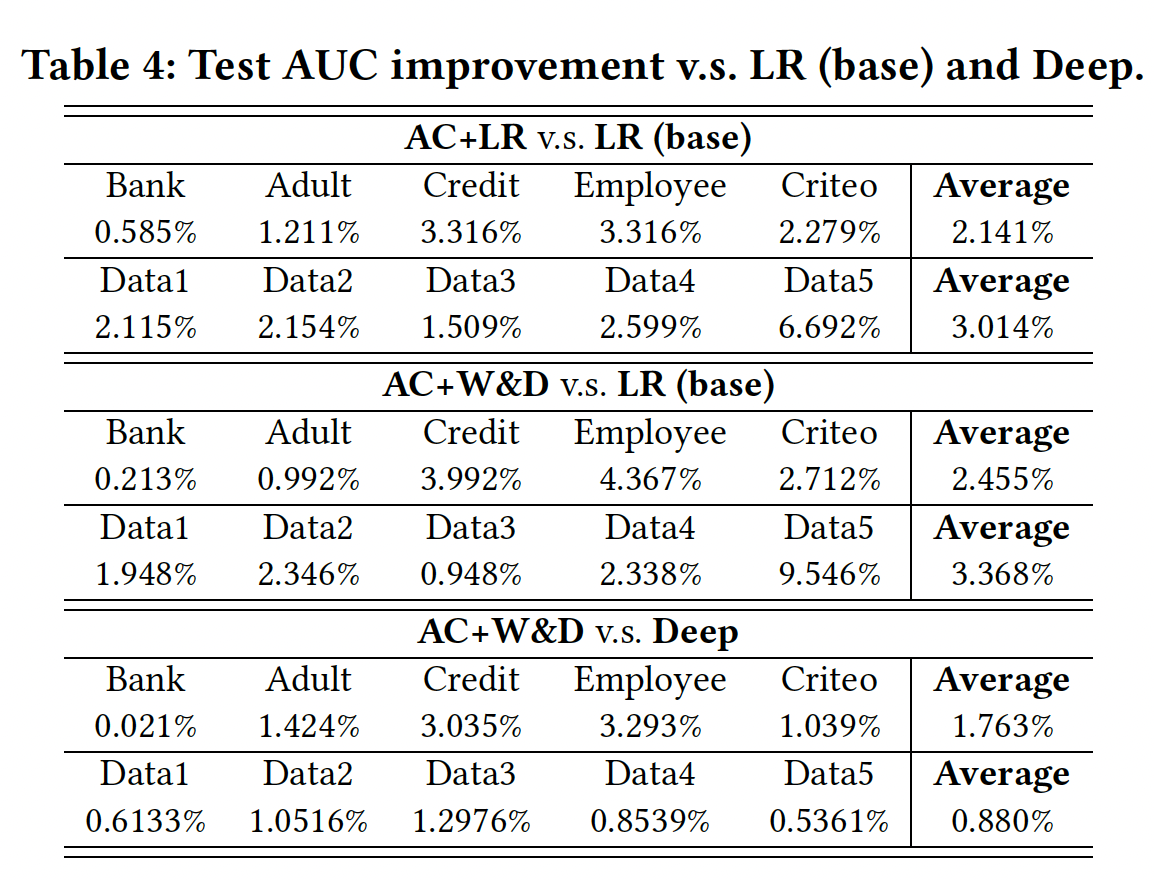
高阶特征的效果:下图显示了为每个数据集生成的二阶/高阶交叉特征的数量,其中后者占相当大的比例。
此外,在下表中,我们比较了仅生成二阶交叉特征的
CMI+LR、以及考虑高阶交叉特征的AC+LR。我们可以看到,AC+LR稳定且持续地优于CMI+LR。这一结果证明了高阶交叉特征的有用性。
特征交叉的时间代价:下表报告了
AutoCross在每个数据集上的特征交叉时间。下图显示了真实世界业务数据集上验证AUC(AC+LR)与运行时的关系。用户可以看到这些曲线,并随时终止AutoCross以获得当前结果。是在什么硬件配置下测试的?论文提到,
AutoCross采用PS架构,因此这里用到了几个parameter server、几个worker?值得注意的是,由于
AutoCross的高度简单性,不需要微调任何超参数,用户也不需要花费任何额外的时间来实现它。相比之下,如果使用基于深度学习的方法,则将在网络架构设计和超参数调优上花费大量时间。
推断延迟:在线推理包括两个主要步骤:生成特征从而转换输入数据、推理以进行预测。深度学习方法结合了这些步骤。在下表中,我们报告了
AC+LR、AC+W&D、Deep和xDepFM的推断时间。可以看到:AC+LR在推断方面比其他方法快几个数量级。这表明,AutoCross不仅可以提高模型性能,还可以确保其feature producer的快速推理。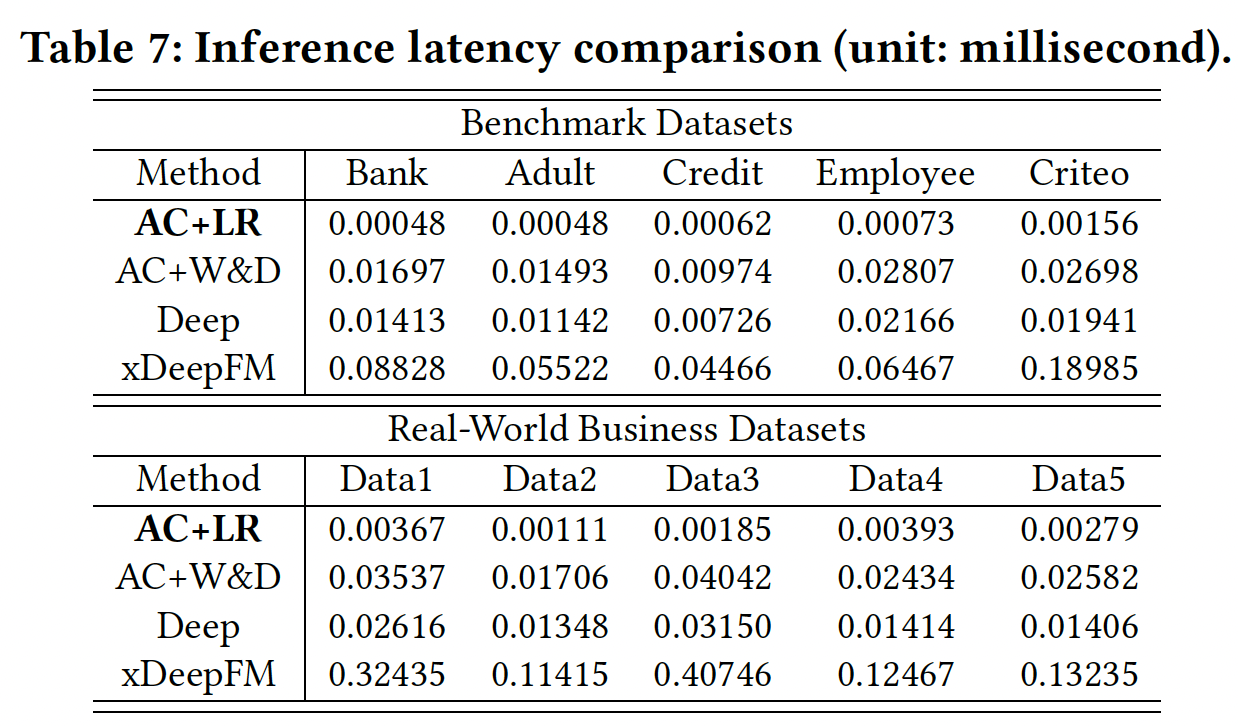
三十六、InterHAt[2020]
现有
CTR预测模型的架构复杂度和计算复杂度一直在增加,以便学到多个特征的联合效应,即高阶特征(也叫做交叉特征),并获得更好的预测准确性。具体而言,然而,不断增长的模型复杂度有两个缺点:可解释性差、效率低。
就可解释性而言,预测过程很难得到合理的解释,因为神经网络层的权重和激活
activation通常被认为是不可解释的。例如,Wide&Deep的Wide组件将叉积变换cross-product transformation应用于feature embedding,但未能量化和证明其对实际点击率预测性能的有效性。模型预测缺乏令人信服的理由,这给模型的可靠性和安全性蒙上了阴影。就效率而言,现有方法的效率低,因为深度神经网络的高阶交互特征的生成涉及
DNN中极其繁重的矩阵计算。例如,xDeepFM中的compressed interaction network: CIN通过一个外积层和一个全连接层来计算第embedding维度的立方复杂度。Wide&deep中的Deep组件具有多个全连接层,其中每个全连接层都涉及矩阵乘法。在实际应用中,效率问题是普遍而关键的。利用现有方法,学习大量现有特征、或新兴特征的
representation在计算上可能是难以处理的。
除了可解释性和效率问题,论文
《Interpretable Click-Through Rate Prediction through Hierarchical Attention》还指出了另一个障碍:模型会影响重要的交叉特征的评估。不同的交叉特征可能对CTR具有冲突的影响,必须全面分析。例如,电影推荐记录movie.genre = horror, user.age = young, time = 8am具有冲突的因素:前两者的组合鼓励点击,而后两者的组合抑制点击(因为电影观看通常发生在晚上)。这种冲突问题是由特征交互在不同语义子空间中的多义性引起的。在这个例子中,当user.age=young与两个不同的属性movie.genre和time组合时,user.age的多义性交互对CTR产生相反的影响。然而,这个问题在很大程度上被现有的方法所忽略。为了解决上述问题,在论文
《Interpretable Click-Through Rate Prediction through Hierarchical Attention》中,该论文提出了一个Interpretable CTR prediction model with Hierarchical Attention: InterHAt模型。InterHAt模型以端到端的方式有效地学习不同阶次的显著特征作为解释性的洞察,并同时准确地预测CTR。具体而言,
InterHAt通过一种新颖的hierarchical attention机制显式地量化任意阶次的特征交互的影响,聚合重要的特征交互以提高效率,并根据学到的特征显著性来解释推荐决策。与《Hierarchical attention networks for document classification》的研究语言的hierarchy(单词和句子)的hierarchical attention network不同,InterHAt对特征阶次采用hierarchical attention,高阶特征是在低阶特征的基础上生成的。为了适应特征交互在不同语义子空间中的多义性,
InterHAt利用具有multi-head self-attention的Transformer来全面研究不同的潜在特征交互。作者利用Transformer来检测特征交互的复杂多义性,并学习一个多义性增强的feature list,该列表用作hierarchical attention layer的输入。论文贡献如下:
- 论文提出使用
InterHAt进行CTR预测。具体而言,InterHAt采用hierarchical attention来精确定位对点击有很大贡献的重要的单个特征、或不同阶次的交互特征。然后,InterHAt可以基于各阶特征交互为CTR预测组成attention-based解释。 InterHAt利用具有multi-head self-attention的Transformer,从而在不同潜在语义子空间中彻底分析特征之间可能的交互关系。据作者所知,InterHAt是第一个方法使用具有multi-head self-attention的Transformer来学习潜在特征的多义性,从而以进行CTR预测。InterHAt预测CTR时无需使用需要大量计算成本的深层MLP。相反,它聚合了特征,因此节省了枚举指数级数量的特征交互的指开销。因此,它在处理高阶特征方面比现有算法更有效。- 在三个主要的
CTR基准数据集(Criteo, Avazu, Frappe)、一个流行的推荐系统数据集(MovieLens-1M)和一个合成数据集上,论文进行了大量的实验来评估InterHAt的可解释性、效率和有效性。结果表明,InterHAt解释了决策过程,在训练时间上实现了巨大的改善,并且仍然具有与SOTA的模型相当的性能。
相关工作:
CTR预测模型:FM为每个不同特征分配一个embedding向量 ,并通过一阶特征和二阶特征的线性组合来进行预测。虽然FM可以推广到高阶情况,但高阶FM的计算复杂度为指数级,并且浅层架构的模型容量较低。Field-aware Factorization Machine: FFM假设特征在不同的field下可能具有不同的语义,并通过field-specific feature representation来扩展FM的思想。虽然它获得了比FM更好的效果,但是也增加了参数规模和计算量,并且更容易发生过拟合。Attentional Factorization Machine: AFM通过attention net扩展了FM,不仅提高了性能,还提高了可解释性。然而,由于FM固有的结构限制,AFM只能学习二阶特征交互。Wide&Deep由wide组件和deep组件构成,它们本质上分别是广义线性模型和MLP。注意,deep组件,即MLP,破坏了可解释性,因为layer-wise transformation是在unit level而不是feature level进行的,并且单个unit level取值不能携带特征的具体的、完整的语义信息。Deep&Cross Network: DCN与Wide&Deep略有不同,因为DCN用叉积变换取代了线性模型,从而将高阶信息与非线性深度特征相结合。DeepFM通过用FM作为wide组件来改进这两个模型,其中deep MLP组件捕获高阶特征交互,wide FM捕获二阶特征交互。xDeepFM声称MLP实际上是建模隐式特征交互,因此作者引入compressed interaction network: CIN来建模显式特征交互。- 工业实践的最新成果包括
DIN和DIEN,它们分别建模用户的静态购物兴趣和动态购物兴趣。这两种方法都严重依赖于深度前馈网络,而这种网络通常是不可解释的。
所有上述
CTR预测模型都严重依赖于深度神经网络,并实现不断提高的性能。然而,正如一把双刃剑,深度学习算法在可靠性和安全性方面存在潜在风险。隐层的权重和激活activation很难解释,输入和输出之间的因果关系是掩藏的、不确定的。它们都没有提供任何feature-level的线索来解释为什么这种深度feature learning策略会增强或减弱CTR性能。相反,
InterHAt在feature-level上使用attention-based的解释来解决CTR预测。也就是说,InterHAt没有不合理的深度MLP模块,并且InterHAt仅工作在feature level上,这也提高了InterHAt的效率。attention机制:attention机制最初是为neural machine translation: NMT提出的,它为源语言和目标语言之间密切相关的单词分配更大的权重,以便在翻译中关注重要的单词。NLP中另一种形式的attention是自注意力,如Transformer架构。我们采用注意力机制来解释InterHAt模型的CTR预测。
36.1 模型
InterHAt模型的整体架构如下图所示。Transformer with Multi-head Self-attention可以视为是单个交互层的AutoInt模型。实验部分表明,该组件很重要,移除该组件会导致模型性能较大的下降。但是,实验部分并没有比较InterHAT和AutoInt的比较,因为二者都宣称是可解释的,并且InterHAT将AutoInt作为组件。Attentional Aggregation Layer通过自注意力机制来获得不同阶次的、聚合所有field信息的representation向量,并将其用于预测和可解释。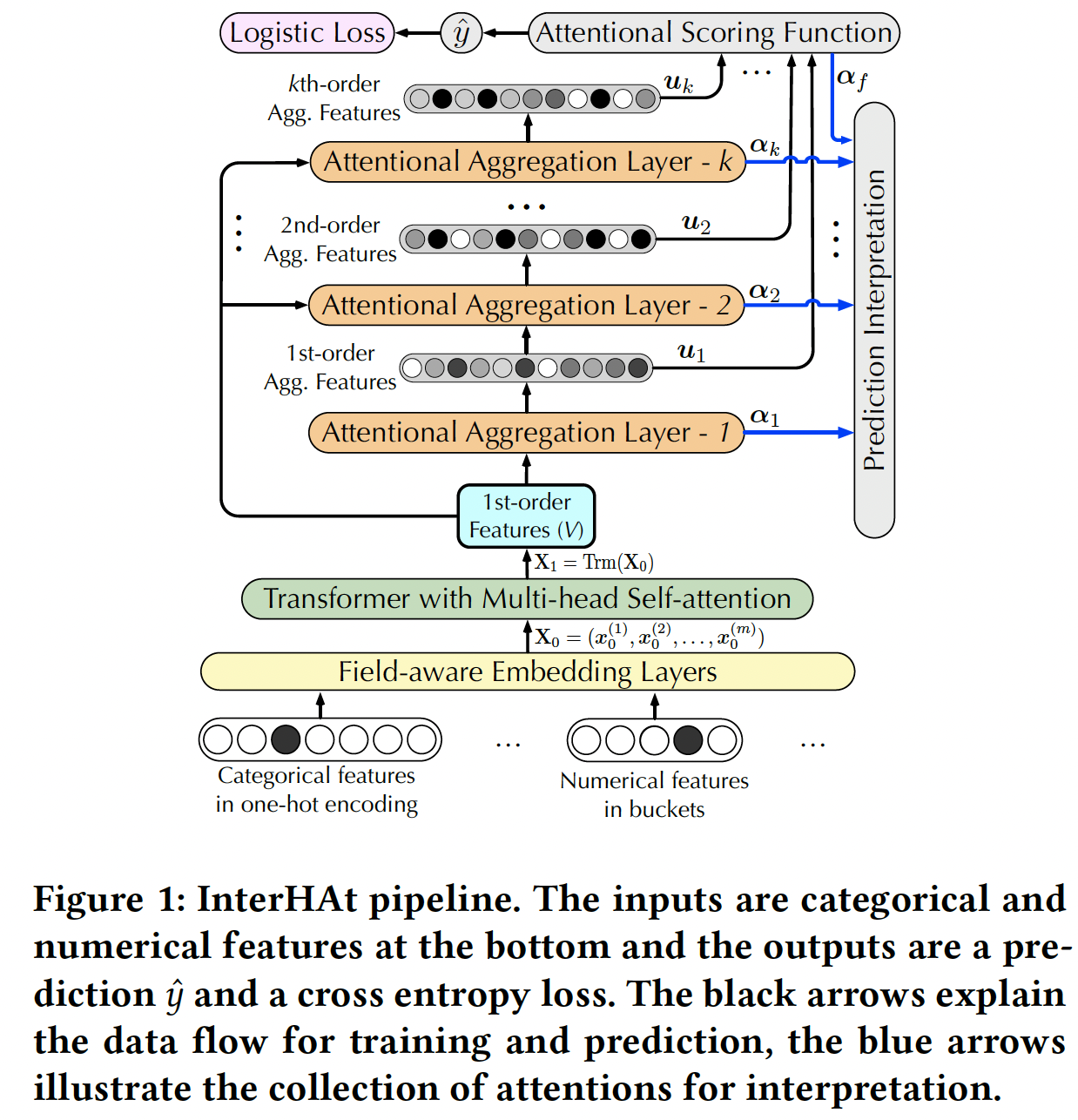
Embedding Layer:输入特征包含一组fieldfieldcategorical的、要么是numerical的。- 对于
categorical field,每个categorical valueembeddingcategorical fieldfield的的representationemebdding,即 - 对于
numerical field,我们为每个field分配一个可训练的embedding。令fieldfield分配的embedding,那么该field的representation为
考虑所有的
field,定义初始的input representation matrix为:其中:
field数量。- 对于
Multi-head Transformer:在CTR预测任务重,我们将特征朝着不同极性(消极或积极)的协同效应(即,特征交互)定义为多义性polysemy。因此,我们为InterHAt采用了一个Multi-head Transformer从而捕获丰富的pair-wise特征交互,并且学习不同语义子空间中特征交互的多义性。给定输入矩阵
Transformer headrepresentation其中:
head的维度。hidden featureaugmented representation matrixReLU的前馈层从而学习非线性:其中:
head数量,“embedding维度)。Hierarchical Attention:augmented representation matrixhierarchical attention layer的输入。hierarchical attention layer学习特征交互并同时产生解释。然而,由于组合爆炸,通过枚举所有可能的组合来计算高阶multi-feature interaction是昂贵的。因此,我们在计算更高阶次的特征交互之前,首先聚合当前阶次的特征交互。即,为了生成第其中:
field在第attentional aggregation layer的注意力权重;layer weight;gated attention mechanism。这里采用的是自注意力机制。
然后我们根据
其中:
Hadamard product。根据
- 第
- 第
1层的第self-attention的权重。
那么,是否可以用
query向量从而用传统的注意力机制来计算最后,模型预测时利用的是
通过一系列的
attentional aggregation layer,我们得到了从第1 ~ k阶的交叉特征。这些层组成了一个hierarchy,表示从低阶到高阶所抽取的特征。最后,我们联合所有的
attentional aggregation- 第
目标函数和优化:最终的预测函数为
其中:
目标函数为交叉熵:
其中:
L2正则化系数。我们采用
Adam优化器来优化目标函数。可解释性:我们使用注意力分布
CTR预测结果的重要因素,其中:final attentional aggregation layer的注意力分布,其中的top权重确定了那些阶次的交叉特征attentional aggregation layer的注意力分布,其中的top权重决定了哪些单个feature field
注意,注意力机制仅突出了特征的显著性,因此不期望它生成完全人类可读的解释。
最后,根据上述步骤,我们可以识别不同阶次的所有特征。对点击行为的解释是通过逐层地、逐阶次地识别显著特征来解释的。
36.2 实验
数据集:
Criteo, Avazu, Frappe。下表展示了数据集的统计信息,其中训练集/验证集/测试集的大小之比为8:1:1。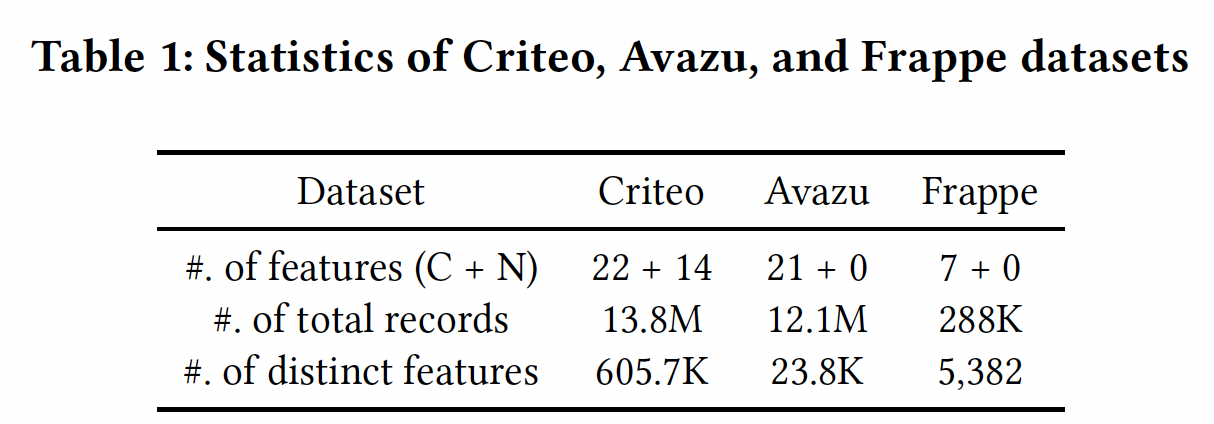
baseline方法:FM:通过一阶特征和二阶特征(feature embedding向量的内积)的线性组合来进行预测CTR。Wide&Deep:广义线性模型和deep MLP的ensemble。DCN:用于计算高阶特征的cross-product transformation、以及deep MLP的ensemble。PNN:基于乘积的方法,它的架构由简单的内积、外积、以及非线性激活函数所组成。DeepFM:FM和deep MLP的组合。xDeepFM:显式建模特征交互的compress information network: CIN、以及deep MLP的组合。
评估指标:
Logloss, AUC。实现:
InterHAt是通过Python 3.7 + TensorFlow 1.12.0实现的,在单个16GB Nvidia Tesla V100 GPU上运行。默认的超参数如下: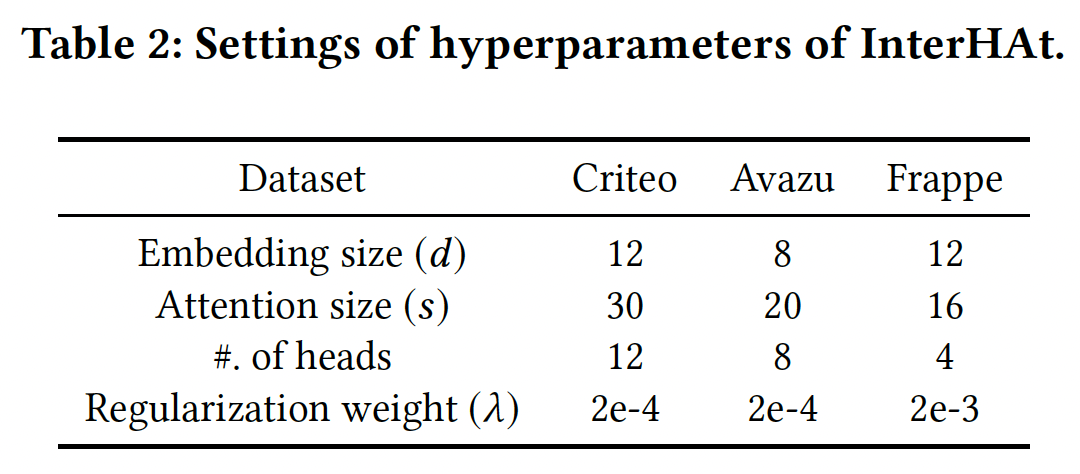
36.2.1 实验结果
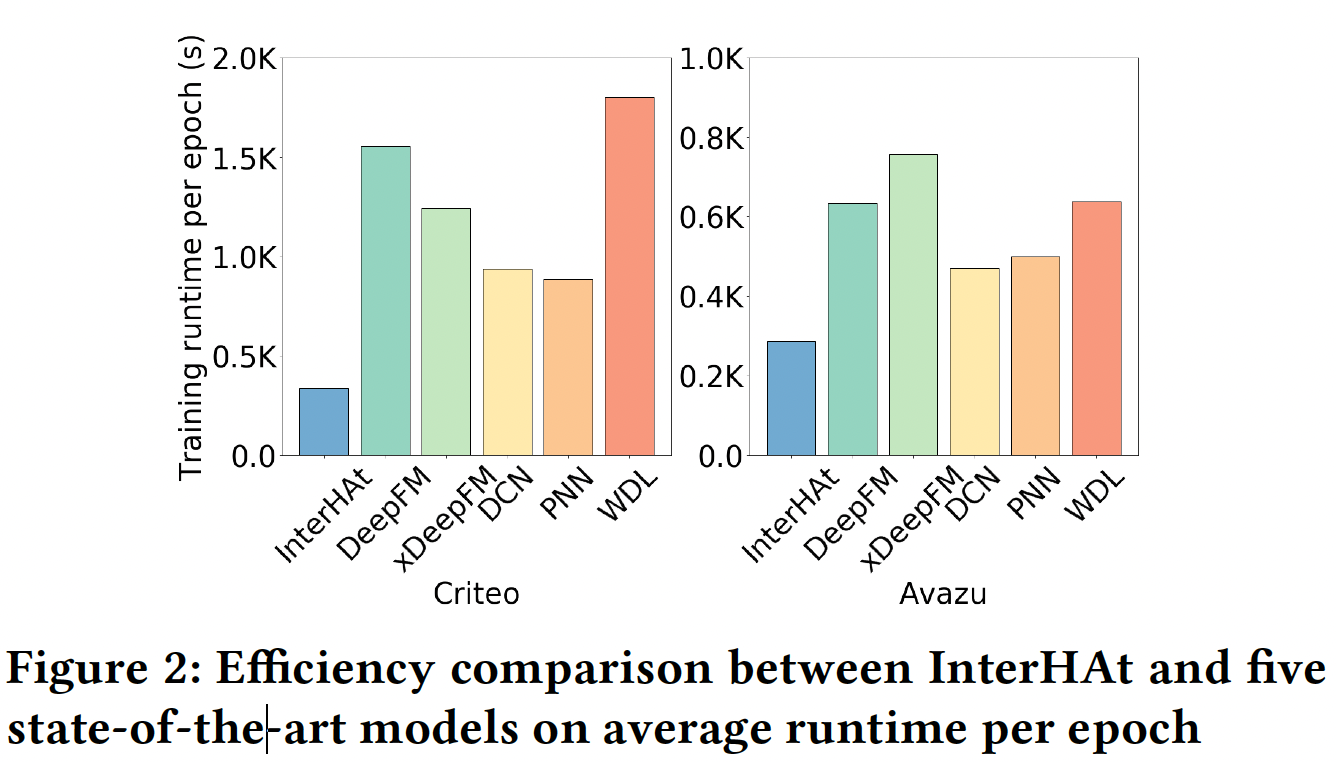
效率测试:下图展示了在
Criteo和Avazu上不同模型之间的运行时间比较。Frappe不用于效率测试,因为它的数据集规模相对较小。FM不参与比较,因为只有CPU-based实现可用,而其它模型都是GPU-based的。y轴显示了在五个训练epoch内,每个epoch的平均运行时间。可以看到:InterHAt在每个epoch上的训练时间最短,表现出了出色的效率。InterHAt的两个性质实现了巨大的加速:- 跨所有特征的
attentional aggregation操作通过避免在 - 与
baseline模型中使用的deep MLP相比,IntarHAt中仅涉及shallow MLP。深度神经网络由于庞大的参数规模而大大降低了计算速度。
- 跨所有特征的
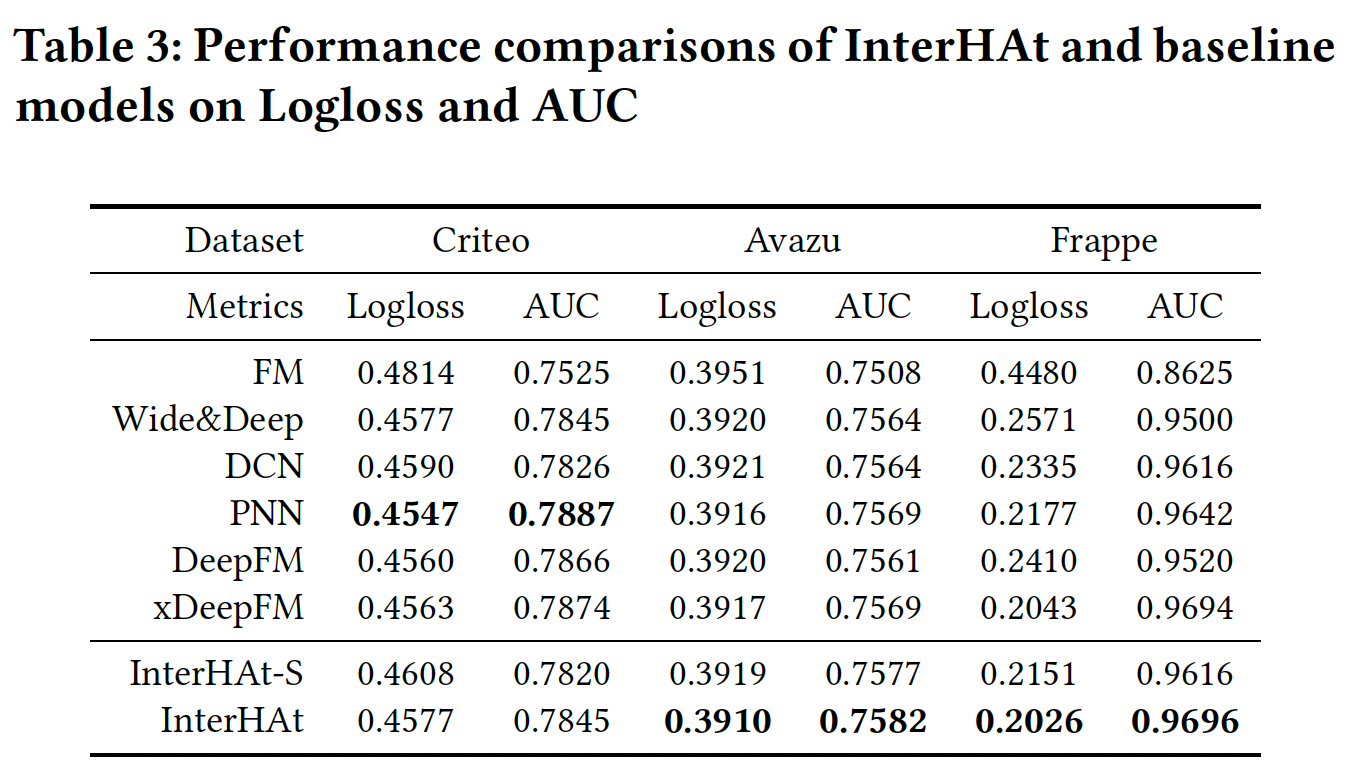
效果测试:不同模型的效果比较如下表所示。可以看到:
InterHAt在Frappe和Avazu数据集的所有两个指标上都优于所有模型,并在Criteo数据集上获得了可比的性能。然而,InterHAt的结构更简单。InterHAt-S指的是InterHAt的变体,它移除了multi-head self-attention模块。InterHAt-S性能的下降证明了Multi-head Transformer的贡献。
InterHAt在Criteo数据集上稍差的原因是:相比比
Avazu和Frappe数据集,Criteo的特征在语义上更复杂。best baseline模型使用不可解释的深度全连接层来捕获复杂的隐式信息并提高性能。然而,InterHAt没有使用损害可解释性的深度全连接层。此外,当前的
field-aware embedding策略(numerical field仅有单个embedding)破坏了numerical-numerical和categorical-numerical特征交互的能力。我们把对适当的feature representation方案的探索留给未来的工作。可以考虑和
AutoDis结合,从而自动离散化numerical feature。
Transformer head数量的敏感性:下图给出了不同head数量的InterHAt的效果。我们将head数量从1增加到12,保持其他setting不变,并训练模型直到收敛。可以看到:- 对于
Criteo和Avazu数据集,最佳head数量分别为8和4。 - 对于
Frappe数据集,最佳head数量为1。
这与我们的观察一致,即
Frappe field的语义彼此隔离,没有任何潜在的交互(即,每个field只有一个语义空间)。研究结果证明了复杂数据集的样本中存在特征多义性,并证明了
multi-head Transformer的有用性。随着
head数量的增加,模型性能会因过度参数化而下降。
- 对于
36.2.2 可解释性
在得到
CTR预测的同时,我们也得到了解释,这是InterHAt的主要贡献之一。这里我们通过可视化学到的、显著的低阶特征或高阶特征来演示可解释性。然而,Criteo和Avazu数据集中,field内容因为隐私保护问题而被加密,这使得无法证明由InterHAt构造的解释是否合理。为此,我们使用一个真实数据集、以及一个人工合成的数据。真实数据集:
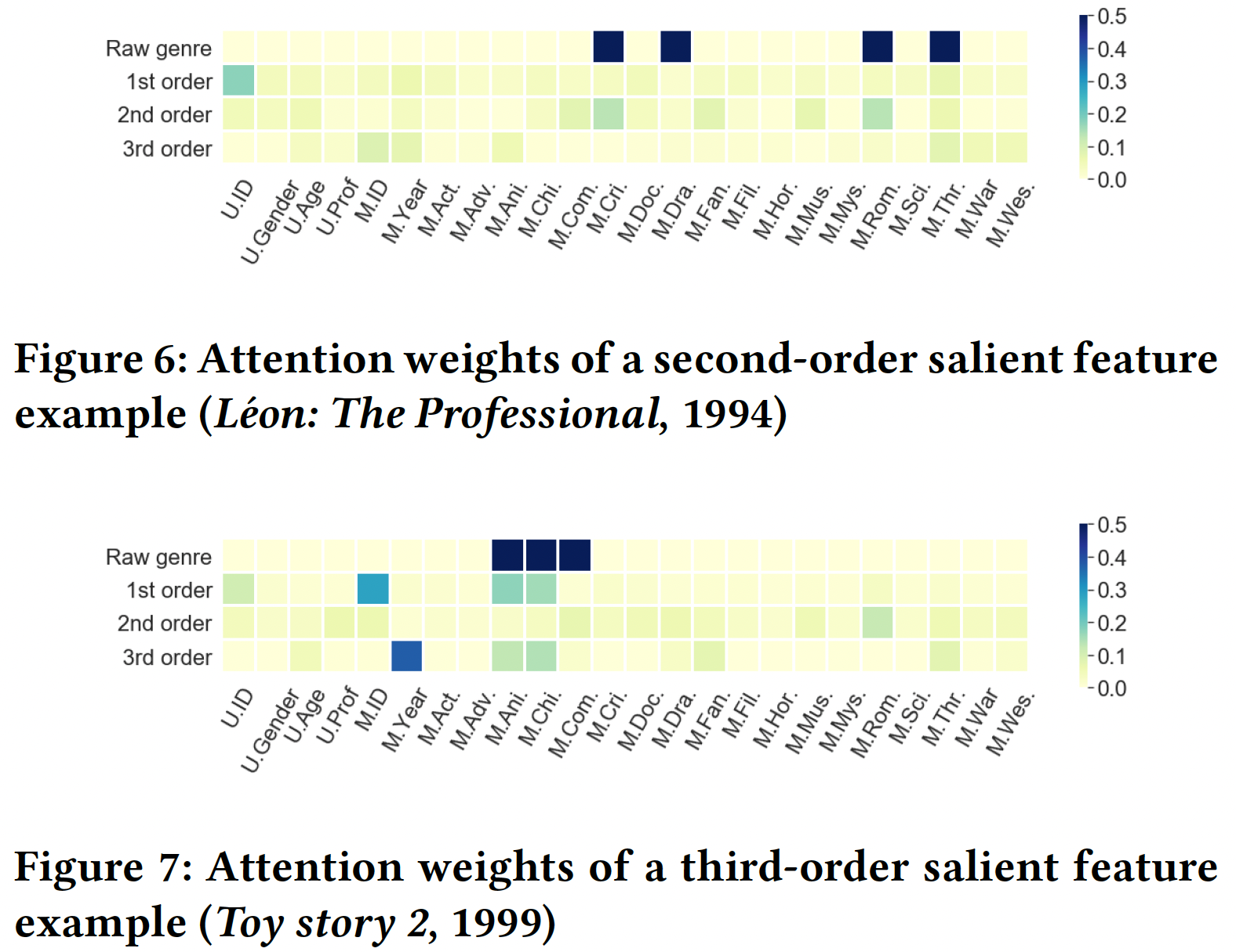
MovieLens-1M数据集,具有明文属性。每个样本都有用户画像、电影属性、以及1~5的评级。用户画像包括年龄、性别、职业,电影属性包括发型年份、电影风格(18种风格)。我们将评分动作视为点击,即label = 1的正样本,然后通过随机采样(movie, user) pair来创建与正样本数量相同的负样本。正样本和负样本没有重叠。我们绘制了从一阶到三阶注意力权重的热力图,即
Figure 5/6/7中,深色的cell表示InterHAt学到的更大的特征重要性。横轴为电影流派,被简写为三个字母。在Raw genre行,黑色的cell表示输入数据中包含对应的电影派别属性。Figure 5显示了对电影《终结者》(1984) 的可解释结果,该样本在Figure 6显示了对电影《Léon: The Professional (1994) 》的可解释结果,该样本在Figure 7显示了对电影《玩具总动员2 》(1999) 的可解释结果,该样本在

人工合成数据集:考虑到
MovieLens-1M是评级数据而不是点击数据,我们使用人工合成的点击数据集。合成数据包含10个fieldfield是独立创建的,并且取值空间全部都是label根据feature group来决定,其中feature group如下表所示:例如,对于第二条规则,当条件
label取值为1的概率为label取值为1的概率为0.9、0.2。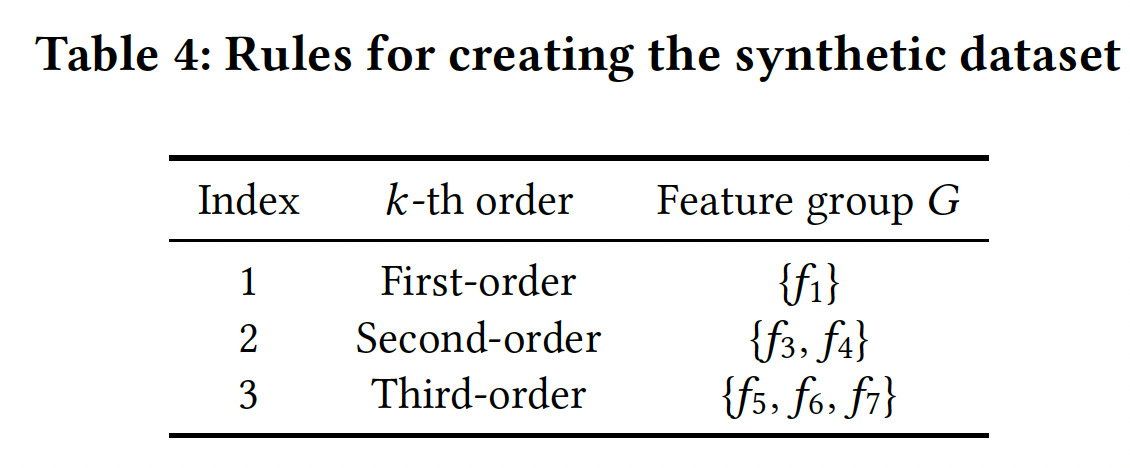
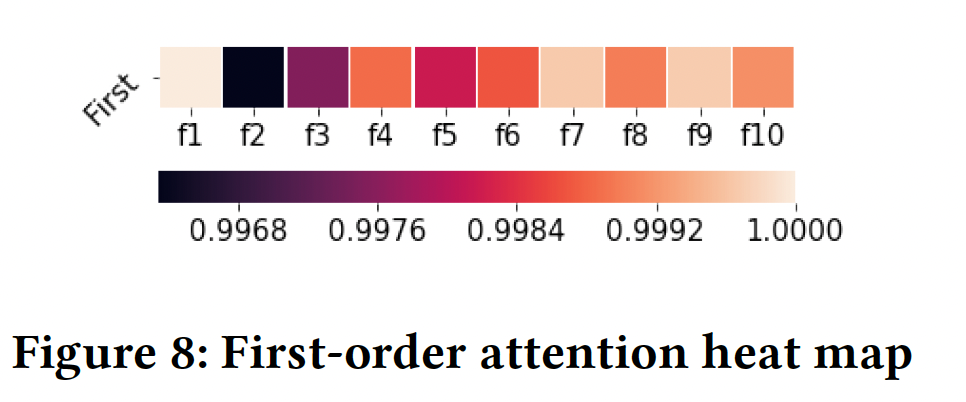
评估结果如下图所示。我们通过每一层中注意力的热力图来呈现显著的特征。以下热图中第
cell表示满足Table 4中的aggregation attentionFigure 8给出了所有样本的一阶热力图。我们观察到:Rule 1一致。- 此外,来自注意力的方差较小,这意味着仅使用一阶交互进行学习和预测时,稳定性较差。
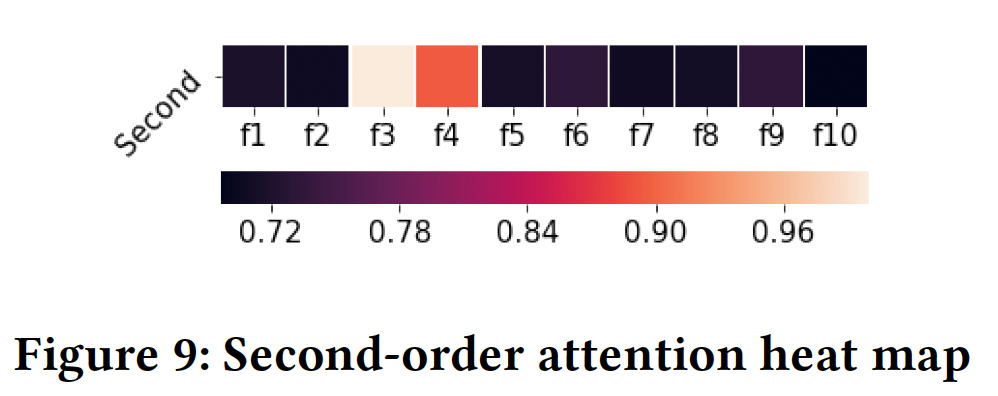
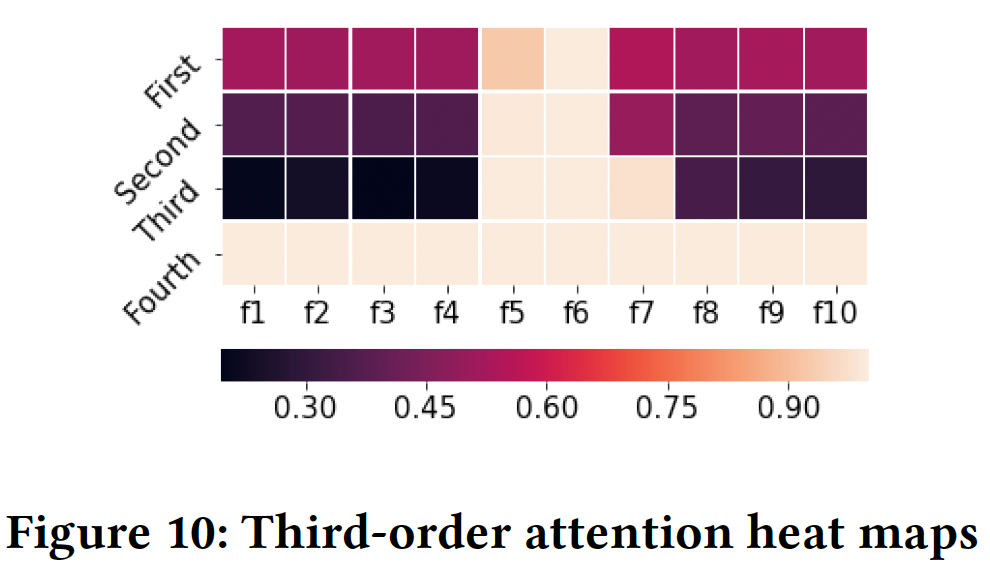
Figure 9给出了所有样本的二阶热力图。我们观察到Rule 2一致。Figure 10给出了所有样本的一阶到四阶热力图。我们观察到:- 在前三阶中,
- 在第四阶,所有
field具有均匀的注意力分布。这表明数据集中不存在更高阶的特征。
- 在前三阶中,
三十七、xDeepInt[2023]
在
CTR预测模型中,探索有用的特征交互在提高模型性能方面起着关键作用。传统上,数据科学家根据领域知识搜索和建立手工制作的特征交互,以提高模型性能。在实践中,高质量的特征交互需要昂贵的时间和人力成本。此外,鉴于大量的特征和高cardinality,手动提取所有可能的特征交互是不可行的。因此,在高维和稀疏的特征空间中,自动有效地学习低阶特征交互和高阶特征交互,成为学术界和工业界提高CTR预测模型性能的一个重要问题。由于强大的
feature learning能力,深度学习模型在推荐系统中取得了巨大的成功。学术界和工业界都提出了一些深度学习架构。然而,所有现有的模型都是利用DNN作为学习高阶的、隐式的、bit-wise特征交互的building block,没有阶次的约束。当建模显式的特征交互时,现有的方法只能有效地捕获低阶的显式交互。学习高阶交互通常需要更高的计算成本。在论文
《xDeepInt: a hybrid architecture for modeling the vector-wis eand bit-wise feature interactions》中,作者提出了一个高效的基于神经网络的模型,称为xDeepInt,以显式地学习vector-wise特征交互和bit-wise特征交互的组合。在多项式回归的启发下,作者设计了一个新颖Polynomial Interaction Network: PIN层来显式地捕捉有界阶次的vector-wise交互。为了以可控的方式同时学习bit-wise交互和vector-wise交互,作者将PIN与subspace-crossing机制相结合,这大大提升了模型性能,并带来更多的灵活性。bit-wise交互的阶次随着子空间的数量而增长。综上所述,论文贡献如下:
- 论文设计了一个名为
xDeepInt的新型神经网络架构,它显式地同时建模了vector-wise交互和bit-wise交互,免除了联合训练的DNN和非线性激活函数。所提出的模型是轻量级的,但是比许多现有的结构更复杂的模型产生了更好的性能。 - 在高阶多项式逻辑回归的启发下,论文设计了一个
Polynomial-Interaction-Network: PIN层,它可以递归地学习高阶的、显式的特征交互。通过调整PIN层的数量来控制交互的阶次。作者进行了一项分析,以证明PIN的多项式逼近的属性。 - 论文引入了一个
subspace-crossing机制来建模PIN层内不同field之间的bit-wise交互。PIN层和subspace-crossing机制的结合使我们能够控制bit-wise交互的阶次。随着子空间数量的增加,模型可以动态地学习更细粒度的bit-wise特征交互。 - 论文设计了一个与所提模型的结构相协调的优化策略。论文将
Group Lasso FTRL应用于embedding table,将整个行缩减为零,实现了feature selection。为了优化PIN层的权重,论文直接应用FTRL。权重的稀疏性导致了对特征交互的选择。 - 论文在三个真实世界的数据集上进行了综合实验。结果表明:
xDeepInt在极端高维和稀疏的setting下优于现有SOTA的模型。论文还对xDeepInt的超参数设置进行了敏感性分析,并对DNN的集成进行了消融研究。
- 论文设计了一个名为
相关工作:
建模隐式交互:大多数
DNN-based的方法在初始阶段将高维稀疏categorical feature和连续特征映射到低维潜在空间。在不设计具体模型结构的情况下,DNN-based的方法通过将stacked embedded feature vector馈入深度前馈神经网络来学习高阶的隐式的特征交互。Deep Crossing Network利用前馈结构中的残差层来学习高阶交互,并提高稳定性。- 一些混合网络架构,包括
Wide & Deep Network: WDL、Product-based Neural Network: PNN、Deep & Cross Network: DCN、Deep Factorization Machine: DeepFM、eXtreme Deep Factorization Machine: xDeepFM采用前馈神经网络作为其深度组件来学习高阶的隐式交互。补充的隐式高阶交互提高了那些仅仅建模显式交互的网络的性能。
建模显式交互:
Deep & Cross Network: DCN以显式的方式探索bit-wise level特征交互。具体而言,DCN的每个cross layer都构建了所有的交叉项,从而利用bit-wise交互。cross layer的数量控制了bit-wise特征交互的阶次。最近的一些模型使用向量乘积的特定形式显式地学习
vector-wise特征交互。Deep Factorization Machine: DeepFM通过联合学习feature embedding,将factorization machine layer和前馈神经网络结合起来。factorization machine layer通过内积pairwise vector-wise交互。然后,vector-wise输出与前馈神经网络的输出单元相拼接。Product Neural Network: PNN引入了内积层inner product layer和外积层outer product layer,分别学习显式的vector-wise交互和显式的bit-wise交互。是否可以用类似于
AutoFIS的机制,在搜索阶段查找vector-wise交互和bit-wise交互中的重要交互,然后在重训练阶段裁剪掉不重要的交互从而提高性能?xDeepFM通过使用Compressed Interaction Network: CIN学习显式的vector-wise交互,其中CIN具有类似于RNN的架构,并使用Hadamard product学习所有可能的vector-wise交互。卷积滤波器和池化机制被用来提取信息。FiBiNET利用Squeeze-and-Excitation网络动态地学习特征的重要性,并通过双线性函数来建模特征交互。
在最近关于序列模型的研究中,
Transformer架构被广泛用于理解相关特征之间的关联。通过不同层的多头自注意力神经网络,AutoInt可以学习输入特征的不同阶次的特征组合。一些工作采用残差连接从而传递不同阶次的特征交互。
上述方法通过使用外积、
kernel product、或多头自注意力来学习显式的特征交互,这需要昂贵的计算成本。
37.1 模型
xDeepInt的架构如下图所示:- 首先是输入层和
embedding层,它们将连续特征和高维categorical feature映射到一个稠密的向量。 - 然后是
Polynomial Interaction Network: PIN层,它们利用带残差连接的交互层来显式地学习vector-wise交互。 - 此外我们实现了
subspace-crossing机制来建模bit-wise交互,其中子空间的数量控制着bit-wise交互的和vector-wise交互的混合程度。
论文的核心思想就是
DCN V2加上subspace-crossing机制。其中subspace-crossing机制会大大增加模型容量,介于feature-wise和bit-wise之间。论文整体创新性不足,不建议阅读。此外,
subspace-crossing机制可以在实践中应用。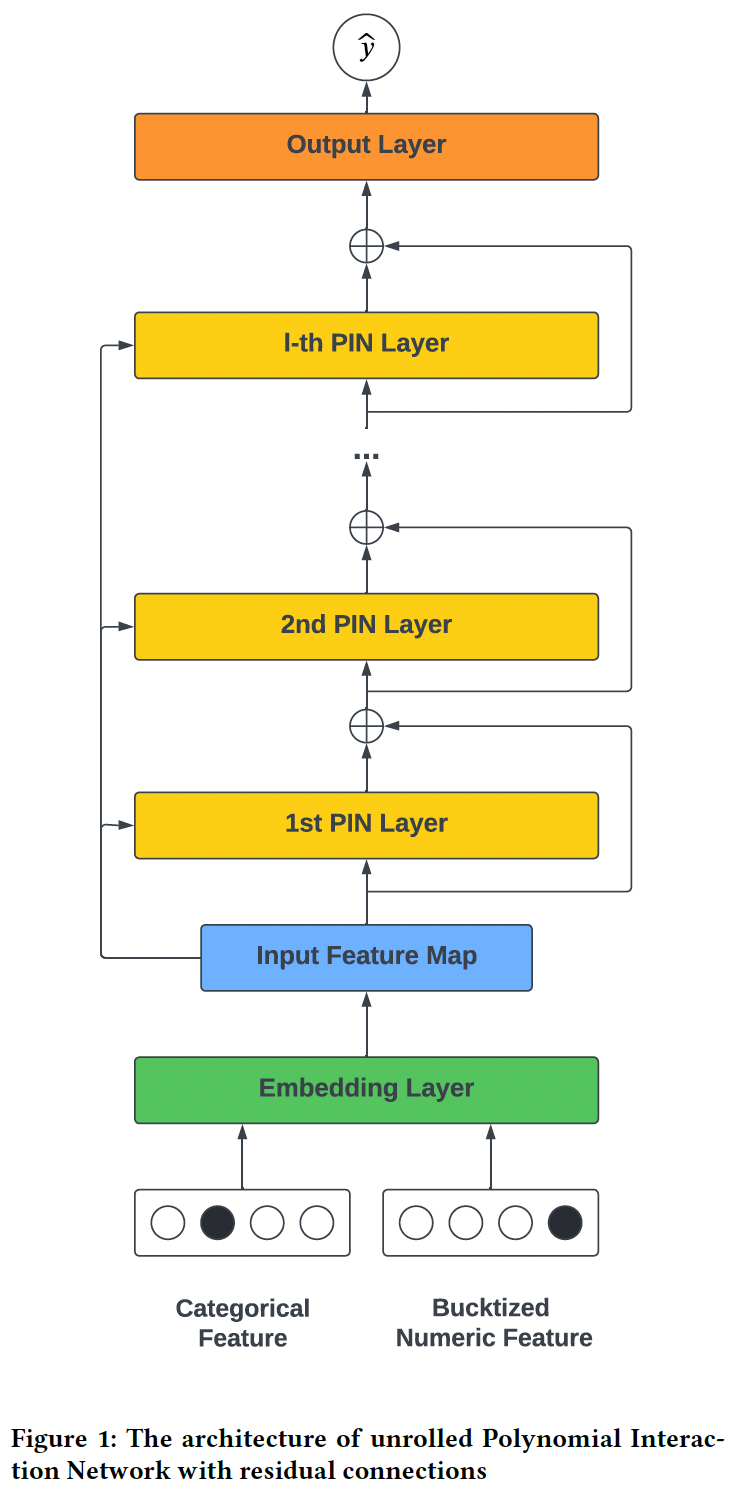
- 首先是输入层和
Embedding Layer:假设我们有field。在我们的特征预处理步骤中,我们将所有的连续特征以equal frequency bin的方式分桶,然后将分桶后的连续特征、以及categorical特征嵌入到同一个潜在空间其中:
fieldembedding matrix,fieldone-hot向量(即,原始的输入特征),fieldembedding向量。我们堆叠
embedding向量,从而获得input feature map注意:大多数
DNN-based方法将embedding向量拼接成一个更长的一维向量,而这里将embedding向量堆叠为二维矩阵。Polynomial Interaction Network: PIN:PIN的公式如下:其中:
Hadamard product;上述公式就是
DCN V2的公式。第
PIN层的输出,是所有阶次小于等于vector-wise交互的加权和。PIN层的结构是根据以下几个方面启发而来:- 首先,
PIN有一个递归结构。当前层的输出建立在上一层的输出、以及一阶feature map的基础上,确保高阶特征交互是建立在前几层的低阶特征交互之上。 - 其次,我们使用
Hadamard product来建模显式的vector-wise交互。相比内积的形式,Hadamard product保留了更多的信息。 - 然后,我们建立一个
field aggregation layervector-wise level上使用线性变换feature map。field aggregation feature map的每个向量可以被看作是由input feature map的加权和所构建而成。 - 然后,针对当前层,我们取
field aggregation feature map以及上一层输出之间的Hadamard product。这一操作使我们能够在现有的 - 最后,我们利用残差连接,从而允许组合不同阶次的
vector-wise的特征交互,包括第一个feature map。随着层数的增加,特征交互的阶次也在增加。PIN的递归结构能够限制多项式特征交互的阶次。
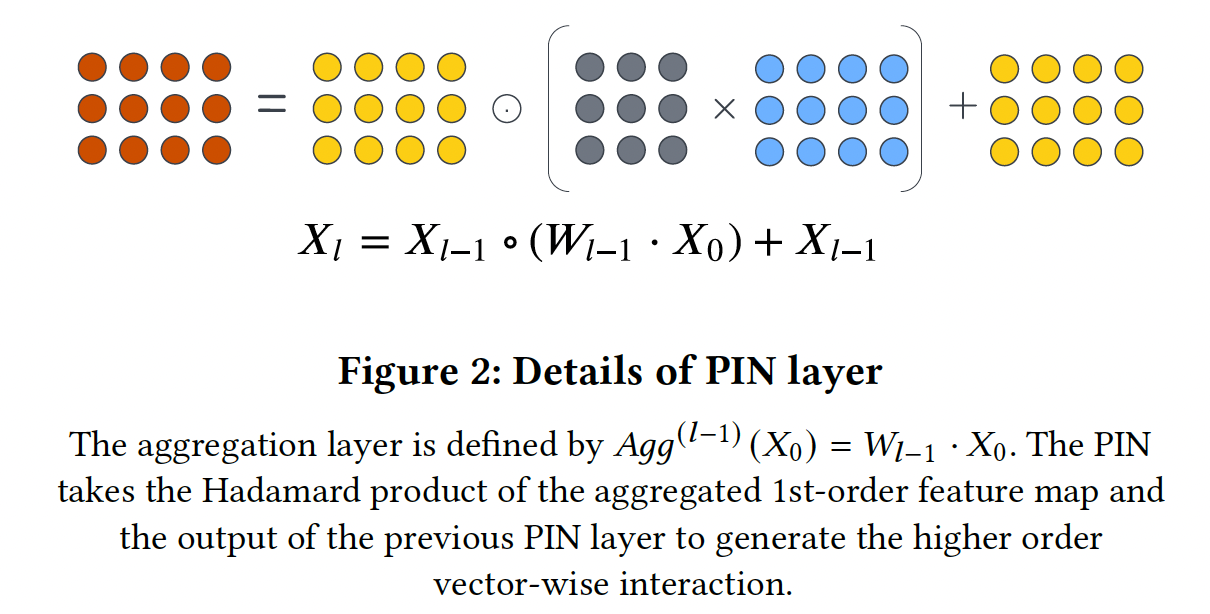
- 首先,
subspace-crossing机制:PIN建模vector-wise交互,然而它无法建模bit-wise交互。为了建模bit-wise交互,我们提出了subspace-crossing机制。假设我们把embedding空间拆分为input feature map其中:
然后,我们在
field维度上堆叠所有子矩阵,并构建一个堆叠的input feature map:通过将每个
field的embedding向量分割成embedding维度的bit进行对齐,并在堆叠的sub-embedding上创建vector-wise交互。因此,我们将PIN:其中:
在普通的
PIN层中,feature map的field aggregation、Hadamard product的乘法交互都是vector-wise level的。subspace-crossing机制所增强的PIN将PIN通过交叉不同子空间的特征来捕获显式的bit-wise交互。子空间的数量bit-wise交互的复杂性,较大的这其实是
group-bit wise的交互,而不仅仅是bit-wise交互。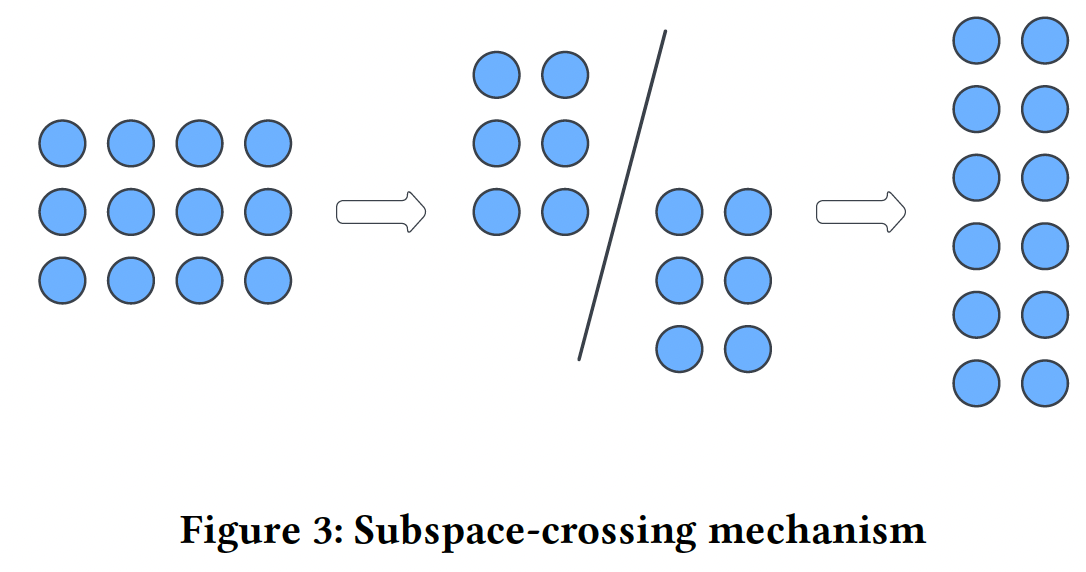
Output Layer:PIN的输出是一个由不同阶次的特征交互组成的feature map,包括由残差连接保留的原始input feature map、以及由PIN学到的高阶特征交互。最终预测为:其中:
sigmoid函数,feature map聚合向量,bias。优化和正则化:我们使用
Group Lasso Follow The Regularized Leader: G-FTRL作为embedding层的优化器从而进行特征选择。我们使用Follow The Regularized Leader: FTRL作为PIN层的优化器从而进行交互选择。Group lasso FTRL将每个field中不重要的特征的整个embedding向量正则化为完全为零,这实质上是进行特征选择,并且为工业界的setting带来更多的训练效率。group lasso regularization是在子空间分割机制之前应用的,这样特征选择在每个子空间之间是一致的。FTRL将PIN层中weight kernel的单个元素正则化为完全为零,这就排除了不重要的特征交互,使模型的复杂性正则化。 这种优化策略利用了不同优化器的特性,在embedding table和weight kernel中分别实现了row-wise稀疏性和element-wise稀疏性。因此,它同时提高了training和serving的泛化能力和效率。它在模型压缩方面也发挥了重要作用。
如果换
Adam优化器,那么最终性能有所下降,但是仍然保持较好。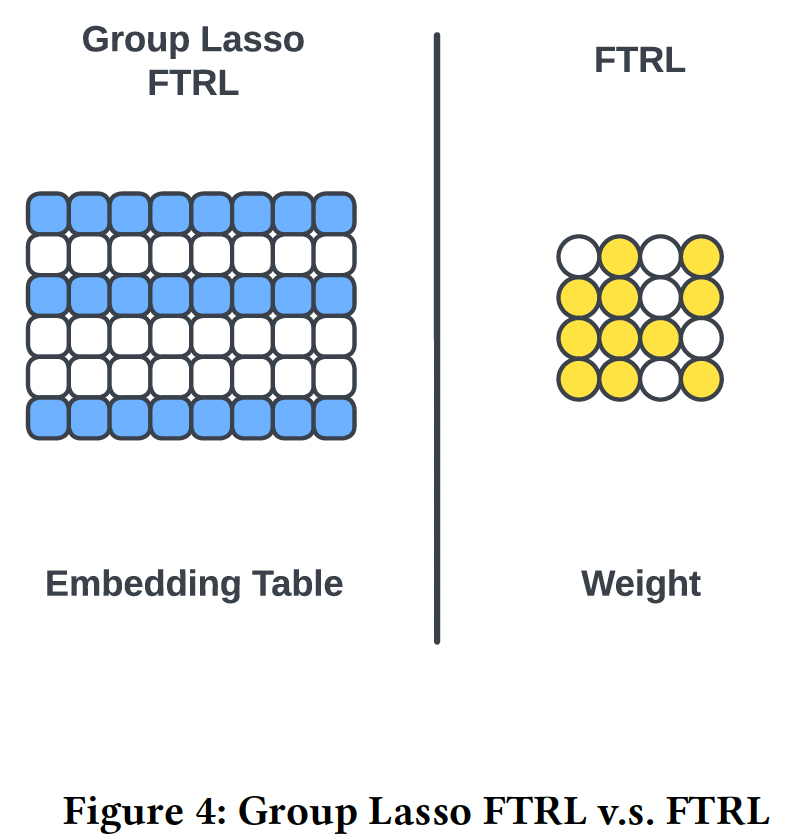
训练:我们使用
logloss作为损失函数:其中:
ground-truth,PIN和DCN之间的差异:PIN和DCN都采用了iterative的形式,然而它们在网络架构上有所差异。对
DCN而言,第其中:
对于
DCN,feature map被展平并拼接成单个向量。所有高阶的bit-wise交互首先通过这种结构导致了输出的特殊格式。如
《xdeepfm: Combining explicit and implicit feature interactions for recommender systems》所述,DCN层的输出是xdeepfm的论文也指出了DCN的缺点:DCN的输出是一种特殊的形式,每个隐层的输出都是- 交互只以
bit-wise的方式出现。
PIN用Hadamard product建模vector-wise特征交互,保留了vector-wise level信息。为了让不同的
field在vector level上交叉,PIN首先通过线性变换iterative PIN layer聚合input feature map,并通过PIN保持了vector-wise特征交互,并且不限制输出为此外,每个
PIN层都与输入feature mapPIN的多项式逼近的属性。
xDeepInt分析:考虑具有PIN层、以及subspace crossing机制的xDeepInt模型。subspace crossing机制采用field,embedding size为多项式逼近:参考原始论文。
作者仅仅只是把
PIN的公式进行展开,然后说明这是多项式逼近。并未从理论上证明。时间复杂度:
- 第
PIN层计算feature mapfeature map的计算总成本是 - 额外的成本还有
Hadamard product和残差连接。对于
在实践中,
field数量embedding size对于一个
DNN,每层都有bit-wise交互时,xDeepInt的时间复杂度比DNN高。- 第
空间复杂度:
embedding layer包含field的cardinality。- 输出层需要聚合最后一个
PIN layer的feature map。因此,输出层需要 subspace crossing机制在每个PIN layer需要
xDeepInt的总体空间复杂度大约为embedding sizeDNN,每层有为了降低
xDeepInt的空间复杂度,我们可以应用xDeepFM中介绍的方法:通过利用矩阵分解,用两个低秩矩阵取代权重矩阵
37.2 实验
数据集:
Avazu, Criteo, iPinnYou。对于
Criteo数据集,根据Criteo竞赛冠军的做法,我们将所有数值特征离散化为整数,离散化函数为:根据
AutoInt论文的做法,应该是:对于
iPinYou,我们遵循《Real-time bidding benchmarking with ipinyou dataset》的数据处理步骤。对于所有的数据集,我们随机地拆分为三个部分:
70%用于训练、10%用于验证、20%用于测试。我们还删除了每个categorical feature中出现少于20次的低频特征。
注意,我们想比较自动学习高阶特征交互的效果和效率,所以我们不做任何特征工程,只做特征变换,如数值特征分桶、以及
categorical特征的频次阈值。评估指标:
LogLoss, AUC。baseline方法:logistic regression: LR、factorization machine: FM、DNN(普通的多层感知机)、Wide & Deep、DeepCrossing、Deep & Cross Network: DCN、PNN(同时包含内积层和外积层)、DeepFM、xDeepFM、AutoInt、FiBiNET。配置:我们使用
Tensorflow实现所有的模型。mini-batch size设为4096。所有特征的embedding size设为16。关于优化器,对于神经网络模型我们采用学习率为
0.001的Adam优化器,对于LR和FM我们采用学习率为0.01的FTRL。关于正则化,我们选择了
L2正则化,稠密层的正则化为在验证数据集上对每个
baseline模型的超参数进行了网格搜索:DNN, Cross, CIN, Interacting layers的搜索空间为[1, 2, 3, 4]。- 神经元的搜索数量从
128到1024。
所有的模型都是带早停的训练,每
2000个训练步进行评估。对于
xDeepInt的超参数搜索:feature interaction layer的搜索空间为[1, 2, 3, 4]。- 子空间数量
[1, 2, 4, 8, 16]。由于我们的embedding size是16,这个范围覆盖了从完全的vector-wise交互到完全的bit-wise交互。
我们对
embedding table使用G-FTRL优化器、对PIN层使用FTRL优化器,学习率为0.01。
性能比较如下表所示:
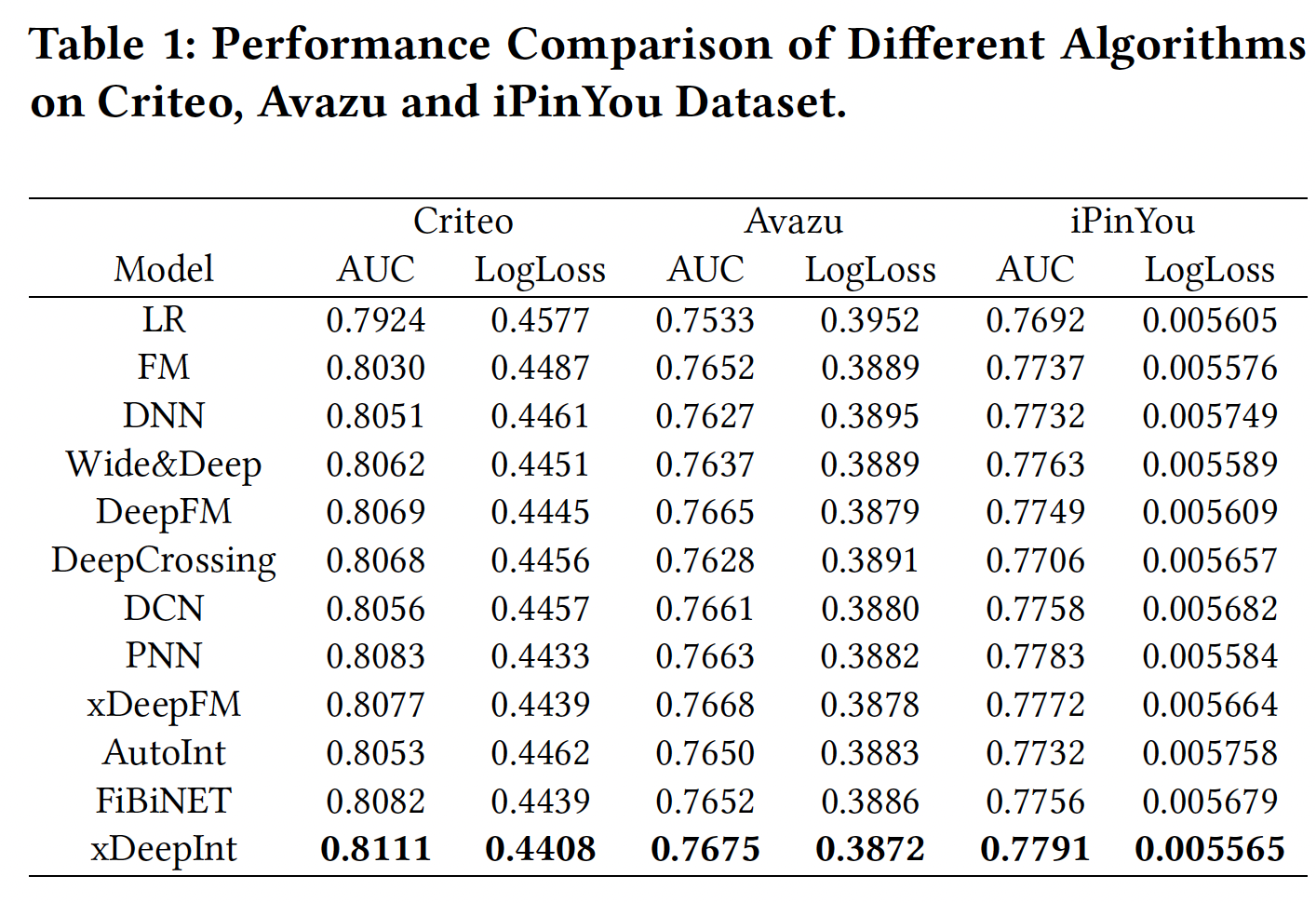
超参数研究:
网络深度:当层数为
0时,我们的模型等价于LR,没有学习任何交互。可以看到当层数在3 ~ 4时,模型效果最佳。这里我们将子空间的数量设置为bit-wise特征交互。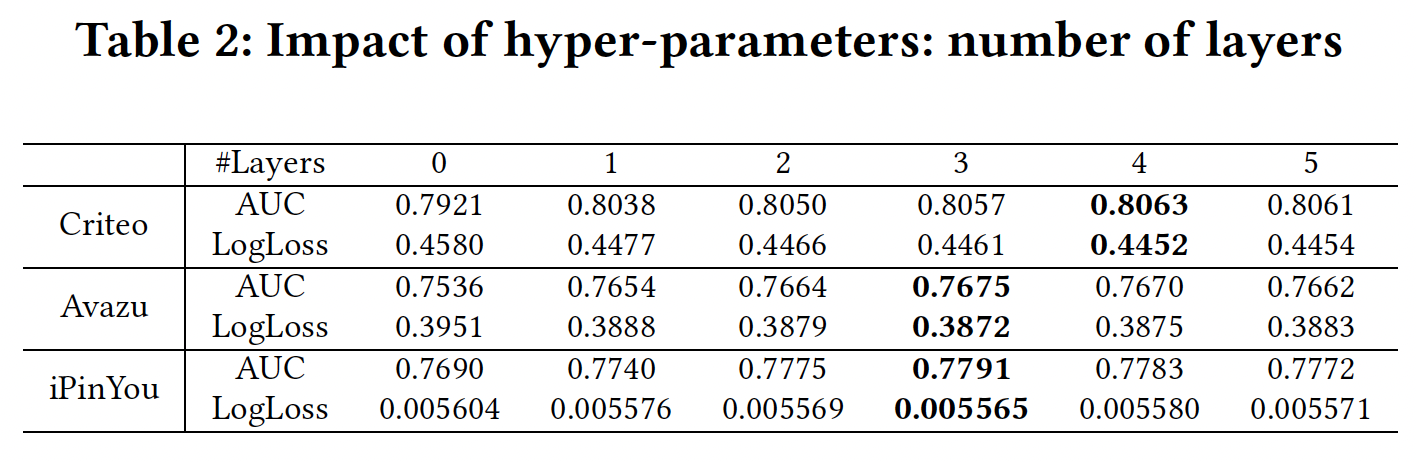
子空间数量:
subspace-crossing机制改善了性能。这里我们将PIN层的数量设为3,这通常是一个很好的选择,但不是每个数据集的最佳设置。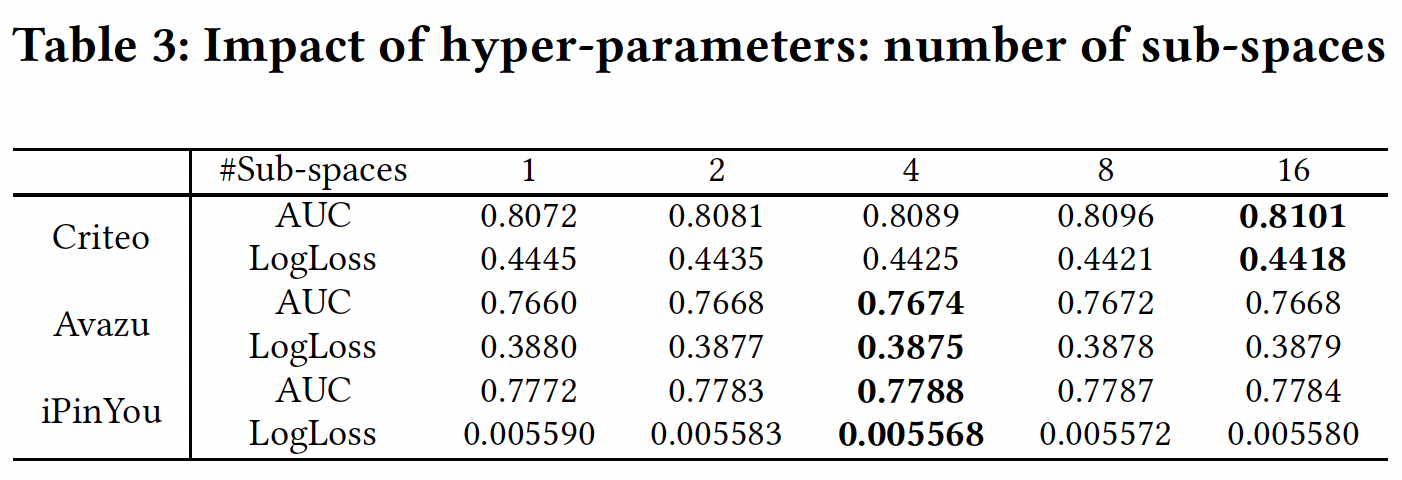
激活函数:线性激活函数对
PIN来说是最有效的。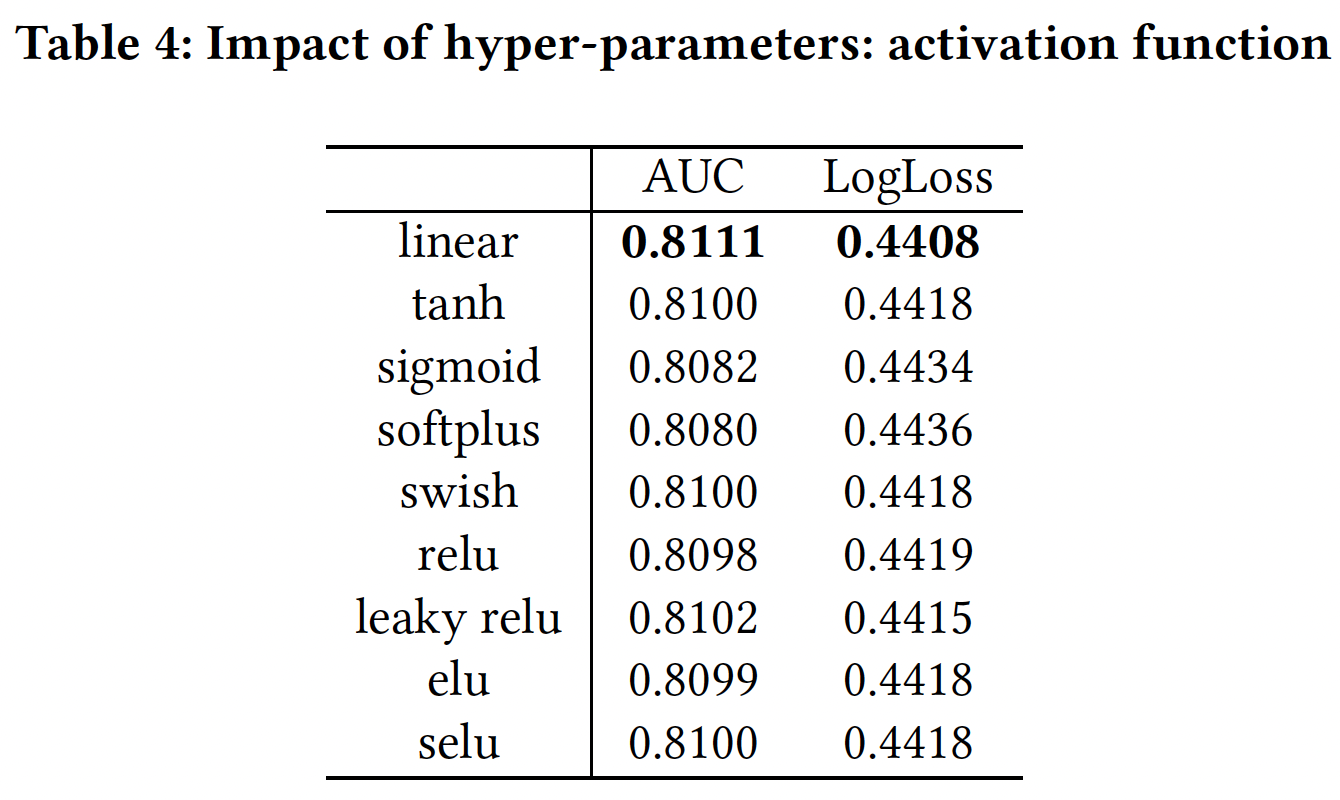
优化器:
G-FTRL and FTRL组合优化策略取得了更好的性能。并且我们的优化策略得到了更高程度的特征稀疏率(embedding table中所有zero embedding vector的占比)和特征交互稀疏率(PIN层中零权重的占比),这导致了轻量级模型。有一点需要注意的是:当使用
Adam优化器时,xDeepInt仍然在所有模型中取得了最好的预测性能,这表明了xDeepInt架构的有效性。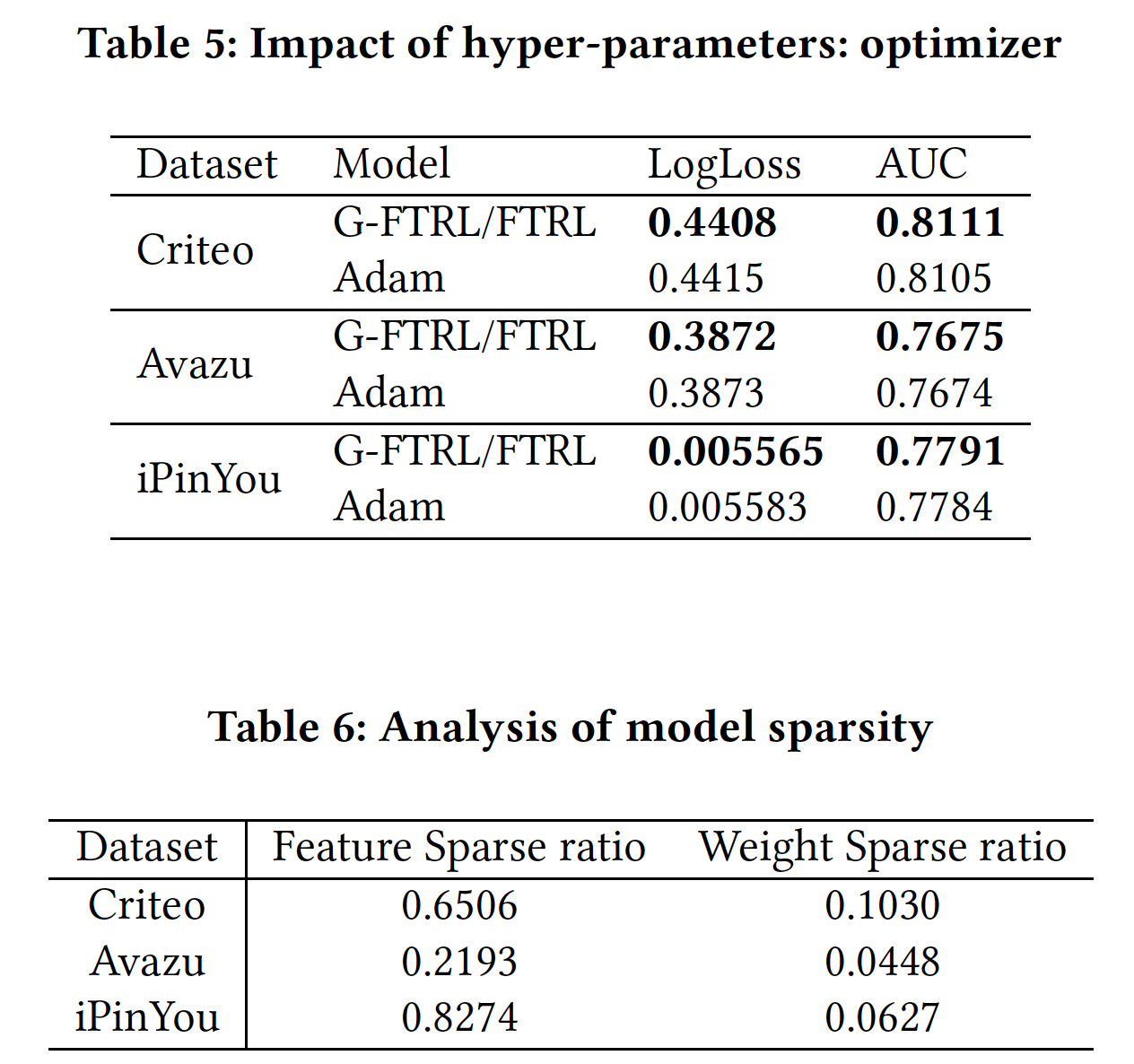
集成隐式交互:这里我们进行了消融研究,比较了我们提出的模型在集成隐式特征交互、以及不集成隐式特征交互的情况下的性能。在本实验中,我们将
xDeepInt与三层前馈神经网络联合训练,并将组合模型命名为xDeepInt+,与普通xDeepInt进行比较。可以看到:联合训练的前馈神经网络并没有提高普通
xDeepInt的性能。原因是普通xDeepInt模型已经通过subspace-crossing机制学习了bit-wise交互。因此,前馈神经网络并没有带来额外的预测能力。这里的联合训练,指的是结构并行(而不是堆叠式)。
三十八、BarsCTR[2021]
与其他数据类型(如图像和文本)相比,
CTR预测问题通常涉及大规模和高度稀疏的数据,并包括许多不同field的categorical feature(例如,在Google Play的app推荐中,有数十亿的样本和数百万的特征)。因此,在CTR预测中大幅提高准确性是一个巨大的挑战。CTR预测的重要性和独特的挑战已经吸引了学术界和工业界的大量研究关注。CTR预测模型已经从简单的logistic regression : LR、factorization machine: FM和决策树,发展到deep neural network: DNN。值得注意的是,许多深度模型已经被提出,并在工业的CTR预测问题上显示出显著的性能提升,如Wide&Deep、DeepFM、DCN、xDeepFM、FiBi-NET、DIN,等等。尽管这些研究取得了成功,但仍然缺乏标准化的
benchmark和统一的CTR预测任务的评估协议。因此,即使采用了一些常见的数据集(如Criteo和Avazu),现有的研究往往会进行他们自己的数据集拆分(例如,使用未知的train-test拆分,或使用未知的随机数种子)、以及预处理步骤(关于如何处理数值特征,以及如何过滤低频的categorical feature)。这导致了这些研究中的实验结果不可复现,甚至不一致,因为他们的非标准化的数据预处理使得任何两篇不同的论文的结果都没有可比性。每项工作都声称在他们自己的data partition上取得了显著改进的最佳结果,然而没有人知道:如果采用相同的评估协议进行公平的比较会是什么结果。由于缺乏公开的benchmarking结果作为参考,读者可能会怀疑论文中的baseline模型是否实现正确、是否经过了严格的超参数调优,但是这些研究都没有报告细节、也没有公开他们baseline实现的源代码。在某些case中,一些流行模型的官方或第三方源代码是可用的(如DeepCTR),但我们发现关于超参数设置、数据加载、以及early stopping的训练细节通常是缺失的,这使得我们很难重用代码来复现已有结果。 这种不可复现性和不一致性问题在很大程度上限制了该领域研究的实用价值和潜在影响。此外,由于文献中缺乏可重复使用和可比较的
benchmarking结果,研究人员在发表新的论文时,需要重新实现所有的baseline,并在自己的data partition上重新评估。这是一项繁琐而冗余的工作,严重地增加了研究人员开发新模型的负担。受
ImageNet benchmark在CV领域、以及GLUE benchmark在NLP领域的成功启发,在论文《BarsCTR: Open Benchmarking for Click-Through Rate Prediction》中,作者建议对CTR预测进行open benchmarking。论文不仅规范了CTR预测的open benchmarking pipeline,而且还对不同的模型进行了严格的比较,以便进行可复现的研究。为此,论文用统一的setup在12000多个GPU hours内进行了7000多个实验,在两个广泛使用的数据集(包括Criteo和Avazu)的多个数据集setting上重新评估了24个现有模型。论文的实验显示了有些令人惊讶的结果:经过充分的超参数搜索和模型调优,许多模型的差异比预期的要小,有时甚至与文献中的报道不一致。一项类似的研究(
《Are wereally making much progress? A worrying analysis of recent neural recommendation approaches》)也对推荐系统的多篇代表性论文进行了重新评估,提出了结果的可复现性问题以及对用于比较的baseline缺乏足够优化的担忧。与这项工作相比,作者更进一步,建立了一个CTR预测的open benchmark,记做BarsCTR。目前,BarsCTR已成为BARS benchmark project的主要benchmarking任务之一。BARS benchmark project旨在为推荐系统研究建立一个标准化的open benchmarking pipeline,并通过开放最全面的benchmarking结果以及有据可查的复现步骤,从而推动该领域的可复现研究。作者相信,这样的benchmarking研究对多个不同的读者群体都有好处:- 研究人员:该
benchmark不仅可以帮助研究人员分析现有模型的优势和瓶颈,还可以让他们方便地衡量新模型的有效性。此外,论文的benchmark还展示了一些良好的实践,为未来的研究提供公平的比较。 - 从业人员:
benchmark代码和结果可以帮助工业的从业者评估新研究模型在他们自己问题中的适用性,并允许他们在自己的数据集上以较少的努力尝试新模型。 - 比赛选手:利用论文的源代码和超参数,比赛选手可以在相关比赛中轻松实现高性能的
baseline和ensemble。 - 初学者:对于这个领域的初学者,特别是学生,论文的
benchmarking code(https://openbenchmark.github.io/ctr-prediction/)和详细的复现步骤可以作为学习CTR预测的模型实现和模型调优技巧的指导手册。将论文的项目用于教育目的也是很有价值的。
总而言之,论文的主要贡献如下:
- 就作者所知,论文的工作为
CTR预测的open benchmarking迈出了第一步。 - 论文在网站上公开了所有的
benchmarking code、评估协议、超参数设置和实验结果,以促进CTR预测的可复现性研究。 - 论文的工作揭示了现有研究中的不可复现性
non-reproducibility和不一致性inconsistency问题,并呼吁在未来的CTR预测研究中保持模型评估的开放性和严谨性。
- 研究人员:该
相关工作:
CTR Prediction:在过去的十年中,CTR预测模型被广泛研究,并经历了从线性模型、到FM、再到基于深度学习的模型的几代演变。这些工作被总结为以下几类:Feature interaction learning:虽然简单的线性模型(如LR和FTRL)由于简单和高效而被广泛使用,但它们很难捕捉到非线性特征。《Practical Lessons from Predicting Clicks on Ads at Facebook》提出了GBDT+LR的方法,应用Gradient Boosting Decision Tree: GBDT来抽取有意义的feature conjunction。FM:FM是一个有效的模型,通过特征向量的内积来捕获pairwise feature interaction。由于它的成功,人们从不同方面提出了许多后续模型,如field awareness(FFM, FwFM)、特征交互的重要性(AFM, IFM)、基于外积的交互(HFM)、鲁棒性(RFM)、可解释性(SEFM)。然而,这些模型在实践中无法捕获高阶特征交互。DNN:最近,深度学习已经成为推荐系统中的一种流行技术,产生了大量用于CTR预测的深度模型,包括YoutubeDNN, Wide&Deep, PNN, DeepFM, DistillCTR等等。其中一些模型旨在显式地捕获不同阶次的特征交互(如,DCN, xDeepFM),另一些模型探索使用卷积网络(如CCPM, FGCNN)、递归网络(DSIN, DIEN)、或注意力网络(AutoInt, FiBiNET)来学习隐式的特征交互。Behaviour sequence modeling:用户的历史行为对预测下一个item的点击概率有很大影响。为了更好地捕获这种历史行为(如item购买序列),最近的一些研究提出了通过注意力机制、LSTM、GRU、以及memory network为CTR预测建立用户兴趣模型。典型的例子包括DIN, DIEN, DSIN, HPMN, DSTN。Multi-task learning:在许多推荐系统中,用户可能会有点击以外的各种行为,如浏览、收藏、添加到购物车、以及购买。为了提高CTR预测的性能,最好能利用其他类型的用户反馈来丰富CTR预测的监督信号。为了实现这一目标,一些工作提出了multi-task learning模型(如,ESMM, MMoE, PLE)来学习不同用户行为之间的task relationship。Multi-modal learning:如何利用item丰富的多模态信息(如文本、图像和视频)来增强CTR预测模型是一个重要的研究问题,需要更多的探索。一些先驱性的工作证明了将多模态内容特征纳入CTR预测的有效性。
Benchmarking and Reproducibility:open benchmarking对促进研究进展很有价值。例如,ImageNet和GLUE是两个著名的benchmark,分别对计算机视觉和自然语言处理的进展做出了很大贡献。在推荐系统中,一些数据集(如Criteo和Avazu)被广泛使用。然而,仍然缺乏标准化的评估协议,这导致了现有研究的不一致性和不可复现性问题。值得注意的是,同时进行的一项工作(
《Are We Evaluating Rigorously? Benchmarking Recommendation for Reproducible Evaluation and Fair Comparison》)也报告了一些经典推荐模型的benchmarking结果。然而,他们的工作未能提供详细的配置和超参数设置,以实现可复现性。在这项工作中,我们通过建立第一个用于CTR预测的open benchmark、以及发布20多个模型的benchmarking结果,向可复现性研究迈出了重要一步。更重要的是,我们提供了所有的中间工件artifact(如复现步骤、运行日志),以确保我们结果的可复现性。
38.1 CTR Prediction
Overview:一般而言,一个CTR预测模型由以下关键部分组成:Feature Embedding:CTR预测的输入样本一般包含三组特征,即user profile, item profile, context information,每组特征都包含一些feature field。每个field的特征可以是categorical的、numeric的、或multi-valued的(例如,一个item的多个tag)。由于大多数特征是非常稀疏的,在
one-hot encoding或multi-hot encoding后会导致高维的特征空间,所以通常会应用feature embedding来将这些特征映射成低维的稠密向量。有三种类型的feature embedding过程:Categorical:对于一个categorical feature fieldone-hot feature vectorembedding matrix,embedding维度。Numeric:对于数值特征字段feature embedding的选择:- 可以通过对数值特征进行分桶从而转换为离散特征,通过手动设计(例如,将
13~19岁归为青少年)、或通过在数值特征上训练决策树(如,GBDT)。 - 给定一个归一化的标量值
embedding设为fieldshared embedding vector。 - 与其将每个值进行分桶、或为每个数值
field分配一个向量,例如应用AutoDis这种numeric feature embedding方法,动态地将数值特征分桶,并从meta embedding matrix计算embedding。
- 可以通过对数值特征进行分桶从而转换为离散特征,通过手动设计(例如,将
Multi-valued:对于一个multi-valued fieldembedding为:one-hot encoded vector,embeddingsum池化。一个进一步的潜在改进是应用序列模型(如
DIN中的target attention、以及DIEN中的GRU)来聚合multi-valued行为序列特征。
Feature Interaction:对于CTR预测任务,特征之间的交互(又称feature conjunction)是提高分类性能的核心。在factorization machine: FM中,内积被证明是一种简单而有效的方法来捕获pairwise feature interaction。自
FM成功以来,大量的研究致力于以不同的方式捕捉特征之间的交互。典型的例子包括:PNN中的内积层和外积层、NFM中的Bi-interaction、DCN中的cross network、xDeepFM中的compressed interaction、FGCNN中的卷积、HFM中的循环卷积、FiBiNET中的双线性交互、AutoInt的自注意力、FiGNN的图神经网络、InterHAt的分层注意力。此外,目前的大部分工作都在研究如何同时将显式特征交互和隐式特征交互(通过普通的全连接网络,即
MLP)结合起来。损失函数:二元交叉熵损失目前广泛应用于
CTR预测任务中,它的定义为:其中:
ground-truth,我们定义:
sigmoid函数,model function。
代表性的模型:
浅层模型:
Logistic Regression: LR:LR是CTR预测的一个简单的baseline模型。Factorization Machine: FM:FM将特征嵌入到稠密的向量中,并建模pairwise特征交互为相应embedding vector的内积。值得注意的是,FM是特征数量的线性时间复杂度。Field-aware factorization machine: FFM:FFM是FM的一个扩展,针对特征交互时考虑了field信息。 它是Kaggle关于CTR预测的几个竞赛中的获胜模型。HOFM:由于FM只能捕获到二阶的特征交互,HOFM旨在将FM扩展到高阶factorization machine。然而,它导致指数级的特征组合、消耗巨大的内存、并且需要很长的运行时间。FwFM:FwFM通过考虑特征交互的field-wise权重扩展了FM。与FFM相比,它的性能相当,但使用的模型参数少得多。LorentzFM:LorentzFM将特征嵌入双曲空间,并通过洛伦兹距离Lorentz distance的三角形不等式建模特征交互。
深层模型:与浅层模型相比,深层模型在捕获复杂的高阶特征交互方面更加强大,通常会产生更好的性能。然而,效率已经成为深层模型在实践中
scale的主要瓶颈。DNN:DNN是《Deep Neural Networks for YouTube Recommendations》报告的一个直接的深层模型,它在拼接feature embedding后应用一个全连接网络(称为DNN)进行CTR预测。CCPM:CCPM报告了使用卷积方法进行CTR预测的首次尝试,其中feature embedding通过卷积网络进行分层聚合。Wide&Deep:Wide&Deep结合了wide network(或浅层网络)和deep network,从而同时实现了两者的优势。IPNN:IPNN是product-based network,它将feature embedding的内积(或外积)作为DNN的输入。由于pairwise外积需要巨大的内存,我们选择内积版本,即IPNN。DeepCross:受残差网络的启发,《Deep Crossing: Web-Scale Modeling without Manually Crafted Combinatorial Feature》提出了deep crossing来在DNN层间增加残差连接。NFM:与PNN类似,NFM提出了一个Bi-interaction层,将pairwise特征交互池化为一个向量,然后将其馈入DNN进行CTR预测。AFM:AFM通过注意力网络学习特征交互的权重,而不是像FM那样平等对待所有的特征交互。与FwFM不同的是,AFM根据输入的数据样本动态地调整权重。DeepFM:DeepFM是Wide&Deep的一个扩展,它用FM代替LR,显式地建模二阶的特征交互。DCN:DCN提出了一个cross network,以显式的方式执行高阶的特征交互。此外,遵从Wide&Deep,它还集成了一个DNN网络。xDeepFM:DCN所建模的高阶特征交互是bit-wise的,但xDeepFM提出compressed interaction network: CIN以vector-wise的方式捕获高阶特征交互。HFM+:HFM提出了holographic representation,并通过循环卷积计算压缩外积来建模pairwise特征交互。HFM+进一步将DNN网络与HFM相结合。FGCNN:FGCNN应用卷积网络和recombination layer来生成额外的组合特征,以丰富现有的feature representation。AutoInt+:AutoInt利用自注意力网络来学习高阶的特征交互。AutoInt+将AutoInt与一个DNN网络整合在一起。FiGNN:FiGNN利用图神经网络的消息传递机制来学习高阶的特征交互。ONN(也叫NFFM):ONN是一个建立在FFM上的模型。它将FFM的交互输出馈入DNN网络。FiBiNET:FiBiNET利用squeeze-excitation network来捕获重要的特征,并提出bilinear interaction来加强特征交互。AFN+:AFN应用对数转换层logarithmic transformation layer来学习自适应阶次的特征交互。AFN+进一步将AFN与DNN网络整合在一起。InterHAt:InterHAt采用分层注意力网络,以有效的方式建模高阶特征交互。
38.2 实验
38.2.1 可复现性要求
我们强调了以下五个关键要求,以确保可复现的研究。然而,目前许多研究未能满足所有这些可复现性要求,如下表所示。请注意,我们用
✓ , - , ×分别表示每个要求是否完全、部分、或未满足。它还表示artifacts是否完全可用、部分可用或不可用从而复现每个step。例如,-表示FiBiNET只有非官方的模型源代码。- 数据预处理:大多数工作将训练集、验证集和测试集随机拆分,但其他人往往由于缺乏脚本、或使用的随机数种子而无法复现相同的数据拆分。更有甚者,一些预处理的细节(例如,如何处理数值特征、用什么阈值来过滤低频的
categorical feature)可能缺失或不完整。在这种情况下,研究人员不得不进行他们自己的数据拆分和预处理,从而导致无法比较的结果。值得注意的是,AutoIn、AFN和InterHAt的作者在分享数据处理代码或预处理数据方面做了一个很好的起点。 - 模型源代码:本着开源的精神,一些研究在
GitHub上发布了他们的模型源代码。一些流行的模型也有非官方的实现,可以从第三方库中获得(例如DeepCTR)。但在很多情况下,我们发现源代码还不能用于可复现性研究,因为它可能缺少训练代码(如加载数据、early stopping等)、或者错过了给定数据集上的一些关键超参数。 - 模型超参数:大多数研究在论文中指定了他们自己模型的详细超参数。但如果不能获得作者预处理的原始数据集,其他人在新的数据集拆分上使用相同的超参数是不合适的。它可能只能达到次优的性能,需要重新调参。这种做法会导致现有论文中出现不一致的结果。
baseline源代码:许多研究报告了他们自己模型的细节,但没有说明他们如何应用baseline模型。我们注意到,现有的研究很少开放baseline模型的源代码,也没有说明哪种实现被用于比较。模型的性能在很大程度上取决于其代码实现的质量。糟糕的实现可能会引入bias,并使模型的比较变得不公平。然而,这一方面往往被现有的研究所忽视,使得他们的性能改进难以复现。baseline超参数:最好能详尽地调优baseline模型的超参数以公平地比较模型的性能。然而,由于缺乏open benchmarking,这一点还没有得到保证。大多数现有的研究,由于其未知的数据预处理和baseline实现,通常报告同一baseline模型的不一致的结果。
为了实现研究的可复现性和比较的公平性,在这项工作中,我们旨在建立一个标准化的
benchmarking pipeline,并为CTR预测提供最全面的open benchmarking结果。
- 数据预处理:大多数工作将训练集、验证集和测试集随机拆分,但其他人往往由于缺乏脚本、或使用的随机数种子而无法复现相同的数据拆分。更有甚者,一些预处理的细节(例如,如何处理数值特征、用什么阈值来过滤低频的
38.2.2 评估协议
数据集:
Criteo和Avazu。我们之所以选择它们,是因为它们都是从生产中的真实点击日志中收集或采样的,而且都有数千万的样本,使得benchmarking结果对行业从业者有意义。下表总结了数据统计信息。我们还在BarsCTR网站上提供了更多数据集的benchmarking结果。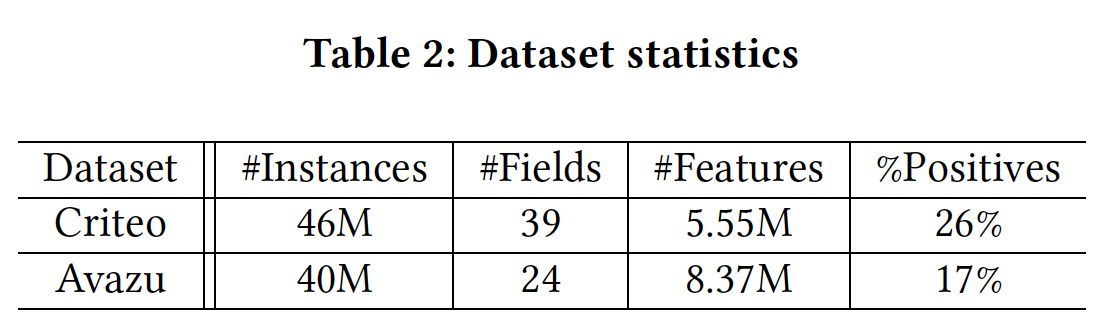
数据集拆分:遵循大多数现有的研究,分别将
Criteo和Avazu随机拆分为8:1:1从而作为训练集、验证集和测试集。为了使其完全可复现,并易于与现有工作进行比较,我们重用AutoInt提供的代码,并控制随机种子(即seed=2018)进行拆分。我们将这两个数据拆分分别记做Criteo_x4和Avazu_x4。数据预处理:我们主要遵循与
AutoInt相同的步骤对特征进行预处理。此外,我们做了一些修改,并修复了AutoInt中的一个缺陷,以改善benchmark结果。Criteo:我们创建了两个不同的评估设置,分别表示为Criteo_x4_001和Criteo_x4_002。Criteo_x4_001:对于数值特征,我们没有像
AutoInt那样对数值进行归一化处理,而是按照Criteo竞赛的获胜方案,将每个数值特征按照如下方式离散化从而获得更好的性能:对于数值特征:我们用默认的
"OOV" token取代低频特征(min_count=10)。
此外,我们还将
feature embedding的维度固定为16。Criteo_x4_002:与Criteo_x4_001不同之处在于,我们为categorical feature设置了min_count=2,而feature embedding维度在调优之后等于40。
Avazu:我们也创建了两个评估设置,即Avazu_x4_001和Avazu_x4_002。Avazu_x4_001:- 我们删除了在每个数据样本中具有
unique值的id字段,这对于CTR预测来说应该是无用的。但它在AutoInt中被保留了下来,导致了一个缺陷。 - 此外,我们将
timestamp字段转化为三个新字段:hour, weekday, is_weekend。 - 对于所有的
categorical feature,我们用默认的"OOV" token代替低频特征(min_count=2)。 - 我们进一步将
feature embedding的维度固定为16,正如AutoInt。
- 我们删除了在每个数据样本中具有
Avazu_x4_002:与Avazu_x4_001的不同之处在于,我们为categorical feature设置了min_count=1,而feature embedding维度在调优之后等于40。
我们强调,对于
Avazu_x4,我们设置了一个小的min_count阈值,因为它确实导致了比AutoInt中的原始设置(min_count=10)更好的性能。然而,我们注意到,在我们的benchmark中,不同模型之间的相对比较是公平的,因为所有的模型都处于相同的embedding size。我们的benchmark力求在进行模型比较时提高baseline的水平。评估指标:
AUC, logloss。Benchmarking toolkit:虽然有许多开源项目用于CTR预测,但它们大多以临时的方式实现一些模型,缺乏完整的workflow来进行benchmarking。具体而言,DeepCTR提供了一个很好的软件包,对许多CTR预测模型进行统一实现。尽管如此,我们的benchmarking需要一个完整的workflow(而不仅仅是CTR预测模型)。在这项工作中,我们建立了开源的
FuxiCTR toolkit(https://github.com/xue-pai/FuxiCTR) ,用于对CTR预测模型进行benchmarking,提供了关于可配置、可调优和可复现的惊人特性。FuxiCTR的代码由以下部分组成:- 数据预处理部分从
CSV文件中读取原始数据,转换所有数值特征、categorical feature、以及序列特征,并将转换后的数据输出到HDF5文件。 - 用
Pytorch以统一的方式实现了数十个模型。 - 训练部分的实现是为了读取
batch数据、计算前向传播和后向传播、并在必要时进行学习率衰减和early stopping。 seeding和logging工具也是专门为可复现性设计的,为每个benchmarking实验记录详细的运行日志(包括使用的超参数)。- 超参数调优部分提供了一个可配置的界面,允许对用户指定的超参数进行网格搜索。
我们将所有这些部分整合为一个完整的
benchmarking框架,使研究人员能够轻松地复用我们的代码,建立新的模型,或增加新的数据集。FuxiCTR的目标是为CTR预测的可复现性研究提供一个易于使用的软件包。- 数据预处理部分从
训练细节和超参数的调优:
- 在训练过程中,我们默认应用
Reduce-LR-on-Plateau scheduler,当给定指标停止改善时,将学习率降低10倍。 - 为了避免过拟合,当验证集上的指标在连续
2或3个epoch中停止改善时,就会采用early stopping。默认的学习率是 batch size最初被设置为10000,如果GPU出现OOM错误,则使用[5000, 2000, 1000]逐渐减少。 我们发现,对于在数百万样本上训练的CTR预测模型,使用大的batch size通常会使模型运行得更快,并达到更好的结果。- 考虑到大量的特征,
feature embedding通常占据了大部分的模型参数。为了公平起见,我们在两个独立的设置中分别将embedding固定为16或40。 - 我们还发现,正则化权重对模型性能有很大影响。因此,我们在
0 ~ 1的范围内仔细调优它,以10倍的搜索比例。 model size(如层数、隐层单元数)与数据高度相关,因此我们详尽地调优了这些超参数。- 我们还仔细调优了其他一些超参数(例如,是否使用
batch normalization),从而达到每个模型的最佳结果。 - 为了避免指数组合空间,我们通常先调优重要的超参数,然后再逐组调优其他参数。平均而言,我们对每个模型进行了
73次实验以获得最佳结果。所有的实验都是在一个共享的GPU集群上(P100 GPU)进行的,每个GPU有16GB内存。
- 在训练过程中,我们默认应用
可复现性:为了实现可重复性,我们保留了每个数据集拆分的
md5sum值。我们为每个实验明确设置随机数种子,并将数据设置和模型超参数记录到配置文件中。此外,我们选择在Pytorch中实现模型,因为它比Tensorflow有更好的能力来避免在GPU设备上运行模型时的非确定性。
38.2.3 结果分析
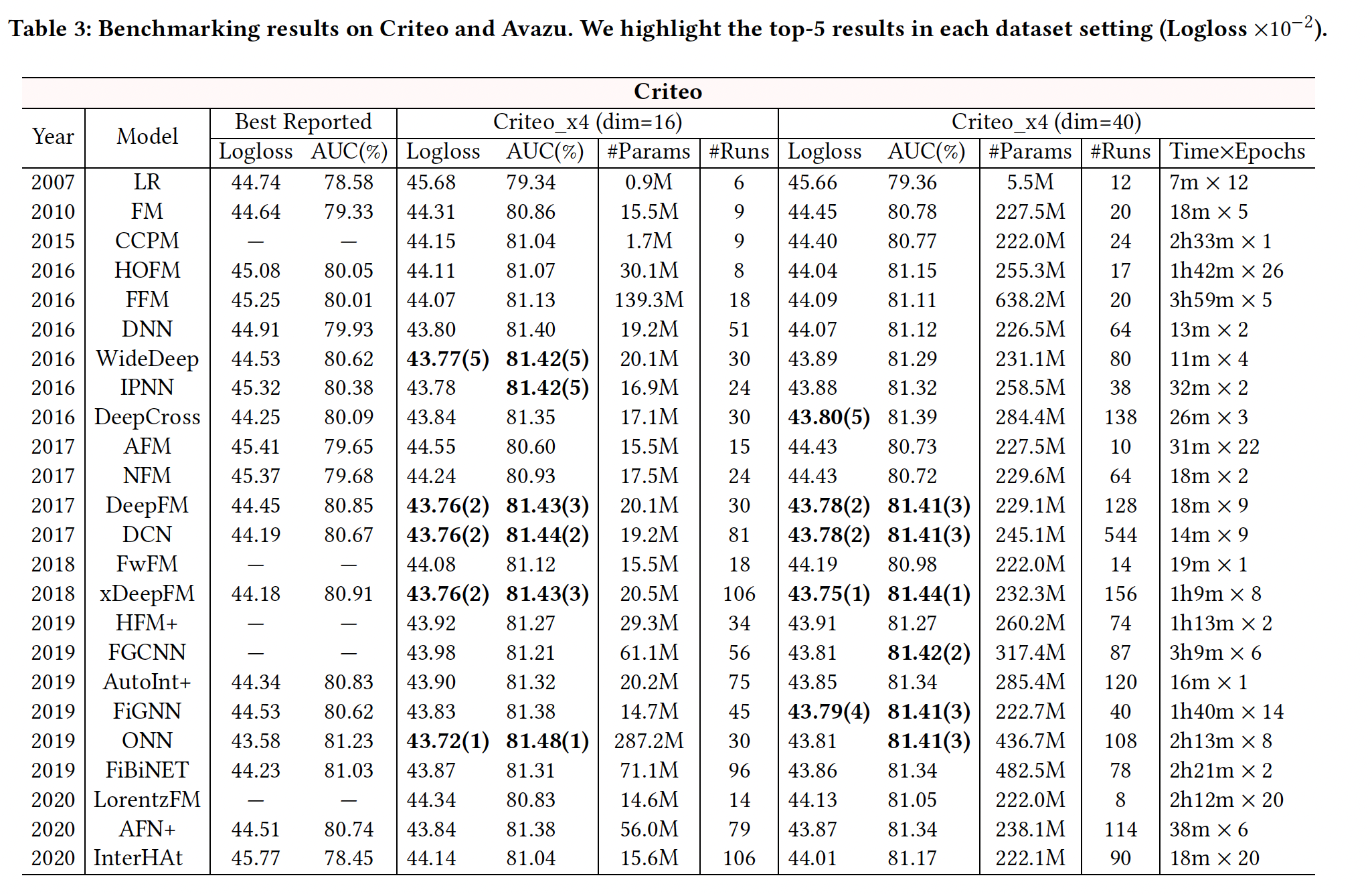
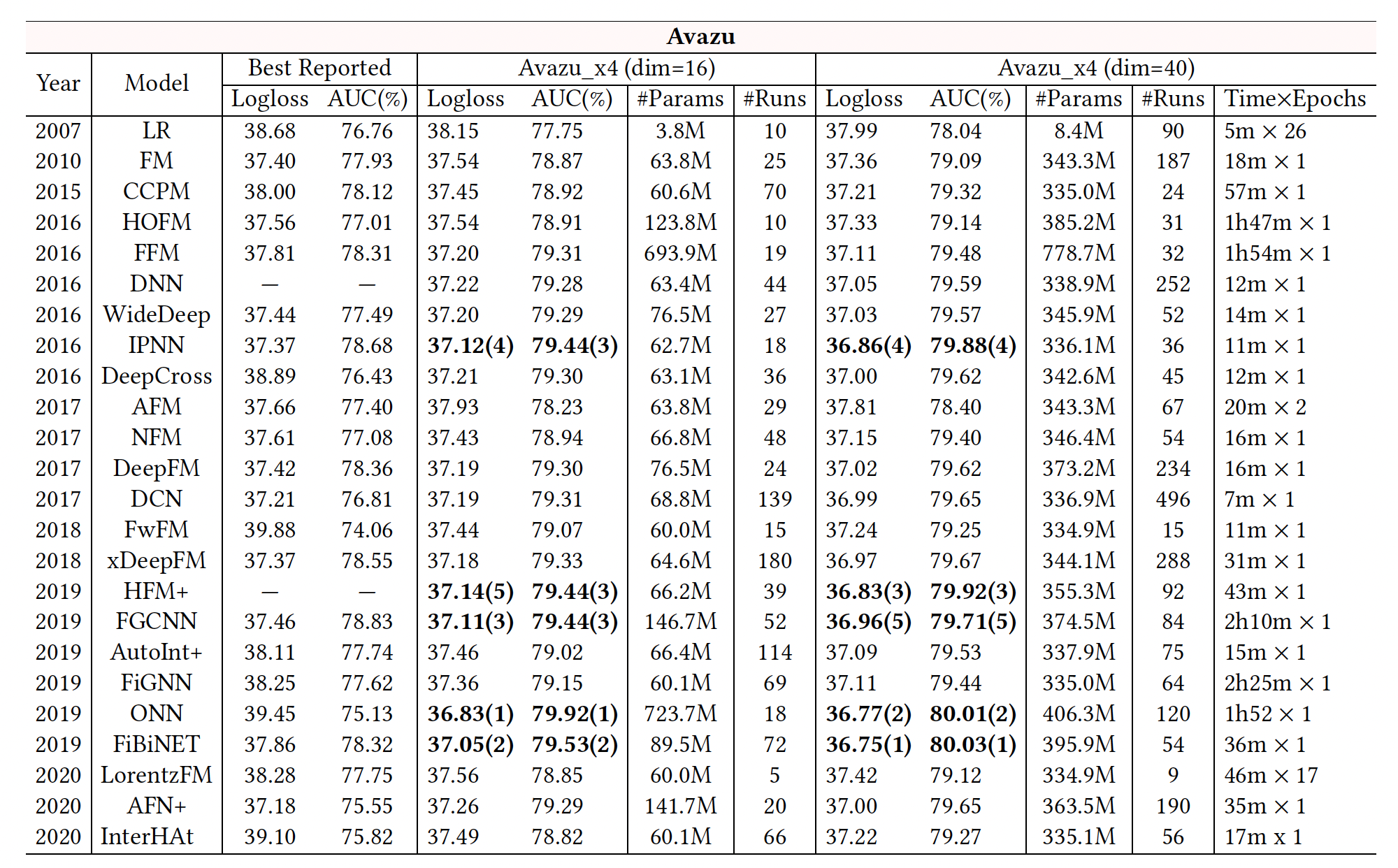
我们报告了
24个模型的benchmarking结果,如下表所示。"Best Reported"列显示了我们从现有研究中选出的关于Criteo和Avazu数据集的最佳结果。- 我们报告了我们在四个数据集(
Criteo _x4_001, Criteo_x4_002, Avazu_x4_001, Avazu_x4_002)setting上的benchmarking结果(logloss, AUC)。 - 对于模型的效率,我们也报告了
Criteo_x4_002和Avazu_x4_002的训练时间,即每个epoch的时间和epoch的数量。 - 此外,
"#Params"表示每个模型中使用的参数数量,"#Runs"记录了我们用网格搜索进行模型调优的实验次数。请注意,"#Runs"的数值通常取决于模型中要调优的超参数的数量。大量的运行(平均~73次)揭示了在我们的benchmarking中,模型已经得到了很好的调优。 - 此外,我们先在
Criteo_x4_002和Avazu_x4_002上运行实验,所以我们在Criteo_x4_001和Avazu_x4_001上进行了较少数量的实验来调优模型。
结论:
现有研究报告中的最佳结果显示出一定的不一致性。如:
InterHAt在两个数据集上的表现都比LR差;DeepCross在Avazu上的表现也比LR差。这主要是由于即使在相同的数据集上,通常也会采用不同的数据拆分或预处理步骤。这表明标准化的数据拆分和预处理是必要的,以使各模型之间的结果可以直接比较。
在我们的数据集
setting上进行模型调优后,我们大多获得了比最佳报告结果更好的性能。我们的
benchmarking遵循相同的评估协议,使结果具有可比性。然而,经过详尽的重新调优,我们发现
SOTA模型之间的差异变得很小。例如:IPNN, DeepFM, DCN, xDeepFM, ONN在Criteo上都达到了相同水平的准确性(∼0.814 AUC),而DNN, DeepFM, DCN, xDeepFM在Avazu上达到了可比的性能。此外,一些最新的模型(如
InterHAt, AFN+, LorentzFM)获得的结果甚至比先前的一些SOTA模型还要差。我们还在
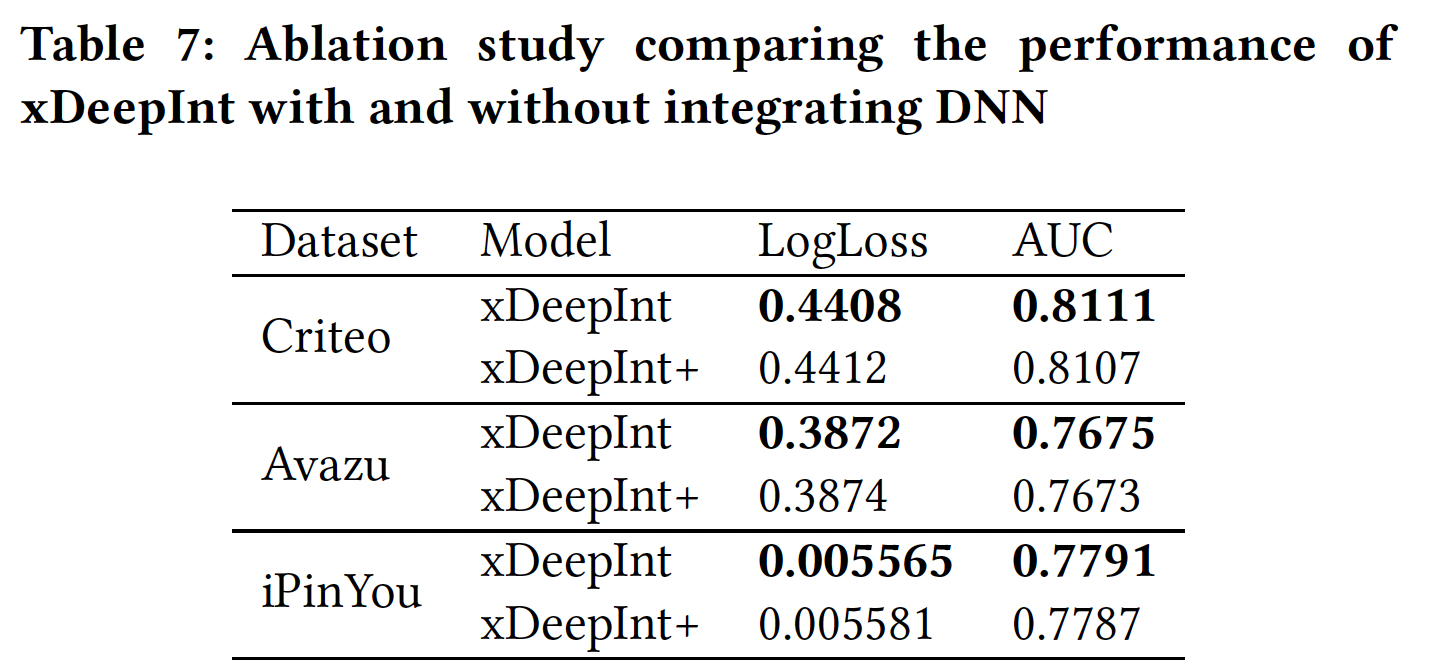
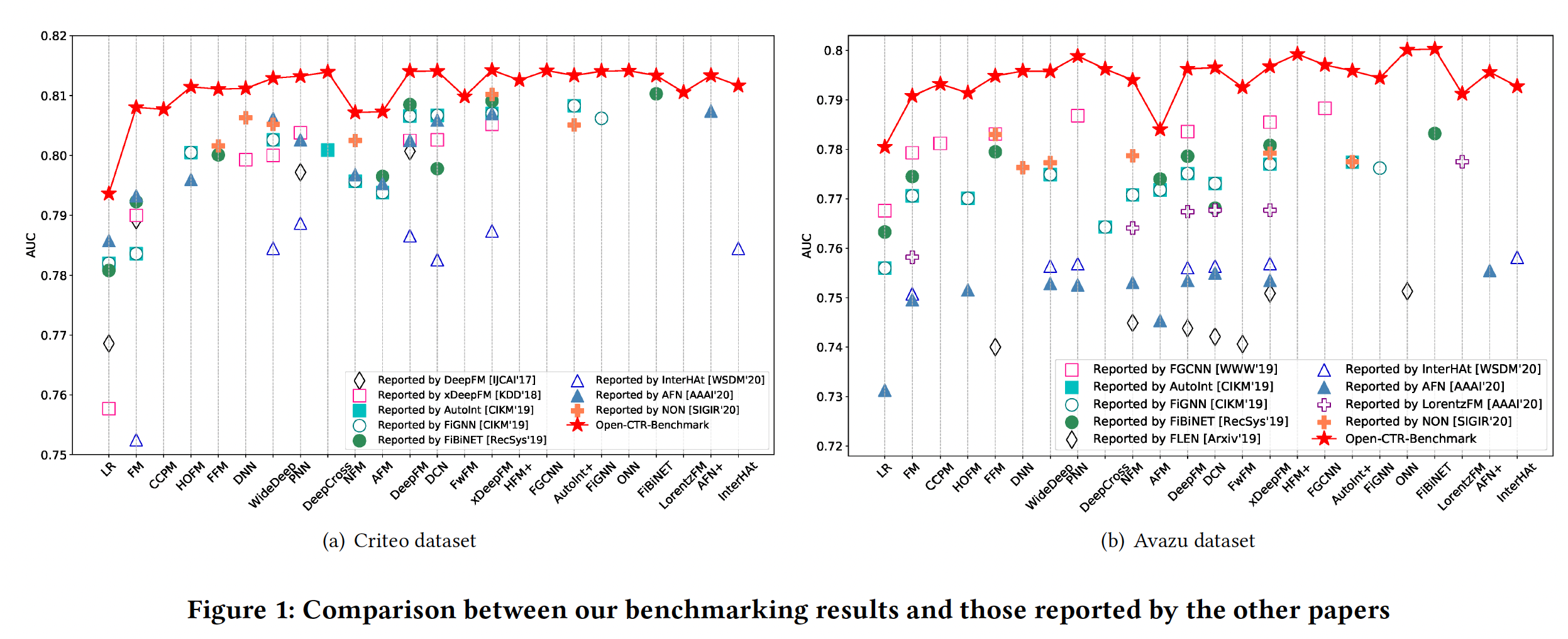
Figure 1中对我们的benchmarking结果和其他论文报告的结果进行了明确的比较。对于每个数据集,我们绘制了8∼9篇现有论文的AUC结果。我们可以看到,由于未知的数据拆分和预处理,不同论文的结果差异很大。一些最新的模型只获得了微弱的改进,有时甚至导致性能下降。值得注意的是,我们的
benchmarking提出了迄今为止所有模型的最佳结果。内存消耗和模型效率是工业
CTR预测任务的另两个重要方面。如下表所示,由于使用了卷积网络(如CCPM, FGCNN, HFM+)、field-wise交互(如FFM, ONN)、图神经网络(如FiGNN)等,一些模型运行非常缓慢(每个epoch数小时)。还有一些模型有更多的参数,如FFM, ONN, FGCNN等。这些缺点可能会阻碍它们在工业中的实际应用。整体而言,
IPNN, DCN的效果好、训练时间短,取得了良好的tradeoff。这两个模型都进行了显式的特征交叉,一个是堆叠式、一个是并行式。
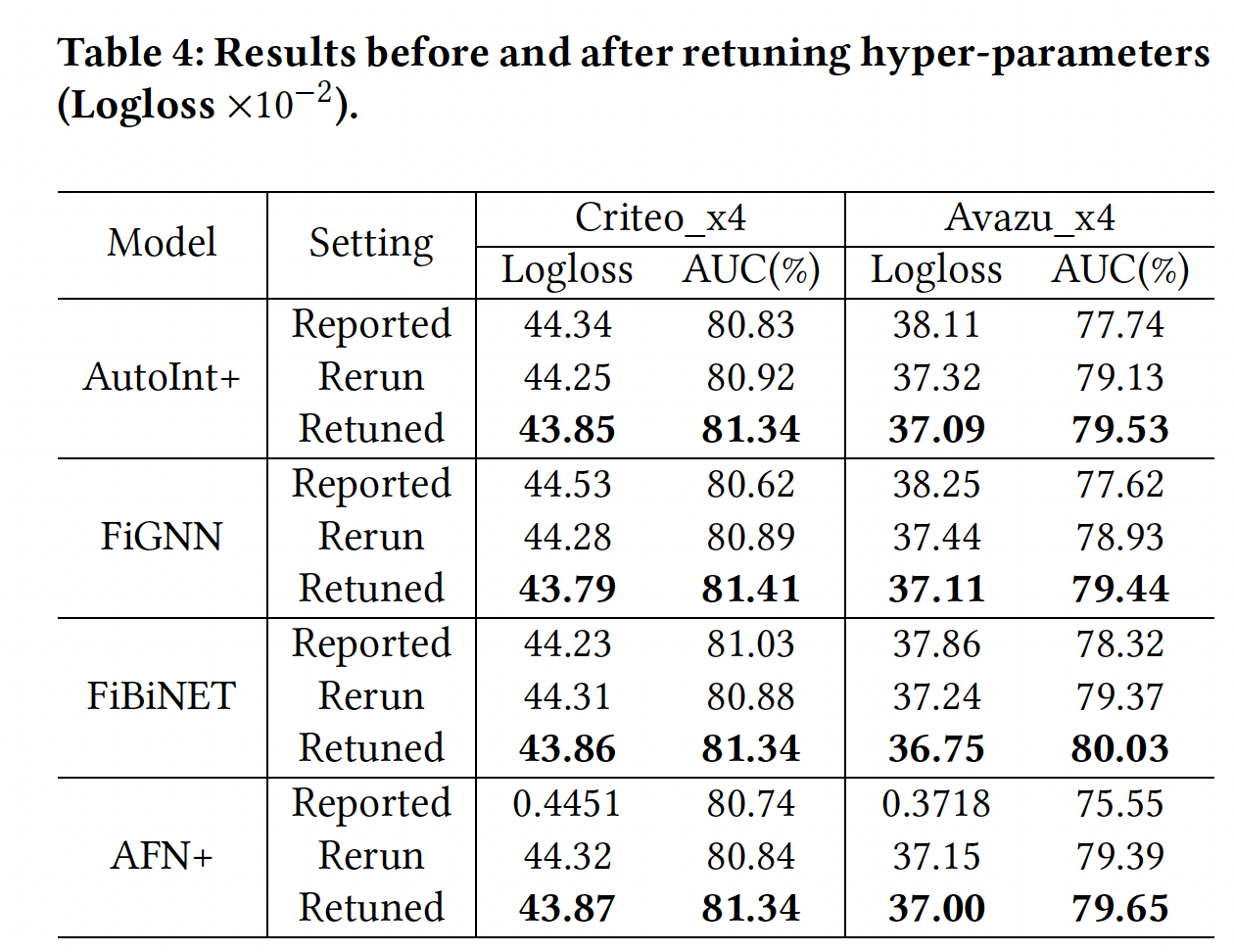
模型重新调优:为了进一步证明重新调优
baseline模型的必要性,在下表中,我们展示了四个代表性模型在三种setting下的结果:Reported setting:表示相应论文所报告的结果。Rerun setting:表示我们根据原始论文中给出的超参数,在我们的数据拆分上重新进行实验的情况。Retuned setting:表示广泛的超参数调优后取得的结果。
可以看到:
即使在相同的数据集上,直接复用原来的超参数来重新进行实验,也会在新的数据
setting中带来很大的性能gap(即我们case中的Criteo_x4_002和Avazu_x4_002)。在模型重新调优后,我们比原来的超参数取得了相当大的改进。这表明,在新的数据拆分上测试一个模型时,有必要重新调优超参数(即使是同一数据集)。
然而,我们不难发现,有些研究为了公平比较,选择遵循论文中使用的
baseline超参数,但他们在不同的数据拆分上进行实验。因此,希望有一个common benchmark来缓解这个问题。
38.2.4 性能调优的关键因素
在我们的
benchmarking工作中,我们也确定了一些对性能调优至关重要的关键因素:- 数据预处理:数据往往决定了一个模型的上限。然而,现有的工作很少在数据预处理期间对
categorical feature的min_counts阈值进行调优。在我们的工作中,我们为低频特征过滤设置了一个适当的阈值,这产生了更好的性能。 batch size:我们观察到,大的batch size通常会带来更快的训练和更好的性能。例如,如果GPU没有引发OOM错误,我们将其设置为10000。embedding size:虽然现有的工作在实验中通常将其设置为10或16,但我们也通过在GPU内存限制范围内使用更大的embedding size(如40)来实验其他setting。- 正则化权重和
dropout:正则化权重和dropout是减少模型过拟合的两个关键技术。它们对CTR预测模型的性能有很大影响。我们在一定范围内详尽地搜索最佳值。 batch normalization:在某些情况下,在DNN模型的隐层之间添加batch normalization可以进一步提升预测性能。
- 数据预处理:数据往往决定了一个模型的上限。然而,现有的工作很少在数据预处理期间对
局限性和未来方向:
- 更多数据集:
Criteo和Avazu这两个数据集都是匿名的,缺乏明确的user field和item field的信息。我们计划从工业规模的应用中扩展更多的数据集,使其成为一个更全面的用于CTR预测的open benchmark。 - 数据拆分:为了与大多数现有的研究保持一致,我们将数据集随机拆分。然而在生产中,如果
train - test分布有很大的不同,就有必要在预测后进行CTR校准。我们计划通过按时间顺序拆分数据来评估模型,并在必要时也进行CTR校准。 - 效率基准:在这个版本中,我们主要通过其训练时间来评估这些模型的效率。在将来考虑测试它们的推理时间。由于实时应用中的
CTR预测有严格的延迟限制。 - 超参数自动调优:如何为一个给定的模型快速找到最佳的超参数仍然是一个开放的研究问题。当数据随时间演变时,模型的超参数也需要重新调优以适应新的数据分布。我们非常期待探索一些先进的
AutoML技术从而以进一步促进未来的超参数调优过程。
- 更多数据集: