概率图模型
一、概率图模型
考虑三个随机变量 ,其联合概率分布为:
对每个随机变量引入一个节点,然后为每个节点关联上式右侧对应的条件概率。
对于每个条件概率分布,在图中添加一个链接(箭头):箭头的起点是条件概率的条件代表的结点。
对于因子 ,因为它不是条件概率,因此没有输入的链接。
如果存在一个从结点 到结点 的链接,则称结点 是结点 的父节点,结点 是结点 的子节点。
可以看到,上式的左侧关于随机变量 是对称的,但是右侧不是。
实际上通过对 的分解,隐式的选择了一个特定的顺序(即 )。如果选择一个不同的顺序,则得到一个不同的分解方式,因此也就得到一个不同的图的表现形式。
对于 个随机变量的联合概率分布,有:
它对应于一个具有 个结点的有向图。
- 每个结点对应于公式右侧的一个条件概率分布。
- 每个结点的输入链接包含了所有的编号低于它的结点。
这个有向图是全链接的,因为每对结点之间都存在一个链接。
实际应用中,真正有意义的信息是图中的链接的缺失,因为:
- 全链接的计算量太大。
- 链接的缺失代表了某些随机变量之间的不相关或者条件不相关。
设节点 的父节点集合为 ,则所有随机变量的联合概率分布为:
前面讨论的是:每个结点对应于一个变量。可以很容易的推广到每个结点代表一个变量的集合(或者关联到一个向量)的情形。
可以证明:如果上式右侧的每一个条件概率分布都是归一化的,则这个表示方法整体总是归一化的。
概率图模型
probabilistic graphical model就是一类用图来表达随机变量相关关系的概率模型:- 用一个结点表示一个或者一组随机变量。
- 结点之间的边表示变量间的概率相关关系。
概率图描述了:联合概率分布在所有随机变量上能够分解为一组因子的乘积的形式,而每个因子只依赖于随机变量的一个子集。
根据边的性质不同,概率图模型可以大致分为两类:
使用有向无环图表示随机变量间的依赖关系,称作有向图模型或者贝叶斯网络
Bayesian network。有向图对于表达随机变量之间的因果关系很有用。
使用无向图表示随机变量间的相关关系,称作无向图模型或者马尔可夫网络
Markov network。无向图对于表达随机变量之间的软限制比较有用。
概率图模型的优点:
- 提供了一个简单的方式将概率模型的结构可视化。
- 通过观察图形,可以更深刻的认识模型的性质,包括条件独立性。
- 高级模型的推断和学习过程中的复杂计算可以利用图计算来表达,图隐式的承载了背后的数学表达式。
二、贝叶斯网络
贝叶斯网络
Bayesian network借助于有向无环图来刻画特征之间的依赖关系,并使用条件概率表Conditional Probability Table:CPT来描述特征的联合概率分布。这里每个特征代表一个随机变量,特征的具体取值就是随机变量的采样值。
2.1 条件独立性
一个贝叶斯网 由结构 和参数 两部分组成,即 :
网络结构 是一个有向无环图,其中每个结点对应于一个特征。
若两个特征之间有直接依赖关系,则他们用一条边相连。
参数 定量描述特征间的这种依赖关系。设特征 在 中父节点的集合为 , 则 包含了该特征的条件概率表:
贝叶斯网结构有效地表达了特征间的条件独立性。
给定父节点集,贝叶斯网络假设每个特征与它的非后裔结点表达的特征是相互独立的。于是有:
推导过程:
贝叶斯网络中三个结点之间典型依赖关系如下图:
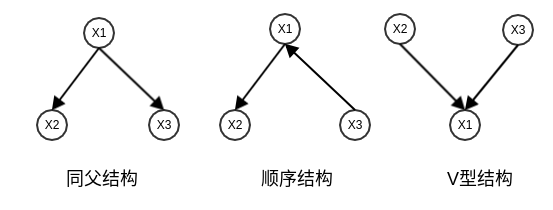
- 同父结构:给定父节点 的取值, 则 与 条件独立,即:
顺序结构:给定中间节点 的取值, 则 与 条件独立,即:
即:在 给定的条件下, 之间被阻断。因此它们关于 条件独立。
V型结构:给定子节点 的取值,则 与 必定不是条件独立的。即: 。事实上 与 是独立的(但不是条件独立的),即 。
- 同父结构:给定父节点 的取值, 则 与 条件独立,即:
为了分析有向图中节点之间的条件独立性,可以使用有向分离技术:
- 找出有向图中的所有
V型结构,在V型结构的两个父节点之间加上一条无向边。 - 将所有的有向边改成无向边。
这样产生的无向图称作道德图
moral graph。父节点相连的过程称作道德化moralization。基于道德图能直观、迅速的找到结点之间的条件独立性。- 找出有向图中的所有
2.2 网络的学习
贝叶斯网络的学习可以分为参数学习和结构学习两部分
参数学习比较简单。只需要通过对训练样本“计数”,估计出每个结点的条件概率表即可。
但是前提是必须知道网络结构。
结构学习比较复杂,结构学习被证明是
NP难问题。
贝叶斯网络的结构学习通常采用
评分搜索来求解。先定义一个评分函数,以此评估贝叶斯网络与训练数据的契合程度。然后基于这个评分函数寻找结构最优的贝叶斯网。
最常用的评分函数基于信息论准则:将结构学习问题视作一个数据压缩任务。
- 学习的目标是找到一个能以最短编码长度描述训练集数据集的模型。这就是
最小描述长度 Minimal Description Length:MDL准则。 - 此时的编码长度包括了:描述模型自身所需要的字节长度,和使用该模型描述数据所需要的字节长度。
- 学习的目标是找到一个能以最短编码长度描述训练集数据集的模型。这就是
给定训练集 ,贝叶斯网络 在 上的评分函数定义为:
其中: 表示描述每个参数 所需的字节数; 是贝叶斯网络的参数个数;
是贝叶斯网 的对数似然。因此:
- 第一项 是计算编码贝叶斯网络 所需要的字节数。
- 第二项 是计算 所对应的概率分布 需要多少字节来描述 。
现在结构学习任务转换为一个优化任务,即寻找一个贝叶斯网络 使评分函数 最小。
问题是,从所有可能的网络结构空间中搜索最优贝叶斯网络结构是个
NP难问题,难以快速求解。有两种方法可以在有限时间内求得近似解:
- 贪心算法。如从某个网络结构出发,每次调整一条边,直到评分函数不再降低为止。
- 增加约束。通过给网络结构增加约束来缩小搜索空间,如将网络结构限定为树形结构等。
贝叶斯网络训练好之后就能够用来进行未知样本的预测。
最理想的是直接根据贝叶斯网络定义的联合概率分布来精确计算后验概率,但问题是这样的“精确推断”已经被证明是
NP难的。此时需要借助“近似推断”,通过降低精度要求从而在有限时间内求得近似解,常用的近似推断为吉布斯采样(
Gibbs sampling)。
三、马尔可夫随机场
根据前面的介绍,有向图模型可以将一组变量上的联合概率分布分解为局部条件概率分布的乘积。无向图模型也可以表示一个分解形式。
马尔可夫随机场
Markov Random Field:MRF是一种著名的无向图模型。现实任务中,可能只知道两个变量之间存在相关关系,但是并不知道具体怎样相关,也就无法得到变量之间的依赖关系。
贝叶斯网络需要知道变量之间的依赖关系,从而对依赖关系(即条件概率)建模。
马尔科夫随机场并不需要知道变量之间的依赖关系。它通过变量之间的联合概率分布来直接描述变量之间的关系。
如: 两个变量的联合概率分布为:
1000 10 20 2000 则这个分布表示: 和 取值相同的概率很大。
事实上这里的 就是后面介绍的势函数。
- 它们的总和不一定为 1 。即:这个表格并未定义一个概率分布,它只是告诉我们某些配置具有更高的可能性。
- 它们并没有条件关系,它涉及到变量的联合分布的比例。
马尔可夫随机场可以应用于图像问题中。
- 每个像素都表示成一个节点,相邻像素之间相互影响。
- 像素之间并不存在因果关系,它们之间的作用是对称的。因此使用无向图概率模型,而不是有向图概率模型。
3.1 马尔科夫性
对结点 ,若去掉结点 之后 分属于两个联通分支,则称结点 关于结点 条件独立,记作 。
这一概念可以推广到集合。
分离集
separating set:如下图所示,若从结点集A中的结点到结点集B中的结点都必须经过结点集C中的结点,则称结点集A和结点集B被结点集C分离,C称作分离集。马尔可夫随机场有三个马尔可夫性定义:
- 全局马尔科夫性。
- 局部马尔科夫性。
- 成对马尔科夫性。
全局马尔可夫性
global Markov property:给定两个变量子集和它们的分离集,则这两个变量子集关于分离集条件独立。如上图,令结点集
A、B、C对应的变量集分别为 , 则 和 在给定 的条件下独立,记作: 。局部马尔可夫性
local Markov property:给定某变量的邻接变量,则该变量与其他变量(既不是该变量本身,也不是邻接变量)关于邻接变量条件独立。即:令 为图的结点集, 为结点 在图上的邻接结点, ,则有:
这是根据全局马尔可夫性推导而来
成对马尔可夫性
pairwise Markov property:给定两个非邻接变量,则这两个变量关于其他变量(即不是这两个变量的任何其他变量)条件独立。即:令 为图的结点集,令 为图的边集。对图中的两个结点 ,若 , 则有:
这也是根据全局马尔可夫性推导而来
3.2 极大团
考虑两个结点 ,如果它们之间不存在链接,则给定图中其他所有结点,那么这两个结点一定是条件独立的
因为这两个结点之间没有直接的路径,并且所有其他路径都通过了观测的结点。
该条件独立性表示为:
对于联合概率分布的分解,则一定要让 不能出现在同一个因子中,从而让属于这个图的所有可能的概率分布都满足条件独立性质。
这里引入团的概念:
对于图中结点的一个子集,如果其中任意两个结点之间都有边连接,则称该结点子集为一个团
clique。即:团中的结点集合是全连接的。若在一个团中加入团外的任何一个结点都不再形成团,则称该团为极大团
maximal clique。即:极大团就是不能被其他团所包含的团。
显然,每个结点至少出现在一个极大团中。
如下图所示
- 所有的团有:
- 极大团有:
可以将联合概率分布分解的因子定义为团中变量的函数,也称作势函数。
它是定义在随机变量子集上的非负实函数,主要用于定义概率分布函数。
在马尔可夫随机场中,多个变量之间的联合概率分布能够基于团分解为多个因子的乘积,每个因子仅和一个团相关。
对于 个随机变量 ,所有团构成的集合为 , 与团 对应的变量集合记作 ,则联合概率 定义为:
其中:
- 所有团构成了整个概率图(团包含了结点和连接), 任意两个团之间不互相包含(但是可以相交)。
- 为与团 对应的势函数,用于对 团 中的变量关系进行建模。
- 为规范化因子,确保 满足概率的定义。
- 实际应用中, 的精确计算非常困难。但是很多任务往往并不需要获得 的精确值。
在上述 计算公式中,团的数量会非常多。如:所有相互连接的两个结点都会构成一个团。这意味着有非常多的乘积项。
注意到:若团 不是极大团,则它必被一个极大团 所包含。此时有: 。
于是: 随机变量集合 内部随机变量之间的关系不仅体现在势函数 中,也体现在势函数 中(这是根据势函数的定义得到的结论)。
于是: 联合概率 可以基于极大团来定义。假定所有极大团构成的集合为 , 则有
Hammersley-Clifford定理:其中: 为规范化因子,确保 满足概率的定义 。
通常贝叶斯网络可以将因子定义成表格形态,而马尔可夫随机场将因子定义为势函数。因为马尔可夫随机场无法将因子表格化。
假设有 个随机变量 ,它们的取值都是 。假设马尔可夫随机场中它们是全连接的,则其联合概率分布需要 个参数。
如果表达成表格形态,横轴表示连接的一个端点、纵轴表示连接的另一个端点,则需要 个参数。当 较大的时候, ,因此表格无法完全描述马尔可夫随机场的参数。
全局马尔可夫性的一个证明:
将上图简化为如下所示:
最大团有两个: ,因此联合概率为:
基于条件概率的定义有:
根据:
将 和 代入,有:
考虑 :
- 同理,可以推导出:
于是有:
有向图和无向图模型都将复杂的联合分布分解为多个因子的乘积:
无向图模型的因子是势函数,需要全局归一化。
优点是:势函数设计不受概率分布的约束,设计灵活。
有向图模型的因子是概率分布,不需要全局归一化。
优点是:训练相对高效。
3.3 势函数
势函数 的作用是刻画变量集 中变量之间的相关关系。
与有向图的联合分布的因子不同,无向图中的势函数没有一个具体的概率意义。
- 这可以使得势函数的选择具有更大的灵活性,但是也产生一个问题:对于具体任务来说,如何选择势函数。
- 可以这样理解:将势函数看做一种度量:它表示局部变量的哪种配置优于其他配置。
势函数必须是非负函数(确保概率非负),且在所偏好的变量取值上具有较大的函数值。 如:
- 该模型偏好变量 拥有相同的取值;偏好 拥有不同的取值。
- 如果想获取较高的联合概率,则可以令 和 相同,且 和 不同。
通常使用指数函数来定义势函数:
其中 是一个定义在变量集 上的实值函数,称作能量函数。
指数分布被称作玻尔兹曼分布。
联合概率分布被定义为势函数的乘积,因此总能量可以通过将每个最大团中的能量相加得到。
这就是采取指数函数的原因,指数将势函数的乘积转换为能量函数的相加。
常见形式为:
其中:
- 表示系数; 表示约束条件。
- 上式第一项考虑每一对结点之间的关系;第二项考虑单个结点。
3.4 图像降噪应用
马尔可夫随机场的一个应用是图像降噪。
如下图所示,左侧图片为原始图像,右侧图片为添加了一定噪音(假设噪音比例不超过 10%) 的噪音图像。现在给定噪音图像,需要得到原始图像。
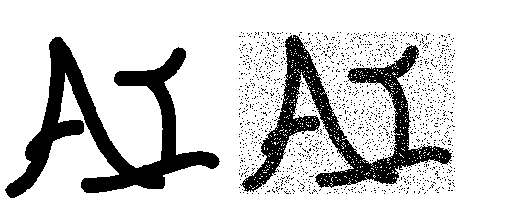
设随机变量 表示噪音图像中的像素,随机变量 表示原始图像中的像素。其中:
- 代表图片上的每个位置。
- 。当它们取
+1时,表示黑色;取-1时,表示白色。
由于已知噪音图像,因此 的分布是已知的。原始图像未知,则 的分布待求解。
由于噪音图像是从原始图像添加噪音而来,因此我们认为: 和 具有较强的关联。
由于原始图像中,每个像素和它周围的像素值比较接近,因此 与它相邻的像素也存在较强的关联。
因此我们假设: 只和它直接相邻的像素有联系(即:条件独立性质)。
因此得到一个具备局部马尔可夫性质的概率图模型。模型中具有两类团:
- 团 :原始图像的像素和噪音图像的像素。
- 团 :原始图像的像素和其直接相邻的像素。
这两类团就是模型中的最大团。
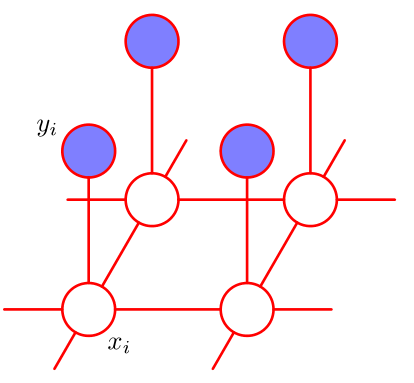
定义能量函数:
- 对于团 ,定义能量函数:。即: 相同时,能量较低; 不同时,能量较高。
- 对于团 ,定义能量函数:。即: 相同时,能量较低; 不同时,能量较高。
- 另外对于团 , 这个整体,定义能量函数: 。 即: 较大时,能量较高; 较小时,能量较低。
于是得到整体的能量函数为:
其中 为原始图像的相邻像素连接得到的边。
考虑到 ,根据最大似然准则,则模型优化目标是:
对于能量函数最小化这个最优化问题,由于每个位置的 都可以取2 个值 ,因此有 种取值策略, 为原始图像的像素数量。如果 较大,则参数的搜索空间非常巨大。
实际任务中通过
ICM算法、模拟退火算法、或者graph cuts算法来解决这个参数搜索问题。
四、条件随机场 CRF
生成式概率图模型是直接对联合分布进行建模,如隐马尔可夫模型和马尔可夫随机场都是生成式模型。
判别式概率图模型是对条件分布进行建模,如条件随机场
Conditional Random Field:CRF。条件随机场试图对多个随机变量(它们代表标记序列)在给定观测序列的值之后的条件概率进行建模:
令 为观测变量序列, 为对应的标记变量序列。条件随机场的目标是构建条件概率模型 。
即:已知观测变量序列的条件下,标记序列发生的概率。
标记随机变量序列 的成员之间可能具有某种结构:
- 在自然语言处理的词性标注任务中,观测数据为单词序列,标记为对应的词性序列(即动词、名词等词性的序列),标记序列具有线性的序列结构。
- 在自然语言处理的语法分析任务中,观测数据为单词序列,标记序列是语法树,标记序列具有树形结构。
令 表示与观测变量序列 和标记变量序列 对应的无向图, 表示与结点 对应的标记随机变量, 表示结点 的邻接结点集。若图 中结点对应的每个变量 都满足马尔可夫性,即:
则 构成了一个条件随机场。
4.1 链式条件随机场
理论上讲,图 可以具有任意结构,只要能表示标记变量之间的条件独立性关系即可。
但在现实应用中,尤其是对标记序列建模时,最常用的是链式结构,即链式条件随机场
chain-structured CRF。如果没有特殊说明,这里讨论是基于链式条件随机场。
给定观测变量序列 ,链式条件随机场主要包含两种关于标记变量的团:
- 单个标记变量与 构成的团: 。
- 相邻标记变量与 构成的团: 。
与马尔可夫随机场定义联合概率的方式类似,条件随机场使用势函数和团来定义条件概率 。
采用指数势函数,并引入特征函数
feature function,定义条件概率:其中:
:在已知观测序列情况下,两个相邻标记位置上的转移特征函数
transition feature function。- 它刻画了相邻标记变量之间的相关关系,以及观察序列 对它们的影响。
- 位置变量 也对势函数有影响。比如:已知观测序列情况下,相邻标记取值
(代词,动词)出现在序列头部可能性较高,而(动词,代词)出现在序列头部的可能性较低。
:在已知观察序列情况下,标记位置 上的状态特征函数
status feature function。- 它刻画了观测序列 对于标记变量的影响。
- 位置变量 也对势函数有影响。比如:已知观测序列情况下,标记取值
名词出现在序列头部可能性较高,而动词出现在序列头部的可能性较低。
为参数, 为规范化因子(它用于确保上式满足概率的定义)。
为转移特征函数的个数, 为状态特征函数的个数。
特征函数通常是实值函数,用来刻画数据的一些很可能成立或者预期成立的经验特性。
一个特征函数的例子(词性标注):
- 转移特征函数刻画的是:第 个观测值 为单词
"knock"时,相应的标记 和 很可能分别为[V]和[P]。 - 状态特征函数刻画的是: 第 个观测值 为单词
"knock"时,标记 很可能为[V]。
- 转移特征函数刻画的是:第 个观测值 为单词
条件随机场与马尔可夫随机场均使用团上的势函数定义概率,二者在形式上没有显著区别。
条件随机场处理的是条件概率,马尔可夫随机场处理的是联合概率。
的形式类似于逻辑回归。事实上,条件随机场是逻辑回归的序列化版本。
- 逻辑回归是用于分类问题的对数线性模型。
- 条件随机场是用于序列化标注的对数线性模型。
4.1.1 CRF 的简化形式
注意到条件随机场中的同一个特征函数在各个位置都有定义,因此可以对同一个特征在各个位置求和,将局部特征函数转化为一个全局特征函数。
这样就可以将条件随机场写成权值向量和特征向量的内积形式,即条件随机场的简化形式。
设有 个转移特征函数, 个状态特征函数。令 ,定义:
注意:要求 , 而 要求 ,因此对于边界条件要特殊处理。
对转移与状态函数在各个位置 求和,记作:
其中 为标记变量序列, 为观测变量序列。
该式子刻画的是特征函数在所有位置上的和,可以理解为特征函数在所有位置上的得的总分。
用 表示特征 的权值,即:
则条件随机场可以简化为:
其中 , 表示对所有可能的标记序列进行求和。
定义权值向量为 ,定义全局特征向量为:
则条件随机场可以简化为:
其中 , 表示对所有可能的标记序列进行求和。
的物理意义为:已知序列 的条件下,标记序列为 的未归一化的概率。它就是每个特征函数的总分的加权和(权重为特征函数的权重)。
4.1.2 CRF 的矩阵形式
假设标记变量 的取值集合为 , 其中 是标记的取值个数。
对于观测变量序列和标记变量序列的每个位置 ,定义一个 阶矩阵:
其中: 。i其中:
物理意义是:在位置 ,所有转移特征函数值加上所有状态特征函数值。对其取指数则是非规范化概率。
引入两个特殊的状态标记:起点状态标记 表示起始符,终点状态标记 表示终止符。
表示第 0 个位置的标记为 ,第 1个位置的标记为 。
第 0 个位置是一个虚拟符号,表示这是一个新的序列。因为 状态取值只能是 ,则:
表示第 个位置的标记为 ,第 个位置的标记为 。由于序列长度为 ,因此第 个位置是一个虚拟符号,表示该序列结束。因为 的取值只能是 ,则:
因此 和 中包含大量的 0 。
给定观测变量序列 , 标记变量序列 可以这样产生:
- 首先位于起点状态 。
- 然后从 转移到 。
- 最后到达终点状态 。
于是条件概率为:
其中 是以 为起点,以 为终点的所有标记路径的非规范化概率 之和 :
它也等于矩阵乘积 的结果的第一个元素(位于第一行第一列)的元素。
根据 和 的性质,该结果矩阵只有第一个元素非零,其他所有元素都为 0)。
如下图所示,上半部分是条件随机场的示意图,下半部分是条件随机场所有可能的路径。
- 除了起点和终点外,每个节点都有 个可能的取值。
- 起点取值只能是 , 终点取值只能是 。
- 红色粗实线给出了从起点到终点的一条可能的路径。
矩阵形式和前述形式是统一的:
与前述形式区别在于:这里由于引入了两个特殊的状态标记:起点状态标记、终点状态标记,从而累加的区间为 。
由于引入的状态标记是人为引入且状态固定的,因此相当于引入了常量。它会相应的改变 的值,最终结果是统一的。
4.2 概率计算问题
4.2.1 概率计算
条件随机场的概率计算问题是:已知条件随机场 ,其中 的取值集合为 , 给定观测值序列 , 给定标记值序列 ,其中 :
- 计算条件概率: 。
- 计算条件概率: 。
类似隐马尔可夫模型,可以通过前向-后向算法解决条件随机场的概率计算问题。
采用
CRF的矩阵形式,对于每个指标 ,(包括了起点标记和终点标记):定义前向概率 :表示在位置 的标记是 ,并且到位置 的前半部分标记序列的非规范化概率。
由于 的取值有 个,因此前向概率向量 是 维列向量:
定义后向概率 表示在位置 的标记是 ,并且从位置 的后半部分标记序列的非规范化概率。
由于 的取值有 个,因此后向概率向量 也是 维列向量:
根据
CRF的矩阵形式, 前向概率 的递推形式为:其物理意义是:所有从起点到 的路径再通过 转移到 。
根据前向概率向量 的定义,则也可以表示为:
根据
CRF的矩阵形式,后向概率 的递归形式为:其物理意义可以这样理解:从 到终点的路径可以这样分解:
- 先通过 从 到 。
- 再通过 到终点。
- 对所有可能的 累加,即得到从 到终点的路径。
根据后向概率向量 的定义,则也可以表示为:
根据前向-后向向量定义可以得到: 。其中:
- 为
CRF的矩阵形式中的归一化因子。 - 为元素均为 1 的 维列向量。
- 为
概率计算: 给定观测序列 ,给定标记值序列 ,其中 ,据前向-后向向量的定义,有:
- 标记序列在位置 处标记 的条件概率为:
标记序列在位置 处标记 ,且在位置 处标记 的条件概率为:
其中: 。
4.2.2 期望值计算
利用前向-后向向量可以计算特征函数 关于联合分布 和条件分布 的数学期望。
特征函数 关于条件分布 的数学期望为:
其中 。
如果合并所有的位置 ,则有特征函数 的期望为:
其物理意义为:在指定观测序列 的条件下,特征 的均值。
假设 的经验分布为 ,则特征函数 关于联合分布 的数学期望为:
如果合并所有的位置 ,则有特征函数 的期望为:
其物理意义为:在所有可能观测序列和标记序列中, 预期发生的次数。
上述两个式子是特征函数数学期望的一般计算公式。
- 对于转移特征函数 , 可以将上式中的 替换成 ,即得到转移特征函数的两个期望。
- 对于状态特征函数 ,可以将 替换成 ,即得到状态特征函数的两个期望。
4.3 CRF 的学习算法
条件随机场模型实际上是定义在时序数据上的对数线性模型,其学习方法包括:极大似然估计、正则化的极大似然估计。
具体的实现算法有:改进的迭代尺度法
Improved Iterative Scaling:IIS、 梯度下降法、拟牛顿法。给定训练数据集 ,其中:
代表第 个观测序列,其长度为 。
代表第 个观测序列的第 个位置的值。
代表第 个标记序列,其长度为 。
代表第 个标记序列的第 个位置的值,其中 。
同一组观测序列和标记序列的长度相同,不同组的观测序列之间的长度可以不同。
给定 个特征函数 ,其中:
而 为转移特征函数, 为状态特征函数。
条件随机场的学习问题是:给定训练数据集 和 个特征函数,估计条件随机场的模型参数。即模型中的参数 :
其中 为归一化参数。
注意到: 包含参数 ,同时 也受 影响,因此 将 记作 。因此将待求解的模型重新写作:
不受 的影响,因为 将变量 吸收掉。
考虑观测序列和标记序列 , 根据经验分布 , 该对序列出现的次数为 。
- 利用条件概率和经验分布 ,出现如此多次数的 概率为:
考虑整个训练集,则训练数据集 发生的概率为: 。
其对数似然函数为:
因为最终需要求解对数似然的最大值,考虑到 为常数,所以去掉该项,则有:
忽略约去常系数 ,则有: 。
与最大熵情况类似,这里使用了经验分布 ,但是并没有使用 来作为 的估计值,因为我们是针对该条件概率建模。
根据 的定义,有:
其形式和最大熵算法完全一致,因此可以直接使用最大熵算法的学习算法。
这也说明了,从最大熵原理可以推导出条件随机场的条件概率表示形式。
给定训练数据集 ,则可以获取经验概率分布 和 ,从而可以通过极大化训练数据的对数似然函数 来求解模型。
4.3.1 改进的迭代尺度法
IIS算法通过迭代的方法不断优化对数似然函数增量的下界,达到极大化对数似然函数的目的。具体推导可以参看最大熵算法。假设模型的当前参数向量是 , 参数向量的增量为 。更新的参数向量为 。
IIS推导的结果为:每一轮迭代中, 满足:将 放到 右侧,重新整理为:
其中:
- :为所有特征函数在序列 的所有位置的总和。
- :为特征函数 在训练集 中对所有序列样本的所有位置上的求和。
CRF学习的改进迭代尺度算法IIS:输入:
- 特征函数
- 经验分布
- 经验分布
输出:
- 参数估计值
- 模型
算法步骤:
初始化:对所有的 ,取值 。
迭代,迭代的停止条件是:所有 都收敛。迭代步骤为:
对每一个 ,从方程中计算出 :
更新 的值: 。如果不是所有 都收敛,继续迭代。
迭代终止时, 。
4.3.1.1 算法 S
在
IIS算法中, 为所有特征函数在序列 的所有位置的总和。对于不同的数据 , 很有可能不同。选择一个常数 ,定义松弛特征: 。
- 通常选择足够大的常数 ,使得对于训练数据集的所有数据 , 成立。
- 当每个特征函数的取值范围都是 时,则可以将 选取为: 。其物理意义为:所有潜在的特征函数取
1的位置的总数,乘以特征函数的数量。
将松弛特征代入,有:
考虑到 在 上恒成立,因此有:
因此对于下面两个方程的解:
必然有: 。
如果 ,则有:
因此可以将 作为 的一个近似。其物理意义为:更新 的值( )时,选择一个较小的更新幅度。
对于方程 ,其解为:
其中 。
CRF学习的算法S:输入:
- 特征函数
- 经验分布
- 经验分布
输出:
- 参数估计值
- 模型
算法步骤:
初始化:对所有的 ,取值 。
迭代,迭代的停止条件是:所有 都收敛。迭代步骤为:
对每一个 ,计算 :
其中 。
更新 的值: 。如果不是所有 都收敛,继续迭代。
迭代终止时, 。
4.3.1.2 算法 T
在算法
S中,通常需要使常数 取得足够大,此时每一步迭代的增量向量会较小,算法收敛会变慢。算法
T试图解决这个问题。算法
T对每个观测序列 ,计算其特征总数最大值 :记 ,由于 ,则对于下面两个方程的解:
必然有: ,原因与算法
S相同。因此可以将 作为 的一个近似。其物理意义为:更新 的值( )时,选择一个较小的更新幅度。
由于 ,因此算法
T求解的 会相对于算法S更大,使得算法收敛的更快。对于方程 ,有:
令: ,则有:
它就是一个以 为变量的非线性方程,求解该方程即可得到 的解。
CRF学习的算法T:输入:
- 特征函数
- 经验分布
- 经验分布
输出:
- 参数估计值
- 模型
算法步骤:
初始化:对所有的 ,取值 。
迭代,迭代的停止条件是:所有 都收敛。迭代步骤为:
对每一个 ,从方程中计算出 :
更新 的值: 。如果不是所有 都收敛,继续迭代。
迭代终止时, 。
4.3.2 拟牛顿法
条件随机场的对数似然函数为:
其中: 。
学习的优化目标是最大化对数似然函数 。
令:
于是学习优化目标是最小化 。
计算梯度:
CRF学习的BFGS算法:输入:
- 特征函数
- 经验分布
- 目标函数
- 梯度
- 精度要求
输出:
- 最优参数值
- 最优模型
算法步骤:
选定初始点 ,取 为正定对阵矩阵,置
计算 :
若 ,停止计算,得到
若 :
由 求得
一维搜索:求出 :
置
计算 。 若 ,停止计算,得到
否则计算 :
其中:
置 ,继续迭代。
4.4 预测算法
给定条件随机场 以及输入序列(观测序列) 的情况下,求条件概率最大的输出序列(标记序列) ,其中 。
根据条件随机场的简化形式:
其中 。
于是:
考虑到 与 无关,于是:
于是:条件随机场的预测问题就成为求非规范化概率最大的最优路径问题。
其中:
其中就是非规范化概率。
定义局部特征向量:
其物理意义为:每个特征函数在 的条件下,在位置 处的取值组成的向量。
于是: 。
为了便于统一描述,这里引入了两个人工标记: 。它们具有唯一的、固定的取值(不是随机变量)。
维特比算法用动态规划来求解条件随机场的预测问题。它用动态规划求解概率最大路径(最优路径),这时一条路径对应着一个标记序列。
根据动态规划原理,最优路径具有这样的特性:如果最优路径在位置 通过结点 , 则这一路径从结点 到终点 的部分路径,对于从 到 的所有可能路径来说,也必须是最优的。
只需要从位置 开始,递推地计算从位置 1 到位置 且位置 的标记为 的各条部分路径的最大非规范化概率。
于是在位置 的最大非规范化概率即为最优路径的非规范化概率 ,最优路径的终结点 也同时得到。
之后为了找出最优路径的各个结点,从终结点 开始,由后向前逐步求得结点 ,得到最优路径 。
假设标记 的取值集合为 , 其中 是标记的取值个数。
- 首先求出位置
1的各个标记值的非规范化概率:
根据递推公式,求出到位置 的各个标记取值的非规范化概率的最大值,同时记录非规范化概率最大值的路径:
- 其中 为:到位置 、且标记取值为 的非规范化概率的最大值。
- 为:到位置 且标记取值为 的最优路径中,位置 处的标记的取值的编号。
到 时,这时求得非规范化概率的最大值,以及最优路径的终点:
根据最优路径得到: 。
最终得到最优路径: 。
- 首先求出位置
CRF预测的维特比算法:输入:
- 模型特征向量 ,其中标记 的取值集合为
- 权值向量
- 观测序列
输出: 最优路径
算法步骤:
- 初始化: 。
- 递推:对 :
- 终止:
- 回溯路径: 。
- 返回路径 : 。
4.5 词性标注任务
在词性标注任务中,给定单词序列 ,需要给出每个单词对应的词性 。如:
他们 吃 苹果对应的标注序列为代词 动词 名词。- 给定一个单词序列,可选的标注序列有很多种,需要从中挑选出一个最靠谱的作为标注结果。
- 标注序列是否靠谱,是通过利用特征函数来对序列打分来获得。序列的得分越高(意味着非规范化概率越大),则越靠谱。
CRF中的特征函数接受四个参数:- 单词序列 。
- 位置 ,表示序列 中第 个单词。
- 标记 ,表示第 个单词的标注词性。
- 标记 ,表示第 个单词的标注词性。
特征函数的输出值为 ,表示满足/不满足这个特征。
每个特征函数对应一个权重 。
- 若权重为正,则说明该特征贡献一个正的分数;如果权重为负,则说明该特征贡献一个负的分数。
- 权重越大,则说明该特征靠谱的可能性越大(对于正的权重),或者该特征不靠谱的程度越大(对于负的权重)。
- 该权重是模型的参数,从训练集中训练得到。
4.6 CRF 与 HMM 模型
设已知隐马尔科夫模型的参数,则给定观察序列 ,以及标记序列 ,其出现的概率为:
对于
HMM中的每一个转移概率 ,定义特征函数:定义其权重为: 。
对于
HMM中每一个发射概率 ,定义特征函数:定义其权重为: 。
则有:
其中 为人工引入的 结点。
因此 的物理意义为:所有特征函数在所有位置之和。将其归一化之后就得到了
CRF的公式。
从推导中可以看出:每一个
HMM模型都等价于某个CRF模型。CRF模型比HMM模型更强大。因为
CRF模型能定义数量更多、更丰富多样的特征函数,能使用任意形式的权重。HMM模型中当前的标注结果只依赖于当前的单词,以及前一个标注结果。HMM模型转换过来的形式中,权重是条件概率的对数,因此权重都是负的。
HMM是生成式模型,而CRF是判别式模型生成式模型对联合概率建模,可以生成样本。
生成式模型定义的是联合概率,必须列举所有观察序列的可能值。在很多场景下,这是很困难的。
判别式模型对条件概率建模,无法生成样本,只能判断分类。