一、Cluster-GCN [2019]

《Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks》

1. 图卷积网络（ graph convolutional network: GCN ）在解决许多 graph-based 的应用程序中变得越来越流行，包括半监督节点分类、链接预测、推荐系统。给定一个图，GCN 使用图卷积操作逐层获得 node embedding ：在每一层，节点的 embedding 是通过收集其邻居的 embedding 来获得的，然后是一层或几层的线性变换和非线性激活。然后将最后一层的 embedding 用于一些终端任务。

   由于 GCN 中的图卷积运算需要利用图中节点之间的交互来传播 embedding，因此 GCN 的训练非常困难。和其它神经网络不同，GCN 的损失函数中每个节点对应的损失不是相互独立的，而是依赖于大量其它节点，尤其是当GCN 的深度很深时。相比之下，其它神经网络的损失函数中，每个样本的损失是相互独立的。由于节点的依赖性，GCN 的训练非常缓慢并且需要大量的内存，因为反向传播阶段需要将图中所有的 embeding 存储到 GPU 内存中。

   为了说明研究可扩展的 GCN 训练算法的必要性，我们从以下三个因素来讨论现有算法的优缺点：内存需求、epoch 训练速度（每个 epoch 的训练时间）、epoch 收敛速度（每个 epoch 损失函数下降的值）。这三个因素对于评估训练算法至关重要。注意：内存需求直接限制了算法的可扩展性，epoch 训练速度和epoch 收敛速度一起决定了整个训练时间。

   令 $n$$n$ 为图的节点数量、$d$$d$ 为 embedding 维度、$L$$L$ 为 GCN 的深度。

   • full-batch 梯度下降：GCN 原始论文使用 full-batch 梯度下降来训练。为计算整个训练集损失的梯度，它需要存储所有中间 embedding (intermediate embedding)，从而导致 $O(ndL)$$O(ndL)$ 的内存需求，因此难以扩展到大型图。

     另外，尽管每个 epoch 训练时间高效（单个 epoch 训练时间很短），但是单个 epoch 的收敛速度很慢，因为每个 epoch 仅更新一次参数。

     整体而言，full-batch 梯度下降内存需求差、epoch 训练速度快、epoch 收敛速度慢。

   • mini-batch 随机梯度下降：GraphSAGE 使用了基于 mini-batch 的随机梯度下降来训练。由于每次迭代仅基于 mini-batch 梯度，因此它可以减少内存需求，并在每个 epoch 进行多次更新从而加快 epoch 收敛速度。

     但是，由于邻域扩展问题，mini-batch 随机梯度下降会引入大量的计算开销：为计算第 $L$$L$ 层上单个节点的损失，它需要其邻域节点在第 $L-1$$L-1$ 层的 embedding，而这又需要邻域节点的邻域节点在第 $L-2$$L-2$ 层的 embedding，并向底层不断递归。这导致计算的时间复杂度和 GCN 的深度 $L$$L$ 呈指数关系。

     GraphSAGE 提出使用固定数量的邻域样本，而 FastGCN 提出了重要性采样。但是这些方法的开销仍然很大，并且当 GCN 层数更深时情况更糟。

     整体而言，mini-batch 随机梯度下降内存需求好、epoch 训练速度慢、epoch 收敛速度快。

   • VR-GCN：VR-GCN 提出方差缩减（variance reduction）技术来减少邻域采样规模。尽管这种方法成功地降低了邻域采样的数量（在Cluster-GCN 的实验中，VR-GCN 对每个节点仅采样 2 个邻居的效果很好），但是它仍然需要将所有节点的中间 embedding 存储在内存中，从而导致 $O(ndL)$$O(ndL)$ 的内存需求。如果图的节点规模达到数百万，则 VR-GCN 的内存需求可能太高导致无法放入到 GPU 中。

     整体而言，VR-GCN 内存需求差、epoch 训练速度快、epoch 收敛速度快。

   论文 《Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks》 提出了一种新的 GCN 训练算法，该算法利用图聚类结构 （graph clustering structure ）来加速GCN 的训练。

   作者发现：mini-batch 算法的效率可以通过 embedding 利用率（embedding utilization） 的概念来刻画。 embedding 利用率和单个 batch 内的边的数量成正比。这一发现促使作者利用图聚类算法来设计 batch，目标是构造分区（partition）使得同一个分区内的边的数量比跨区之间的边的数量更多。

   基于图聚类（graph clustering）的思想，作者提出了 Cluster-GCN：一种基于图聚类算法（如 METIS）来设计 batch 的算法。进一步地，作者提出一个随机多聚类框架 （stochastic multi-clustering framework）来改善 Cluster-GCN 的收敛性。

   核心思想是：尽可能地将内存和计算控制在 batch 内。这要求仔细安排 batch 内节点。

   但是，这么做破坏了 mini-batch 的随机性要求，因为 mini-batch 要求随机选取 $b$$b$ 个节点（$b$$b$ 为 batch-size），而 Cluster-GCN 中的采样方法不再随机。这使得 mini-batch 梯度不再是 full-batch 梯度的无偏估计。

   作者的解决办法是：随机将多个簇合并为一个大簇，然后将这个大簇作为 mini-batch ，使得 batch 内的节点分布尽可能和 full-batch 一致。

   Cluster-GCN 带来了巨大的内存优势和计算优势：

   • 在内存需求方面，Cluster-GCN 仅需要将当前 batch 中的节点 embedding 存储在内存中，内存复杂度为 $O(bdL)$$O(bdL)$ ，其中 $b$$b$ 为 batch-size 。这比 VR-GCN、full-batch 梯度下降、以及其它 mini-batch 随机梯度下降等方法要小得多。

   • 在计算复杂度方面，Cluster-GCN 在每个 epoch 都具有相同的时间代价，并且比邻域搜索方法快得多。

   • 在收敛速度方面，Cluster-GCN 相比其它 SGD-based 方法具有可比的竞争力。

   • 最后，Cluster-GCN 算法易于实现，因为它只需要计算矩阵乘法，而无需任何邻域采样策略。

   整体而言，Cluster-GCN 内存需求好、epoch 训练速度快、epoch 收敛速度快。

   通过对几个大型图数据集进行全面实验，证明了 Cluster-GCN 的效果：

   • Cluster-GCN 在大型图数据集（尤其是深层 GCN）上实现了最佳的内存使用效率。例如在 Amazon2M 数据集上的 3 层 GCN 模型中，Cluster-GCN 使用的内存比 VR-GCN 少 5 倍。

   • 对于浅层网络（例如 2 层），Cluster-GCN 达到了和 VR-GCN 相似的训练速度；但是当网络更深（如 4 层）时，Cluster-GCN 可以比 VR-GCN 更快。这是因为 Cluster-GCN 的复杂度和层数 $L$$L$ 呈线性关系，而 VR-GCN 的复杂度是 $L$$L$ 的指数级。

   • Cluster-GCN 能够训练具有很大 embedding size 并且非常深的网络。

     尽管之前的一些工作表明：深层 GCN 无法提供更好的性能，但是作者发现通过适当的优化，深层 GCN 可以帮助提高模型准确性。例如使用 5 层 GCN，Cluster-GCN 在 PPI 数据集上的accuracy 为 99.36，而之前的最佳效果为 98.71 。

1.1 模型

1. 给定图 $G=(\mathcal{V},\mathcal{E},\mathbf{A})$$G=(\mathcal V,\mathcal E,\mathbf A)$ ，其中：

   • $\mathcal{V}=\{v_1,\cdots ,v_n\}$$\mathcal V=\{v_1,\cdots,v_n\}$ 为节点集合，$n$$n$ 为节点数量。

   • $\mathcal{E}=\{e_{i,j}{\}}_{i,j}$$\mathcal E=\{e_{i,j}\}_{i,j}$ 为边的集合， $e_{i,j}$$e_{i,j}$ 表示节点 $v_i$$v_i$ 和 $v_j$$v_j$ 之间的边。

   • $\mathbf{A}\in {\mathbb{R}}^{n\times n}$$\mathbf A\in \mathbb R^{n\times n}$ 为邻接矩阵，如果节点 $v_i,v_j$$v_i,v_j$ 存在边则 $A_{i,j}=1$$A_{i,j} = 1$ 否则 $A_{i,j}=0$$A_{i,j} = 0$ 。

   • 节点 $v$$v$ 关联一个 $d_f$$d_f$ 维的特征向量 ${\overrightarrow{\mathbf{x}}}_v\in {\mathbb{R}}^{d_f}$$\mathbf{\vec x}_v\in \mathbb R^{d_f}$ 。 所有节点的特征向量按行拼接为特征矩阵 $\mathbf{X}\in {\mathbb{R}}^{n\times d_f}$$\mathbf X\in \mathbb R^{n\times d_f}$ ，第 $v$$v$ 行就是节点 $v$$v$ 的特征向量 ${\overrightarrow{\mathbf{x}}}_v$$\mathbf{\vec x}_v$ 。

   • 节点 $v$$v$ 关联一个label $y_v$$y_v$ ，所有带label 的节点集合为 ${\mathcal{V}}_Y$$\mathcal V_Y$ ，即观测节点集合。

   定义一个包含 $L$$L$ 层卷积层的 GCN，其中第 $l+1$$l+1$ 层卷积层为：

   $$\begin{array}{c}{\mathbf{Z}}^{(l+1)}=\mathbf{P}{\mathbf{H}}^{(l)}{\mathbf{W}}^{(l)}\\ {\mathbf{H}}^{(l+1)}=\sigma \left({\mathbf{Z}}^{(l+1)}\right)\end{array}$$

   其中：

   • ${\mathbf{H}}^{(l)}\in {\mathbb{R}}^{n\times d_l}$$\mathbf H^{(l)}\in \mathbb R^{n\times d_l}$ 为第 $l$$l$ 层的 representation 矩阵， $d_l$$d_l$ 为第 $l$$l$ 层 representation 向量的维度。${\mathbf{H}}^{(l)}$$\mathbf H^{(l)}$ 的第 $v$$v$ 行 ${\overrightarrow{\mathbf{h}}}_v^{(l)}$$\mathbf{\vec h}_v^{(l)}$ 表示节点 $v$$v$ 的第 $l$$l$ 层的 representation 向量。

     为简化讨论，我们假设 $d_f=d_1=\cdots =d_L=d$$d_f = d_1=\cdots=d_L = d$ 。

   • ${\mathbf{H}}^{(0)}=\mathbf{X}$$\mathbf H^{(0)} = \mathbf X$ 为输入的特征矩阵，第 $v$$v$ 行 ${\overrightarrow{\mathbf{x}}}_v$$\mathbf{\vec x}_v$ 表示节点 $v$$v$ 的特征向量。

   • $\mathbf{P}\in {\mathbb{R}}^{n\times n}$$\mathbf P\in \mathbb R^{n\times n}$ 为归一化的邻接矩阵：

     $$\begin{array}{c}\tilde{\mathbf{A}}=\mathbf{I}+\mathbf{A}\\ \tilde{\mathbf{D}}=\text{diag}({\tilde{D}}_i),{\tilde{D}}_i=\sum _j{\tilde{A}}_{i,j}\\ \mathbf{P}={\tilde{\mathbf{D}}}^{-1/2}\tilde{\mathbf{A}}{\tilde{\mathbf{D}}}^{-1/2}\end{array}$$

     其中 $\tilde{\mathbf{A}}$$\tilde{\mathbf A}$ 为添加了 self-loop 的邻接矩阵。

   • ${\mathbf{W}}^{(l)}\in {\mathbb{R}}^{d_l\times d_{l+1}}$$\mathbf W^{(l)}\in \mathbb R^{d_l\times d_{l+1}}$ 为第 $l+1$$l+1$ 层模型待学习的权重矩阵，它在所有节点上共享。

   • $\sigma (\cdot )$$\sigma(\cdot)$ 为非线性激活函数，通常为 ReLU 。

   GCN 模型的损失函数为：

   $$\mathcal{J}=\frac{1}{|{\mathcal{V}}_Y|}\sum _{v\in {\mathcal{V}}_Y}f(y_v,{\overrightarrow{\mathbf{z}}}_v^{(L)})$$

   其中：

   • $f(\cdot ,\cdot )$$f(\cdot,\cdot)$ 为单个节点的损失函数。

   • ${\overrightarrow{\mathbf{z}}}_v^{(L)}$$\mathbf{\vec z}_v^{(L)}$ 为 ${\mathbf{Z}}^{(L)}$$\mathbf Z^{(L)}$ 的第 $v$$v$ 行，表示节点 $v$$v$ 的 final representation。

2. 我们首先讨论之前方法的一些不足，从而启发我们提出 Cluster-GCN 。

   • 原始GCN：原始 GCN 中，作者通过 full-batch 梯度下降来训练 GCN，其计算代价和内存需求都很高。

     • 在内存需求方面，通过反向传播来计算损失函数的梯度需要 $O(ndL)$$O(ndL)$ 的空间来存储所有的 embedding 矩阵 ${\left\{{\mathbf{Z}}^{(l)}\right\}}_{l=1}^L$$\left\{\mathbf Z^{(l)}\right\}_{l=1}^L$ 。

     • 在收敛速度方面，由于模型每个 epoch 仅更新一次参数，因此模型需要训练很多个 epoch 才能收敛。

   • GraphSAGE：GraphSAGE 通过 mini-batch SGD 来改善 GCN 的训练速度和内存需求。SGD 不需要计算完整的梯度，而是仅在每轮更新中基于一个 mini-batch 来计算梯度。

     记 mini-batch 节点集合为 $\mathcal{B}\subset {\mathcal{V}}_Y$$\mathcal B\sub \mathcal V_Y$ ，令 $b=|\mathcal{B}|$$b=|\mathcal B|$ ，则每轮 SGD 迭代中，梯度的估计量为：

     $$\frac{1}{b}\sum _{v\in \mathcal{B}}\mathrm{\nabla }f(y_v,{\overrightarrow{\mathbf{z}}}_v^{(L)})$$

     尽管mini-batch SGD 在收敛速度方面更快，但是它在 GCN 训练过程中引入了另一种计算开销，这使得它与 full batch 梯度下降相比，每个 epoch 的训练速度慢得多。原因如下：考虑计算单个节点 $v$$v$ 的梯度 $\mathrm{\nabla }f(y_v,{\overrightarrow{\mathbf{z}}}_v^{(L)})$$\nabla f\left(y_v, \mathbf{\vec z}_v^{(L)}\right)$ ，显然这需要节点 $v$$v$ 的 embedding ${\overrightarrow{\mathbf{z}}}_v^{(L)}$$\mathbf{\vec z}_v^{(L)}$ ；而 ${\overrightarrow{\mathbf{z}}}_v^{(L)}$$\mathbf{\vec z}_v^{(L)}$依赖于节点 $v$$v$ 的邻域节点在第 $L-1$$L-1$ 层的 representation，而这又依赖于这些邻域节点的邻域节点在第 $L-2$$L-2$ 层的 representation ，... 。

     假设 GCN 具有 $L$$L$ 层并且每个节点的平均 degree 为 $D$$D$ ，则为了计算节点 $v$$v$ 的梯度，我们需要从 $O\left(D^L\right)$$O\left(D^L\right)$ 个其它节点中聚合特征。即：我们需要从节点 $v$$v$ 的 hop-k （$k=1,2,\cdots ,L$$k=1,2,\cdots,L$）邻域中抽取信息，从而计算节点 $v$$v$ 的梯度。由于聚合过程中涉及到和 ${\mathbf{W}}^{(l)}$$\mathbf W^{(l)}$ 的矩阵乘法，因此计算每层每个 representation 向量需要 $O(d^2)$$O(d^2)$ 的时间复杂度。因此计算单个节点梯度的平均时间复杂度为 $O(D^L{d}^2)$$O(D^Ld^2)$ 。

     如果一个 batch 中有很多节点，则时间复杂度就不是那么直接，因为不同节点具有重叠的 top-k 邻域，那么依赖的节点数量可以小于最差的 $O(b{D}^L)$$O(bD^L)$ 。

3. 为反应 mini-batch SGD 的计算效率，我们定义 embedding 利用率（ embedding utilization ） 的概念，从而刻画计算效率。

   在算法过程中，如果节点 $v$$v$ 在第 $l$$l$ 层的 embedding 计算之后，被第 $l+1$$l+1$ 层的 embedding 计算过程使用了 $u$$u$ 次，那么我们说 ${\overrightarrow{\mathbf{z}}}_v^{(l)}$$\mathbf{\vec z}_v^{(l)}$ 的 embedding 利用率为 $u$$u$ 。

   • 对于具有随机采样的 mini-batch SGD，由于图通常比较大且稀疏，因此 $u$$u$ 很小。假设 $u$$u$ 是一个很小的常数（即节点的 hop-k 邻域之间几乎没有重叠），则 mini-batch SGD 在每个 batch 需要计算 $O(b{D}^L)$$O(bD^L)$ 个 embedding，这导致每个 mini-batch 的训练时间为 $O(b{D}^L{d}^2)$$O(bD^L d^2)$ 、每个 epoch 的训练时间为 $O(n{D}^L{d}^2)$$O(nD^Ld^2)$ 。

   • 相反，对于 full-batch 梯度下降，每个 embedding 将在更上一层中重复利用 $D$$D$ 次（平均 degree），因此具有最大的 embedding 利用率。结果 full-batch SGD 在每个 epoch 需要计算 $O(nL)$$O(nL)$ 个 embedding，训练时间为 $O(nL{d}^2)$$O(nLd^2)$ 。这意味着仅需要计算 $O(L)$$O(L)$ 个 embedding 就可以得到一个节点的梯度，相比之下 mini-batch SGD 需要计算 $O(D^L)$$O(D^L)$ 个 embedding。

   如下图所示给出了传统的GCN 中指数级邻域扩展（左图）。红色节点是扩展的起始节点，不同颜色代表不同的 hop 。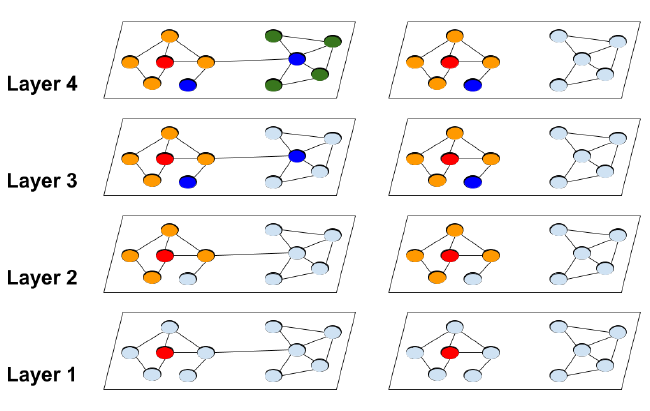

   

4. 为了使得 mini-batch SGD 顺利工作，已有的一些算法试图限制邻域扩展的大小，但是这无法提升 embedding 利用率。

   • GraphSAGE 均匀采样一个固定大小的邻域，而不是完整的邻域集合。我们将这个固定大小记作 $r$$r$ ，这将导致每个节点梯度需要计算 $O\left(r^L\right)$$O\left(r^L\right)$ 个 embedding，并且也使得梯度估计的准确性降低。

   • FastGCN 提出了一种重要性采样策略来改善梯度估计。

   • VR-GCN 提出了一种策略，通过存储所有 $n$$n$ 个节点在 $L$$L$ 层上所有 embedding 的历史均值，从而应用于未采样邻居节点的 embedding 计算。

     尽管存储所有 $nL$$nL$ 个 embedding 的内存需求很高，但我们发现该策略非常有效，并且在实践中即使对于非常小的 $r$$r$ （$r=2$$r=2$ ）也可以产生很好的收敛。

1.1.1 Cluster-GCN

1. Cluster-GCN 技术受到以下问题的启发：在 mini-batch SGD 更新过程中，能否设计 mini-batch 以及对应的计算子图，使得最大程度地提高 embedding 利用率？解决该问题的关键在于将 embedding 利用率和聚类相结合。

   考虑我们计算 batch $\mathcal{B}$$\mathcal B$ 中每个节点从第 1 层到第 $L$$L$ 层的 embedding 。定义 $\mathcal{B}$$\mathcal B$ 子图的邻接矩阵为 ${\mathbf{A}}_{\mathcal{B},\mathcal{B}}$$\mathbf A_{\mathcal B,\mathcal B}$，它刻画了 $\mathcal{B}$$\mathcal B$ 内部的链接。可以看到 embedding 利用率是这个 batch 内链接的数量 $||{\mathbf{A}}_{\mathcal{B},\mathcal{B}}|{|}_0$$||\mathbf A_{\mathcal B,\mathcal B}||_0$ ，其中 $||\cdot |{|}_0$$||\cdot||_0$ 为矩阵的非零元素的个数。

   因此，为了最大化 embedding 利用率，我们应该设计一个 batch $\mathcal{B}$$\mathcal B$ 来最大化 batch 内链接的数量，这使得我们可以将 SGD 更新的效率和图聚类算法联系起来。

2. 现在我们正式地介绍 Cluster-GCN 。对于图 $G$$G$ ，我们将节点划分到 $C$$C$ 个分组：$\mathcal{V}=[{\mathcal{V}}_1,\cdots ,{\mathcal{V}}_C]$$\mathcal V = [\mathcal V_1,\cdots,\mathcal V_C]$ ，其中 ${\mathcal{V}}_c$$\mathcal V_c$ 由第 $c$$c$ 个分组的节点组成，$1\le c\le C$$1\le c\le C$ 。根据这一划分我们得到 $C$$C$ 个子图（subgraph）：

   $$\overline{G}=[G_1,\cdots ,G_C]=[({\mathcal{V}}_1,{\mathcal{E}}_1),\cdots ,({\mathcal{V}}_C,{\mathcal{E}}_C)]$$

   其中 ${\mathcal{E}}_c$$\mathcal E_c$ 由 ${\mathcal{V}}_c$$\mathcal V_c$ 中节点的链接组成。

   经过节点的重新排列之后，图 $G$$G$ 的邻接矩阵 $\mathbf{A}$$\mathbf A$ 被划分为 $C^2$$C^2$ 个子矩阵：

   $$\begin{array}{c}\mathbf{A}=\overline{\mathbf{A}}+\mathrm{\Delta }=\left[\begin{array}{cccc}{\mathbf{A}}_{1,1}& {\mathbf{A}}_{1,2}& \cdots & {\mathbf{A}}_{1,C}\\ {\mathbf{A}}_{2,1}& {\mathbf{A}}_{2,2}& \cdots & {\mathbf{A}}_{2,C}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathbf{A}}_{C,1}& {\mathbf{A}}_{C,2}& \cdots & {\mathbf{A}}_{C,C}\end{array}\right]\\ \overline{\mathbf{A}}=\left[\begin{array}{cccc}{\mathbf{A}}_{1,1}& \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{0}& {\mathbf{A}}_{2,2}& \cdots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ \mathbf{0}& \mathbf{0}& \cdots & {\mathbf{A}}_{C,C}\end{array}\right],\mathrm{\Delta }=\left[\begin{array}{cccc}\mathbf{0}& {\mathbf{A}}_{1,2}& \cdots & {\mathbf{A}}_{1,C}\\ {\mathbf{A}}_{2,1}& \mathbf{0}& \cdots & {\mathbf{A}}_{2,C}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathbf{A}}_{C,1}& {\mathbf{A}}_{C,2}& \cdots & \mathbf{0}\end{array}\right]\end{array}$$

   其中：

   • 每个对角块 ${\mathbf{A}}_{c,c}\in {\mathbb{R}}^{|{\mathcal{V}}_c|\times |{\mathcal{V}}_c|}$$\mathbf A_{c,c}\in \mathbb R^{|\mathcal V_c|\times |\mathcal V_c|}$ ，是子图 $G_c$$G_c$ 中的邻接矩阵。

   • $\overline{\mathbf{A}}$$\bar{\mathbf A}$ 为图 $\overline{G}$$\bar G$ 的邻接矩阵，$\overline{G}$$\bar G$ 是 $G$$G$ 经过分组之后移除组间的链接得到的新的图。

   • ${\mathbf{A}}_{s,t}$$\mathbf A_{s,t}$ 为分组 ${\mathcal{V}}_s$$\mathcal V_s$ 和 ${\mathcal{V}}_t$$\mathcal V_t$ 之间的链接。

   • $\mathrm{\Delta }$$\Delta$ 是由 $\mathbf{A}$$\mathbf A$ 的所有非对角线的块组成的矩阵。

   同样地，我们可以根据 $[{\mathcal{V}}_1,\cdots ,{\mathcal{V}}_C]$$[\mathcal V_1,\cdots,\mathcal V_C]$ 来划分节点特征为 $[{\mathbf{X}}_1,\cdots ,{\mathbf{X}}_C]$$[\mathbf X_1,\cdots,\mathbf X_C]$ ，以及划分节点label 为 $[{\mathbf{Y}}_1,\cdots ,{\mathbf{Y}}_C]$$[\mathbf Y_1,\cdots,\mathbf Y_C]$ 。其中 ${\mathbf{X}}_c$$\mathbf X_c$ 和 ${\mathbf{Y}}_c$$\mathbf Y_c$ 由 ${\mathcal{V}}_c$$\mathcal V_c$ 中节点的特征向量和 label 组成。

   现在我们用块对角矩阵 $\overline{\mathbf{A}}$$\bar{\mathbf A}$ 来近似 $\mathbf{A}$$\mathbf A$ ，即不考虑分组之间的链接。这种近似的好处是：目标函数可以划分为不同的cluster（每个 cluster 对应一个 batch）。

   令 $\overline{\mathbf{P}}$$\bar{\mathbf P}$ 为归一化的 $\overline{\mathbf{A}}$$\bar{\mathbf A}$ ，由于 $\overline{\mathbf{P}}$$\bar{\mathbf P}$ 的块对角形式，最终的 embedding 矩阵变为：

   $$\begin{array}{c}{\mathbf{Z}}^{(L)}=\overline{\mathbf{P}}\sigma \left(\overline{\mathbf{P}}\sigma (\cdots \overline{\mathbf{P}}\sigma \left(\overline{\mathbf{P}}\mathbf{X}{\mathbf{W}}^{(0)}\right){\mathbf{W}}^{(1)}\cdots )\right){\mathbf{W}}^{(L-1)}\\ =\left[\begin{array}{c}{\overline{\mathbf{P}}}_{1,1}\sigma \left({\overline{\mathbf{P}}}_{1,1}\sigma (\cdots {\overline{\mathbf{P}}}_{1,1}\sigma \left({\overline{\mathbf{P}}}_{1,1}{\mathbf{X}}_1{\mathbf{W}}^{(0)}\right){\mathbf{W}}^{(1)}\cdots )\right){\mathbf{W}}^{(L-1)}\\ ⋮\\ {\overline{\mathbf{P}}}_{C,C}\sigma \left({\overline{\mathbf{P}}}_{C,C}\sigma (\cdots {\overline{\mathbf{P}}}_{C,C}\sigma \left({\overline{\mathbf{P}}}_{C,C}{\mathbf{X}}_C{\mathbf{W}}^{(0)}\right){\mathbf{W}}^{(1)}\cdots )\right){\mathbf{W}}^{(L-1)}\end{array}\right]\end{array}$$

   其中 ${\overline{\mathbf{P}}}_{c,c}$$\bar{\mathbf P}_{c,c}$ 为 $\overline{\mathbf{P}}$$\bar{\mathbf P}$ 的第 $c$$c$ 个对角块。

   因此损失函数可以分解为：

   $$\begin{array}{c}{\mathcal{L}}_{\overline{\mathbf{P}}}=\sum _c\frac{|{\mathcal{V}}_c|}{n}{\mathcal{L}}_{{\overline{\mathbf{P}}}_{c,c}}\\ {\mathcal{L}}_{{\overline{\mathbf{P}}}_{c,c}}=\frac{1}{|{\mathcal{V}}_c|}\sum _{v\in {\mathcal{V}}_c}f(y_v,{\overrightarrow{\mathbf{z}}}_v^{(L)})\end{array}$$

   在每一步我们随机采样一个簇 ${\mathcal{V}}_c$$\mathcal V_c$ ，然后根据 ${\mathcal{L}}_{{\overline{\mathbf{P}}}_{c,c}}$$\mathcal L_{\bar{\mathbf P}_{c,c}}$ 的梯度来进行 SGD 更新。在这个更新过程中，仅依赖于当前 batch 的子图 ${\mathbf{A}}_{c,c}$$\mathbf A_{c,c}$ 、子样本特征 ${\mathbf{X}}_c$$\mathbf X_c$ 、子样本的 label ${\mathbf{Y}}_c$$\mathbf Y_c$ 以及模型 ${\left\{{\mathbf{W}}^{(l)}\right\}}_{0=1}^L$$\left\{\mathbf W^{(l)}\right\}_{0=1}^L$ 。

   可以看到，Cluster-GCN 仅需要进行矩阵乘法和前向/反向传播，而之前的 SGD-based 方法中需要对邻域进行搜索，因此我们的方法更容易实现。

3. Cluster-GCN 使用图聚类算法对图进行分组。图聚类算法（如 Metis 和 Graclus）旨在对图的节点进行划分，使得簇内的链接比簇间的链接更多，从而更好地捕获图的聚类和社区结构。这正是我们需要的结果，因为：

   • 如前所述， embedding 利用率等于每个 batch 的batch 内链接数量。

   • 由于我们用块对角矩阵 $\overline{\mathbf{A}}$$\bar{\mathbf A}$ 来近似替代邻接矩阵 $\mathbf{A}$$\mathbf A$ ，其近似误差正比于簇间链接 $\mathrm{\Delta }$$\Delta$ 。所以我们需要找到一个划分，从而最大程度地减少簇间链接的数量。

4. 下图给出了在完整图 $G$$G$ （左图）以及聚类图 $\overline{G}$$\bar G$ （右图）上的邻域扩展。红色节点是扩展的起始节点，不同颜色代表不同的 hop 。

   可以看到：Cluster-GCN 可以避免繁重的邻域搜索，从而将精力集中在每个簇内的邻居上。

   

5. 我们比较了两种不同的节点划分策略：随机划分（random partition）、聚类划分（clustering partition）。

   我们分别通过随即划分、METIS 聚类划分将图划分为 10 个分组，然后每个分组作为一个 batch 来执行 SGD 更新。数据集为三个 GCN 公共数据集，评估指标为测试集 F-1 score。可以看到：在相同 epoch 下，使用聚类划分可以获得更高的准确性。这表明使用图聚类很重要，并且不应该使用随机划分。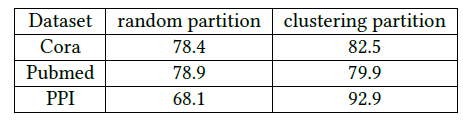

   

6. 算法复杂度：由于仅考虑 ${\mathcal{V}}_c$$\mathcal V_c$ 的内部链接，因此不需要执行 ${\mathbf{A}}_{c,c}$$\mathbf A_{c,c}$ 之外的邻域搜索。因此每个 batch 的复杂度仅有矩阵乘法 ${\overline{\mathbf{P}}}_{c,c}{\mathbf{H}}_c^{(l)}{\mathbf{W}}^{(l)}$$\bar{\mathbf P}_{c,c} \mathbf H_c^{(l)} \mathbf W^{(l)}$ ，以及某些逐元素的运算来决定。因此每个 batch 的时间复杂度为 $O(||{\mathbf{A}}_{c,c}|{|}_{0}d+b{d}^2)$$O(||\mathbf A_{c,c}||_0 d + b d^2)$ ， $||{\mathbf{A}}_{c,c}|{|}_0$$||\mathbf A_{c,c}||_0$ 为 ${\mathcal{V}}_c$$\mathcal V_c$ 内部链接的数量。因此每个 epoch 的时间复杂度为 $O(||\mathbf{A}|{|}_{0}d+n{d}^2)$$O(||\mathbf A||_0 d + nd^2)$ ， $||\mathbf{A}|{|}_0$$||\mathbf A||_0$ 为 $G$$G$ 的边的数量。

   平均而言，每个 batch 只需要计算 $O(bL)$$O(bL)$ 个 embedding，它是线性的而不是 $L$$L$ 的指数。因此每个batch 的空间复杂度为 $O(bLd)$$O(bLd)$ ，它具有比所有之前算法更高的内存效率。

   另外，我们的算法仅需要将子图加载到 GPU 内存中，无需加载整个图（虽然整个图的存储通常不是瓶颈）。

   我们在下表中总结了时间复杂度和空间复杂度。显然，所有 SGD-based 算法在层数方面都是指数复杂度。对于 VR-GCN，即使 $r$$r$ 很小，它也可以导致巨大的空间复杂度，即，可能超出 GPU 的内存容量。

   接下来我们介绍我们的 Cluster-GCN 算法，它兼顾了 full-batch 梯度下降下每个 epoch 的时间复杂度、以及在普通 SGD 梯度下降下的空间复杂度。

   其中：$L$$L$ 为层数，$m=||\mathbf{A}|{|}_0$$m=||\mathbf A||_0$ 为邻接矩阵中的非零数量（也是边的数量），$d$$d$ 为 embedding 维度（为方便起见，所有层的 embedding以及输入特征的维度都是 $d$$d$ ），$n$$n$ 为节点数量，$D$$D$ 为平均的 node degree ，$b$$b$ 为 mibi-batch size ，$r$$r$ 为邻域采样大小。

   $$\begin{array}{ccc}& \text{TimeComplexity}& \text{MemoryComplexity}\\ \text{GCN}& O(Lmd+Ln{d}^2)& O(Lnd+L{d}^2)\\ \text{Vanilla SGD}& O\left(D^{L}n{d}^2\right)& O(b{D}^{L}d+L{d}^2)\\ \text{GraphSAGE}& O\left(r^{L}n{d}^2\right)& O(b{r}^{L}d+L{d}^2)\\ \text{FastGCN}& O\left(rLn{d}^2\right)& O(brLd+L{d}^2)\\ \text{VR-GCN}& O(Lmd+Ln{d}^2+r^{L}n{d}^2)& O(Lnd+L{d}^2)\\ \text{Cluster-GCN}& O(Lmd+Ln{d}^2)& O(bLd+L{d}^2)\end{array}$$

   注意：

   • 由于采用了方差缩减技术，VR-GCN 的 $r$$r$ 可以远小于 GraphSAGE 和 FastGCN。

   • 对于空间复杂度，$L{d}^2$$Ld^2$ 是用于存储模型参数 ${\left\{{\mathbf{W}}^{(l)}\right\}}_{l=1}^L$$\left\{\mathbf W^{(l)}\right\}_{l=1}^L$ ，其它项是用于存储 embedding 。

   • 为简单起见，我们忽略了存储Graph 以及子图的需求，因为它们通常都是固定的，且通常不是主要瓶颈。

   • Cluster-GCN 具有最好的计算复杂度和最好的空间复杂度。

     从实验部分得知，Cluster-GCN 的最大优势是内存需求更小从而可以扩展到更大的图。训练速度和训练准确率方面，Cluster-GCN 和 VR-GCN 各有优势（在不同的层数方面）。

1.1.2 随机多重聚类 SMC

1. 尽管前述的 Cluster-GCN 实现了良好的计算复杂度和空间复杂度，但是仍然有两个潜在的问题：

   • 对图进行划分之后，某些链接被删除了（即 $\mathrm{\Delta }$$\Delta$ 的部分），因此模型的性能可能受到影响。

   • 图聚类算法倾向于将相似的节点聚合在一起，因此每个batch 的节点分布和原始数据集不一致，从而导致在 SGD 更新时，batch 的梯度是完整梯度的一个有偏的估计。

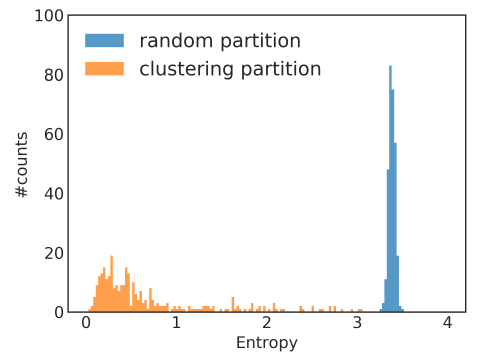
   我们以 Reddit 数据集为例，考察随机划分来选择 mini-batch 、通过 Metis 聚类算法选择 mini-batch 的数据分布的差异，划分数量为 300 个分区。数据分布以batch 内节点标签分布的熵来衡量。我们给出不同batch 的标签熵（label entropy）的分布直方图如下所示，可以看到：

   • 大多数聚类batch 具有较低的标签熵，这表明聚类的 batch 倾向于某些特定的 label，从而与整体的数据分布不一致。这可能会影响 SGD 算法的收敛性。

   • 随机batch 具有较高的标签熵，这表明随机 batch 的数据分布和整体数据分布更为一致。

   

2. 为解决这些问题，我们提出了一个随机多重聚类框架（stochastic multiple clustering: SMC），该框架通过随机合并多个簇，从而减少 batch 之间的数据分布差异。

   我们首先将节点划分到 $C$$C$ 个分组：$\mathcal{V}=[{\mathcal{V}}_1,\cdots ,{\mathcal{V}}_C]$$\mathcal V = [\mathcal V_1,\cdots,\mathcal V_C]$ ，其中 $C$$C$ 较大。然后每次构建一个 batch $\mathcal{B}$$\mathcal B$ 时，我们并不是考虑一个簇，而是随机选择 $q$$q$ 个簇，记作 $c_1,\cdots ,c_q$$c_1,\cdots,c_q$ ，因此这个 batch $\mathcal{B}=\{{\mathcal{V}}_{c_1},\cdots ,{\mathcal{V}}_{c_q}\}$$\mathcal B =\{\mathcal V_{c_1},\cdots, \mathcal V_{c_q}\}$ 。此外，部分簇间链接也被考虑在内，这些簇间链接为：$\{{\mathbf{A}}_{i,j}\mid i,j\in c_1,\cdots ,c_q\}$$\{\mathbf A_{i,j}\mid i,j\in c_1,\cdots,c_q\}$ 。

   通过这种方式，所有簇间链接将被重新合并到模型中，并且簇的随机组合可以使得 batch 之间的数据分布的差异更小。

   这种随机多重聚类框架如下图所示，每个 batch 包含 2 个簇，相同的 batch 的簇具有相同的颜色。不同的epoch 中选择不同的簇组合。

   这种方法只能缓解问题，但是无法解决问题。因为即使是随机组合多个簇，新的 batch 内节点分布与整体分布仍然是有差异的。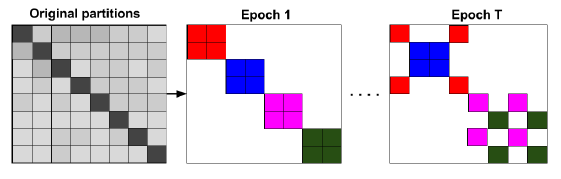

   

3. 我们在 Reddit 数据集上进行实验，对比了 SMC 和普通 Cluster-GCN 的效果。在 Cluster-GCN 中我们选择划分为 300 个分区，在 SMC 中我们选择划分为 1500 个分区并随机选择 5 个簇来构成一个 batch。

   实验结果如下图所示，其中 x 轴为 epoch， y 轴为 F1-score 。可以看到随机多重聚类可以显著改善 Cluster-GCN 的收敛性。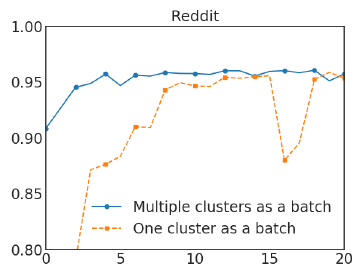

   

4. Cluster-GCN 算法：

   • 输入：

     • 图 $G(\mathcal{V},\mathcal{E},\mathbf{A})$$G(\mathcal V,\mathcal E, \mathbf A)$

     • 输入特征矩阵 $\mathbf{X}$$\mathbf X$

     • 节点标签矩阵 $\mathbf{Y}$$\mathbf Y$ （每行代表一个节点标签的 one-hot 或者 multi-hot 向量）

     • 最大迭代步 max-iter

     • 划分簇的数量 $C$$C$

     • 每个 batch 的簇的数量 $q$$q$

   • 输出：模型的参数 ${\left\{{\mathbf{W}}^{(l)}\right\}}_{l=1}^L$$\left\{\mathbf W^{(l)}\right\}_{l=1}^L$ 以及节点的embedding 矩阵 ${\mathbf{H}}^{(L)}$$\mathbf H^{(L)}$

   • 算法步骤：

     • 通过 METIS 聚类算法划分 $\mathcal{V}$$\mathcal V$ 到 $C$$C$ 个簇：${\mathcal{V}}_1,\cdots ,{\mathcal{V}}_C$$\mathcal V_1,\cdots,\mathcal V_C$ 。

     • 迭代：$\text{iter}=1,2,\cdots ,\text{max-iter}$$\text{iter} = 1,2,\cdots,\text{max-iter}$，迭代过程：

       • 随机无放回选择 $q$$q$ 个簇 $\{{\mathcal{V}}_{c_1},\cdots ,{\mathcal{V}}_{c_q}\}$$\{\mathcal V_{c_1},\cdots,\mathcal V_{c_q}\}$ 。

       • 以节点集合 $\overline{\mathcal{V}}={\mathcal{V}}_{c_1}\cup \cdots \cup {\mathcal{V}}_{c_q}$$\bar{\mathcal V} = \mathcal V_{c_1}\cup\cdots\cup\mathcal V_{c_q}$ 构建子图 $\overline{G}$$\bar G$ ，以及子图的邻接矩阵 ${\mathbf{A}}_{\overline{\mathcal{V}},\overline{\mathcal{V}}}$$\mathbf A_{\bar{\mathcal V}, \bar{\mathcal V}}$ 。

       • 根据子图的损失函数来计算梯度 $\overrightarrow{\mathbf{g}}=\mathrm{\nabla }{\mathcal{L}}_{{\mathbf{A}}_{\overline{\mathcal{V}},\overline{\mathcal{V}}}}$$\mathbf{\vec g} = \nabla \mathcal L_{\mathbf A_{\bar{\mathcal V}, \bar{\mathcal V}}}$ 。

       • 基于 Adam 优化算法使用梯度 $\overrightarrow{\mathbf{g}}$$\mathbf{\vec g}$ 来更新参数。

     • 输出模型的参数 ${\left\{{\mathbf{W}}^{(l)}\right\}}_{l=1}^L$$\left\{\mathbf W^{(l)}\right\}_{l=1}^L$ 以及节点的embedding 矩阵 ${\mathbf{H}}^{(L)}$$\mathbf H^{(L)}$ 。

5. METIS 是 Karypis Lab 开发的一个功能强大的图切分软件包，支持多种切分方式。优势：

   • METIS 具有高质量的划分结果，据称比常规的谱聚类要准确 10% ~ 50% 。

   • METIS 执行效率非常高，比常见的划分算法块 1~2 个数量级。百万规模节点的图通常几秒钟之内就可以切分为 256 个簇。

   • METIS 具有很低的空间复杂度和时间复杂度，从而降低了存储负载和计算量。

1.1.3 深层 GCN

1. GCN 原始论文表明：对 GCN 使用更深的层没有任何效果。但是，实验中的这些数据集太小，可能没有说服力。例如，实验中只有数百个节点的图，太深的GCN 可能会导致严重过拟合。

   另外，我们观察到更深的 GCN 模型的优化变得更困难，因为更深的模型可能会阻碍前几层的消息传递。在原始 GCN 中，他们采用类似于残差连接的技术，使得模型能够将信息从前一层传递到后一层。具体而言，第 $l+1$$l+1$ 层的卷积层为：

   $$\begin{array}{c}{\mathbf{Z}}^{(l+1)}=\mathbf{P}{\mathbf{H}}^{(l)}{\mathbf{W}}^{(l)}\\ {\mathbf{H}}^{(l+1)}=\sigma \left({\mathbf{Z}}^{(l+1)}\right)+{\mathbf{H}}^{(l)}\end{array}$$

   这里我们提出另一种简单的技术来改善深层 GCN 的训练。在原始 GCN 中，每个节点都聚合了来自前一层邻域的representation。但是在深层 GCN 的背景下，该策略可能不太合适，因为它没有考虑深度。

   凭直觉，附近的邻居应该比远处的节点贡献更大。因此我们提出了一种更好的解决该问题的技术：放大邻接矩阵 $\mathbf{A}$$\mathbf A$ 的对角线部分，这样我们每个 GCN 层的聚合把更大的权重放到前一层的 representation 上。即：

   $$\begin{array}{c}{\mathbf{Z}}^{(l+1)}=(\mathbf{P}+\mathbf{I}){\mathbf{H}}^{(l)}{\mathbf{W}}^{(l)}\\ {\mathbf{H}}^{(l+1)}=\sigma \left({\mathbf{Z}}^{(l+1)}\right)\end{array}$$

2. 这种方式看起来似乎合理，但是这对所有节点都使用相同的权重，无论其邻居数量是多少，这现得有些不合适。此外，当使用更深的层时，某些数值可能出现指数型增长，可能会导致数值不稳定。因此我们提出修改版，从而更好地维护邻域信息和数值范围。

   我们首先将一个单位矩阵添加到原始的 $\mathbf{A}$$\mathbf A$ 中并进行归一化：

   $$\tilde{\mathbf{P}}=(\mathbf{D}+\mathbf{I}{)}^{-1/2}(\mathbf{A}+\mathbf{I})(\mathbf{D}+\mathbf{I}{)}^{-1/2}$$

   $\tilde{\mathbf{P}}$$\tilde{\mathbf P}$ 就是带自环的归一化矩阵。

   然后对消息进行传播：

   $$\begin{array}{c}{\mathbf{Z}}^{(l+1)}=(\tilde{\mathbf{P}}+\lambda \text{diag}\left(\tilde{\mathbf{P}}\right)){\mathbf{H}}^{(l)}{\mathbf{W}}^{(l)}\\ {\mathbf{H}}^{(l+1)}=\sigma \left({\mathbf{Z}}^{(l+1)}\right)\end{array}$$

   其中 $\lambda$$\lambda$ 为超参数， $\text{diag}(\tilde{\mathbf{P}})$$\text{diag}(\tilde{\mathbf P})$ 为 $\tilde{\mathbf{P}}$$\tilde{\mathbf P}$ 对角线组成的对角矩阵。

   实验表明这种对角线增强（diagonal enhancement）技术可以帮助构建更深的 GCN 并达到 SOTA 性能。

   这就是人工构造的 attention：对 self 施加相对更大的重要性（这意味着对邻居施加更小的重要性）。可以通过 GAT 来自适应地学习 self 和邻居的重要性。

   根据论文的实验，当层数很深时，模型效果退化并且训练时间大幅上涨，因此没有任何意义。所以这一小节的内容没有价值。

1.2 实验

1. 我们在两种任务上评估了 Cluster-GCN 的效果：在四个公共数据集上的 multi-label 分类任务和 multi-class 分类任务。这些数据集的统计信息如下表所示。

   注意：

   • Reddit 数据集是迄今为止我们所看到的最大的 GCN 公共数据集。

   • 而 Amazon2M 数据集是我们自己收集的，比 Reddit 数据集更大。

   

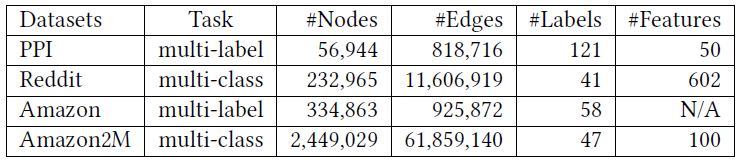
   这些数据集的 training/validation/test 拆分如下表所示：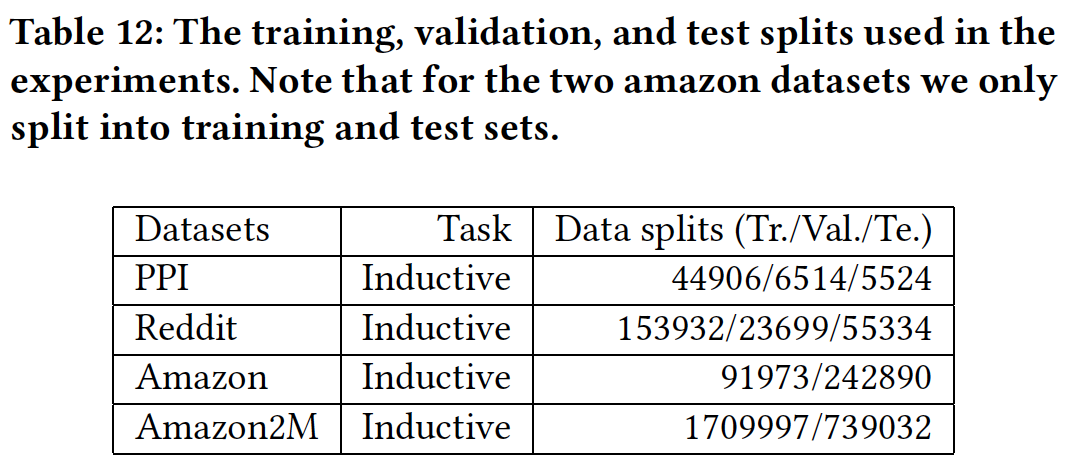

   

2. baseline 方法：我们比较了以下 SOTA 的 GCN 训练算法以及 Cluster-GCN 方法：

   • VRGCN：保留图中所有节点的历史embedding 均值，并仅采样少数几个邻居来加快训练速度。我们采用原始论文中的建议，将采用邻居数量设为 2 。

   • GraphSAGE：对每个节点采样固定数量的邻居。我们使用原始论文中默认的邻居数量 ：双层GCN 第一层、第二层采样数量分别为 $D^{(1)}=25,D^{(2)}=10$$D^{(1)} = 25, D^{(2)} = 10$ 。

   由于原始 GCN 很难扩展到大图，因此我们不比较原始 GCN 。根据 VRGCN 论文所述，VRGCN 比 FastGCN 更快，因此我们也不比较 FastGCN。

3. 实验配置：我们使用 PyTorch 实现了 Cluster-GCN。对于其它baseline，我们使用原始论文提供的代码。

   • 所有方法都采用 Adam 优化器，学习率为 0.01，dropout 比例为20%，权重衰减 weight decay 为零。

   • 所有方法都采用均值聚合，并且隐层维度都相同。

   • 所有方法都使用相同的 GCN 结构。

   • 在比较过程种我们暂时不考虑 diagonal enhancement 之类的技术。

   • 对于 VRGCN 和 GraphSAGE ，我们遵循原始论文种提供的配置，并将 batch-size 设为 512 。

   • 对于 Cluster-GCN，下表给出了每个数据集的分区数量，以及每个 batch 的簇的数量。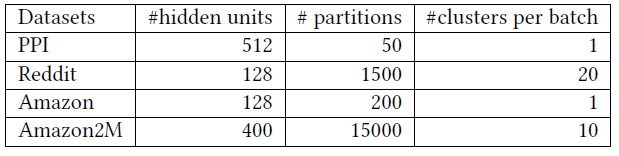

     

   • 所有实验均在 20 核的 Intel Xeon CPU(2.20 GHz) + 192 GB 内存 + NVIDIA Tesla V100 GPU(16GB RAM) 上执行。

   注意：在 Cluster-GCN 种，聚类算法被视为预处理步骤，并且未被计入训练时间。聚类只需要执行一次，并且聚类时间很短。

   此外，我们遵从FastGCN 和 VR-GCN 的工作，对 GCN 的第一层执行 $\mathbf{A}\mathbf{X}$$\mathbf A\mathbf X$ 的预计算（pre-compute），这使得我们节省了第一层昂贵的邻域搜索过程。

   为了用于 inductive setting，其中测试节点在训练期间不可见，我们构建了两个邻接矩阵：一个邻接矩阵仅包含训练节点，另一个邻接矩阵包含所有节点。图划分仅作用在第一个邻接矩阵上。

   为了计算内存用量，对于 TensorFlow 我们使用 tf.contrib.memory_stats.BytesInUse()，对于 PyTorch 我们使用 torch.cuda.memory_allocated() 。

1.2.1 中等规模数据集

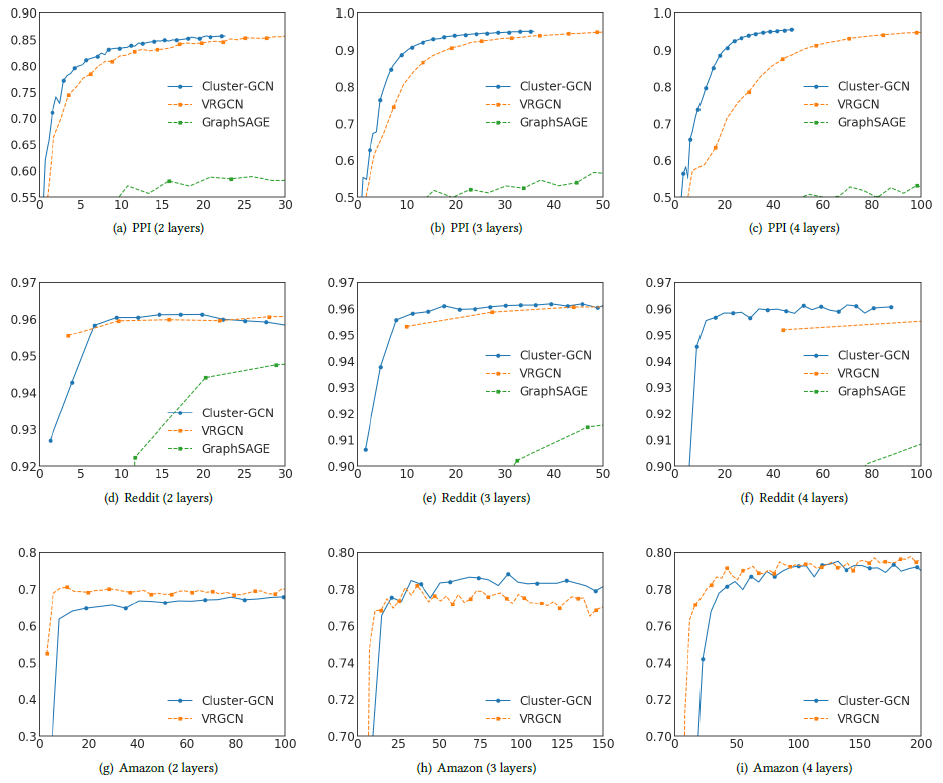
1. 我们首先在训练速度和训练准确性方面评估 Cluster-GCN。我们给出两层GCN、三层GCN、四层 GCN 在三个中等规模数据集PPI、Reddit、Amazon 上的训练时间和预测准确性，如下图所示。其中 x 轴为训练时间（单位秒），y 轴为验证集准确性（单位 F1-Score）。

   由于 GraphSAGE 比 VRGCN、Cluster-GCN 更慢，因此 GraphSAGE 的曲线仅出现在 PPI、Reddit 数据集上。

   对于 Amazon 数据集，由于没有节点特征，因此我们用一个单位矩阵 $\mathbf{I}$$\mathbf I$ 来作为特征矩阵 $\mathbf{X}$$\mathbf X$ 。在此配置下，参数矩阵 ${\mathbf{W}}^{(0)}$$\mathbf W^{(0)}$ 的维度为 334863 x 128 。因此，计算主要由稀疏矩阵运算决定（如 $\mathbf{A}{\mathbf{W}}^{(0)}$$\mathbf A \mathbf W^{(0)}$） 。

   结论：

   • 在 PPI 和 Reddit 数据集中，Cluster-GCN 的训练速度最快，同时预测准确性也最好。

   • 在 Amazon 数据集中，Cluster-GCN 训练速度比 VRGCN 更慢，预测准确性除了三层GCN 最高以外都差于 VRGCN 。

   

2. Cluster-GCN 比 VRGCN 更慢的原因可能是：不同框架的稀疏矩阵的运算速度不同。VRGCN 在Tensorflow 中实现，而 Cluster-GCN 在 PyTorch 中实现。PyTorch 中的稀疏张量支持目前处于早期阶段。

   下表中我们显示了 Tensorflow 和 PyTorch 对于 Amazon 数据集执行前向、反向操作的时间，并使用一个简单的、两层线性网络对这两个框架进行基准测试，括号中的数字表示隐层的维度。我们可以清楚地看到Tensorflow 比 PyTorch 更快。当隐层维度更高时，差异会更大。这解释了为什么 Cluster-GCN 在Amazon 数据集中训练时间比 VRGCN 更长。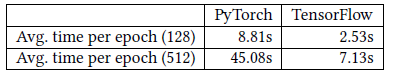

   

3. 对于GCN 而言，除了训练速度以外，内存需求通常更重要，因为这将直接限制了算法的可扩展性。

   • 内存需求包括训练多个 epoch 所需的内存。为加快训练速度，VRGCN 需要在训练过程中保持历史 embedding，因此和 Cluster-GCN 相比 VRGCN 需要更多的内存。

   • 由于指数级邻域扩展的问题，GraphSAGE 也比 Cluster-GCN 需要更多的内存。

   下表中，我们给出了不同方法在不同数据集上训练两层GCN、三层GCN、四层 GCN 所需要的内存。括号中的数字表示隐层的维度。可以看到：

   • 当网络更深时，Cluster-GCN 的内存使用并不会增加很多。因为每当新增一层，引入的额外变量是权重矩阵 ${\mathbf{W}}^{(L)}$$\mathbf W^{(L)}$ ，相比较于子图以及节点特征，它需要的内存较少。

   • 尽管 VRGCN 只需要保持每一层的历史 embedding 均值，但是这些 embedding 通常都是稠密向量。因此随着层的加深，它们很快统治了内存需求。

   • Cluster-GCN 比 VRGCN 有更高的内存利用率。如在 Reddit 数据集上训练隐层维度为 512 的四层 GCN 时，VRGCN 需要 2064MB 内存，而 Cluster-GCN 仅需要 308MB 内存。

   

1.2.2 大规模数据集

1. 迄今为止评估GCN 的最大的公共数据集是 Reddit 数据集，其统计数据如前所述。Reddit 数据集大约包含 200K 个节点，可以在几百秒之内训练 GCN 。

   为测试 GCN 训练算法的可扩展性，我们基于 Amazon co-purchasing 网络构建了一个更大的图，图中包含 200 万节点、6100 万边。原始的 co-purchase 数据来自于 Amazon-3M 。

   图中每个节点都是一个商品，图中的连接表示是否同时购买了两个商品。每个节点特征都是从商品描述文本中抽取的 bag-of-word ，然后通过 PCA 降维到 100 维。此外，我们使用 top-level 的类别作为节点的label 。下表给出了数据集中频次最高的类别：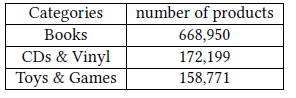

   

2. 我们在这个大型数据集上比较了 Cluster-GCN 和 VRGCN 的训练时间、内存使用、测试准确性（F1-Score 来衡量）。

   可以看到：

   • 训练速度：对于两层GCN ，VRGCN 训练速度更快；但是对于更深的GCN，Cluster-GCN 训练速度更快。

   • 内存使用：VRGCN 比 Cluster-GCN 需要多得多的内存，对于三层GCN 时VRGCN 所需内存是 Cluster-GCN 的五倍。当训练四层GCN 时 VRGCN 因为内存耗尽而无法训练。

   • 测试准确性：Cluster-GCN 在四层GCN 时可以达到该数据集上的最佳准确性。

   

1.2.3 深层 GCN

1. 这里我们考虑更深层的 GCN。我们首先给出 Cluster-GCN 和 VRGCN 在 PPI 数据集上不同深度的训练时间的比较，其中每种方法都训练 200 个 epoch 。

   可以看到：VRGCN 的训练时间因为其代价较高的邻域发现而呈现指数型增长，而 Cluster-GCN 的训练时间仅线性增长。

   

2. 然后我们研究更深的GCN 是否可以得到更好的准确性（衡量指标为验证集的 F1-score ）。我们在 PPI 数据集上进行实验并训练 200 个 epoch ，并选择dropout rate = 0.1 。其中：

   • Cluster-GCN with (1) 表示：原始的 Cluster-GCN。

   • Cluser-GCN with (10) 表示：考虑如下的 Cluster-GCN：

     $$\begin{array}{c}\tilde{\mathbf{P}}=(\mathbf{D}+\mathbf{I}{)}^{-1/2}(\mathbf{A}+\mathbf{I})(\mathbf{D}+\mathbf{I}{)}^{-1/2}\\ {\mathbf{Z}}^{(l+1)}=\tilde{\mathbf{P}}{\mathbf{H}}^{(l)}{\mathbf{W}}^{(l)}\\ {\mathbf{H}}^{(l+1)}=\sigma \left({\mathbf{Z}}^{(l+1)}\right)\end{array}$$

   • Cluster-GCN with (10) + (9) 表示：考虑如下的 Cluster-GCN：

     $$\begin{array}{c}\tilde{\mathbf{P}}=(\mathbf{D}+\mathbf{I}{)}^{-1/2}(\mathbf{A}+\mathbf{I})(\mathbf{D}+\mathbf{I}{)}^{-1/2}\\ {\mathbf{Z}}^{(l+1)}=(\tilde{\mathbf{P}}+\mathbf{I}){\mathbf{H}}^{(l)}{\mathbf{W}}^{(l)}\\ {\mathbf{H}}^{(l+1)}=\sigma \left({\mathbf{Z}}^{(l+1)}\right)\end{array}$$

   • Cluster-GCN with (10) + (11) 表示：考虑如下的 Cluster-GCN：

     $$\begin{array}{c}\tilde{\mathbf{P}}=(\mathbf{D}+\mathbf{I}{)}^{-1/2}(\mathbf{A}+\mathbf{I})(\mathbf{D}+\mathbf{I}{)}^{-1/2}\\ {\mathbf{Z}}^{(l+1)}=(\tilde{\mathbf{P}}+\lambda \text{diag}\left(\tilde{\mathbf{P}}\right)){\mathbf{H}}^{(l)}{\mathbf{W}}^{(l)}\\ {\mathbf{H}}^{(l+1)}=\sigma \left({\mathbf{Z}}^{(l+1)}\right)\end{array}$$

     其中 $\text{diag}(\tilde{\mathbf{P}})$$\text{diag}(\tilde{\mathbf P})$ 为 $\tilde{\mathbf{P}}$$\tilde{\mathbf P}$ 对角线组成的对角矩阵。

   可以看到：

   • 对于2 层到 5 层，所有方法的准确性都随着层深度的增加而提升，这表明更深的 GCN 可能是有效的。

   • 当使用 7 层或 8 层时，前三种方法无法在 200 个 epoch 内收敛，并会大大降低准确性。可能的原因是针对更深GCN 的优化变得更加困难。其中红色的数字表示收敛性很差。

     即使是第四种方法，它在层数很深时虽然收敛，但是模型效果下降、训练时间暴涨（根据前面的实验），因此没有任何意义。

     此外，原始 Cluster-GCN 在五层时达到最好的效果，所以对角增强技术失去了价值。

   

3. 为考察更深层GCN 的详细收敛性，我们给出了采用对角增强技术（即 ${\mathbf{Z}}^{(l+1)}=(\tilde{\mathbf{P}}+\lambda \text{diag}\left(\tilde{\mathbf{P}}\right)){\mathbf{H}}^{(l)}{\mathbf{W}}^{(l)}$$\mathbf Z^{(l+1)} = \left(\tilde{\mathbf P} + \lambda \text{diag}\left(\tilde{\mathbf P}\right)\right)\mathbf H^{(l)} \mathbf W^{(l)}$ ） 之后，八层的GCN 在不同 epoch 上的验证准确性（F1-Score）。

   可以看到：我们提出的对角增强技术可以显著改善模型的收敛性，并得到较好的准确性。

   

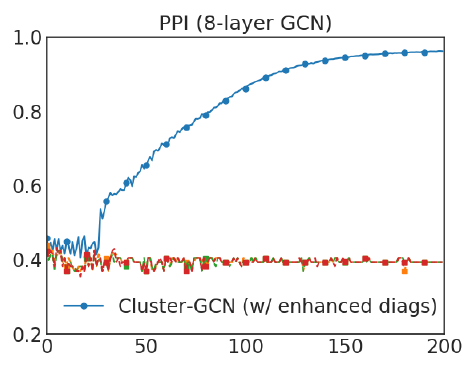
4. 采用了对角增强技术的 Cluster-GCN 能够训练更深的 GCN 从而达到更好的准确性（F1-Score）。我们在下表中给出不同模型在不同数据集上的测试F1-Score。

   可以看到：

   • 在 PPI 数据集上，Cluter-GCN 通过训练一个具有 2048 维的隐层的 5 层 GCN 来取得 SOTA 效果。

   • 在 Reddit 数据集上，Cluster-GCN 通过训练一个具有 128 维隐层的4 层 GCN 取得 SOTA 效果。

   这个优势并不是对角增强技术带来的，而是因为 Cluster-GCN 的内存需求更少从而允许训练更深的模型，而更深的模型通常效果更好。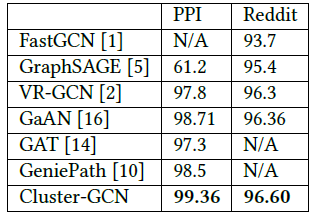

   

5. 前面的实验都未考虑 ClusterGCN 的预处理时间（如，数据集加载，graph clustering 等等）。这里我们给出 Cluster-GCN 在四个数据集上的预处理时间的细节。对于 graph clustering，我们使用 Metis 。结果如下表所示。可以看到：

   • graph clustering 算法仅占用预处理时间的很小比例。

   • graph clustering 可以扩展到大型的数据集。

   此外，graph clustering 仅需要执行一次，并且之后被后续的训练过程重复使用。