一、GDCN [2023]

《Towards Deeper, Lighter and Interpretable Cross Network for CTR Prediction》

1. 有效地建模feature interactions 对于提高CTR 模型的预测性能至关重要。然而，现有的方法面临三个重大挑战：

   • 首先，虽然大多数方法可以自动捕获高阶feature interactions ，但随着feature interactions 的阶次增加，它们的性能往往会下降。

   • 其次，现有方法缺乏能力对预测结果提供令人信服的解释，特别是对于高阶feature interactions ，这限制了其预测的可信度。

   • 第三，许多方法都存在冗余参数，特别是在embedding layer 中。

   本文提出了一种称为Gated Deep Cross Network (GDCN) 的新方法，以及一种Field-level Dimension Optimization (FDO) 方法来应对这些挑战。作为GDCN 的核心结构，Gated Cross Network (GCN) 捕获显式的高阶feature interactions，并在每个阶次中使用information gate 来动态地过滤important interactions 。此外，我们使用FDO 方法，根据每个field 的重要性来学习condensed dimensions 。在五个数据集上进行的综合实验证明了GDCN 的有效性、优越性和可解释性。此外，我们验证了FDO 在learning various dimensions 和reducing model parameters 方面的有效性。

2. 大多数CTR 建模方法通常由三种layer 组成：feature embedding, feature interaction, and prediction 。为了提高CTR 预测的准确性，人们已经提出了许多专注于设计有效feature interaction 架构的方法。然而，以前的工作，如Logistic Regression (LR) 和FM-based 的方法，只能建模低阶feature interactions 或固定阶次的feature interactions 。随着互联网规模的推荐系统变得越来越复杂，对捕获高阶feature interactions 的方法的需求日益增长。因此，一些最新的方法能够对显式的和隐式的高阶feature interactions 进行联合建模，并实现显著的性能改进。虽然这些方法取得了很大进展，但它们仍然有三个主要局限性：

   • 首先，随着feature interactions 阶次的增加，这些方法的有效性趋于下降。一般来说，所能够捕获的交互的最大阶次由feature interactions 的depth 决定。随着interaction layers 的加深，interactions 的数量呈指数增长，这使得模型能够生成更多的高阶交互。然而，并不是所有的交互都是有帮助的，这也带来了许多不必要的交互，导致性能下降和计算复杂度增加。许多现有的SOTA 工作已经通过hyper-parameter analysis 证实，当交互阶次超过一定深度（通常是三阶）时，它们的性能会下降。因此，至关重要的是进行改进从而确保高阶交互具有positive 影响，而不是引入更多噪音并导致次优性能。

   • 其次，现有方法缺乏可解释性，限制了其predictions and recommendations 的可信度。大多数方法由于隐式的feature interactions （通过DNN）、或为所有feature interactions 分配相等的权重，从而导致可解释性较低。尽管一些方法（《DCAP: Deep Cross Attentional Product Network for User Response Prediction》、《Interpretable click-through rate prediction through hierarchical attention》、《Autoint: Automatic feature interaction learning via selfattentive neural networks》 ）试图通过self-attention 机制学到的attention scores 来提供解释，但这种方法倾向于融合（fuse）所有features information ，因此很难区分哪些交互是必不可少的，尤其是对于高阶的crosses 。因此，开发方法能够从模型的和实例的角度来提供有说服力的解释，至关重要，从而实现更可靠的、更可信的结果。

   • 第三，大多数现有模型包含大量冗余参数，尤其是在embedding layer 中。许多方法依赖于feature-wise 的交互结构，这些结构假设所有fields 的embedding dimensions 是相等的。然而，考虑到fields 的信息容量，有些fields 只需要相对较短的维度。因此，这些模型在embedding layer 产生大量冗余参数。但直接降低embedding 维度会导致模型性能下降。同时，大多数方法仅侧重于减少non-embedding 参数，与减少embedding 参数相比，对整体参数减少的影响并不显著。尽管DCN 和DCN-V2 使用经验公式为每个field 分配不同的维度，该公式仅基于feature numbers 来计算维度，但它们忽略了每个field 的重要性，并且经常无法减少模型参数。因此，我们的目标是为每个field 分配field-specific and condensed dimensions ，考虑其固有的重要性，并有效减少embedding 参数。

   本文提出了一种称为Gated Deep Cross Network (GDCN) 的模型、以及一种称为Field-level Dimension Optimization (FDO) 的方法来解决上述限制。在DCN-V2 优雅而高效的设计的基础上，GDCN 进一步提高了低阶交互和高阶交互的性能，并且在模型的和实例的视角下都表现出了很好的可解释性。GDCN 通过提出的Gated Cross Network (GCN) 对explicit feature interactions 进行建模，然后与DNN 集成以学习implicit feature interactions 。GCN 由两个核心组件组成：feature crossing 和information gate。feature crossing 组件在bounded degree 内捕获显式的交互，而information gate 则在每个cross order 上选择性地放大重要性高的important cross features 并减轻不重要特征的影响。此外，考虑到field 各自的重要性，FDO 方法可以为每个field 分配压缩的和独立的维度。

3. 贡献：

   • 我们引入了一种新方法GDCN ，通过GCN 和DNN 学习显式的和隐式的feature interactions 。GCN 设计了一个information gate 来动态地过滤next-order cross features 并有效地控制信息流。与现有方法相比，GDCN 在捕获更深层次的高阶交互方面表现出更高的性能和稳定性。

   • 我们开发了FDO 方法，为每个field 分配压缩的维度，考虑到每个field 固有的重要性。通过使用FDO，GCN 仅以原始模型参数的23% 实现了可比性能，并且以更小的模型大小、以及更快的训练速度超越了现有的SOTA 模型。

   • 综合实验表明GDCN 在五个数据集上具有很高的有效性和泛化能力。此外，我们的方法在model level 和instance level 提供了出色的可解释性，增强了我们对模型预测的理解。

   论文其实创新点不多也不大，更多的是工程上的工作。而且创新点之间（GCN 和 FDO ）没啥关系，强行拼凑一起得到一篇论文。

1.1 GDCN

1. 受DCN-V2 的启发，我们开发了GDCN ，它由embedding layer 、gated cross network (GCN) 和deep network (DNN) 组成。

   • embedding layer 将高维稀疏的输入转换为低维稠密的representations 。

   • GCN 旨在捕获显式的feature interactions ，并使用information gate 来识别重要的交叉特征。

   • 然后，DNN 被集成进来从而建模隐式的feature crosses 。

   本质上，GDCN 是DCN-V2 的泛化，继承了DCN-V2 出色的表达能力，并具有简单而优雅的公式，易于部署。然而，GDCN 通过采用information gates 从而引入了一个关键的区别，它在每个阶次中自适应地过滤交叉特征，而不是统一聚合所有特征。这使GDCN 能够真正利用deeper 的高阶cross-information ，而不会出现性能下降，并为GDCN 赋予了针对每个实例的动态可解释性。GDCN 的架构如Figure 1 所示，展示了结合GCN 和DNN 网络的两种结构：(a) GDCN-S and (b) GDCN-P 。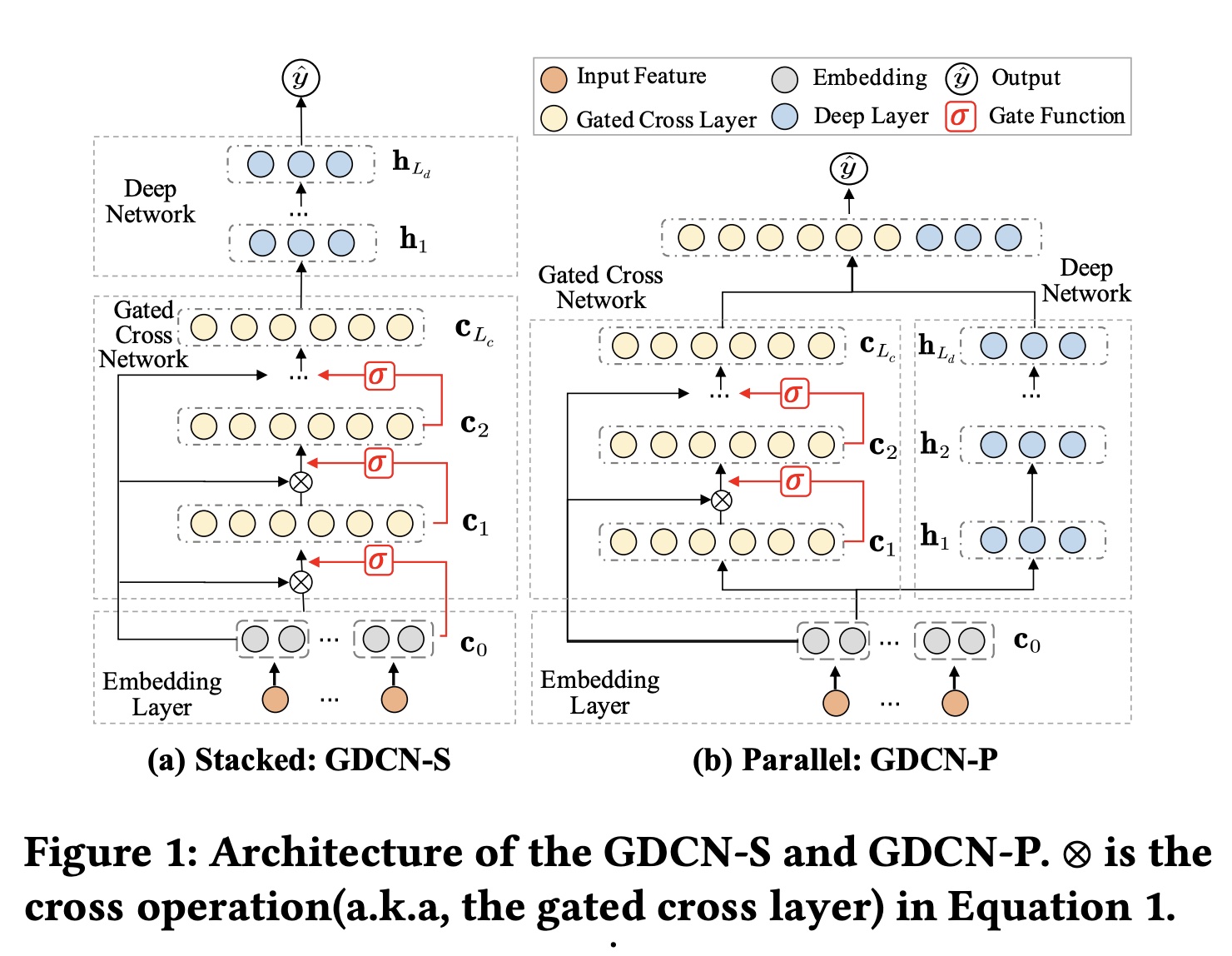

   

2. Embedding Layer：输入实例通常是multi-field tabular data records ，其中包含 $F$$F$ 个不同fields 和 $T$$T$ 个特征。每个实例都由一个field-aware one-hot vector 来表示。embedding layer 将稀疏的高维特征转换为稠密的低维embedding matrix $\mathbf{E}=[{\overrightarrow{\mathbf{e}}}_1;\cdots ;{\overrightarrow{\mathbf{e}}}_F]$$\mathbf E = \left[\mathbf{\vec e}_1;\cdots;\mathbf{\vec e}_F\right]$。大多数CTR 模型要求embedding 维度相同，从而匹配特定的interaction 操作。然而，GDCN 允许任意embedding 维度，并且embedding layer 的输出以向量拼接来表示：${\overrightarrow{\mathbf{c}}}_0=[{\overrightarrow{\mathbf{e}}}_1||\cdots ||{\overrightarrow{\mathbf{e}}}_F]\in {\mathbb{R}}^D$$\mathbf{\vec c}_0 = \left[\mathbf{\vec e}_1||\cdots||\mathbf{\vec e}_F\right]\in \mathbb R^D$ ，$D$$D$ 为拼接后的维度。

3. Gated Cross Network (GCN)：作为GDCN 的核心结构，GCN 旨在通过information gate 来建模显式的有界的feature crosses 。GCN 的第 $(l+1)$$(l+1)$ 个gated cross layer 表示为：

   $${\overrightarrow{\mathbf{c}}}_{l+1}=\underset{\text{Feature Crossing}}{\underbrace{{\overrightarrow{\mathbf{c}}}_0\odot ({\mathbf{W}}_l^{(c)}{\overrightarrow{\mathbf{c}}}_l+{\overrightarrow{\mathbf{b}}}_l)}}\odot \underset{\text{Information Gate}}{\underbrace{\sigma \left({\mathbf{W}}_l^{(g)}{\overrightarrow{\mathbf{c}}}_l\right)}}+{\overrightarrow{\mathbf{c}}}_l$$

   其中：

   • ${\overrightarrow{\mathbf{c}}}_0$$\mathbf{\vec c}_0$ 为来自embedding layer 的base input，其中包含一阶特征。

   • ${\overrightarrow{\mathbf{c}}}_l\in {\mathbb{R}}^D$$\mathbf{\vec c}_l\in \mathbb R^{D}$ 是是来自前一个gated cross layer （即，第 $l$$l$ 个gated cross layer ）的输出特征，用作当前第 $(l+1)$$(l+1)$ 个gated cross layer 的输入。

   • ${\overrightarrow{\mathbf{c}}}_{l+1}\in {\mathbb{R}}^D$$\mathbf{\vec c}_{l+1}\in \mathbb R^{D}$ 是当前第 $(l+1)$$(l+1)$ 个gated cross layer 的输出。

   • ${\mathbf{W}}_l^{(c)},{\mathbf{W}}_l^{(g)}\in {\mathbb{R}}^{D\times D}$$\mathbf W_l^{(c)}, \mathbf W_l^{(g)}\in \mathbb R^{D\times D}$ 为可学习的权重矩阵，${\overrightarrow{\mathbf{b}}}_l\in {\mathbb{R}}^D$$\mathbf{\vec b}_l\in \mathbb R^D$ 为可学习的偏置向量。

   • $\sigma (\cdot )$$\sigma(\cdot)$ 为sigmoid 函数，$\odot$$\odot$ 为逐元素乘积。

   Figure 2 可视化了gated cross layer 的过程。

   下图中的 $\times$$\times$ 实际上是矩阵乘法。

   

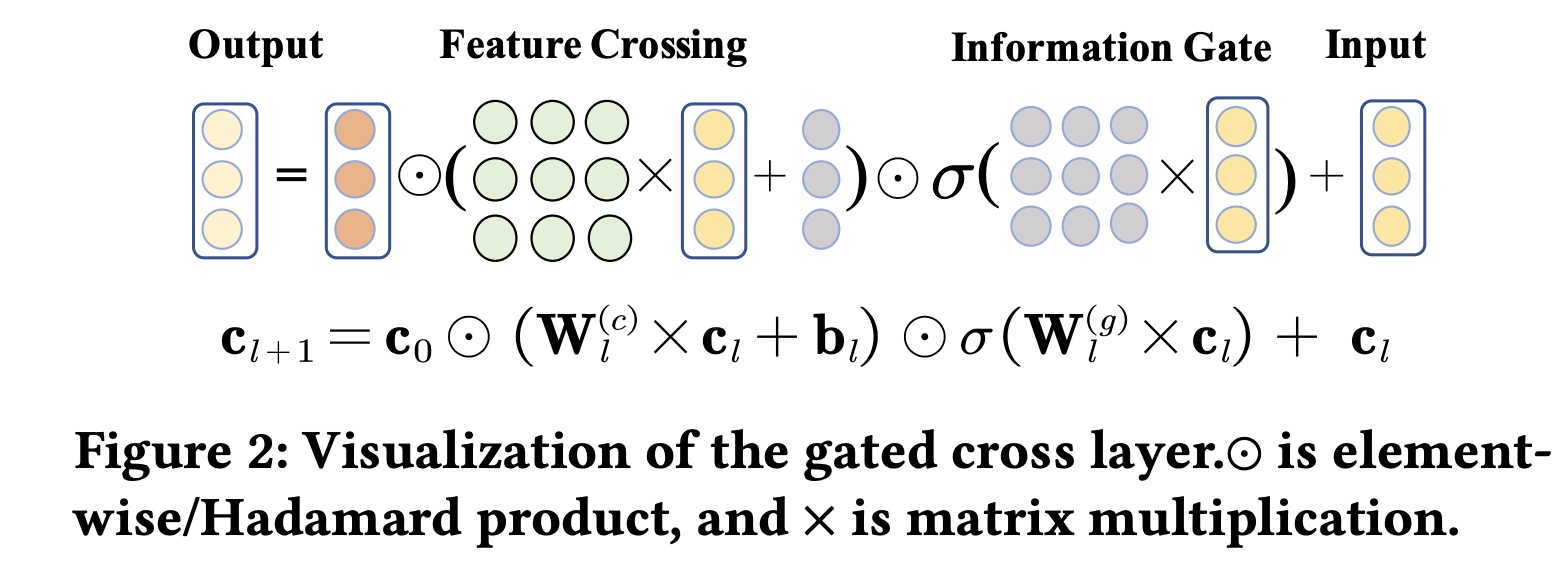
   在每个gated cross layer 中，都有两个核心组件：feature crossing 和information gate ，如公式和Figure 2 所示。

   • feature crossing 组件以bit-level 计算一阶特征 ${\overrightarrow{\mathbf{c}}}_0$$\mathbf{\vec c}_0$ 和 $l$$l$ 阶特征 ${\overrightarrow{\mathbf{c}}}_l$$\mathbf{\vec c}_l$之间的交互。然后，它输出下一个多项式阶次的交互，其中包含所有 $(l+1)$$(l+1)$ 阶交叉特征。矩阵 ${\mathbf{W}}_l^{(c)}$$\mathbf W_l^{(c)}$ 称为交叉矩阵（cross matrix ），表示第 $l$$l$ 阶中各个field 之间的固有重要性。

     但是，并非所有的 $(l+1)$$(l+1)$ 阶特征都对预测产生positive 影响。随着cross depth 的增加，交叉特征呈现指数级增长，这会引入交叉噪声并可能导致性能不佳。

   • 为了解决这个问题，我们引入了information gate 组件。作为soft gate ，它自适应地学习第 $(l+1)$$(l+1)$ 阶特征的重要性。通过将sigmoid 函数 $\sigma (\cdot )$$\sigma(\cdot)$ 应用于 $\left({\mathbf{W}}_l^{(g)}{\overrightarrow{\mathbf{c}}}_l\right)$$\left(\mathbf W_l^{(g)}\mathbf{\vec c}_l\right)$，可获得gate values 。然后将它们逐元素乘以feature crossing 的结果。此过程放大了重要特征，并减轻了不重要特征的影响。随着cross layers 数量的增加，每个cross layer 的information gate 都会过滤下一阶次的交叉特征并有效控制信息流。

   最后，通过将输入 ${\overrightarrow{\mathbf{c}}}_l$$\mathbf{\vec c}_l$ 与feature crossing and information gate 的结果相加，生成最终的output cross vector ${\overrightarrow{\mathbf{c}}}_{l+1}$$\mathbf{\vec c}_{l+1}$，从而包含从第0 阶到第 $(l+1)$$(l+1)$ 阶的所有特征交互。

   事实上，GCN 是 DCN 的变体，区别在与 GCN 多了一个 Information Gate 而已。那么，是否有更好的 Information Gate？比如，直接用 ${\overrightarrow{\mathbf{c}}}_0$$\mathbf{\vec c}_0$ 作为 information gate 的输入？

4. Deep Neural Network (DNN)：DNN 的目标是建模隐式feature interactions。DNN 的每个deep layer 表示为：

   $${\overrightarrow{\mathbf{h}}}_{l+1}=f({\mathbf{W}}_l{\overrightarrow{\mathbf{h}}}_l+{\overrightarrow{\mathbf{b}}}_l)$$

   其中：

   • ${\mathbf{W}}_l\in {\mathbb{R}}^{n_{l+1}\times n_l},{\overrightarrow{\mathbf{b}}}_l\in {\mathbb{R}}^{n_{l+1}}$$\mathbf W_l \in \mathbb R^{n_{l+1}\times n_l}, \mathbf{\vec b}_l\in \mathbb R^{n_{l+1}}$ 为第 $l$$l$ 个deep layer 中可学习的权重矩阵和偏置向量。

   • ${\overrightarrow{\mathbf{h}}}_l\in {\mathbb{R}}^{n_l},{\overrightarrow{\mathbf{h}}}_{l+1}\in {\mathbb{R}}^{n_{l+1}}$$\mathbf{\vec h}_l\in \mathbb R^{n_l}, \mathbf{\vec h}_{l+1}\in \mathbb R^{n_{l+1}}$ 为第 $l$$l$ 个deep layer 的input 和output，$n_l,n_{l+1}$$n_l,n_{l+1}$ 分别为对应的维度。

   • $f(\cdot )$$f(\cdot )$ 为激活函数，通常为ReLU 。

5. 整合GCN 和DNN：现有的研究主要采用两种结构来整合显式的和隐式的交互信息：堆叠和并行。因此，我们也以两种方式将GCN 和DNN结合起来，得到了两个版本的GDCN。

   • Figure 1(a) 展示了堆叠结构：GDCN-S 。

     • embedding 向量 ${\overrightarrow{\mathbf{c}}}_0$$\mathbf{\vec c}_0$ 被馈入到GCN 并输出 ${\overrightarrow{\mathbf{c}}}_{L_c}$$\mathbf{\vec c}_{L_c}$。

     • 然后 ${\overrightarrow{\mathbf{c}}}_{L_c}$$\mathbf{\vec c}_{L_c}$ 馈入DNN 从而生成最终的交叉向量 ${\overrightarrow{\mathbf{c}}}_{\text{final}}={\overrightarrow{\mathbf{h}}}_{L_d}$$\mathbf{\vec c}_\text{final} = \mathbf{\vec h}_{L_d}$。

     $L_c$$L_c$ 和 $L_d$$L_d$ 分别是gated cross layer and deep network 的深度。

   • Figure 1(b) 展示了并行结构：GDCN-P 。

     • embedding 向量 ${\overrightarrow{\mathbf{c}}}_0$$\mathbf{\vec c}_0$ 被并行地馈入GCN 和DNN 中。

     • GCN 和DNN 的输出（即 ${\overrightarrow{\mathbf{c}}}_{L_c}$$\mathbf{\vec c}_{L_c}$ 和 ${\overrightarrow{\mathbf{h}}}_{L_d}$$\mathbf{\vec h}_{L_d}$ ）被拼接起来以获得最终的交叉向量 ${\overrightarrow{\mathbf{c}}}_{\text{final }}=[{\overrightarrow{\mathbf{c}}}_{L_c}||{\overrightarrow{\mathbf{h}}}_{L_d}]$$\mathbf{\vec c}_\text{final } = \left[\mathbf{\vec c}_{L_c} ||\mathbf{\vec h}_{L_d}\right]$。

6. 训练和预测：最后，我们通过标准的逻辑回归函数计算预测点击率：

   $${\hat{y}}_i=\sigma \left({\overrightarrow{\mathbf{w}}}_{\text{logit}}^{\mathrm{\top }}{\overrightarrow{\mathbf{c}}}_{\text{final}}\right)$$

   其中：

   • ${\overrightarrow{\mathbf{w}}}_{\text{logit}}$$\mathbf{\vec w}_\text{logit}$ 是待学习的权重向量。

   • $\sigma (z)=1/(1+\exp (-z))$$\sigma(z) = 1/(1 + \exp(-z))$ 为sigmoid 函数。

   损失函数是广泛使用的二元交叉熵损失（又名LogLoss）：

   $${\mathcal{L}}_{\text{ctr}}=-\frac{1}{N}\sum _{i=1}^N(y_i\log \left({\hat{y}}_i\right)+(1-y_i)\log (1-{\hat{y}}_i))$$

   其中：${\hat{y}}_i$$\hat y_i$ 和 $y_i$$y_i$ 分别是预测点击率和真实点击率；$N$$N$ 是所有训练实例的数量。

7. 与DCN-V2 的关系：GDCN是DCN-V2的推广。当省略information gate 或所有gate values 都设置为1时，GDCN会退回到DCN-V2。在DCN-V2中，cross layer（即CN-V2）平等对待所有交叉特征并直接将它们聚合到下一个阶次，而未考虑不同交叉特征的不同重要性。然而，GDCN引入了GCN，在每个gated cross layer 中都包含一个information gate 。这个information gate 自适应地学习所有交叉特征的bit-wise gate values ，从而实现对每个交叉特征的重要性的细粒度控制。值得注意的是，GDCN和DCN-V2 都能够建模bit-wise and vector-wise 特征交叉，如DCN-V2 中所示。

   虽然GDCN和DCN-V2都使用了门控机制，但它们的目的和设计原理不同。

   • DCN-V2引入了MMoE的思想，将cross matrix 分解为多个较小的子空间或“专家”。然后，门控函数将这些专家组合在一起。这种方法主要减少了cross matrices 中的non-embedding 参数，同时保持了性能。

   • 不同的是，GDCN 利用门控机制自适应地选择重要的交叉特征，真正利用deeper 的交叉特征，而不会降低性能。它提供了动态的instance-based 的可解释性，可以更好地理解和分析模型的决策过程。

   为了进一步提高GDCN 的cost-efficiency ，接下来提出了一种field-level 维度优化方法，以直接减少embedding 参数。

1.2 FDO

1. embedding 维度通常决定了编码信息的能力。然而，为所有field 分配相同的维度会忽略不同field 的信息容量。例如，“性别” 和“item id ” 等field 中的特征的数量范围从 $O(2)$$O(2)$ 到 $O({10}^6)$$O(10^6)$。DCN-V2和DCN 采用经验公式根据每个field 的特征的数量，为每个field 分配独立的维度，即 $(\text{feature number}{)}^{0.25}$$(\text{feature number})^{0.25}$ 。这是一种先验的方法，但忽略了每个field 的真正重要性。 受FmFM 的启发，我们使用后验的 Field-level Dimension Optimization (FDO)方法，该方法根据每个field 在特定数据集中的固有重要性来学习其独立的维度。

   • 首先，我们训练一个完整模型，采用固定的field 维度为16 ，正如先前的研究所建议的那样。此过程使我们能够为每个field 生成一个informative embedding table 。

   • 接下来，我们使用PCA 为每个field 的embedding table 计算一组奇异值，按奇异值的幅值（magnitude）降序排列。通过评估信息利用率（即information ratio ），我们可以通过识别对整体information summation 贡献最大的 $\arg \underset{k}{min}$$\arg\min_k$ 个奇异值来确定最佳维度。此步骤使我们能够为每个field 选择合适的压缩维度。

   • 最后，我们使用上一步中学到的field 维度训练一个新模型。

   实际上，我们只需要基于full model 学习一次一组field dimensions ，然后在后续模型refresh 时重复使用它。

   Table 1 列出了具有80% 和95% 的 information ratio 时，每个field 的优化后的维度。

   • 当保留95% 比率时，field 维度范围为2 到15 。

   • 降低 information ratio 会导致每个field 的维度减少。

   • 具有大量特征的field 有时需要更高的维度，如在fields {#23, #24} 中观察到的那样。然而，情况并非总是如此；例如，fields {#16, #25} 表现出更小的维度。在实验部分中，我们提供了实验证据，表明field 的维度与其在预测过程中的重要性密切相关，而不是其特征数量

   • 此外，通过保留超过80% 的information ratio ，我们可以获得更轻的GCN 模型，其性能略优于具有完整embedding 维度的GCN 模型，并超过其他SOTA 模型。

   我们还对FDO 进行了更全面的分析，以了解field 维度与其固有重要性之间的联系。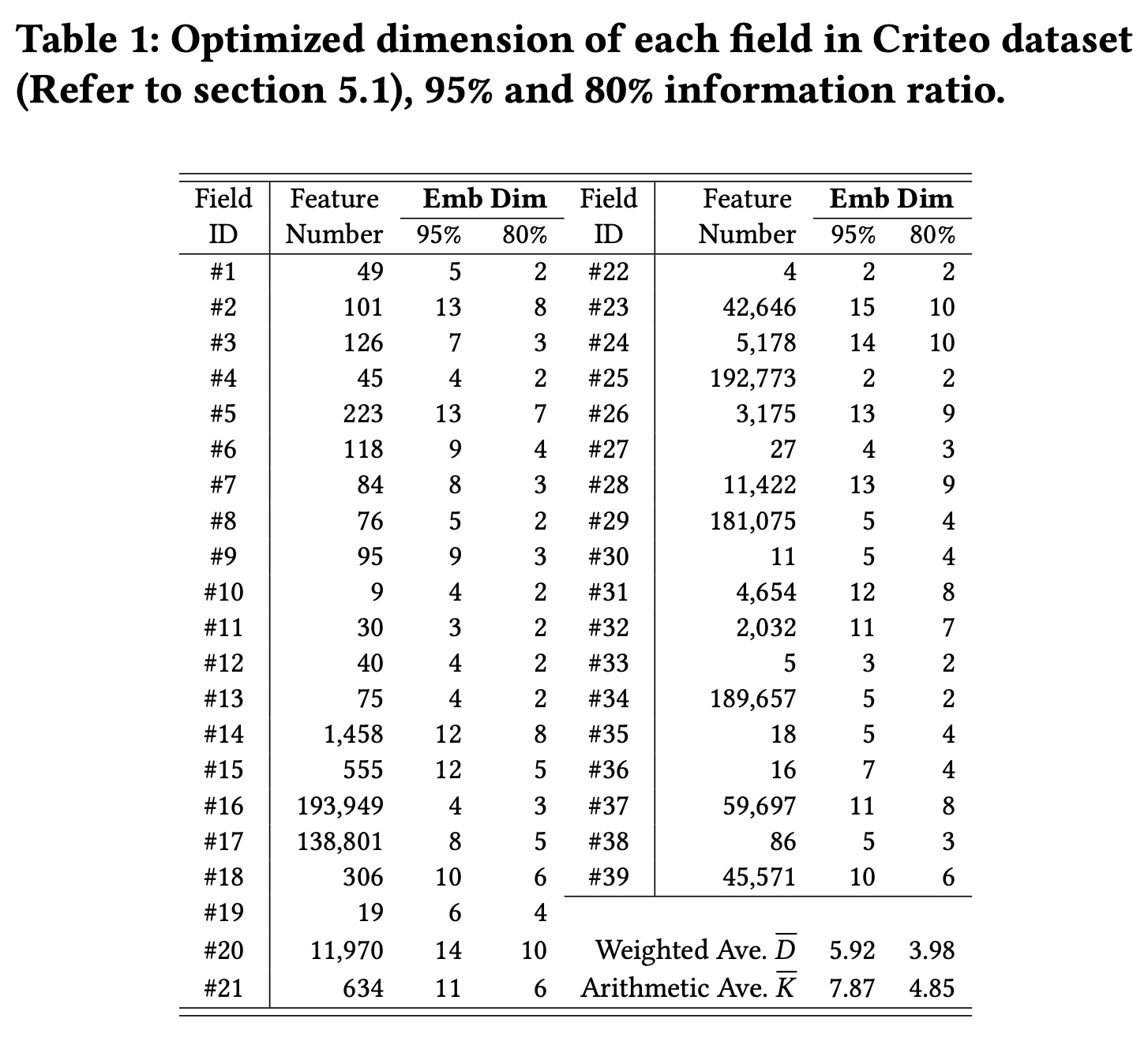

   

2. 参数分析：定义：

   • $\mathbb{E}=[{\mathbf{E}}_1,{\mathbf{E}}_2,\cdots ,{\mathbf{E}}_F]$$\mathbb E = \left[\mathbf E_1, \mathbf E_2, \cdots, \mathbf E_F\right]$ 为所有特征的embedding ； ${\mathbf{E}}_f$$\mathbf E_f$ 为feature representations 子集，对应于第 $f$$f$ 个field ，$1\le f\le F$$1\le f \le F$ 。

   • 第 $f$$f$ 个field 中的特征的数量记作 $|{\mathbf{E}}_f|$$|\mathbf E_f|$ ，数据集中的特征的总数量为 $T=\sum _{f=1}^F|{\mathbf{E}}_f|$$T = \sum_{f=1}^F |\mathbf E_f|$ 。

   • 类似地，令 $\mathbf{d}=[d_1,d_2,\cdots ,d_F]$$\mathbf d = [d_1,d_2,\cdots,d_F]$ 表示每个field 的embedding 维度，其中 $d_f$$d_f$ 为第 $f$$f$ 个field 的embedding 维度。

   对于一个输入的实例，算数平均的维度为 $\overline{K}=\left(\sum _{f=1}^F{d}_f\right)/F$$\bar K = \left(\sum_{f=1}^F d_f\right)/F$ ，embedding layer 的输出维度为 $D=F\overline{K}$$D= F\bar K$ 。考虑所有特征，加权平均维度记作 $\overline{D}=(\sum _{f=1}^F{d}_f|{\mathbf{E}}_f|)/T$$\bar D = \left(\sum_{f=1}^F d_f |\mathbf E_f|\right)/T$ 。embedding 参数的总量为 ${\mathcal{P}}_e=\sum _{f=1}^F{d}_f|{\mathbf{E}}_f|=T\overline{D}$$\mathcal P_e = \sum_{f=1}^F d_f|\mathbf E_f| = T\bar D$ 。在互联网规模数据集中，特征总数 $T$$T$ 的数量通常非常庞大。例如，在著名的Criteo 数据集中，原始特征数量超过30M ，稀疏度超过99.99% ，embedding 参数占据了模型参数的绝大部分。因此，$\overline{D}$$\bar D$ 决定了embedding 参数的数量，而 $\overline{K}$$\bar K$ 主要影响non-embedding 参数的数量，例如DCN-V2 和GCN 中的cross matrix ${\mathbf{W}}^{(c)}\in {\mathbb{R}}^{(F\overline{K})\times (F\overline{K})}$$\mathbf W^{(c)}\in \mathbb R^{(F\bar K)\times (F\bar K)}$。

   时间复杂度主要与 $\overline{K}$$\bar K$ 有关。

   通过采用FDO 方法，我们可以通过缩小某些field 的不必要维度来refine 特征维度，以减少冗余的embedding 参数。

   • 当使用固定维度16 时，embedding 参数为 $16T$$16T$ 。

   • 然而，在95% information ratio 的FDO 之后，embedding 参数减少到 $5.92T$$5.92T$，仅占原始embedding 参数的37% 。

   • 如果我们根据公式（即 $d_f=|{\mathbf{E}}_f{|}^{0.25}$$d_f = |\mathbf E_f|^{0.25}$）计算field 维度，加权平均维度 $\overline{D}$$\bar D$ 变为18.66 ，导致emebdding 参数为 $18.66T$$18.66T$，大于 $16T$$16T$ 。此公式为具有大量特征的field 分配了更大的维度，忽略了每个field 的特定重要性。相比之下，FDO 是一种后验方法，它基于从训练好的embedding table 中提取的特定信息来学习field-level 维度。

   随着field 维度的降低，算术平均维度 $\overline{K}$$\bar K$ 也相应降低（例如，从16 降至7.87 ）。这样，GCN 网络中的non-embedding 参数，即cross matrix ${\mathbf{W}}^{(c)}\in {\mathbb{R}}^{(F\overline{K})\times (F\overline{K})}$$\mathbf W^{(c)}\in \mathbb R^{(F\bar K)\times (F\bar K)}$ 和gate matrix ${\mathbf{W}}^{(g)}\in {\mathbb{R}}^{(F\overline{K})\times (F\overline{K})}$$\mathbf W^{(g)}\in \mathbb R^{(F\bar K)\times (F\bar K)}$ 也自然减少了。

1.3 实验

1. 数据集：Criteo、Avazu、Malware 、Frappe、ML-tag 。这些数据集的统计数据如Table 2 所示，详细描述可在给定的参考文献中找到。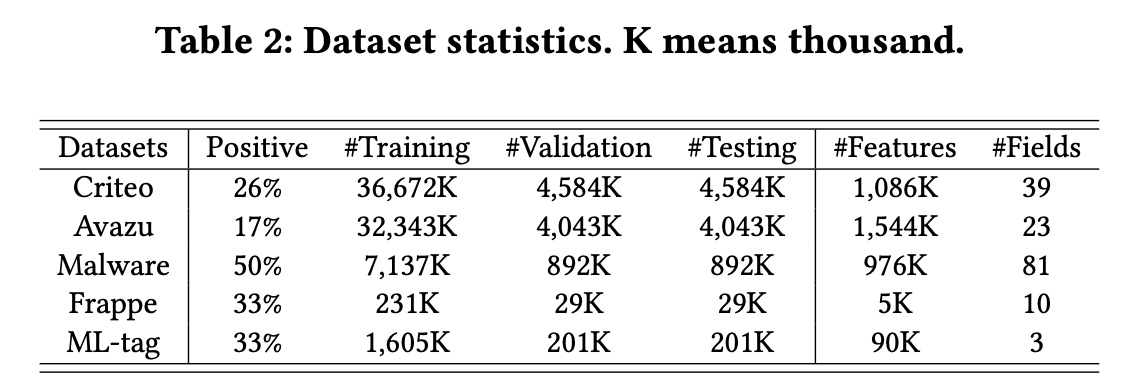

   

2. 数据预处理：

   • 首先，我们将每个数据集随机分成训练集（80%）、验证集（10%）和测试集（10% ）。

   • 其次，在Criteo 和Avazu中，我们删除某个field 中出现次数少于阈值的低频特征，并将其视为dummy feature "<unkonwn>" 。Criteo 和Avazu 的阈值分别设置为{10, 5} 。

   • 最后，在Criteo数据集中，我们通过将实数值 $z$$z$ 转换为：当 $z>2$$z\gt 2$ 时 $\lfloor {\log }_2(z)\rfloor$$\lfloor\log_2(z)\rfloor$ ；否则为1 。这是Criteo 竞赛的获胜者所采用的。

3. 评估指标：AUC、Logloss 。

4. baseline 方法：我们与四类代表性的方法进行了比较。

   • 一阶方法，例如LR 。

   • 建模二阶交叉特征的基于FM 的方法，包括FM、FwFM、DIFM和FmFM 。

   • 捕获高阶交叉特征的方法，包括CrossNet(CN)、CIN、AutoInt、AFN、CN-V2、IPNN、OPNN、FINT、FiBiNET 和SerMaskNet。

   • 代表性的集成/并行方法，包括WDL、DeepFM、DCN、xDeepFM、AutoInt+、AFN+、DCN-V2、NON、FED 和ParaMaskNet。

   我们没有展示某些方法的结果，例如CCPM、GBDT、FFM、HoFM、AFM、NFM，因为许多模型已经超越了它们。

5. 实现细节：

   • 我们使用Pytorch实现所有模型，并参考现有工作。

   • 我们使用Adam 优化器优化所有模型，默认学习率为0.001。我们在训练过程中使用Reduce-LR-On-Plateau scheduler ，当性能在连续3 epochs 停止改善时，将学习率降低10 倍。

   • 我们在验证集上应用patience = 5 的早停（early stopping），以避免过拟合。

   • batch size 设置为4096 。所有数据集的embedding 维度均为16 。

   • 根据先前的研究，我们对涉及DNN的模型采用相同的结构（即3层，400-400-400 ），以便进行公平比较。除非另有说明，所有激活函数均为ReLU ，dropout rate = 0.5 。

   • 对于我们提出的GCN、GDCN-S 和GDCN-P ，除非另有说明，默认的gated cross layer 数量为3 。

   • 对于其他baseline ，我们参考了两个benchmark 工作（即 BARS 和FuxiCTR ）及其原始文献来微调它们的超参数。

6. 显著性检验：为了确保公平比较，我们在单个GPU（NVIDIA TITAN V）上使用随机种子运行每种方法10次，并报告平均的测试性能。我们执行双尾t-test 来检测我们的方法与最佳baseline 方法之间的统计显着性。在所有实验中，与最佳baseline 相比的改进具有统计学意义（$p<0.01$$p<0.01$），在Table 3 和Table 4 中用 ★ 表示。

1.3.1 整体性能

注意，这里的结果是在没有应用 FDO 的情况下得出的。

1. 与堆叠式模型的比较：我们将GCN 和GDCN-S 与 stacked baseline 模型进行比较，包括一阶、二阶和高阶模型。整体性能总结在Table 3 中。我们有以下观察结果：

   • 首先，在大多数情况下，高阶模型优于一阶模型和二阶模型，证明了学习复杂的高阶feature interactions 的有效性。值得注意的是，OPNN、FiBiNet、FINT 和SerMaskNet 等模型表现更佳，它们使用一个stacked DNN 同时捕获显式的和隐式的特征交叉。这证实了对显式的和隐式的高阶feature interactions 进行建模背后的原理。

   • 其次，GCN 通过仅考虑显式的多项式feature interactions ，始终优于所有堆叠的baseline 模型。GCN是CN-V2的泛化，增加了一个information gate 来识别有意义的交叉特征。GCN 的性能验证了并非所有交叉特征都对最终预测有益，大量不相关的交互会引入不必要的噪音。通过自适应地re-weighting 每个阶次中的交叉特征，GCN 比CN-V2 实现了显著的性能提升。此外，它优于SerMaskNet ，平均 $\mathrm{\Delta }\text{AUC}$$\Delta \text{AUC}$ 提高0.14% ，平均 $\mathrm{\Delta }\text{LL}$$\Delta \text{LL}$ 改善了0.45% 。

   • 第三，GDCN-S 超越了所有堆叠的baseline 并实现最佳性能。在 GDCN-S 中，stacked DNN 进一步学习GCN 结构之上的隐式交互信息。因此，与其他堆叠式模型（例如OPNN、FINT和SerMaskNet）相比，GDCN-S优于GCN并实现更高的预测准确率。具体来说，与SerMaskNet相比，GDCN-S实现了平均0.28% （$\mathrm{\Delta }\text{AUC}$$\Delta \text{AUC}$ ）和2.70% （ $\mathrm{\Delta }\text{LL}$$\Delta \text{LL}$ ）的改善。

   

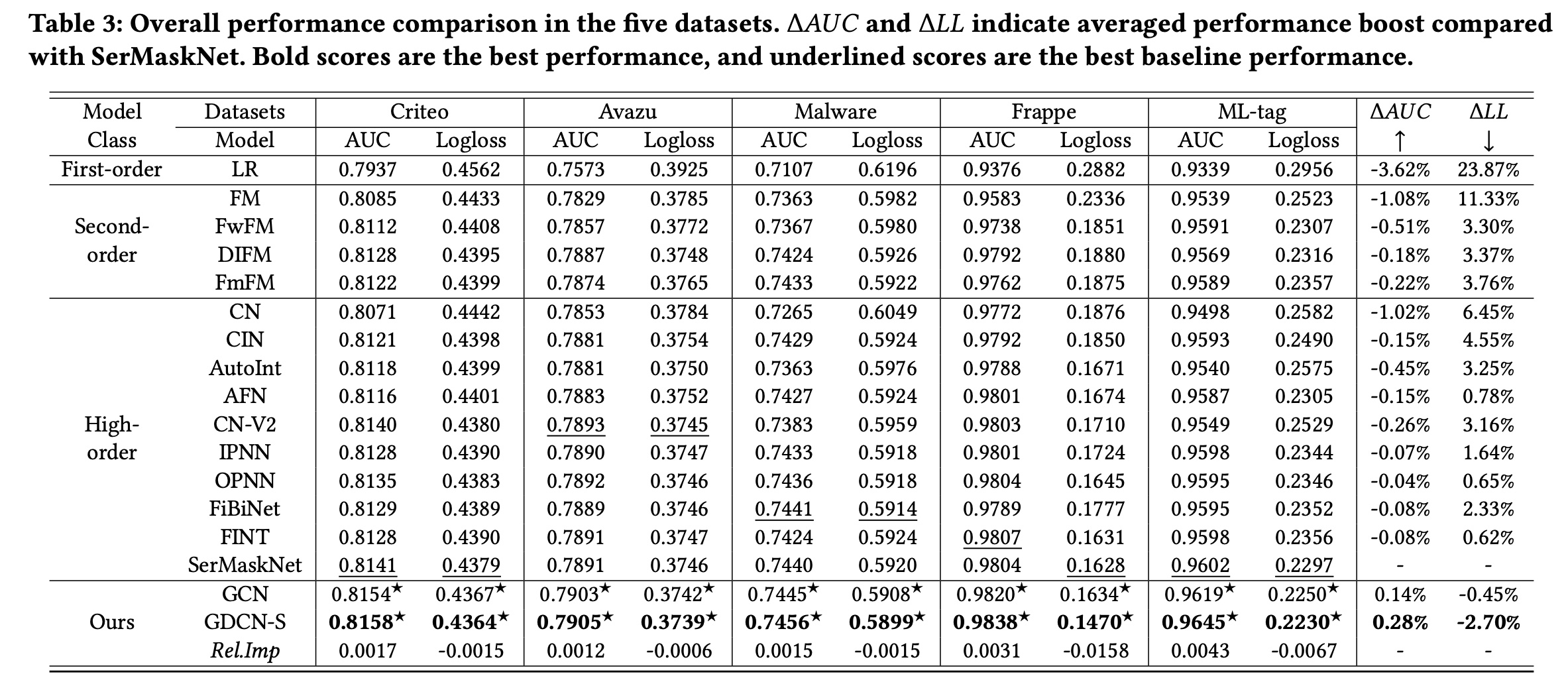
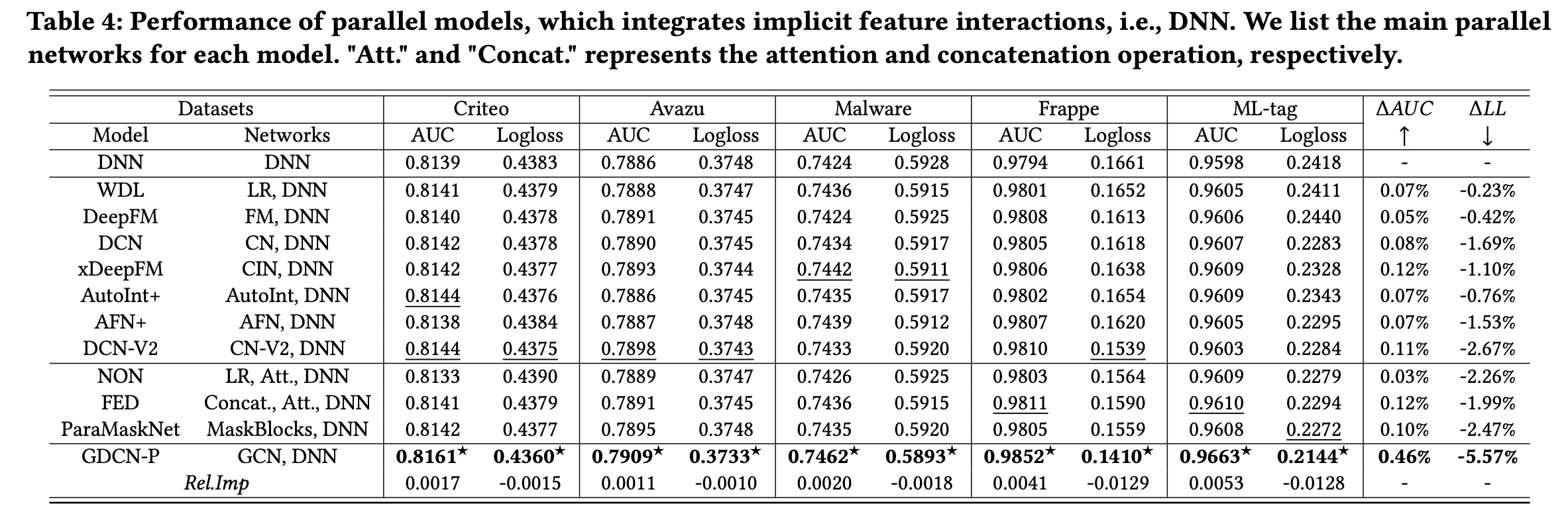
2. 与并行式模型的比较：Table 4 展示了SOTA 的ensemble/parallel 模型的性能。每种方法都包含并行网络，例如DeepFM 中的FM和DNN，以及DCN-V2 中的CN-V2和DNN。此外，我们将这些模型与常规的DNN 模型进行比较，并在此基础上计算 $\mathrm{\Delta }\text{AUC}$$\Delta \text{AUC}$ 和 $\mathrm{\Delta }\text{LL}$$\Delta \text{LL}$ 的平均改进。我们的观察结果如下：

   • 首先，整合隐式的和显式的feature interactions 可以增强预测能力。DNN 仅建模隐式的feature interactions ，而将DNN 与捕获显式feature interactions 的其他网络相结合得到的并行模型优于单个网络。值得注意的是，GCN 显示出最显著的平均性能改进，从 $\mathrm{\Delta }\text{AUC}$$\Delta \text{AUC}$ 和 $\mathrm{\Delta }\text{LL}$$\Delta \text{LL}$ 分别为0.46%和5.57%可以看出。这凸显了GCN 与其他basic operation 网络相比的卓越能力。

   • 其次，GDCN-P 的表现优于所有并行式模型和堆叠式模型。与Table 4 中的并行式模型相比，GDCN-P 实现了卓越的性能，超越了所有最佳baseline。此外，当考虑堆叠式模型并使用Table 3 中的SerMaskNet 作为benchmark 时，GDCN-P 实现了0.38%（ $\mathrm{\Delta }\text{AUC}$$\Delta \text{AUC}$ ）和4.26% （ $\mathrm{\Delta }\text{LL}$$\Delta \text{LL}$）的平均改进。

   

1.3.2 Deeper 高阶特征交叉

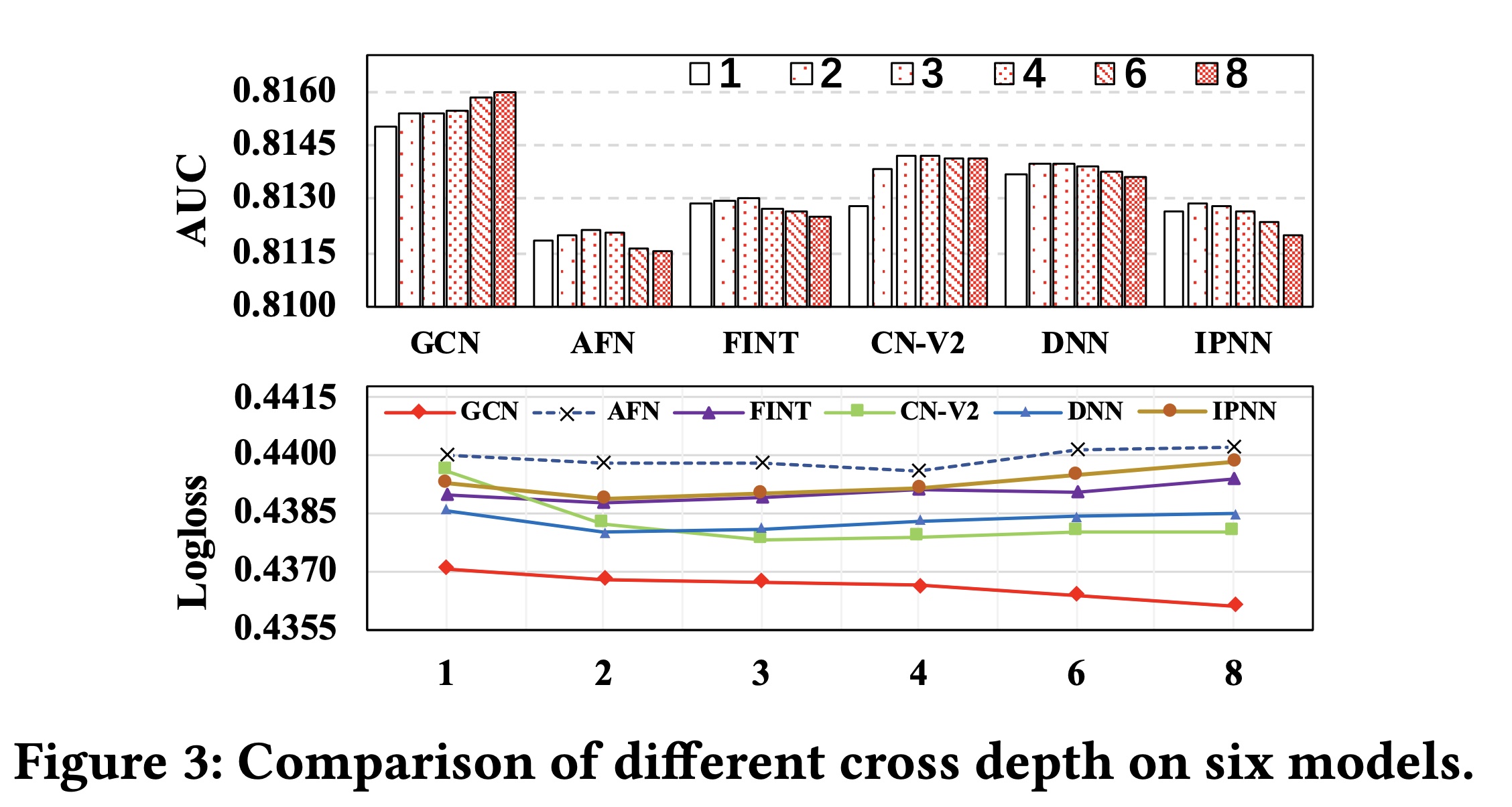
1. 通过改变cross depth将GCN 与其他模型进行比较：我们将GCN 与五个可以捕获高阶交互的代表性模型进行比较，即AFN、FINT、CN-V2、DNN 和IPNN。Figure 3 说明了在Criteo 数据集上随着cross depth的增加而出现的测试AUC 和Logloss 。

   • 随着交叉层的增加，五个被比较的模型的性能得到改善。然而，当cross depth 变得更深（例如，超过2、3 或4 个交叉层）时，它们的性能会显著下降。这些模型可以在功能上捕获更深的高阶显式和隐式的feature interactions ，但高阶的交叉特征也会引入不必要的噪声，这可能会导致过拟合并导致结果下降。在许多SOTA 工作中进行的cross depth 超参数分析中也观察到了这个问题。

   • 相反，随着交叉层数从1 增加到8，GCN的性能不断提高。具体来说，与CN-V2模型相比，GCN包含了一个information gate 。该information gate 使GCN能够对每个阶次识别有用的交叉特征，并仅积累最终预测所需的信息。因此，即使cross depth 变得更深，GCN 的表现始终优于CN-V2和其他模型，验证了information gate 设计的合理性。

   

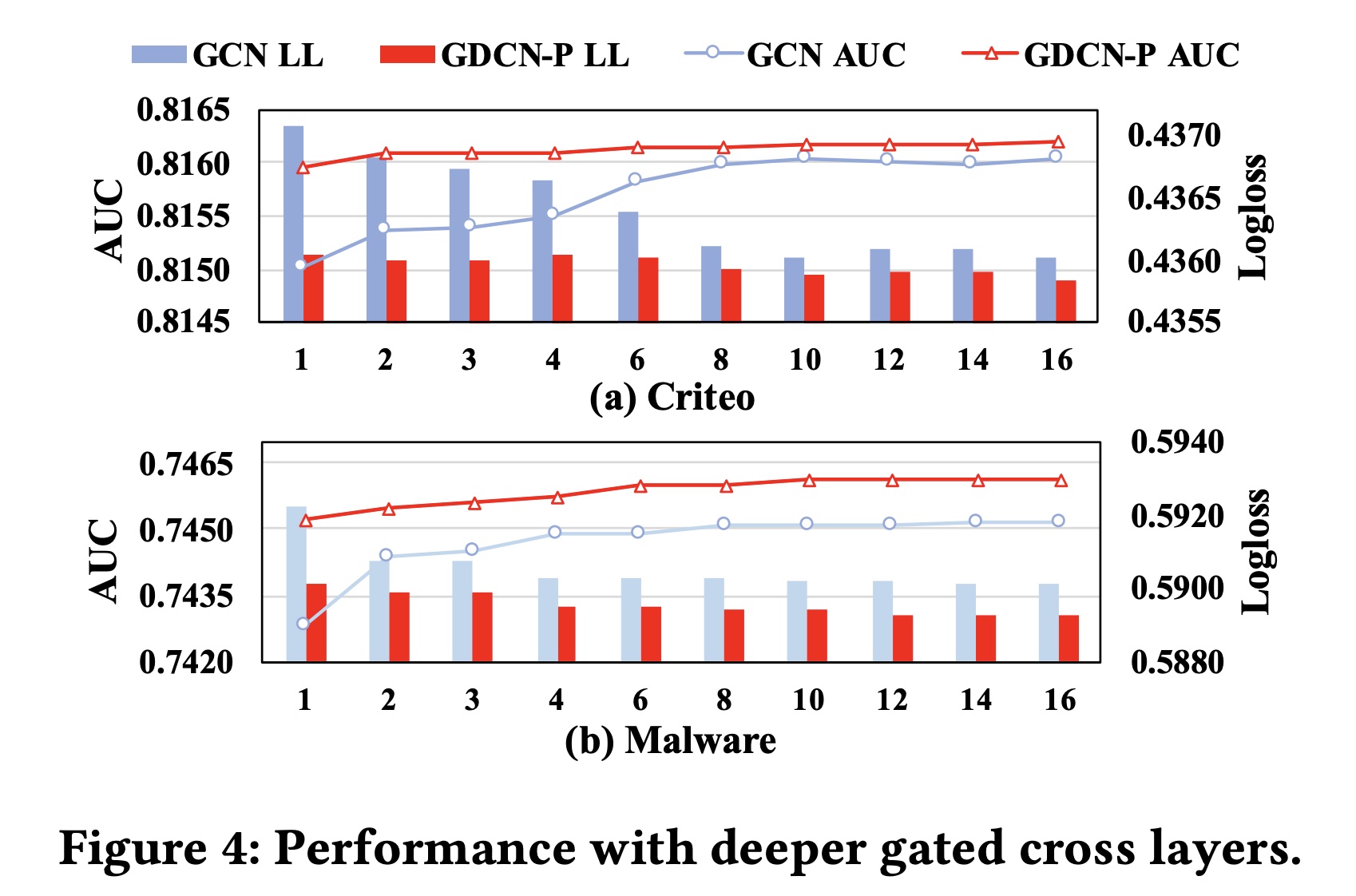
2. 具有更深gated cross layers 的GCN 和GDCN-P 的性能：在Criteo 和Malware 数据集上，我们进一步将GCN 和GDCN-P的cross depth 从1增加到16。值得注意的是，我们将GDCN-P 中的DNN深度固定在3，以防止DNN导致的过拟合。Figure 4 展示了实验结果。

   • 随着cross depth的增加，GCN和GDCN-P的性能都得到了改善，在GDCN-P 中观察到的趋势与GCN的趋势一致。

   • 在加入DNN组件后，GDCN-P 的表现始终优于GCN，这凸显了使用DNN捕获隐式feature interactions 的重要性。

   • 此外，DNN 使GDCN-P能够更早地获得最佳结果。具体来说，当深度超过8或10时，GCN的性能会达到稳定状态，而GDCN-P 的阈值为4或6。

   • 尽管GCN 和GDCN-P 可以选择有价值的交叉特征，但随着cross depth的增加，高阶交叉特征的有用性会急剧下降。这种现象符合人们的普遍直觉，即个人在做出决策（例如点击或购买item ）时通常不会同时受到太多特征的影响。

   • 值得注意的是，在cross depth超过稳定阈值后，我们的模型的性能保持稳定，而不是下降。

   

1.3.3 GCN 的可解释性

1. 可解释性对于理解specific predictions背后的原因、以及增强对预测结果的信心至关重要。GCN 从模型的和实例的角度提供静态的和动态的解释，有助于全面理解模型的决策过程。

2. 静态的model interpretability：在GCN 中，交叉矩阵 ${\mathbf{W}}^{(c)}$$\mathbf W^{(c)}$ 作为不同fields 之间交互的相对重要性的指标。如果每个实例由F 个fields 组成，每个field 具有相同的field size $d$$d$ ，则交叉矩阵可以按bit-wise 和block-wise 的方式来表示：

   $$\begin{array}{c}{\mathbf{W}}^{(c)}=\left[\begin{array}{ccc}{w}_{1,1}& \cdots & w_{1,Fd}\\ ⋮& \ddots & ⋮\\ w_{Fd,1}& \cdots & w_{Fd,Fd}\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{W}}_{1,1}& \cdots & {\mathbf{W}}_{1,F}\\ ⋮& \ddots & ⋮\\ {\mathbf{W}}_{F,1}& \cdots & {\mathbf{W}}_{F,F}\end{array}\right]\end{array}$$

   其中，每个分块矩阵 ${\mathbf{W}}_{i,j}\in {\mathbb{R}}^{d\times d}$$\mathbf W_{i,j}\in \mathbb R^{d\times d}$ 显示了第 $i$$i$ 个field 和第 $j$$j$ 个field 之间一阶交叉的重要性。当应用FDO 学习各个field 维度时，分块矩阵 ${\mathbf{W}}_{i,j}\in {\mathbb{R}}^{d_i\times d_j}$$\mathbf W_{i,j} \in \mathbb R^{d_i\times d_j}$ ，$d_i,d_j$$d_i, d_j$ 是第 $i$$i$ 个field 和第 $j$$j$ 个field 的不同维度。

   ${\mathbf{W}}_{l,i,j}^{(c)}$$\mathbf W^{(c)}_{l,i,j}$ 刻画的是第 $l+1$$l+1$ 阶的第 $i$$i$ 个 field 与第 $l$$l$ 阶的第 $j$$j$ 个 field 之间的一阶交叉的重要性。

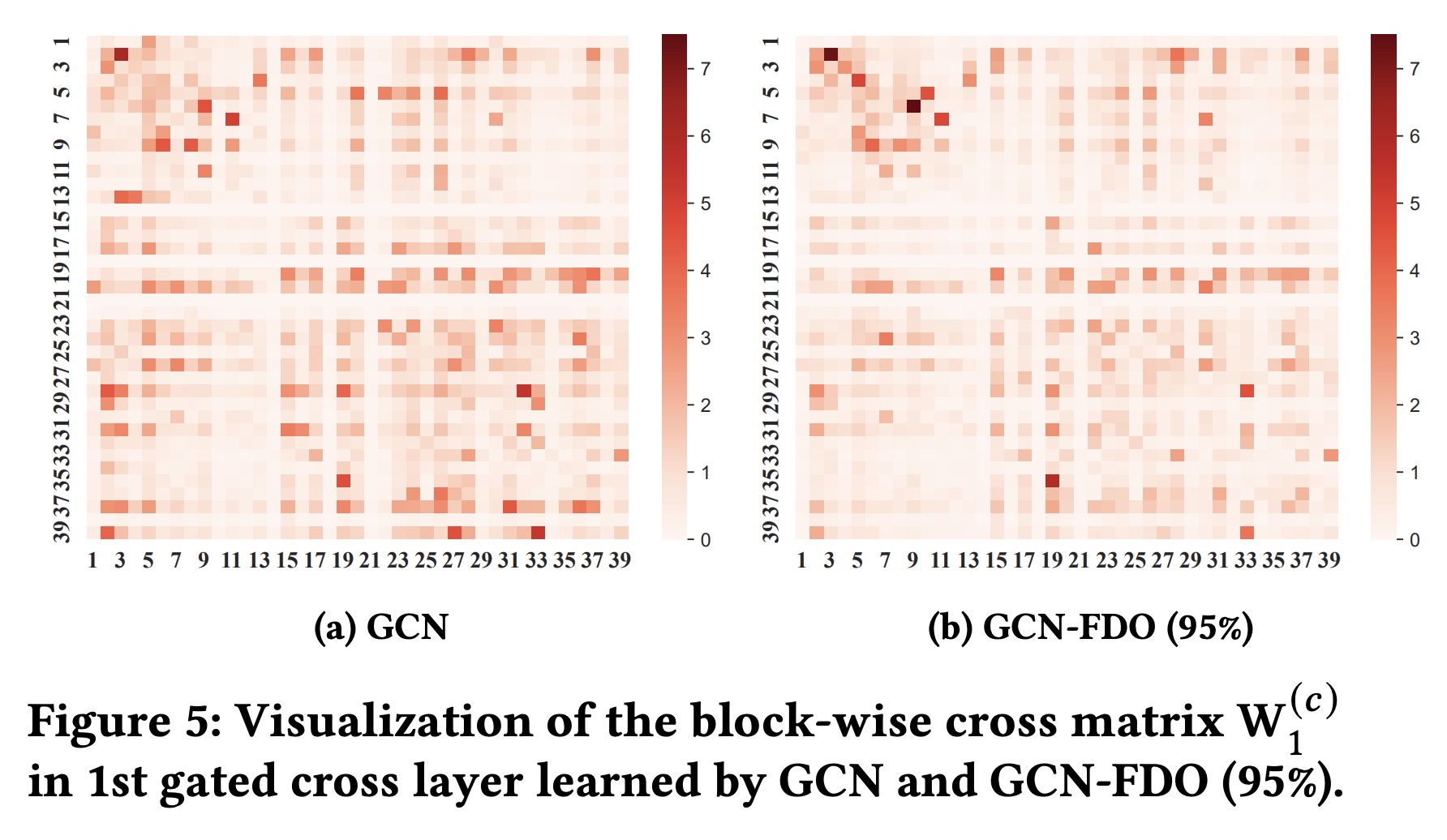
   此外，随着交叉层的增加，相应的交叉矩阵可以进一步表明多个field 之间的固有的relation importance 。

   • Figure 5(a) 展示了GCN在Criteo数据集上学到的第一阶交叉层的分块交叉矩阵 ${\mathbf{W}}_1^{(c)}$$\mathbf W_1^{(c)}$ 的热力图。与DCN-V2 类似，每个color box 代表相应分块矩阵 ${\mathbf{W}}_{i,j}$$\mathbf W_{i,j}$ 的Frobenius 范数，表示field cross 的重要性。红色越深，表示学到的交叉越强，例如<#3, #2> 和<#9, #6>。

   • 将FDO 方法应用于GCN时，GCN-FDO仍然能够捕获相似的交叉重要性，如Figure 5(b) 所示。两个矩阵之间的余弦相似度为0.89，表明在应用FDO之前和之后，在捕获固有field cross 重要性方面具有很强的一致性。

   

3. 动态的instance interpretability：基于模型的可解释性可以捕获不同field 之间的静态关系，但由于模型训练完成后交叉矩阵保持不变，因此存在局限性。然而，GCN 还通过information gate 学到的gate weights 提供动态可解释性，为每个input instance 提供bit-wise 的和field-wise 的解释。

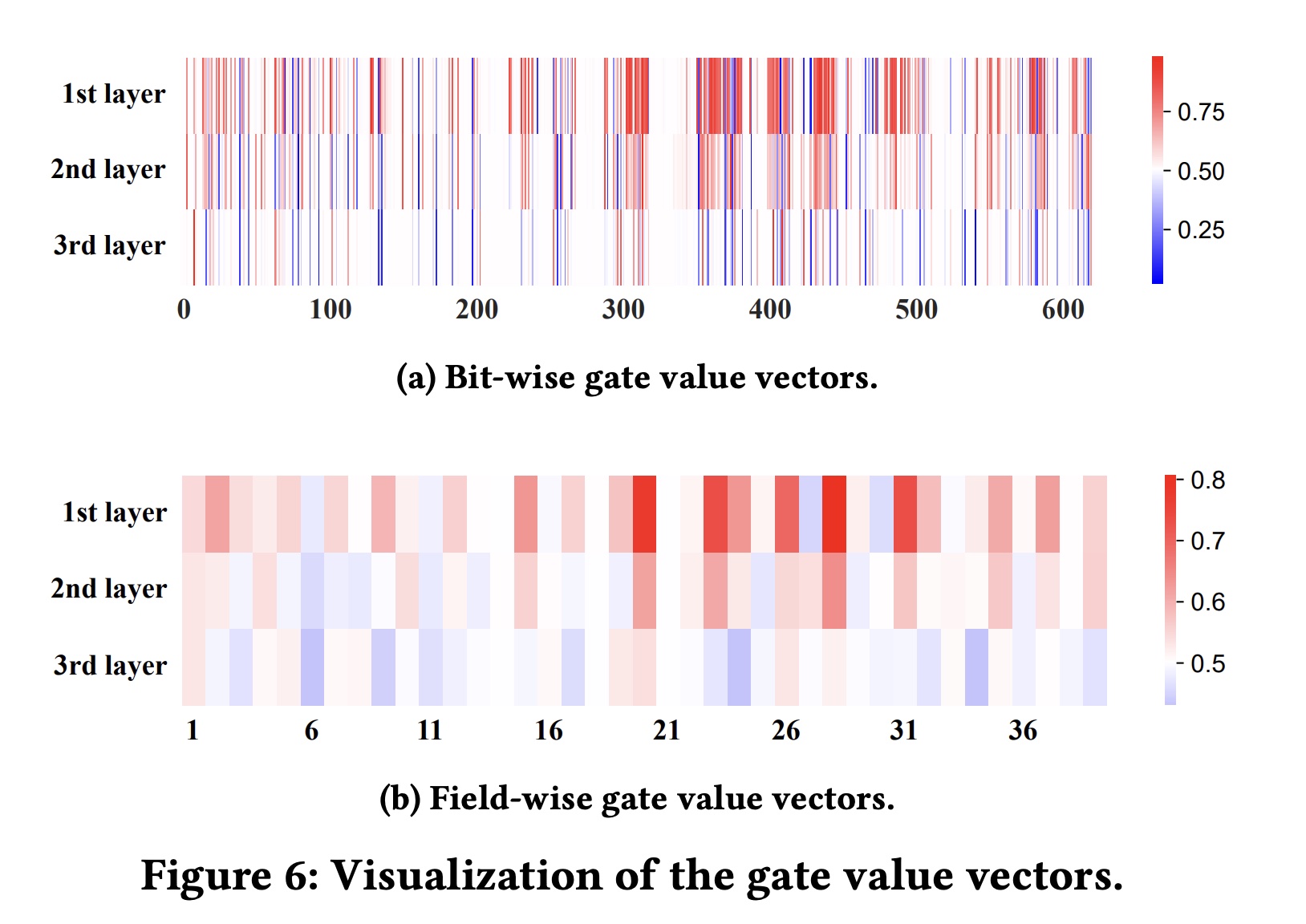
   我们从Criteo 数据集中随机选择两个实例来可视化学到的gate weights ，并检查从第一个到第三个gated cross layer 的gate values 。

   • Figure 6(a) 展示了bit-wise gate weight vectors ，每层的维度为 ${\mathbb{R}}^{1\times (39\ast 16)}$$\mathbb R^{1\times (39*16)}$，显示了每个bit-wise cross 的重要性。使用bit-wise gate vector ，我们通过对每个field 对应的16-bit values 取平均值来导出field-wise gate vectors 。

   • Figure 6(b) 显示了field-wise gate weight vectors （${\mathbb{R}}^{1\times 39}$$\mathbb R^{1\times 39}$），表示每个specific feature 的重要性。由于gated cross layer 中的gate weights 是使用sigmoid 函数计算的，因此red blocks （大于0.5 ）表示重要特征，而blue blocks （小于0.5 ）表示不重要特征。

   Figure 6(a) 和Figure 6(b) 揭示了bit-level 和field-level 的交叉特征的重要性，以及它们在每个实例的不同cross layers 中是如何变化的。

   • 通常，低阶特征交叉包含更重要的特征，而高阶特征交叉包含不太重要的特征。在第一层中，许多特征交叉被标识为重要的（红色块），而在第二和第三交叉层中，大多数交叉是中性的（白色块）或不重要的（蓝色块），尤其是在第三层。这符合我们的直觉：随着交叉层的增加，重要的交叉特征的数量显著减少，因此我们设计了information gate 来自适应地选择重要特征。相反，大多数模型在建模高阶交叉时无法选择有用的特征交叉，导致性能下降，如《Deeper 高阶特征交叉》 章节所证实的。

   • 此外，从Figure 6(b) 中，我们可以识别出重要的或不重要的特定特征，例如特征{#20, #23, #28} 很重要，而特征{#6, #11, #30} 不重要。我们还可以从input instance 中引用这些specific important features 的名称。一旦我们知道哪些特征有影响，我们就可以解释甚至干预有助于用户点击率的相关特征。

   

   最后，在Figure 7 中，我们记录并平均了M 个实例的field-level gate vectors ，表明每个field 的平均重要性，特别是在第一层。例如，field {#20, #23, #24} 非常重要，而field {#11, #27, #30} 相对较不重要。此外，Figure 7 从统计角度进一步验证了随着交叉层的增加，重要交叉特征的数量显著减少。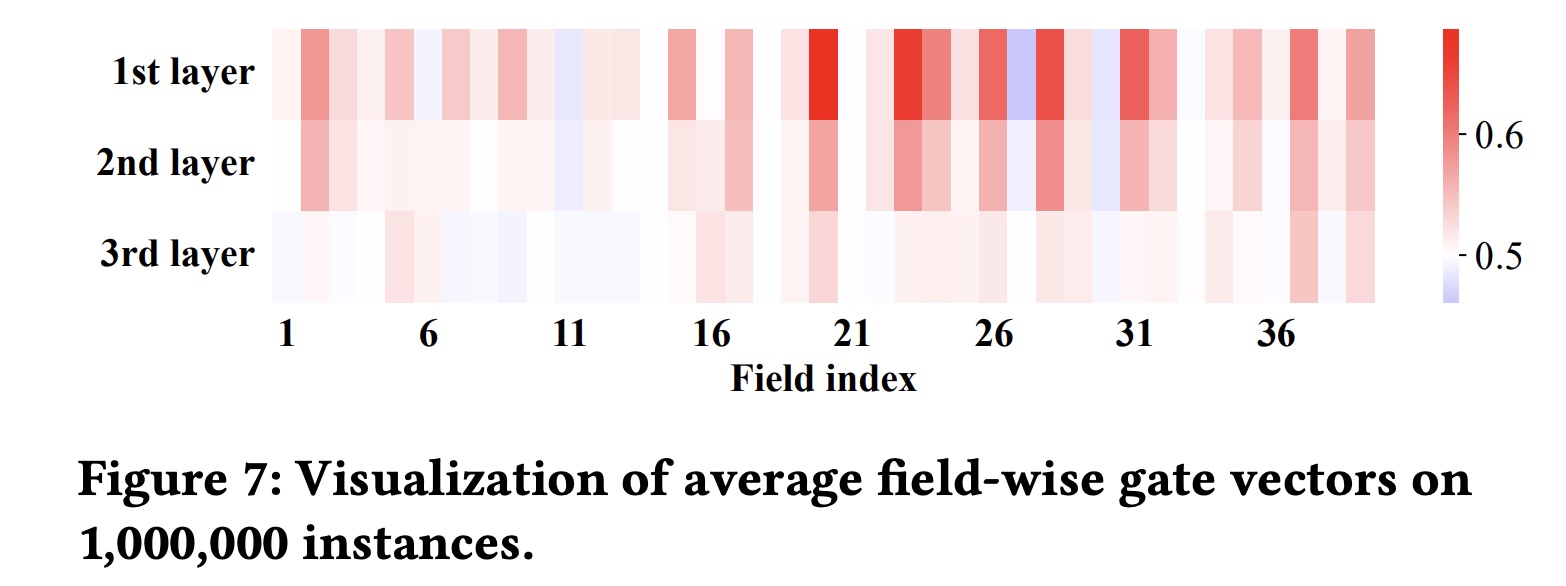

   

413.4 FDO 的综合分析

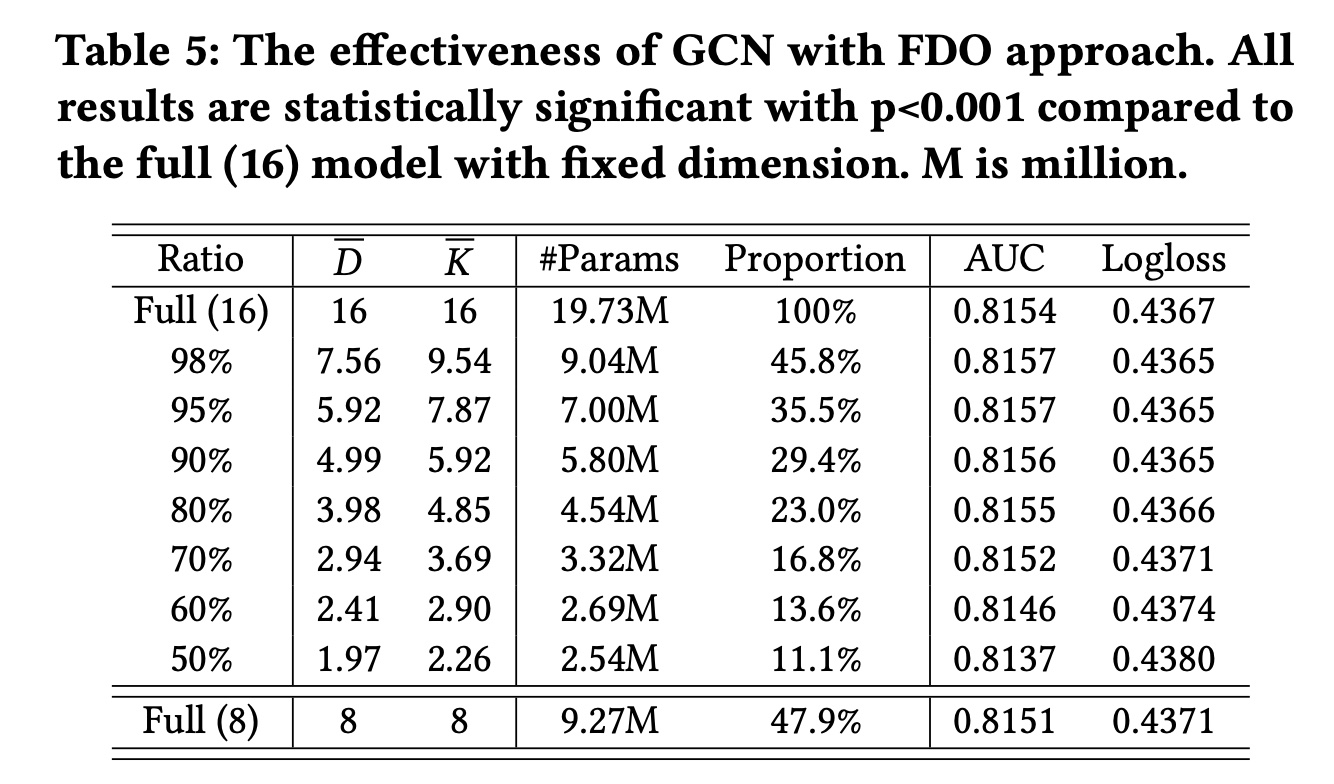
1. 效果分析：我们将FDO方法应用于GCN，并通过保持information ratio 从50% 到98%来评估其性能。Table 5 显示了结果，包括权重平均维度 $\overline{D}$$\bar D$ 、算术平均维度 $\overline{K}$$\bar K$ 和参数总数 (#Params)。

   • 当保持80% 的information ratio 时，我们只需要23%的参数，而模型的性能与完整模型相当。

   • 此外，当information ratio 在80% 到98%之间时，模型性能甚至比完整模型更好。这是因为FDO refine 了每个field 的特征维度，消除了非必要的维度信息并减少了交叉过程中的冗余。

   • 然而，当information ratio 较低（即低于80% ）时，较短的维度无法充分表示相应field 的特征，导致预测性能显著下降。

   • 最后，我们将整个模型的维度从16 减少到8，大约相当于95% 比率下的加权平均维度（7.56 ）。虽然它直接减少了模型的参数，但也导致了性能的下降。其他研究同样证实了减少embedding 大小的负面影响。相比之下，FDO 方法可以更直接地减少参数数量，同时实现相媲美的性能。

   

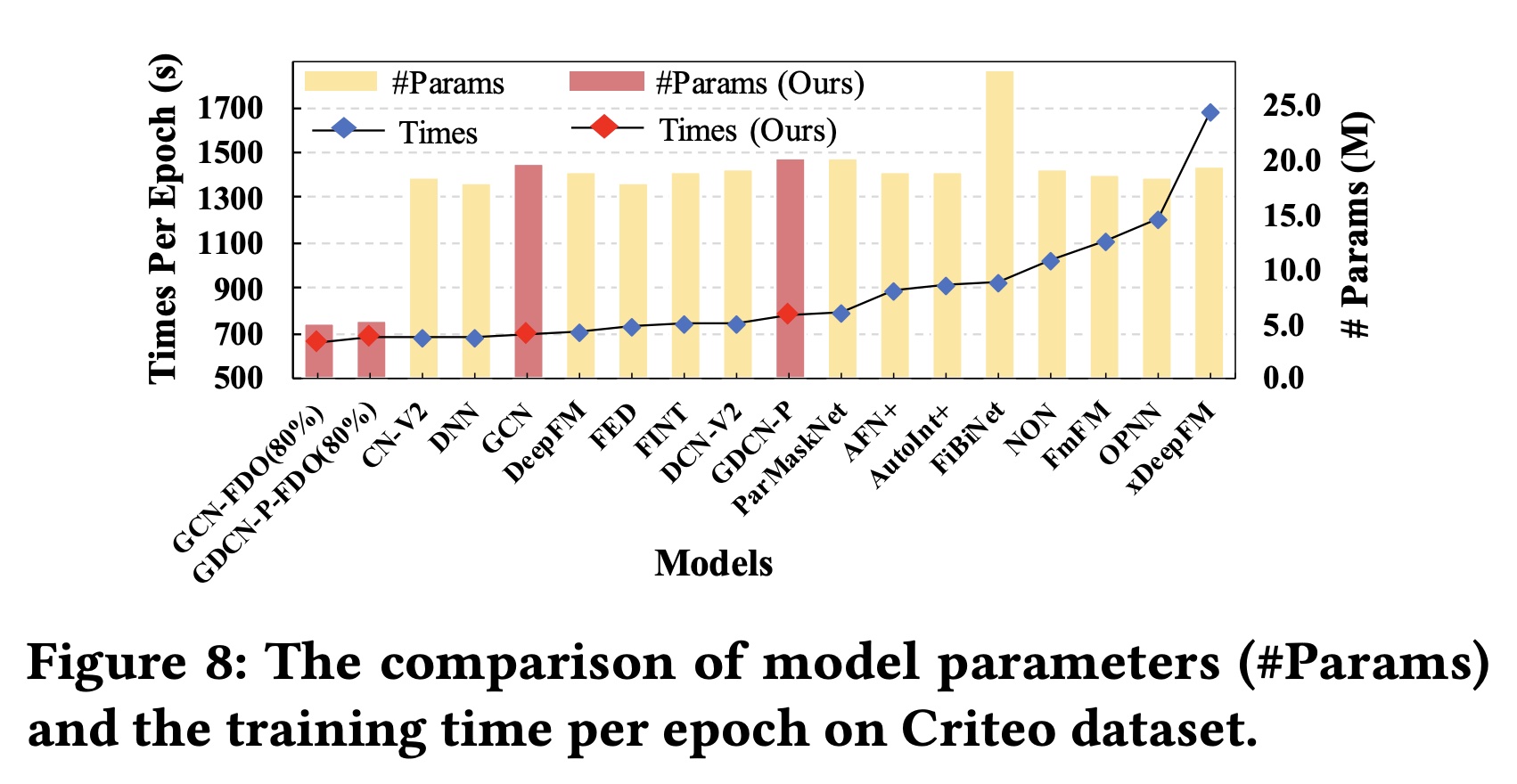
2. 内存和效率比较：在Criteo 数据集上，我们在删除低频特征后总共有1.086M 个特征。当使用固定维度（$K=16$$K=16$）时，embedding 参数约为17.4M 。如Figure 8 所示：

   • 大多数现有模型的参数范围从18M到20M，主要是由于embedding 参数。

   • 通过应用FDO ，我们可以直接减少embedding 参数。同时，GCN-FDO 和GDCN-PFDO 仅使用约5M 模型参数就实现了相媲美的准确率

   我们进一步比较了现有SOTA 模型的训练时间：

   • 未经维度优化的GCN 和GDCN的训练时间与DNN和DCN-V2相当。

   • 应用FDO 后，GCN-FDO和GDCN-P-FDO 以更少的参数和更快的训练速度超越了所有的SOTA 模型。

   

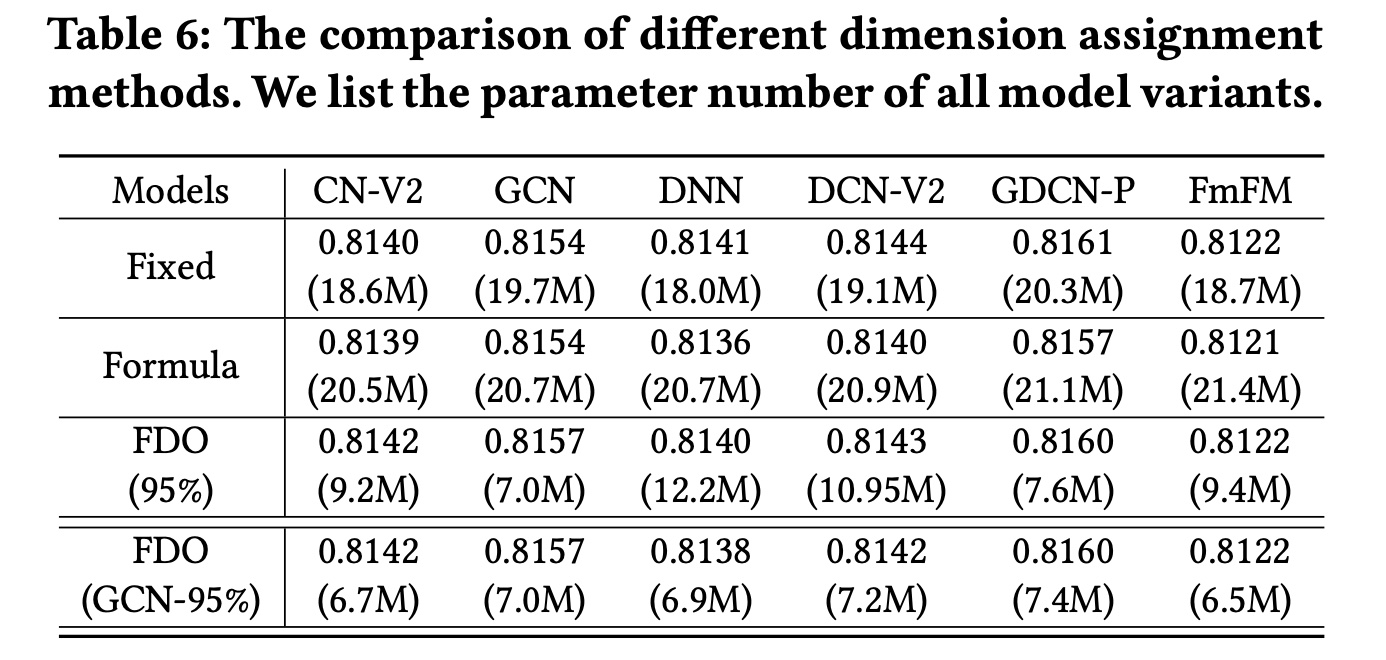
3. 兼容性分析：我们进一步将FDO应用于DNN、CNV2、DCN-V2 和FmFM，它们不需要相同的field 维度。此外，我们将FDO 与分配固定维度、以及FDO 章节中提到的分配不同维度的Formula method 进行了比较。Table 6 显示了结果。

   • 首先，Formula method 增加了模型参数并降低了其性能，因为它只考虑每个field 中的特征数量，而忽略了field 在训练过程中的重要性。相反，FDO 是一种后验方法，它通过在trained embedding table 中合并重要信息来学习field 维度。

   • 其次，将FDO应用于CN-V2和GCN 比base 模型获得了更好的性能。由于CN-V2 和GCN 主要关注显式的bit-level 特征交叉，FDO通过删除不必要的embedding 信息来refine field 维度。然而，将FDO 应用于包含DNN网络的DNN、DCN-V2和GDCN-P 会导致性能略有下降。

   • 最后，这些结果表明，我们可以使用FDO 基于SOTA 模型获取group field dimensions ，并将其复用为其他模型的默认维度。在Table 6 的最后一行，我们基于GCN学习了具有95% information ratio 的group field dimensions ，并将其应用于其他五个模型。与使用模型本身学到维度相比，这种方法实现了相媲美的性能，并且进一步减少了参数数量。

     可以只需要训练一次，就可以将 group field dimension 应用到多个模型，这降低了获取 group field dimension 的成本。

   

4. 对condensed field dimensions 的理解：通过FDO 学到的field 维度表明了相应field 的重要性。

   • 如Figure 7 所示，我们可以确定每个field 的平均重要性，例如field {#20, #23, #24} 很重要，而field {#11, #27, #30} 则不重要。

   • 参考Table 1 ，在应用95% information ratio 的FDO 后，field {#20, #23, #24} 确实具有更长的维度。相反，field {#11, #27, #30} 的维度较短。

   为了进一步验证这一观察结果，我们计算了第一层中averaged field importance 与 95% ratio 的optimization field dimensions 之间的皮尔逊相关系数。相关系数为0.82 ，p-value 小于 ${10}^{-9}$$10^{-9}$，这证实了field 维度与其各自重要性之间存在显著相关性。因此，我们可以直接从FDO 学到的field 维度粗略地识别哪些field 是重要的。

   请注意，field 维度并不总是与field 中的特征数量相关。例如，field {#16, #25} 具有最大的特征数量，但它们的field 维度很短，其重要性也不大。如果使用Formula method 分配field维度，则field {#16, #25} 将具有最长的维度。这种比较进一步凸显了所引入的FDO 方法的合理性和优越性。