一、 MultiEmbed [2023]

《On the Embedding Collapse When Scaling Up Recommendation Models》

1. foundation models 的最新进展催生了一个极具前景的趋势，即开发大型推荐模型以充分利用海量的可用数据。然而，主流推荐模型的规模仍然小得令人尴尬，且单纯扩大模型规模并不能带来足够的性能提升，这表明现有模型在 scalability 方面存在不足。在本文中，我们指出嵌入坍缩（embedding collapse）现象是阻碍 model scalability 的关键因素：embedding matrix 往往会占据一个低维子空间。通过实证分析和理论分析，我们揭示了 recommendation models 特有的 two-sided effect of feature interaction：

   • 一方面，interacting with collapsed embeddings 会限制 embedding learning，进而加剧 collapse 问题。

   • 另一方面，interaction 作为保障 scalability 的关键机制，在缓解过拟合方面发挥着至关重要的作用。

   即，interaction 具有两面性：好的一面是缓解过拟合，坏的一面是加剧 collapse 问题。

   基于上述分析，我们提出了一种简单而有效的 multi-embedding design，该设计融合了 embedding-set-specific interaction modules ，能够学习具有高度多样性的 embedding sets，从而减少 embedding collapse。大量实验表明，所提出的设计能够为各类推荐模型提供稳定的 scalability，并有效缓解 embedding collapse 问题。相关代码已开源至以下仓库：https://github.com/thuml/Multi-Embedding。

2. 推荐系统是重要的 machine learning 应用场景，其基于海量的 multi-field categorical data 来预测用户对 items 的行为。在日常生活中，推荐系统扮演着不可或缺的角色，帮助人们发现符合自身兴趣的信息，并已被广泛应用于电子商务、社交媒体、新闻推送和音乐流媒体等各类 online applications 中。研究人员已开发出基于 deep-learning 的推荐模型，能够灵活挖掘 feature representations。这些模型已成功部署于众多 application 场景，充分证明了其广泛的适用性和有效性。

   受 large foundation models 通过增加参数数量实现性能提升这一进展的启发，scale up 推荐模型规模以充分利用海量数据，这本应是一个极具前景的研究方向。然而，与直觉相悖的是，作为对性能起关键作用的核心组件，推荐模型的 embedding size 通常设置得极小（例如 《Bars: Towards open benchmarking for recommender systems》 中设置为 10 维），因此无法充分捕获数据中的丰富信息。更糟糕的是，如 Figure 1a 所示，增加 embedding size 不仅不能充分提升模型性能，甚至可能对模型造成负面影响。这表明：现有架构设计在 model scalability 方面存在缺陷，限制了推荐系统的性能上限。

   对于 DCNv2，模型性能虽然并未随着 embedding size 的增加而下降，但是它提升幅度非常低，几乎可以忽略不计。

   为探究这一现象背后的原因，我们通过奇异值分解（singular value decomposition）对学到的 embedding matrices 进行谱分析（spectral analysis），并在 Figure 1b 中展示了归一化后的奇异值（normalized singular values）。令人惊讶的是，大多数奇异值（singular values）都非常小，即学到的 embedding matrices 阵近乎低秩（low-rank ），我们将这一现象称为 embedding collapse 。随着模型规模的扩大，模型并未学习到更高维度的信息，这意味着参数利用效率（parameter utilization ）低下，进而限制了模型的 scalability 。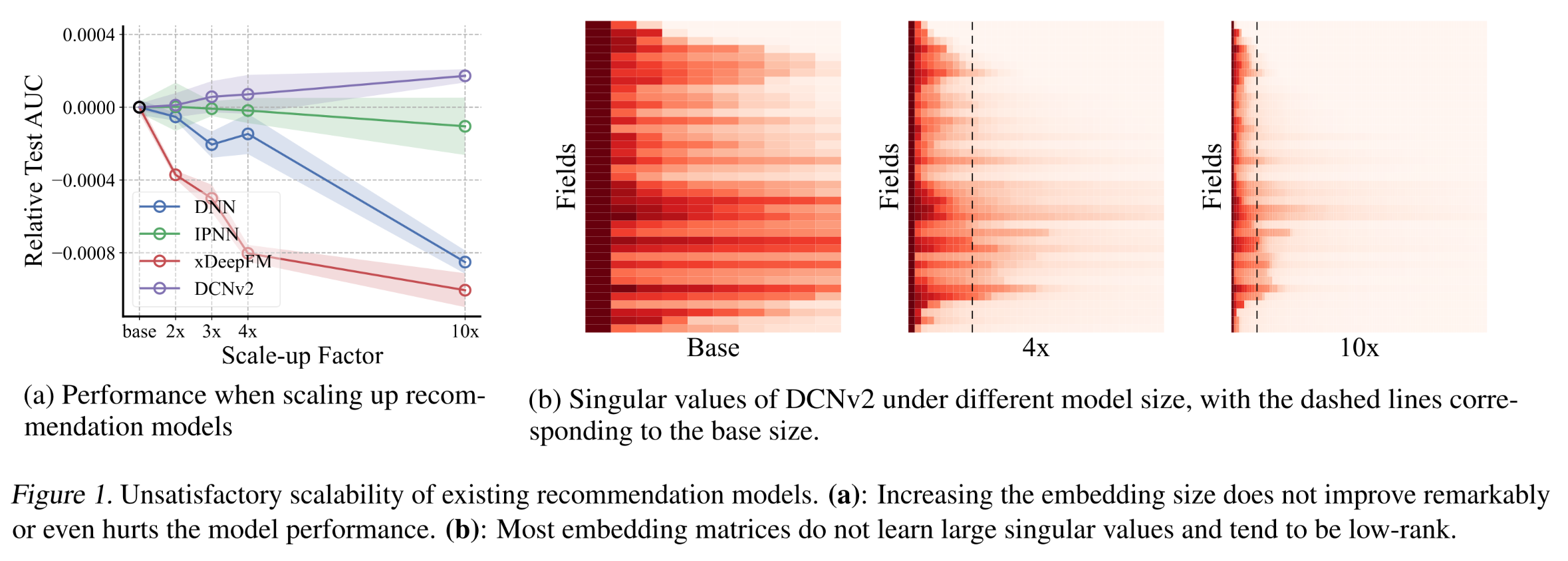

   

   在本文中，我们通过实证分析和理论分析深入研究了embedding collapse的形成机制，并揭示了作为推荐模型核心组件（用于建模 higher-order correlations ）的 feature interaction module 对 model scalability 的 two-sided effect ：

   • 一方面，interaction with collapsed embeddings 会限制 embedding learning ，进而加剧 embedding collapse 问题。

   • 另一方面，feature interaction 在 scaling up 模型规模时对减少 overfitting 至关重要，因此不能简单地限制或移除 feature interaction 模块。

   基于上述分析，我们得出了在不抑制 feature interaction 的前提下缓解 embedding collapse 的核心原则，从而为构建 scalable models 提供了理论依据。我们提出了 multi-embedding ，作为一种简单而高效的 model scaling 机制。multi-embedding 通过增加独立的 embedding sets 的数量，并融合 embedding-set-specific interaction modules，从而共同捕获不同的模式。实验结果表明，multi-embedding 能够为各类主流推荐模型提供 scalability，并显著缓解 multi-embedding 问题，为突破推荐系统的 size limit 提供了一种有效方法。

   本文的主要贡献如下：

   • 据我们所知，我们首次指出了推荐系统中的 model scalability 问题，并发现了 embedding collapse 现象。 embedding collapse 是提升推荐模型 scalability 亟需解决的关键问题。

   • 通过实证分析和理论分析，我们基于 embedding collapse 现象揭示了 feature interaction 过程对 model scalability 的 two-sided effect ：feature interaction 会导致 embedding collapse ，但同时提供了必要的对抗过拟合的能力。

   • 基于 “在不抑制 feature interaction 的前提下缓解 embedding collapse ” 这一核心原则，我们提出了一种统一的 multi-embedding 设计。该设计能够持续提升各类 SOTA 推荐模型的 scalability ，并有效缓解 embedding collapse 问题。

1.1 相关工作

1. 推荐系统中的模块：已有大量工作研究推荐系统的模块设计。一类研究专注于 feature interaction 过程，其中 feature interaction 是推荐系统特有的。这些工作旨在融合推荐系统的 domain-specific knowledge 。我们的工作不是提出新的模块，而是从机器学习的角度出发，分析现有模型的 scalability。

2. Collapse 现象：neural collapse 或 representation collapse 描述了 representation vectors 的退化。这一现象在监督学习、无监督对比学习、迁移学习、以及 generative models 中得到了广泛研究。《On the representation collapse of sparse mixture of experts》 讨论了 sparse MoEs 中的 representation collapse 。受这些工作的启发，我们将 embedding vectors 视为 representations ，从而认识到推荐模型中的 embedding collapse 现象。然而，我们面临的是 field-level interaction 的场景，这在之前的研究中尚未得到充分探讨。

3. 固有维度和压缩理论：为描述数据的复杂性，现有工作包括基于固有维度（intrinsic-dimension ）的量化、以及基于剪枝的分析。我们提出的 SVD-based 的信息丰度（information abundance）概念与这些工作相关。

1.2 预备知识

1. 推荐模型旨在基于多个 fields 的特征来预测 user action。在本文中，我们考虑推荐系统的基本场景，涉及 categorial features 和 binary outputs 。形式化地，假设存在 $N$$N$ 个 fields, ，第 $i$$i$ 个 field 表示为 ${\mathcal{X}}_i=\{1,2,\cdots ,D_i\}$$\mathcal X_{i} = \{1, 2, \cdots, D_{i}\}$，其中 $D_i$$D_{i}$ 表示该 field 的 cardinality 。令：

   $$\mathcal{X}={\mathcal{X}}_1\times {\mathcal{X}}_2\times \cdots \times {\mathcal{X}}_N,\mathcal{Y}=\{0,1\}$$

   则推荐模型的目标是：学习从 $\mathcal{X}$$\mathcal X$ 到 $\mathcal{Y}$$\mathcal Y$ 的映射。

2. 除了考虑来自各种各样的 fields 的单个特征外，推荐系统领域已有大量研究通过 feature interaction 模块来建模 combined features 。在本文中，我们研究了主流推荐模型广泛采用的以下架构：一个推荐模型通常包含：

   • (1)：每个 field 的 embedding layer ${\mathbf{E}}_i\in {\mathbb{R}}^{D_i\times K}$$\mathbf E_{i} \in \mathbb{R}^{D_{i} \times K}$，其中 $K$$K$ 为 embedding size ，$i\in \{1,2,\cdots ,N\}$$i\in \{1,2,\cdots, N\}$。

   • (2)：一个 interaction 模块 $I$$I$，负责将所有 embeddings 整合为 a combined feature scalar or vector 。

   • (3)：一个后续的 postprocessing 模块 $F$$F$，用于预测（例如 MLP 和 MoE）。

   该模型的前向传播（forward pass ）过程可形式化为：

   $$\begin{array}{c}{\overrightarrow{\mathbf{e}}}_i={\mathbf{E}}_i^{\mathrm{\top }}{\overrightarrow{\mathbf{1}}}_{x_i},\mathrm{\forall }i\in \{1,2,\cdots ,N\}\\ \overrightarrow{\mathbf{h}}=I({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)\\ \hat{y}=F\left(\overrightarrow{\mathbf{h}}\right)\end{array}$$

   其中： ${\overrightarrow{\mathbf{1}}}_{x_i}\in {\mathbb{R}}^{D_i}$$\mathbf{\vec 1}_{x_{i}}\in \mathbb R^{D_i}$ 表示 $x_i\in {\mathcal{X}}_i$$x_{i} \in \mathcal X_{i}$ 的 one-hot encoding 。即， ${\overrightarrow{\mathbf{e}}}_i$$\mathbf{\vec e}_{i}$ 是 embedding table ${\mathbf{E}}_i$$\mathbf E_{i}$ 第 $x_i$$x_{i}$ 行的转置。

1.3 Embedding Collapse

1. 奇异值分解（singular value decomposition）已被广泛用于衡量 collapse 现象（《Understanding dimensional collapse in contrastive self-supervised learning》）。在 Figure 1b 中，我们展示了推荐模型学到的 embedding matrices 接近 low-rank ，且存在一些极小的奇异值（singular values）。为了量化这类具有低秩（low-rank）倾向的矩阵的 collapse程度，我们提出了信息丰度（information abundance）作为一种广义的度量指标。

   

2. 信息丰度的定义：考虑矩阵 $\mathbf{E}\in {\mathbb{R}}^{D\times K}$$\mathbf E \in \mathbb{R}^{D \times K}$ 及其奇异值分解 $\mathbf{E}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{\top }}=\sum _{k=1}^K{\sigma }_k{\overrightarrow{\mathbf{u}}}_k{\overrightarrow{\mathbf{v}}}_k^{\mathrm{\top }}$$\mathbf E = \mathbf U\mathbf \Sigma \mathbf V^{\top} = \sum_{k=1}^{K} \sigma_{k} \mathbf{\vec u}_{k} \mathbf{\vec v}_{k}^{\top}$，其中 $K\le D$$K\le D$ ，则 $\mathbf{E}$$\mathbf E$ 的信息丰度定义为：

   $$\text{IA}(\mathbf{E})=\frac{{\Vert \overrightarrow{\sigma }\Vert }_1}{{\Vert \overrightarrow{\sigma }\Vert }_{\mathrm{\infty }}}$$

   即，所有奇异值的和除以最大奇异值。

   其中：

   • $\{{\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_K\}$$\{\sigma_1,\sigma_2,\cdots,\sigma_K\}$ 为 $K$$K$ 个奇异值，${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_K\ge 0$$\sigma_1\ge\sigma_2\ge\cdots\ge \sigma_K \ge 0$ 。

     因此有，$\text{IA}(\mathbf{E})=\frac{\sum _{k=1}^K{\sigma }_k}{{\sigma }_1}\ge 1$$\text{IA}(\mathbf E) = \frac{\sum_{k=1}^K\sigma_k}{\sigma_1}\ge 1$ 。当 $\text{IA}(\mathbf{E})=1$$\text{IA}(\mathbf E) = 1$ 时，意味着 ${\sigma }_2=\cdots ={\sigma }_K=0$$\sigma_2 = \cdots = \sigma_K = 0$ 。

   • $\overrightarrow{\sigma }=({\sigma }_1,\cdots ,{\sigma }_K)\in {\mathbb{R}}^K$$\mathbf{\vec \sigma} = (\sigma_1,\cdots,\sigma_K)\in \mathbb R^K$ 为 $K$$K$ 个奇异值组成的向量。

   • $\mathbf{\Sigma }=\text{diag}({\sigma }_1,\cdots ,{\sigma }_K)\in {\mathbb{R}}^{D\times K}$$\mathbf\Sigma = \text{diag}(\sigma_1,\cdots,\sigma_K)\in \mathbb R^{D\times K}$ 为 $K$$K$ 个奇异值组成的对角化矩阵，仅对角线存在非零元素，其他位置均为零。

   • $\mathbf{U}\in {\mathbb{R}}^{D\times D}$$\mathbf U\in \mathbb R^{D\times D}$ 是 $D$$D$ 阶正交矩阵，$\mathbf{U}{\mathbf{U}}^{\mathrm{\top }}=\mathbf{I}$$\mathbf U\mathbf U^\top = \mathbf I$，${\overrightarrow{\mathbf{u}}}_k\in {\mathbb{R}}^{D\times 1}$$\mathbf{\vec u}_k\in \mathbb R^{D\times 1}$ 为 $\mathbf{U}$$\mathbf U$ 的第 $k$$k$ 个列向量。$\mathbf{U}$$\mathbf U$ 的所有列向量称为左奇异向量（left singular vector）。

   • $\mathbf{V}\in {\mathbb{R}}^{K\times K}$$\mathbf V\in \mathbb R^{K\times K}$ 是 $K$$K$ 阶正交矩阵，$\mathbf{V}{\mathbf{V}}^{\mathrm{\top }}=\mathbf{I}$$\mathbf V\mathbf V^\top = \mathbf I$，${\overrightarrow{\mathbf{v}}}_k\in {\mathbb{R}}^{K\times 1}$$\mathbf{\vec v}_k\in\mathbb R^{K\times 1}$ 为 $\mathbf{V}$$\mathbf V$ 的第 $k$$k$ 个列向量。$\mathbf{V}$$\mathbf V$ 的所有列向量称为右奇异向量（right singular vector）。

3. 直观地，信息丰度高的矩阵在向量空间中具有均衡的分布（因为其 singular values 较为接近）。相反，信息丰度低的矩阵表明，对应于较小奇异值的分量可以被压缩，而不会对结果产生显著影响。与矩阵秩（matrix rank）相比，信息丰度可以看作是一种简单扩展（注意 $\text{rank}(\mathbf{E})={\Vert \overrightarrow{\sigma }\Vert }_0$$\text{rank}(\mathbf E) = \left\|\vec \sigma\right\|_{0}$，表示非零的奇异值的个数），但它适用于非严格低秩矩阵（non-strictly low-rank matrices ），尤其是对于 fields 数量 $D_i$$D_i$ 满足 $D_i\gg K$$D_{i} \gg K$（可能为 rank K ）。

   我们计算了扩大规模后的 DCNv2 （《DCN V2: Improved Deep & Cross Network and Practical Lessons for Web-scale Learning to Rank Systems》）的 embedding matrices 的信息丰度，并与随机初始化的矩阵进行了比较，结果如 Figure 2 所示。可以观察到，学到的 embedding matrices 的信息丰度极低，这表明存在 embedding collapse 现象。

   这是按照随机初始化方法中信息丰度从大到小来排序 Fields。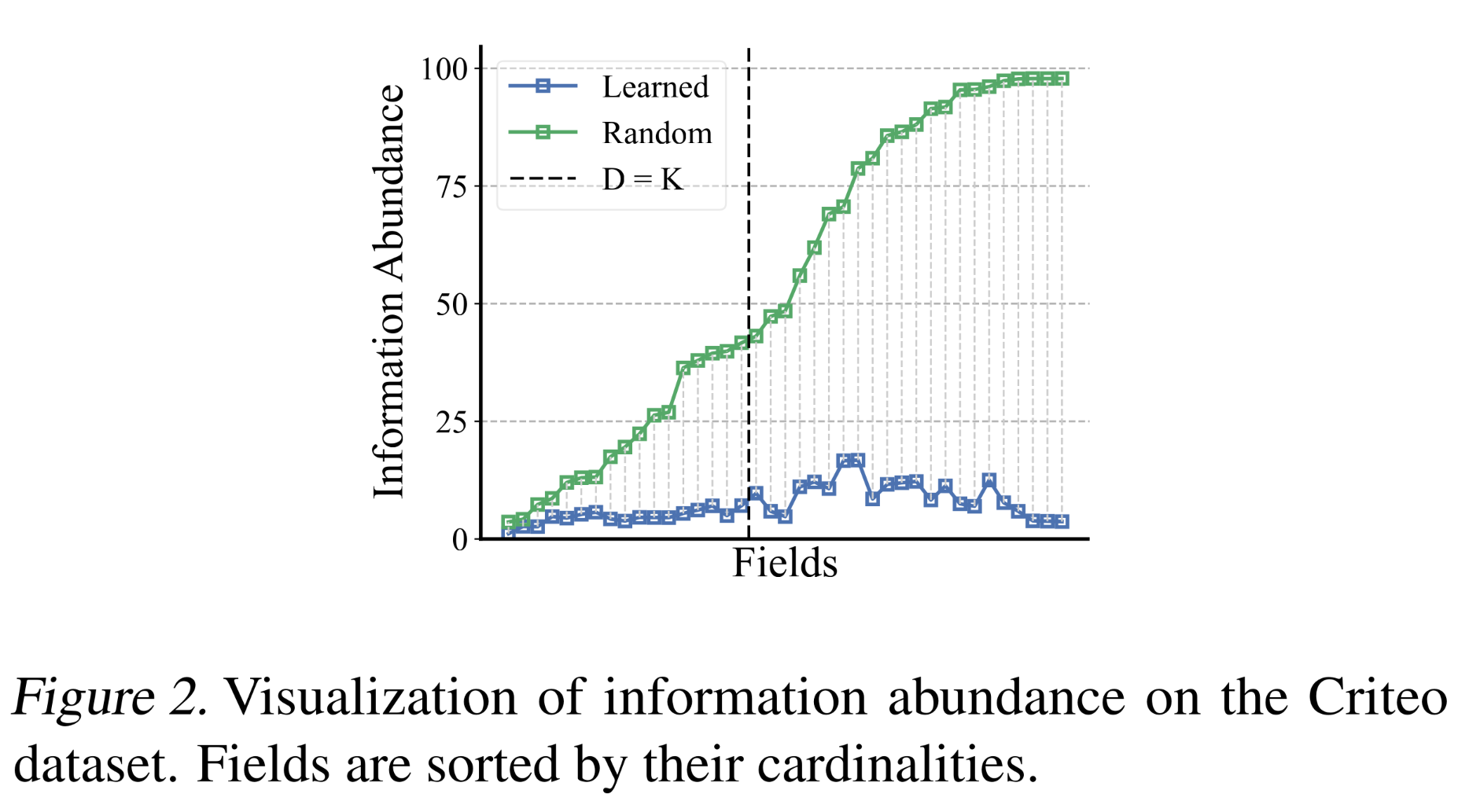

   

1.4 Feature Interaction Revisited

1. 在本节中，我们深入探讨推荐模型中的 embedding collapse 现象。我们重新审视了作为推荐模型核心的 feature interaction 模块，并围绕以下两个问题展开研究：

   • (1)：embedding collapse 是如何产生的？

   • (2)：如何有效缓解 embedding collapse 并提升model scalability ？

   通过实证研究和理论研究，我们揭示了 feature interaction 模块对 model scalability 的 two-sided effect 。

1.4.1 Interaction-Collapse Theory

1. 为了确定 feature interaction 如何导致 embedding collapse ，直接分析原始 embedding matrices 是不够的：因为学到的embedding matrix 是 interactions with all other fields 的结果，因此难以分离 impact of field-pair-level interaction 对 embedding learning 的影响。为解决这一难题，我们通过对 models with sub-embeddings 进行实证分析，并对一般模型进行理论分析，得出 feature interaction 会导致 embedding collapse 的结论，我们将其称为 interaction-collapse theory 。

   • 为什么直接分析原始 embedding matrices 是不够的？

     因为只看最终的 embedding 矩阵的话，难以判断 embedding collapse 到底是由于 field 本身引起的，还是由于与其它 field 的交互所引起的。

   • 而为什么分析 models with sub-embeddings 是可行的？

     因为每个 sub-embedding 专门用于 field pair 之间的交互。从而有助于判断 embedding collapse 到底是由于 field 本身引起的，还是由于与其它 field 的交互所引起的。

2. Evidence I: Empirical analysis on models with sub-embeddings：DCNv2 通过在每个 field pair 之上引入一个 crossing network （由 transformation 矩阵 ${\mathbf{W}}_{i\to j}$$\mathbf W_{i\rightarrow j}$ 来参数化），对 field $i$$i$ 的 embedding vector 进行投影，然后 field $i$$i$ 再与 field $j$$j$ 进行交互。通过收集 all projected embedding vectors ，DCNv2 可以被视为从 embedding matrix ${\mathbf{E}}_i$$\mathbf E_{i}$ 中隐式地生成 field-aware sub-embeddings ${\mathbf{E}}_i^{\to 1},{\mathbf{E}}_i^{\to 2},\cdots ,{\mathbf{E}}_i^{\to N}$$\mathbf E_{i}^{\to 1}, \mathbf E_{i}^{\to 2}, \cdots, \mathbf E_{i}^{\to N}$，从而与所有 fields 进行交互。这些 field-aware sub-embeddings 的形式为：

   $${\mathbf{E}}_i^{\to j}={\mathbf{E}}_i{\mathbf{W}}_{i\to j}^{\mathrm{\top }}$$

   DCNv2 由多个堆叠的 cross layers 组成，为简化分析，我们仅讨论第一层。为了确定 sub-embedding matrices 的 collapse 程度，我们计算了所有 $(i,j)$$(i,j)$ pairs 的 $\text{IA}\left({\mathbf{E}}_i^{\to j}\right)$$\text{IA}\left(\mathbf E_{i}^{\to j}\right)$，结果如 Figure 3a 所示。为方便起见，我们根据信息丰度的升序对 field indices 进行预排序，即根据 $\text{IA}({\mathbf{E}}_i)$$\text{IA}(\mathbf E_{i})$ 对 $i$$i$ 进行排序（$j$$j$ 的排序方式类似）。

   • 可以观察到， $\text{IA}\left({\mathbf{E}}_i^{\to j}\right)$$\text{IA}\left(\mathbf E_{i}^{\to j}\right)$ 大致沿 $i$$i$ 呈上升趋势——这是显而易见的，因为 ${\mathbf{E}}_i^{\to j}$$\mathbf E_{i}^{\to j}$ 只是 ${\mathbf{E}}_i$$\mathbf E_{i}$ 的投影。

     注意，横轴的 field 是根据 $\text{IA}({\mathbf{E}}_i)$$\text{IA}(\mathbf E_{i})$ 对 $i$$i$ 进行排序（$j$$j$ 的排序方式类似）的。

   • 有趣的是，我们还观察到另一种相关性（correlation）：sub-embeddings 的信息丰度受到其交互的 fields 的共同影响，表现为沿 $j$$j$ 的上升趋势（尤其是对于较大的 $i$$i$）。例如，我们进一步计算了 $\text{IA}\left({\mathbf{E}}_i^{\to j}\right)$$\text{IA}\left(\mathbf E_{i}^{\to j}\right)$ 对 $j$$j$ 或 $i$$i$ 的求和，以研究单个变量的影响，结果如 Figure 3b 和 Figure 3c 所示。上升趋势和相关系数证实了 $i$$i$ 和 $j$$j$ 的共同影响。

   我们还对同样包含 sub-embeddings 的 FFM 模型的信息丰度进行了分析，得到了类似的观察结果（见附录 H）。

   这一段的核心结论是：sub-embeddings 的信息丰度受到其交互的 fields 的共同影响。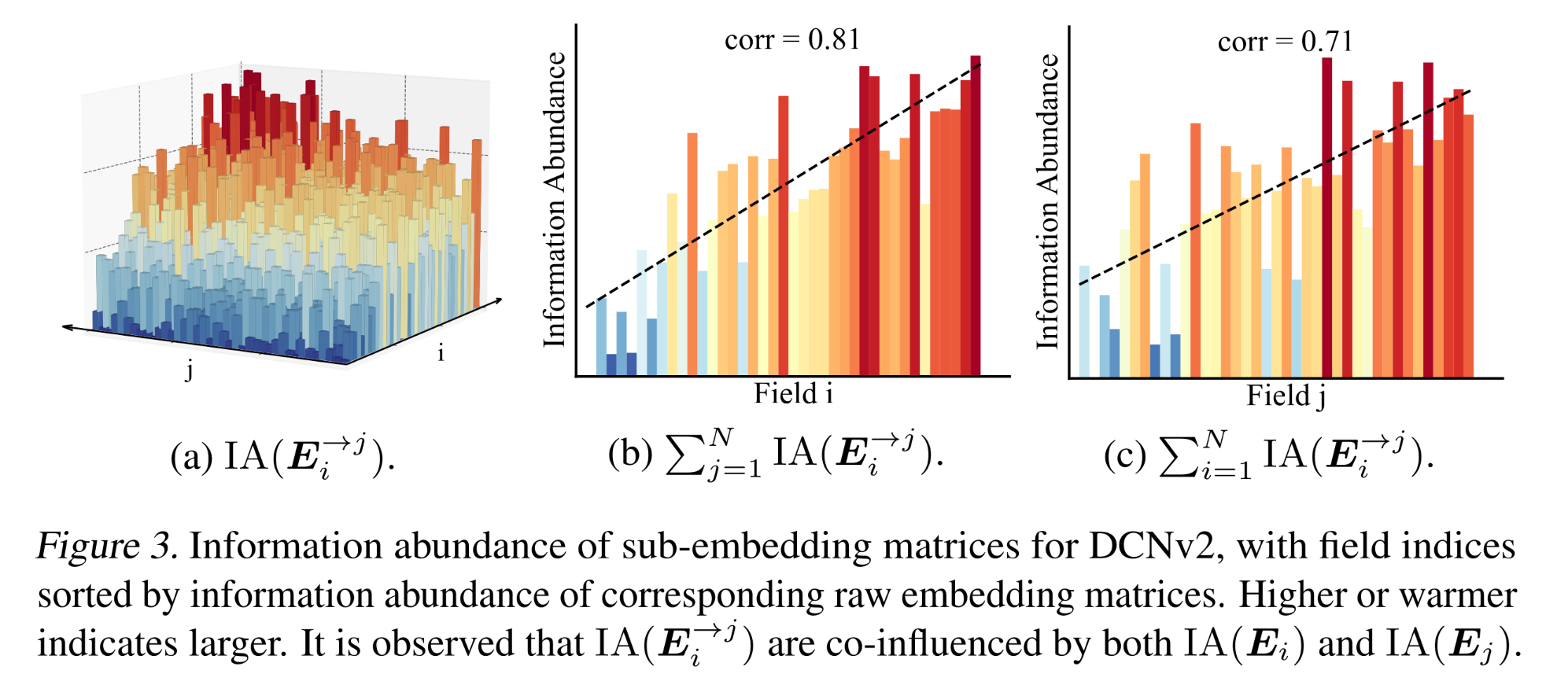

   

3. Evidence II: Theoretical analysis on general recommendation models：现在，我们从理论上证明，即使没有 sub-embedding ，一般模型中的 feature interaction 也会导致 embedding collapse 。为简化分析，我们考虑 FM 风格的 feature interaction 。形式化地，feature interaction 过程定义为：

   $$h=\sum _{i=1}^N\sum _{j=1}^{i-1}{\overrightarrow{\mathbf{e}}}_i^{\mathrm{\top }}{\overrightarrow{\mathbf{e}}}_j=\sum _{i=1}^N\sum _{j=1}^{i-1}{\overrightarrow{\mathbf{1}}}_{x_i}^{\mathrm{\top }}{\mathbf{E}}_i{\mathbf{E}}_j^{\mathrm{\top }}{\overrightarrow{\mathbf{1}}}_{x_j}$$

   其中：$h$$h$ 是前面提到的组合特征（combined feature）。

   不失一般性，我们讨论 ${\mathbf{E}}_1$$\mathbf E_{1}$ 的特定行 ${\overrightarrow{\mathbf{e}}}_1$$\mathbf{\vec e}_{1}$，并保持其他 embedding matrices 的 fixed 的。考虑一个 batch size = B 的 mini-batch。令 ${\sigma }_{i,k}$$\sigma_{i, k}$ 为 ${\mathbf{E}}_i$$\mathbf E_{i}$ 的第 $k$$k$ 个奇异值，${\overrightarrow{\mathbf{u}}}_{i,k}$$\mathbf{\vec u}_{i, k}$、${\overrightarrow{\mathbf{v}}}_{i,k}$$\mathbf{\vec v}_{i, k}$ 为对应的左奇异向量和右奇异向量。我们有：

   $$\begin{array}{c}\frac{\partial L}{\partial {\overrightarrow{\mathbf{e}}}_1}=\frac{1}{B}\sum _{b=1}^B\frac{\partial {\ell }^{(b)}}{\partial h^{(b)}}\times \frac{\partial h^{(b)}}{\partial {\overrightarrow{\mathbf{e}}}_1}=\frac{1}{B}\sum _{b=1}^B\frac{\partial {\ell }^{(b)}}{\partial h^{(b)}}\times \left(\sum _{i=2}^N{\mathbf{E}}_i^{\mathrm{\top }}{\overrightarrow{\mathbf{1}}}_{x_i^{(b)}}\right)\\ =\frac{1}{B}\sum _{b=1}^B\frac{\partial {\ell }^{(b)}}{\partial h^{(b)}}\times \left(\sum _{i=2}^N\sum _{k=1}^K{\sigma }_{i,k}{\overrightarrow{\mathbf{v}}}_{i,k}{\overrightarrow{\mathbf{u}}}_{i,k}^{\mathrm{\top }}{\overrightarrow{\mathbf{1}}}_{x_i^{(b)}}\right)\\ =\sum _{i=2}^N\sum _{k=1}^K\left(\frac{1}{B}\sum _{b=1}^B\frac{\partial {\ell }^{(b)}}{\partial h^{(b)}}{\overrightarrow{\mathbf{u}}}_{i,k}^{\mathrm{\top }}{\overrightarrow{\mathbf{1}}}_{x_i^{(b)}}\right){\sigma }_{i,k}{\overrightarrow{\mathbf{v}}}_{i,k}\\ =\sum _{i=2}^N\sum _{k=1}^K{\alpha }_{i,k}{\sigma }_{i,k}{\overrightarrow{\mathbf{v}}}_{i,k}=\sum _{i=2}^N{\overrightarrow{\theta }}_i\\ \text{ where : }{\alpha }_{i,k}=\left(\frac{1}{B}\sum _{b=1}^B\frac{\partial {\ell }^{(b)}}{\partial h^{(b)}}{\overrightarrow{\mathbf{u}}}_{i,k}^{\mathrm{\top }}{\overrightarrow{\mathbf{1}}}_{x_i^{(b)}}\right),{\overrightarrow{\theta }}_i=\sum _{k=1}^K{\alpha }_{i,k}{\sigma }_{i,k}{\overrightarrow{\mathbf{v}}}_{i,k},{\overrightarrow{\sigma }}_i=({\sigma }_{i,1},\cdots ,{\sigma }_{i,K})\end{array}$$

   该方程表明，梯度可以分解为 field-specific 的项。我们考虑某个 field $i$$i$ 的梯度分量 ${\overrightarrow{\theta }}_i$$\vec \theta_{i}$，它可以进一步分解为对应 embedding matrix ${\mathbf{E}}_i$$\mathbf E_{i}$ 的谱分量。从 ${\overrightarrow{\theta }}_i$$\vec \theta_{i}$ 的形式可以看出，${\alpha }_{i,k}$$\alpha_{i, k}$ 是与 ${\overrightarrow{\sigma }}_i$$\vec \sigma_{i}$ 无关的标量，由 training data 和 objective function 决定。因此，${\overrightarrow{\sigma }}_i$$\vec \sigma_{i}$ 的 variety 显著影响梯度分量 ${\overrightarrow{\theta }}_i$$\vec \theta_{i}$ 的构成。对于较大的 ${\sigma }_{i,k}$$\sigma_{i, k}$，在梯度分量 ${\overrightarrow{\theta }}_i$$\vec \theta_{i}$ 上，对应的谱 ${\overrightarrow{\mathbf{v}}}_{i,k}$$\mathbf{\vec v}_{i, k}$ 上赋予更大的权重。当 ${\mathbf{E}}_i$$\mathbf E_{i}$ 的信息丰度较低时，梯度分量 ${\overrightarrow{\theta }}_i$$\vec \theta_{i}$ 的权重不平衡，导致 ${\overrightarrow{\mathbf{e}}}_1$$\mathbf{\vec e}_{1}$ 退化。

   类似地，因此 ${\mathbf{E}}_1$$\mathbf E_{1}$ 的所有行都会以类似的方式退化，最终形成 a collapsed matrix。

   当 ${\mathbf{E}}_i$$\mathbf E_i$ 信息丰度低时，其奇异值 ${\sigma }_{i,k}$$\sigma_{i,k}$ 的分布极不均衡，大部分 ${\sigma }_{i,k}$$\sigma_{i,k}$ 为零，只有少部分非零。这意味着在求和 $\sum _{k=1}^K{\alpha }_{i,k}{\sigma }_{i,k}{\overrightarrow{\mathbf{v}}}_{i,k}$$\sum_{k=1}^K \alpha_{i,k}\sigma_{i,k} \mathbf{\vec v}_{i,k}$ 中：

   • 对应于大奇异值 ${\sigma }_{i,k^{\ast }}$$\sigma_{i, k^*}$ 的项 ${\alpha }_{i,k^{\ast }}{\sigma }_{i,k^{\ast }}{\overrightarrow{\mathbf{v}}}_{i,k^{\ast }}$$\alpha_{i,k^*}\sigma_{i,k^*} \mathbf{\vec v}_{i,k^*}$ 会占据绝对主导地位。

   • 对应于小奇异值的项贡献微乎其微。

   因此，梯度分量 ${\overrightarrow{\theta }}_i$$\vec \theta_i$ 的方向几乎完全由那几个最大的 ${\overrightarrow{\mathbf{v}}}_{i,k^{\ast }}$$\mathbf{\vec v}_{i,k^*}$ 决定，而不是所有 ${\left\{{\overrightarrow{\mathbf{v}}}_{i,k}\right\}}_{k=1}^K$$\left\{\mathbf{\vec v}_{i,k}\right\}_{k=1}^K$ 的均衡组合。这就是“权重不平衡”。

   梯度 $\frac{\partial L}{\partial {\overrightarrow{\mathbf{e}}}_1}$$\frac{\partial L}{\partial \mathbf{\vec e}_1}$ 指导着 ${\overrightarrow{\mathbf{e}}}_1$$\mathbf{\vec e}_1$ 的更新方向。如果其中某个分量 ${\overrightarrow{\theta }}_i$$\vec \theta_i$ 被限制在少数几个方向上，那么 ${\overrightarrow{\mathbf{e}}}_1$$\mathbf{\vec e}_1$ 为了最小化损失，其更新也会被“拉向”这些方向。这限制了 ${\overrightarrow{\mathbf{e}}}_1$$\mathbf{\vec e}_1$ 在其他正交方向上的探索和学习，使其表达能力受限，即发生“退化”。长此以往，${\overrightarrow{\mathbf{e}}}_1$$\mathbf{\vec e}_1$ 也会倾向于落在这几个主导方向张成的低维子空间里。

   刚开始 ${\mathbf{E}}_i$$\mathbf E_i$ 随机初始化的时候，信息丰度不低。随着训练的进行，${\mathbf{E}}_i$$\mathbf E_i$ 的信息丰度可能下降（比如过拟合、或者噪音）。

   为进一步说明，我们在合成数据上进行了一个简单实验。假设存在 $N=3$$N=3$ 个 fields，我们将 $D_3$$D_{3}$ 设置为不同的值（$D_3<K$$D_{3} < K$ 和 $D_3\gg K$$D_{3} \gg K$），以模拟低信息丰度和高信息丰度的情况——这与现实场景中 field cardinality 的 diverse range 相符。我们在保持 ${\mathbf{E}}_2$$\mathbf E_{2}$、${\mathbf{E}}_3$$\mathbf E_{3}$ 固定的情况下训练 ${\mathbf{E}}_1$$\mathbf E_{1}$。实验设置的详细信息见附录 G。Figure 4 展示了两种情况下 ${\mathbf{E}}_1$$\mathbf E_{1}$ 的信息丰度随训练过程的变化。可以观察到，与 low-information-abundance matrix 进行交互会导致 a collapsed embedding 。

   当 $D_3<K$$D_3\lt K$ 时，${\mathbf{E}}_3$$\mathbf E_3$ 的秩小于等于 $D_3$$D_3$ ，因此最多有 $D_3$$D_3$ 个非零的奇异值。当 $D_3\gg K$$D_3\gg K$ 时，${\mathbf{E}}_3$$\mathbf E_3$ 的秩小于等于 $K$$K$ ，因此最多有 $K$$K$ 个非零的奇异值。

   在固定 $K$$K$ 的情况下，第一种情况有更低的 $\text{IA}({\mathbf{E}}_3)$$\text{IA}(\mathbf E_3)$ 。而更低的 $\text{IA}({\mathbf{E}}_3)$$\text{IA}(\mathbf E_3)$ 会导致更低的 $\text{IA}({\mathbf{E}}_1)$$\text{IA}(\mathbf E_1)$。这是因为低信息丰度的 embedding 矩阵会通过特征交互的梯度传播机制，限制其他字段 embedding 的学习空间，导致其也趋向坍塌。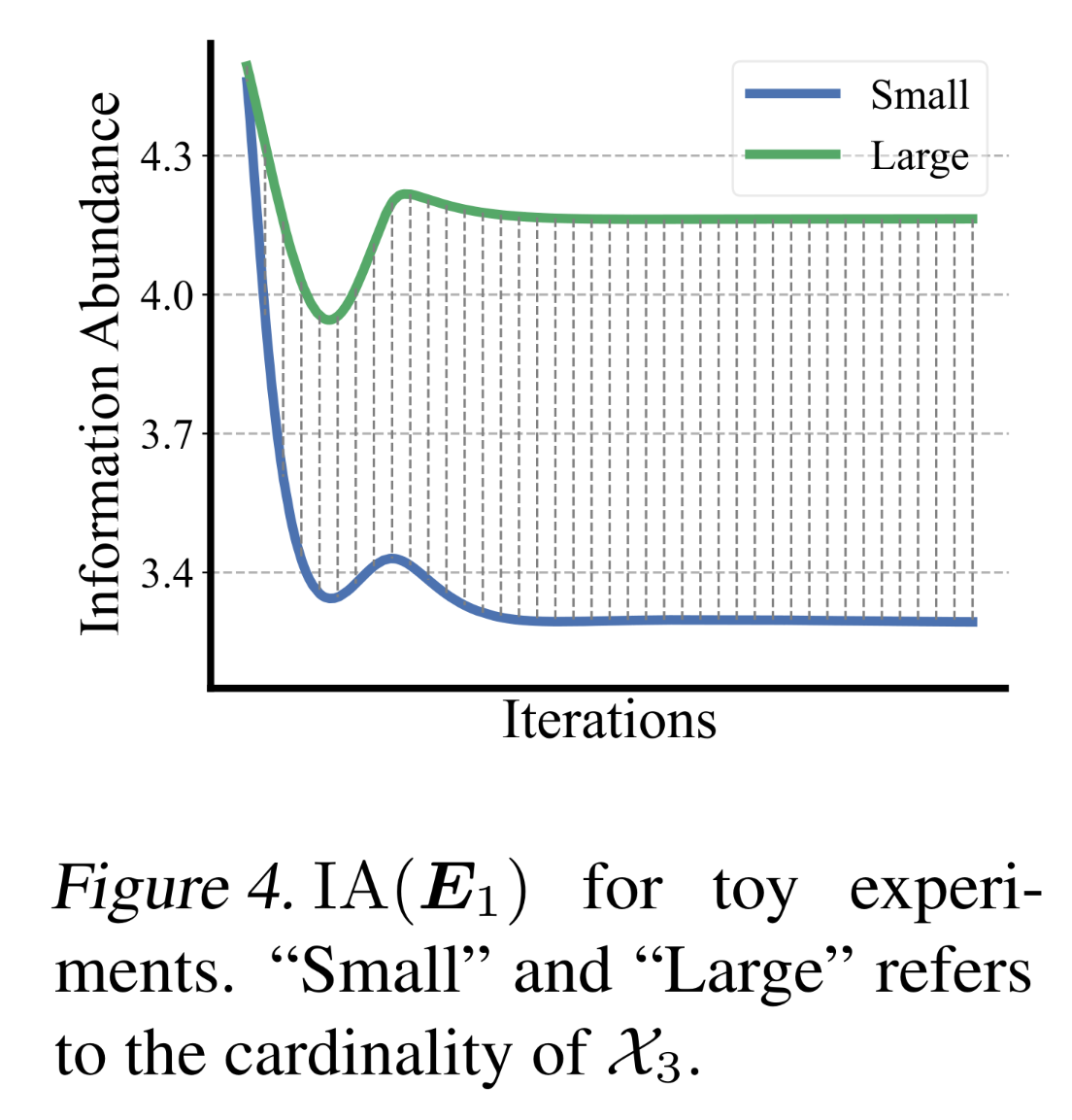

   

4. Summary: How is collapse caused in recommendation models?：Evidence I 表明，与 low-information-abundance field 进行交互会导致 a more collapsed sub-embedding 。考虑到 sub-embeddings 源于原始 embeddings ，反映了 fields interact 的影响，我们认识到 feature interaction 导致 embedding collapse 的内在机制——这一机制得到了我们理论分析的进一步证实。我们得出 interaction-collapse theory ：

   • Finding 1 (Interaction-Collapse Theory)：在推荐模型的 feature interaction 中，fields with low-information-abundance embeddings 会限制其他 fields 的信息丰度，导致 collapsed embedding matrices 。

   interaction-collapse theory 表明，feature interaction 是导致 embedding collapse 的主要诱因，从而限制了模型的理想的 scalability 。

1.4.2 避免 Collapse 是否足以实现 Scalability ?

1. 根据上述讨论，我们已经表明推荐模型的 feature interaction 过程会导致 embedding collapse ，进而限制模型的 scalability。现在我们讨论其逆命题：即抑制 feature interaction 以缓解 embedding collapse 是否会带来模型 scalability 的提升？为回答这一问题，我们设计了以下两个实验，对比标准模型、以及 feature interaction 被抑制的模型。

2. Evidence III: Limiting the modules in interaction that leads to collapse：Evidence I 表明，投影矩阵 ${\mathbf{W}}_{i\to j}$$\mathbf W_{i \to j}$ 会被学习从而调整 sub-embeddings 的信息丰度，从而导致 embedding collapse。现在，我们通过引入以下带有可学习参数 ${\lambda }_{ij}$$\lambda_{ij}$ 的正则化项，研究抑制这种效应如何影响 model scalability：

   $${\ell }_{\text{reg}}=\sum _{i=1}^N\sum _{j=1}^N{\Vert {\mathbf{W}}_{i\to j}^{\mathrm{\top }}{\mathbf{W}}_{i\to j}-{\lambda }_{ij}\mathbf{I}\Vert }_F^2$$

   其中：$\mathbf{I}$$\mathbf I$ 为单位矩阵。

   该正则化项将投影矩阵 ${\mathbf{W}}_{i\to j}$$\mathbf W_{i \to j}$ 约束为酉矩阵的乘积。这样， ${\mathbf{W}}_{i\to j}$$\mathbf W_{i \to j}$ 将保留所有归一化奇异值（normalized singular values），并在投影后保持信息丰度。我们在不同 embedding sizes 下进行了实验，对比了标准模型和正则化后的模型的性能变化、信息丰度、以及 optimization dynamics 。结果如 Figure 5 所示。正如预期的那样，DCNv2 中的正则化有助于学习具有更高信息丰度的 embeddings。然而，模型出现了出乎意料的结果：即使 embedding collapse 得到缓解，scalability 也没有提升，甚至有所恶化。研究发现，正则化后的模型在学习过程中会发生过拟合，表现为 training loss 持续下降而 validation AUC 下降。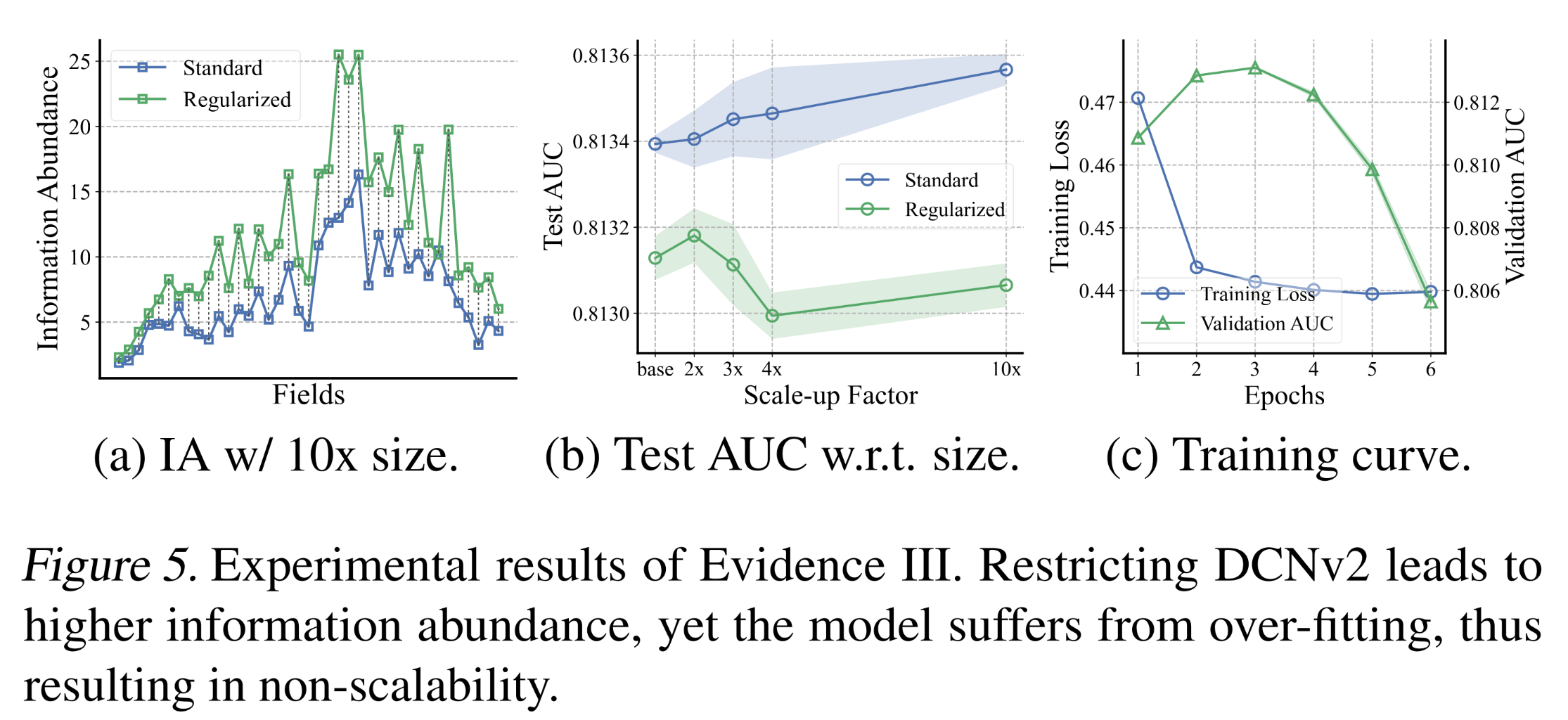

   

3. Evidence IV: Directly avoiding explicit interaction：现在，我们研究直接抑制 feature interaction 对scalability的影响。我们以 DNN 为例——它包含一个简单的 interaction 模块，将来自不同 fields 的所有 feature vectors 拼接起来，并用 MLP进行处理。由于 DNN 不进行显式的二阶 feature interaction ，根据我们之前的 interaction-collapse theory，它受到的 embedding collapse 影响应该较小。我们对比了 DCNv2 和 DNN 学到的 embeddings 、以及它们的性能随 embedding size 增长的变化。考虑到不同架构或目标函数在建模方面可能存在差异，我们主要讨论性能趋势以进行公平比较。结果如 Figure 6 所示。

   • DNN 学到的 embedding matrices 的 collapse 程度较低，表现为信息丰度高于 DCNv2。

   • 然而，事与愿违的是，当增加 embedding size 时，DNN 的 AUC 反而下降。

   这一观察结果表明，尽管 DNN 受到的embedding collapse 影响较小，但它仍然存在过拟合问题，且缺乏 scalability。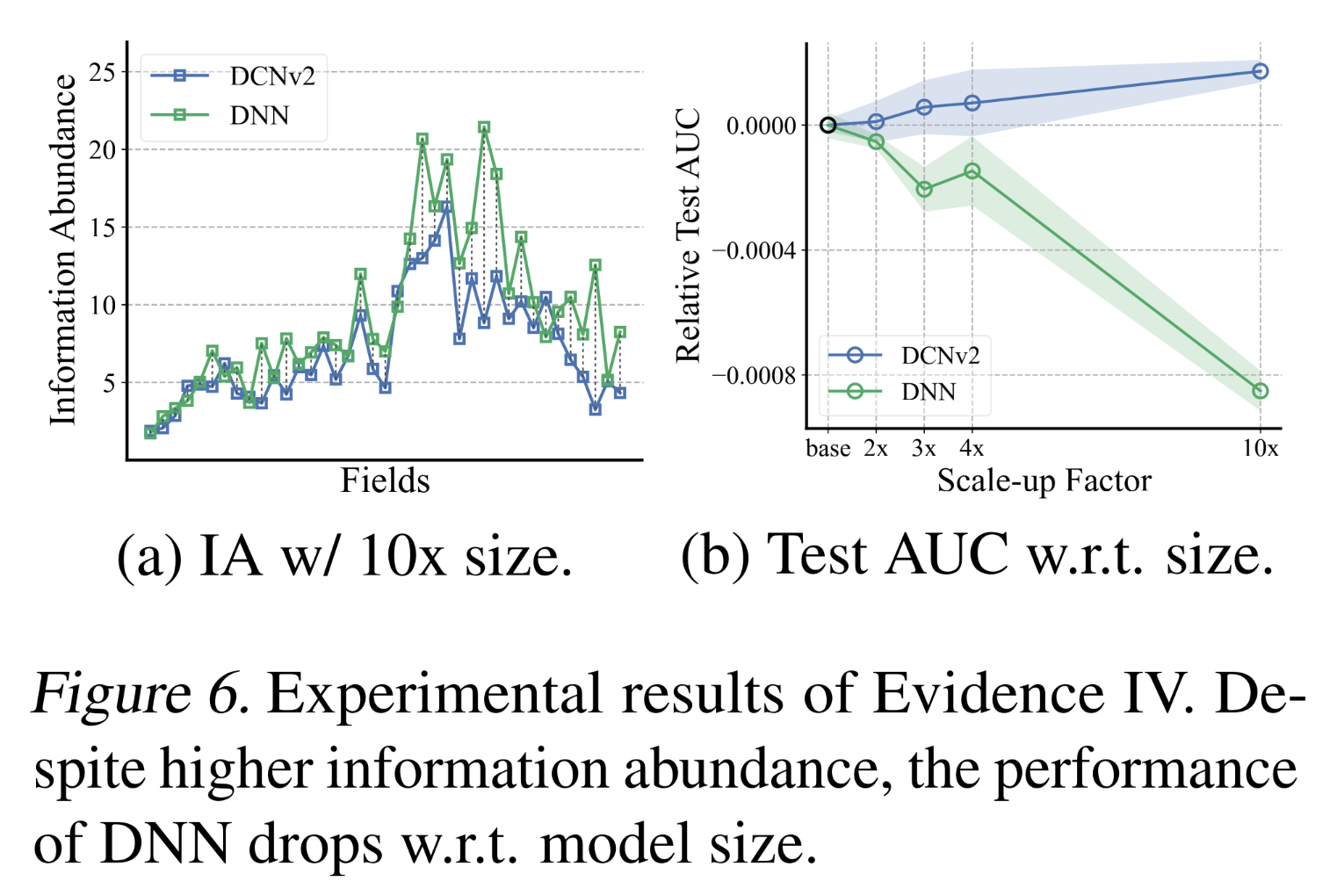

   

4. Summary: Does suppressing collapse definitely improve scalability?：Regularized DCNv2 和 DNN 都是 feature interaction 被抑制的模型——正如预期的那样，它们学到的 embedding matrices 的 collapse 程度低于 DCNv2。然而， evidence III&IV 中的观察结果表明，Regularized DCNv2 和 DNN 都无法随着模型规模的增长而在 AUC 上实现提升，并且都存在严重的过拟合问题。我们得出以下发现：

   • Finding 2：由于过拟合问题，通过不恰当地抑制 feature interaction 而获得的 a less-collapsed model 不足以实现 scalability。

   这一 finding 是合理的，因为feature interaction 融入了推荐系统中 higher-order correlations 的 domain knowledge，有助于形成具有泛化能力的 representations。当 feature interaction 被抑制时，随着 embedding size 的增加，模型往往会拟合噪声，导致泛化能力下降。

1.5 Multi-Embedding Design

1. 在本节中，我们提出了一种简单的 multi-embedding design ——它是一种适用于多种推荐模型架构的有效的 scaling 机制。我们将介绍其整体架构、展示实验结果，并分析 multi-embedding 的工作原理。我们还将讨论 data 的作用，从而为 multi-embedding 提供全面的分析。

1.5.1 Multi-Embedding

1. feature interaction 对 scalability 的 two-sided effect 为 model design 提供了一个核心原则：即 a scalable model 应能够在现有 feature interaction 框架内学习 less-collapsed embeddings ，而不是移除 interaction 。基于这一原则，我们提出了 multi-embedding: ME 作为一种简单而高效的设计，以提升模型 scalability 。

   具体来说，我们通过增加 independent and complete embedding sets 的数量（而非 embedding size ），并融合 embedding-set-specific feature interaction 模块。与 group convolution（《Imagenet classification with deep convolutional neural networks》）、multi-head attention（《Attention is all you need》）、以及推荐系统中其他 decoupling-based 的工作类似，这种设计允许模型联合学习不同的 interaction patterns，从而得到具有 large diversity 的 embedding sets 。而 a single-embedding model 在 pattern extraction 方面受到限制，容易遭受严重的 embedding collapse 。通过 multi-embedding，模型在保留原始 interaction 模块的同时，受到 interaction-collapse theory 的影响较小，从而缓解了 embedding collapse。形式化地，具有 $M$$M$ 个 embedding sets 的推荐模型定义为：

   $$\begin{array}{c}{\overrightarrow{\mathbf{e}}}_i^{(m)}={\left({\mathbf{E}}_i^{(m)}\right)}^{\mathrm{\top }}{\overrightarrow{\mathbf{1}}}_{x_i},\mathrm{\forall }i\in \{1,2,\cdots ,N\},m\in \{1,2,\cdots ,M\}\\ {\overrightarrow{\mathbf{h}}}^{(m)}=I^{(m)}({\overrightarrow{\mathbf{e}}}_1^{(m)},{\overrightarrow{\mathbf{e}}}_2^{(m)},\cdots ,{\overrightarrow{\mathbf{e}}}_N^{(m)})\\ \overrightarrow{\mathbf{h}}=\frac{1}{M}\sum _{m=1}^M{\overrightarrow{\mathbf{h}}}^{(m)}\\ \hat{y}=F\left(\overrightarrow{\mathbf{h}}\right)\end{array}$$

   其中： $m$$m$ 表示 embedding set 的 index。

   这里，多个 feature interaction ${\overrightarrow{\mathbf{h}}}^{(m)}$$\mathbf{\vec h}^{(m)}$ 是通过均值池化来融合的。也可以考虑用 gate-based 或者 attention-based 方法来融合，从而考虑不同 interaction 的重要性。

   注意：interaction 的融合发生在 postprocessing 模块 $F(\cdot )$$F(\cdot)$ 之前。

   multi-embedding 的一个关键要求是，interaction 模块 $I$$I$ 中应包含非线性（如 ReLU）。否则，模型将等价于 single-embedding，无法捕获不同的模式。作为解决方案，我们在具有线性 interaction 模块的模型的 interaction 之后添加一个非线性投影，并减少 postprocessing 模块 $F$$F$ 中的一个 MLP 层，以实现公平比较。single-embedding models 和 mult-embedding models 的整体架构对比如 Figure 7 所示。

   对于 multi-head attention 网络，multi-head 本身就起到了 multi-embedding 的作用。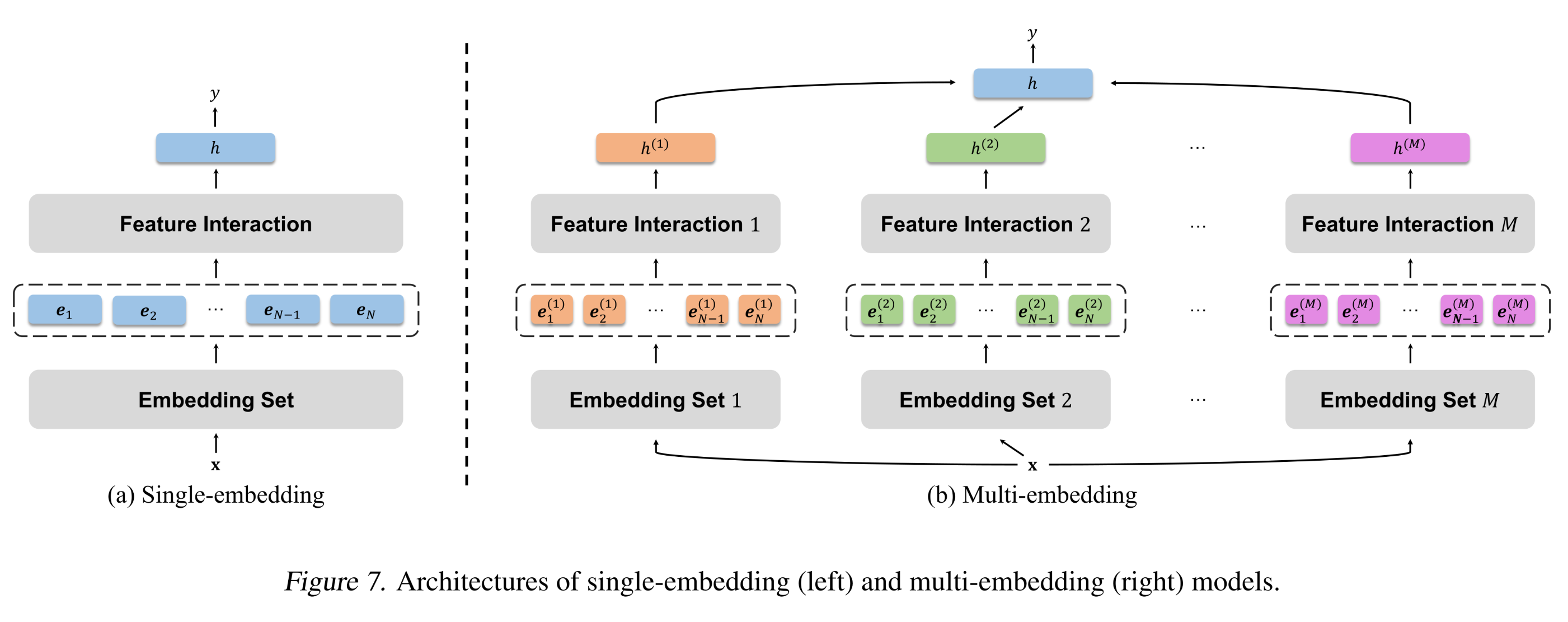

   

1.5.2 实验

1. 数据集：我们在两个推荐系统基准数据集上进行了实验：Criteo 和 Avazu 。这两个数据集规模庞大、具有挑战性，被广泛用于推荐系统研究。

2. baseline 方法：包括 DNN、IPNN、NFwFM、xDeepFM、DCNv2、FinalMLP 、以及它们对应的 multi-embedding 变体（模型规模为 2 倍、3 倍、4 倍和 10 倍）。其中，NFwFM 是 NFM的一个变体，它用 FwFM 替换了 FM。

   所有实验均采用 8/1/1 的 training/validation/test splits，并基于 validation AUC 进行 early stopping。更多细节见附录 C.2。

3. 实验结果：我们每个实验重复 3 次，并报告不同 scaling factors 下的平均 test AUC。结果如 Table 1 所示。

   • 对于 single-embedding 模型，我们观察到所有模型都表现出较差的 scalability ：

     • 只有 DCNv2 和 NFwFM 随着 embedding size 的增加表现出轻微的性能提升（Criteo/Avazu上分别提升 0.00036/0.00093）。

     • 而对于高度依赖 non-explicit interaction 的 DNN、xDeepFM 和 FinalMLP，当规模扩大到 10 倍时，性能甚至下降（Criteo 上下降 0.00136，Avazu 上下降 0.00118）。这与 1.4.2 章节中的讨论一致。

   • 相比之下，我们的 multi-embedding 随着 embedding size 的增长表现出持续且显著的性能提升，并且在最大的 10 倍规模下始终取得最佳性能。

     • 对于 DCNv2 和 NFwFM， multi-embedding 在 Criteo上通过扩大到 10 倍实现了 0.00099 的性能提升、在 Avazu 上实现了 0.00223 的性能提升。这是 single-embedding 无法实现的。

     • 在所有模型和数据集上，与 baselines 相比，最大规模的 multi-embedding 模型平均在 test AUC 上实现了 0.00110 的提升。

   multi-embedding 为突破现有模型的 non-scalability 限制提供了一种有效方法。Figure 8a 可视化了 multi-embedding 在 Criteo 数据集上的 scalability。标准差和详细的 scalability 对比见附录 C.3。

   根据实验结果来看，直接扩大 embedding 参数似乎带来的提升都很微弱，即使是采用 MultiEmbed。但是，采用 MultiEmbed 的效果要比 SingleEmbed 更好，这有利于 embed size 的超参数调优。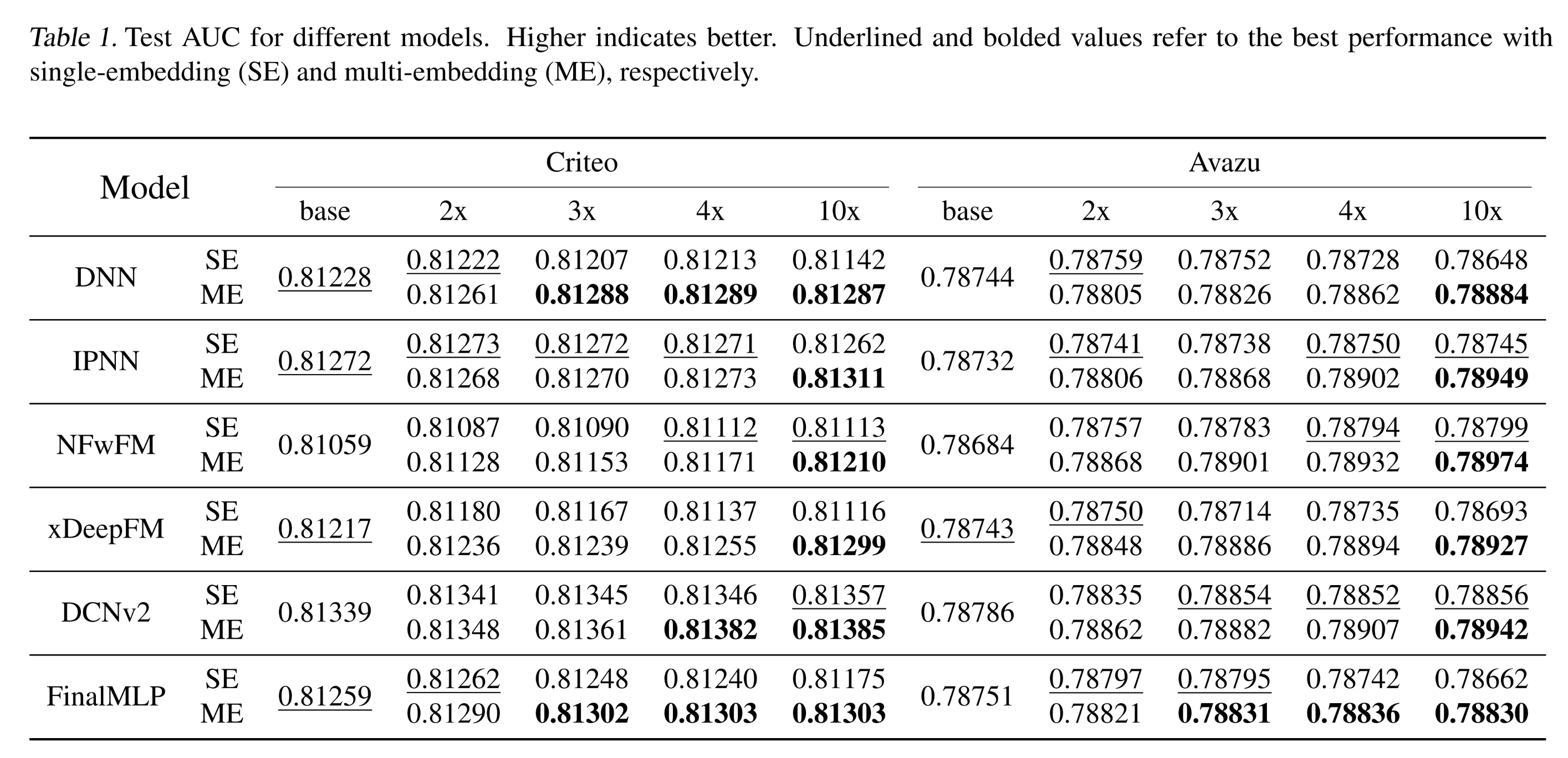

   

   

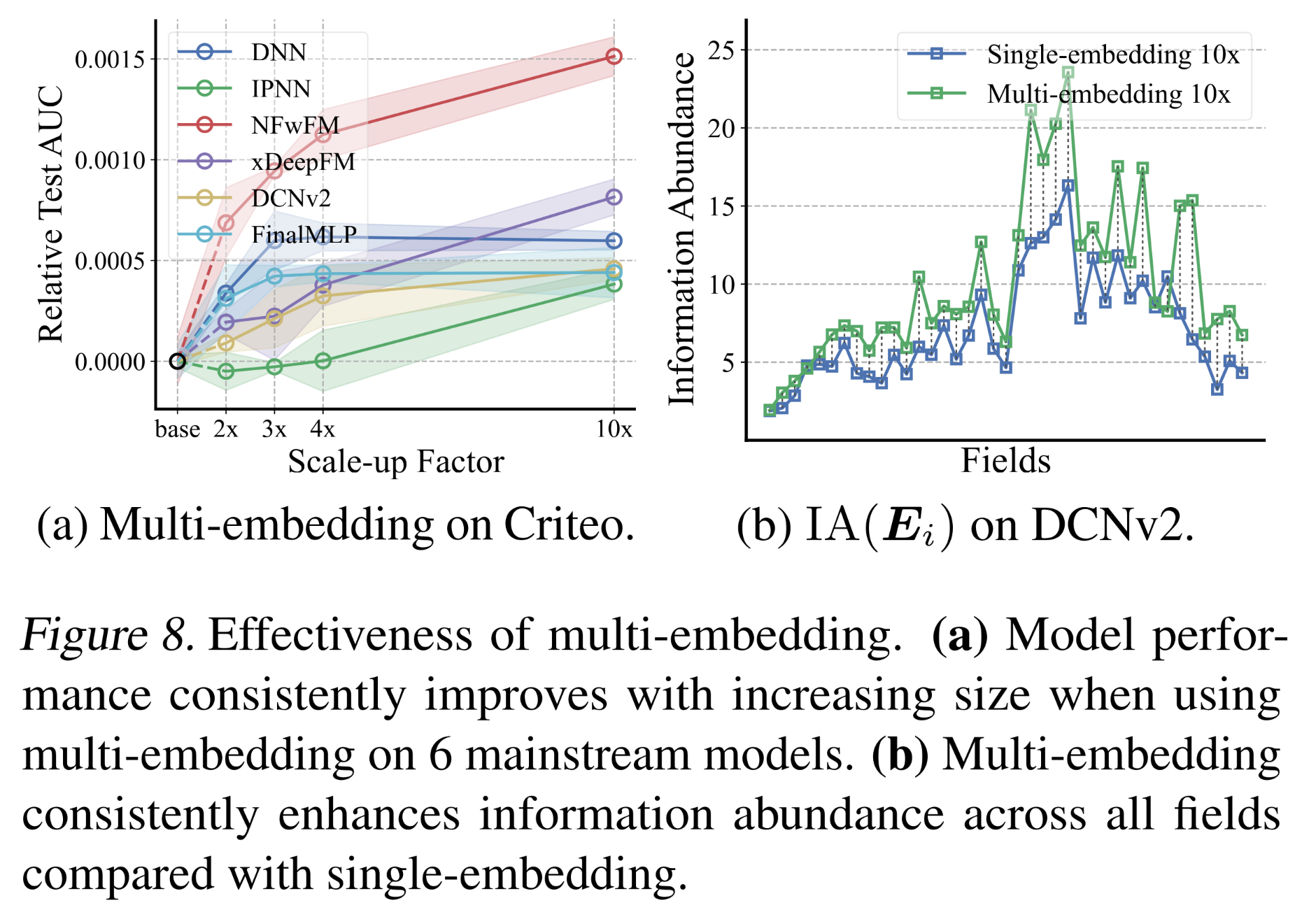
4. embedding collapse 的缓解：为了衡量 mitigation of collapse ，我们对比了 single-embedding DCNv2 和 multi-embedding DCNv2 （最大 10x embedding size ）的信息丰度。为了计算multi-embedding DCNv2 的信息丰度，我们将 multi-embedding DCNv2 中 a single field 的所有 embeddings 拼接在一起，作为这个 field 的 overall embedding。结果如 Figure 8b 所示。可以观察到，与 single-embedding DCNv2 相比，multi-embedding DCNv2 一致地提高了所有 fields 的信息丰度，尤其是对于 fields with larger cardinality。

   这些结果表明，multi-embedding 是一种简单而有效的方法，能够在不引入大量计算资源或超参数的情况下，缓解 embedding collapse 并获得 scalability gain。

5. Deployment in the online system：经过 2023 年 1 月的 online A/B testing，multi-embedding 范式已成功部署于腾讯在线广告平台（全球最大的广告推荐系统之一）。将微信朋友圈（WeChat Moments）的 click prediction model 从 single-embedding 升级为我们提出的 multi-embedding 范式后，商品交易总额（Gross Merchandise Value: GMV）提升了 3.9% ——这意味着每年带来数亿美元的收入增长。

1.5.3 Multi-Embedding 工作原理

1. 受 interaction-collapse theory 的影响较小：根据我们之前的 interaction-collapse theory 和相应分析，embedding collapse 是由不同 fields 之间的 feature interaction 引起的，具体表现为对 sub-embeddings 信息丰度的共同影响。我们证明了 multi-embedding 受这种影响较小。回顾 1.4 节，我们通过计算 $\sum _{i=1}^N\text{IA}\left({\mathbf{E}}_i^{\to j}\right)$$\sum_{i=1}^{N} \text{IA}\left(\mathbf E_{i}^{\to j}\right)$ 来比较 $\text{IA}\left({\mathbf{E}}_i^{\to j}\right)$$\text{IA}\left(\mathbf E_{i}^{\to j}\right)$ 如何受到 the field to interact with 的影响。在这里，我们相应地可视化了 multi-embedding DCNv2 和 single-embedding DCNv2 的结果，如 Figure 9 所示。可以观察到，multi-embedding 中的相关系数显著小于 single-embedding（0.52 对比 0.68）。因此，信息丰度受 the field to interact with 的影响较小，从而减轻了 interaction-collapse theory 的影响。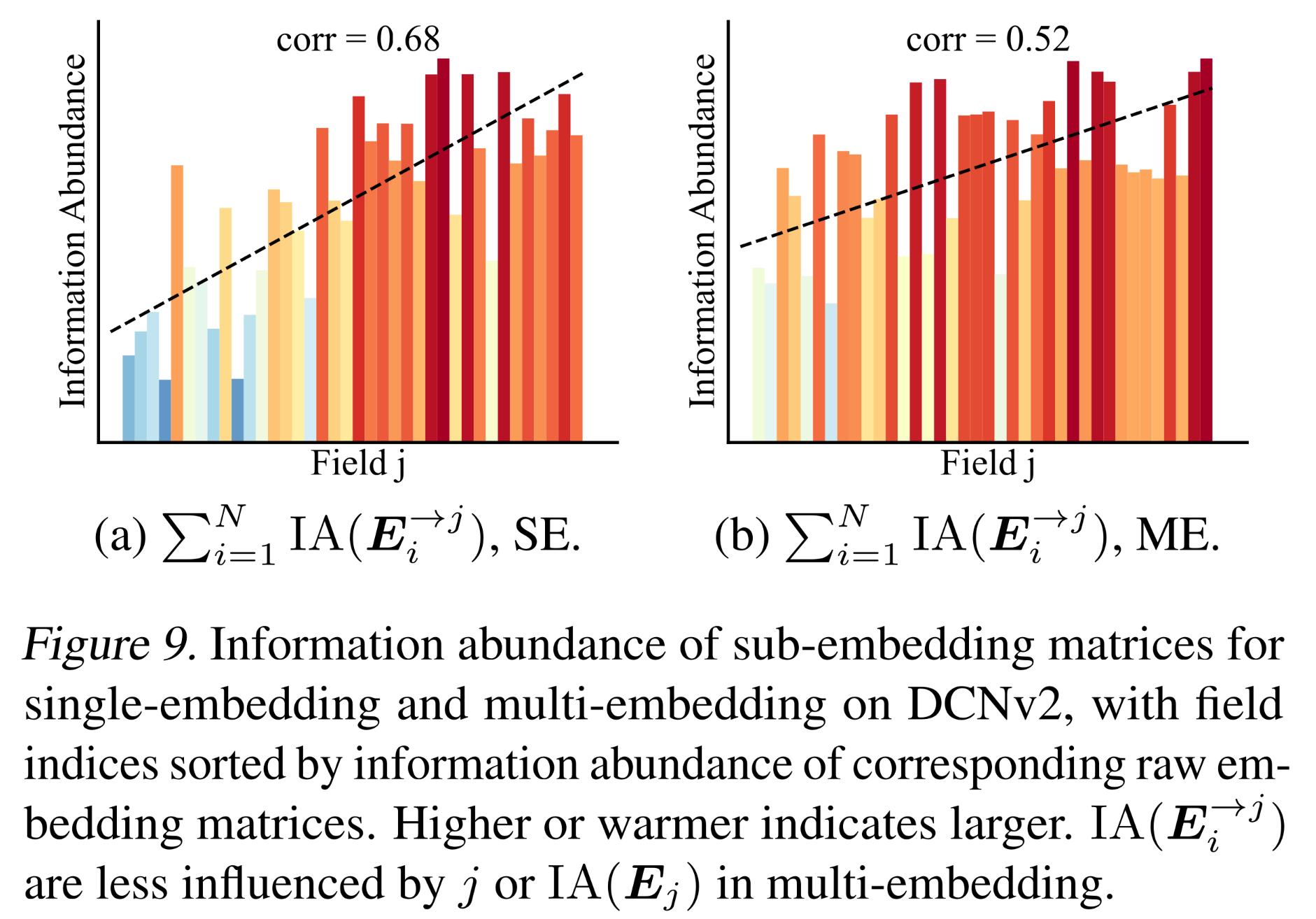

   

2. 通过 embedding diversity 缓解 embedding collapse：我们进一步证明，multi-embedding 通过允许 diversity of embedding sets 来缓解 embedding collapse。为说明这一点，我们引入主角度（principal angle）的余弦 $\cos \left({\varphi }_i^{m\leftrightarrow m^{\prime }}\right)$$\cos\left(\phi_{i}^{m \leftrightarrow m^\prime}\right)$ 来衡量任意特定 field $i$$i$ 的 a pair of embedding sets $m$$m$ 和 $m^{\prime }$$m^\prime$ 之间的空间相似性（space similarity ）：通过以下进一步的奇异值分解计算：

   $${\left({\mathbf{U}}_i^{(m)}\right)}^{\mathrm{\top }}{\mathbf{U}}_i^{(m^{\prime })}={\mathbf{P}}_i^{(m)}\text{diag}(\cos \left({\varphi }_i^{m\leftrightarrow m^{\prime }}\right)){\left({\mathbf{P}}_i^{(m^{\prime })}\right)}^{\mathrm{\top }}$$

   低秩的 ${\left({\mathbf{U}}_i^{(m)}\right)}^{\mathrm{\top }}{\mathbf{U}}_i^{(m^{\prime })}$$\left(\mathbf U_i^{(m)}\right)^\top \mathbf U_i^{(m^\prime)}$ 意味着 overall embedding $[{\mathbf{E}}_i^{(m)},{\mathbf{E}}_i^{(m^{\prime })}]$$\left[\mathbf E_{i}^{(m)}, \mathbf E_{i}^{(m^\prime)}\right]$ 是高秩的。因此，我们引入一个广义度量：

   $$\text{div}({\mathbf{E}}_i^{(m)},{\mathbf{E}}_i^{(m^{\prime })})=1-\frac{1}{K}{\Vert \cos \left({\varphi }_i^{m\leftrightarrow m^{\prime }}\right)\Vert }_1$$

   来描述 diversity of embedding sets。多样性越大，表明 overall embedding 的信息丰度越高，或 embedding collapse 的缓解效果越好。

   为进行对比，我们分别将 embedding of a single-embedding DCNv2 和 ideal random-initialized matrix 分割为 embedding sets ，并与 multi-embedding DCNv2 进行比较。 Figure 10a 展示了所有 embedding set pairs 和所有 fields 的平均多样性。结果表明，与 single-embedding 相比，multi-embedding 能够显著降低 embedding set similarity ，从而缓解 embedding collapse。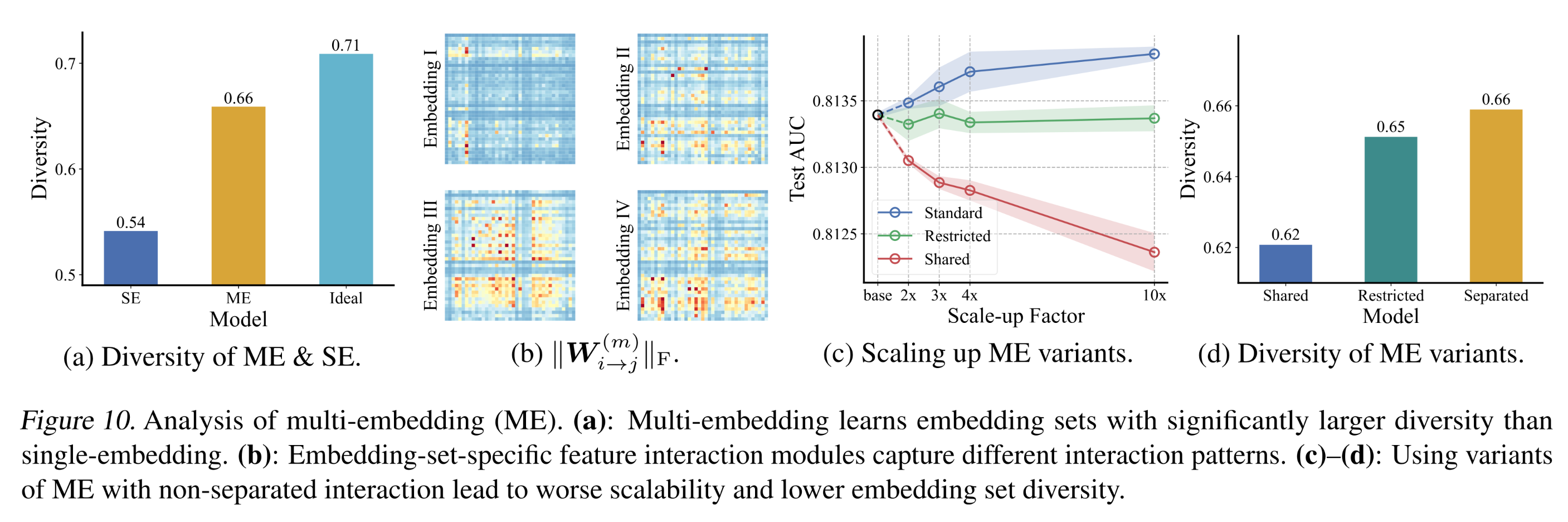

   

3. 从 separated interaction 中获得 diversity：我们进一步证明，multi-embedding 模型的 embedding diversity 源于 embedding-set-specific feature interaction 模块——这允许 embedding sets 捕获 diverse interaction patterns 。

   • 一方面，我们在 Figure 10b 中可视化了 multi-embedding DCNv2 模型的 ${\Vert {\mathbf{W}}_{i\to j}^{(m)}\Vert }_F$$\left\| \mathbf W_{i \to j}^{(m)} \right\|_{F}$作为 interaction pattern （《DCN V2: Improved Deep & Cross Network and Practical Lessons for Web-scale Learning to Rank Systems》）。结果表明，interaction 模块学习到了多样化的模式。

   • 另一方面，我们将 multi-embedding 与两种具有 non-separated interaction 的变体进行了比较：

     • (a)：所有 feature interaction 模块在所有 embedding sets 之间共享。

     • (b)：通过正则化来限制所有 embedding sets 之间 ${\Vert {\mathbf{W}}_{i\to j}^{(m)}\Vert }_F$$\left\| \mathbf W_{i \to j}^{(m)} \right\|_{F}$ 的差异。

     结果如 Figure 10c 和 Figure 10d 所示。与 multi-embedding 中的 separated design 相比，这两种 feature interaction design 变体表现出更差的 scalability 和 embedding diversity ，表明 multi-embedding 的有效性源于 separation of interaction modules。

1.5.4 Data 在 Embedding Collapse 中的作用

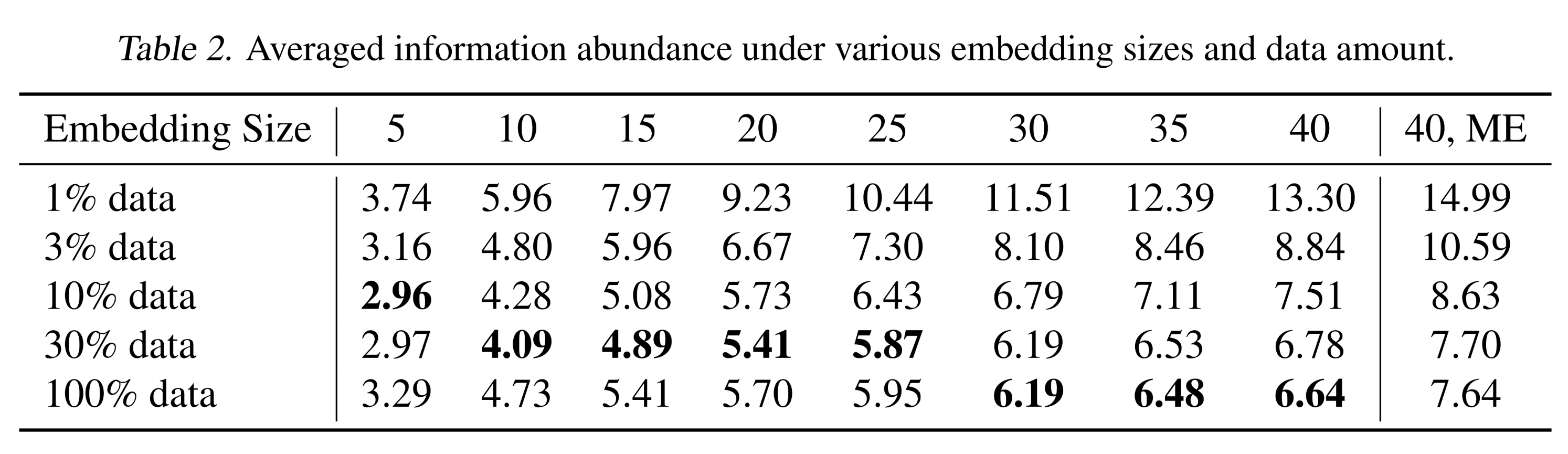
1. 在本文中，我们主要关注 model scalability ，并指出了推荐模型的固有问题—— embedding collapse。我们实验中 benchmark datasets 的海量数据量，为 embedding collapse 现象提供了与数据量无关的可信度。在本节中，我们进一步讨论 embedding collapse 现象在不同数据量下的表现。为说明这一点，我们使用 Criteo 数据集的不同规模子集进行了额外实验。我们测量了不同 model scales 下 embedding 矩阵的平均信息丰度，结果总结于 Table 2。

   从结果可以观察到，数据规模确实会影响 embedding 矩阵的信息丰度，但信息丰度并不会随着数据规模的增加而严格增加，甚至可能下降（尤其是对于较大的模型）。这一发现背后的原因是，embedding collapse 由两个方面决定：

   • (1)：数据规模，会增加信息丰度。

   • (2)：interaction-collapse law，会降低信息丰度。

   在给定 embed size 的情况下，数据量越多，信息丰度越低。这代表了 embedding matrix 拟合数据的结果。这通常是由于 feature interaction 的影响，因为更多的数据包含了更多的 interaction。

   在所有结果中：

   • 只有当数据规模为 10%∼100% 且 embedding size = 5、或数据规模为 30%∼100% 且 embedding size in (10, 15, 20, 25) 时，我们观察到 embedding collapse 是由 limited data 导致的。

   • 而在大多数其他情况下，异常的下降趋势表明embedding collapse 是由 interaction-collapse law 而非 limited data 导致的。

   • 此外，multi-embedding 在不同数据量下都一致地优于 single-embedding ，表明我们提出的 multi-embedding design 具有普适性。

   

1.6 结论

1. 在本文中，我们指出了现有推荐模型的 non-scalability 问题，并确定了阻碍 scalability 的 embedding collapse 现象。通过围绕 embedding collapse 的实证分析和理论分析，我们得出了 feature interaction 对 scalability 的 two-sided effect：即 feature interaction 会导致embedding collapse ，但同时减少过拟合。我们提出了一种统一的 multi-embedding design ，在不抑制 feature interaction 的前提下缓解 embedding collapse 。benchmark datasets 上的实验表明，multi-embedding 能够一致地提升模型 scalability，并有效缓解 embedding collapse 。

二、附录

2.1 Embedding 的重要性 (Appendix A)

1. 对于推荐模型，embedding 模块占据了参数量的最大部分（对于 Criteo 数据集，在我们的 DCNv2 baseline 中超过 92%；在工业模型中的比例更高），因此是模型中重要且关键的 bottleneck 部分。为进一步说明，我们讨论了推荐模型其他模块的 scaling up ——即 feature interaction 模块 $I$$I$ 和 postprocessing prediction 模块 $F$$F$。我们通过实验增加了 DCNv2 baseline 中的 #cross layers 和 #MLP layers，并在 Table 3 中展示了结果。

   可以观察到，增加 #cross layers 或 #MLP layers 并不会带来性能提升，因此扩大 embedding size 是合理且必要的。

   

2.2 讨论：语言模型中的 Embeddings (Appendix B)

1. 为了将分析扩展到其他模型，我们考察了 pretrained T5 模型，并评估了其（归一化的）奇异值以进行比较。结果如 Figure 11 所示。观察发现，T5 与 DCNv2 相比：

   • (1)：保持了更高的归一化奇异值（normalized singular values）。

   • (2)：尽管其 embedding size 更大，但其极小奇异值的比例更低。

   这些观察结果表明，T5 对 embedding collapse 现象的敏感性较低，这可能是因为 text-based models 受 field interactions 的 interaction-collapse law 的影响较小；而 field interactions 是导致 embedding collapse 的原因。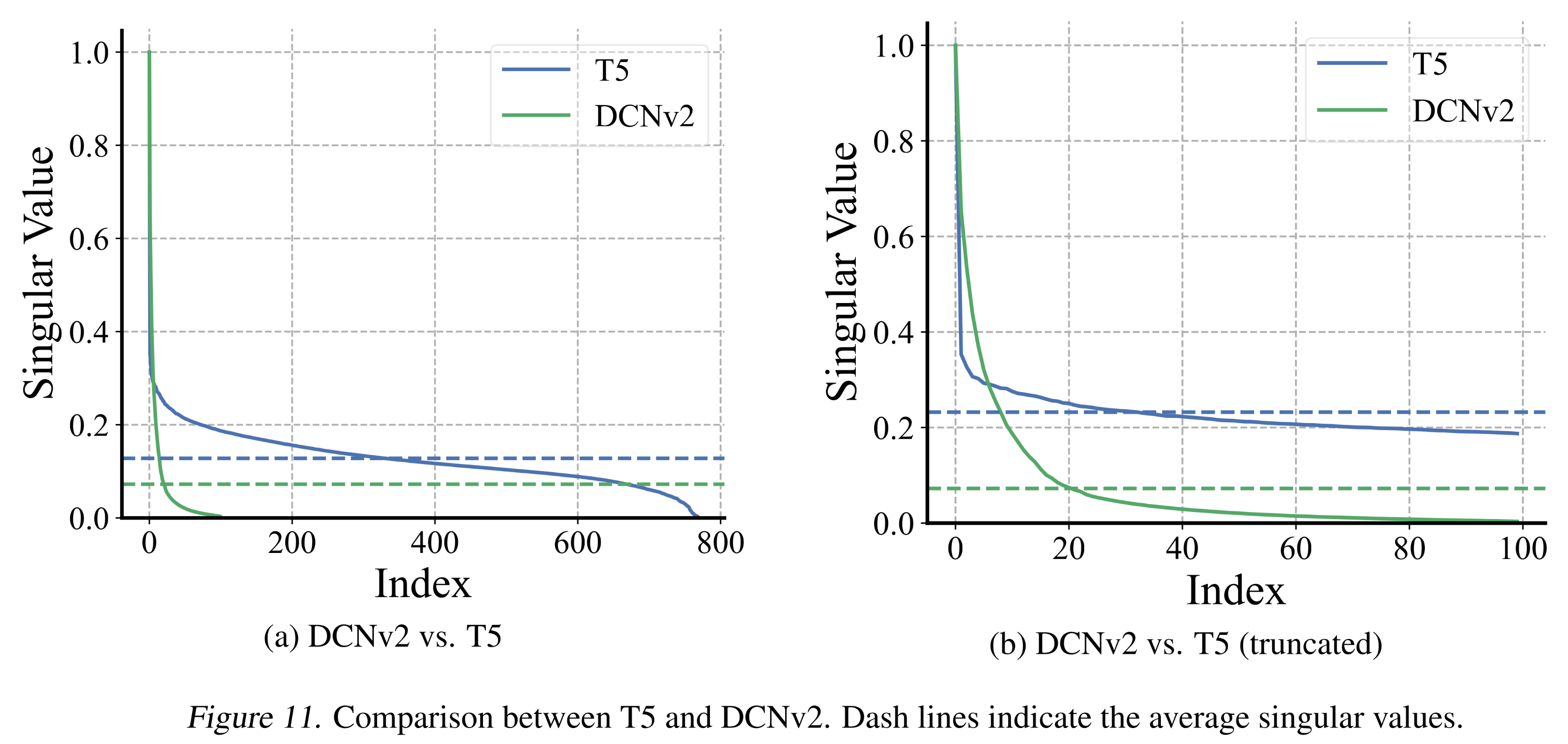

   

2.3 实验细节 (Appendix C)

1. 数据集（Appendix C.1）：Criteo 和 Avazu 的统计信息如 Table 4 所示。可以看出，数据量充足，且 $D_i$$D_{i}$ 的变化范围很大。

   

2. 实验配置（Appendix C.2）：

   • Specific multi-embedding design：

     • 对于 DCNv2、DNN、IPNN 和 NFwFM，我们分别在 the stacked cross layers、 the concatenation layer 、the inner product layer 和 the field-weighted dot product layer 之后添加一个非线性投影。

     • 对于 xDeepFM，我们直接对 compressed interaction network 的输出进行平均，并以与 pure DNN model 相同的方式处理the ensembled DNN 。

     • 对于 FinalMLP，我们分别对 two-stream outputs 进行平均。

   • 超参数：

     • 所有实验均使用 random seed 0 将数据集按 8:1:1 分割为 training/validation/test。

     • 我们使用 Adam optimizer， batch size = 2048，学习率为 0.001，weight decay = 1e-6。

     • 对于 base size，考虑到池化操作因此 NFwFM 的 embedding size = 50，其他所有实验的 embedding size 设置为 10。

     • 我们发现 MLP 的 hidden size 和 depth 对结果影响不大；为简化起见，所有模型的 hidden size 均设置为 400，depth 设置为 3（2 hidden layers 和 1 output layer ）。

     • DCNv2 使用 4 cross layers，xDeepFM 的 hidden size 设为 16。

     • 所有实验均基于 validation AUC 进行 early stopping（patience = 3）。

     • 每个实验使用不同的 random initialization 重复 3 次。

     • 所有实验均可在单个 NVIDIA GeForce RTX 3090 上完成。

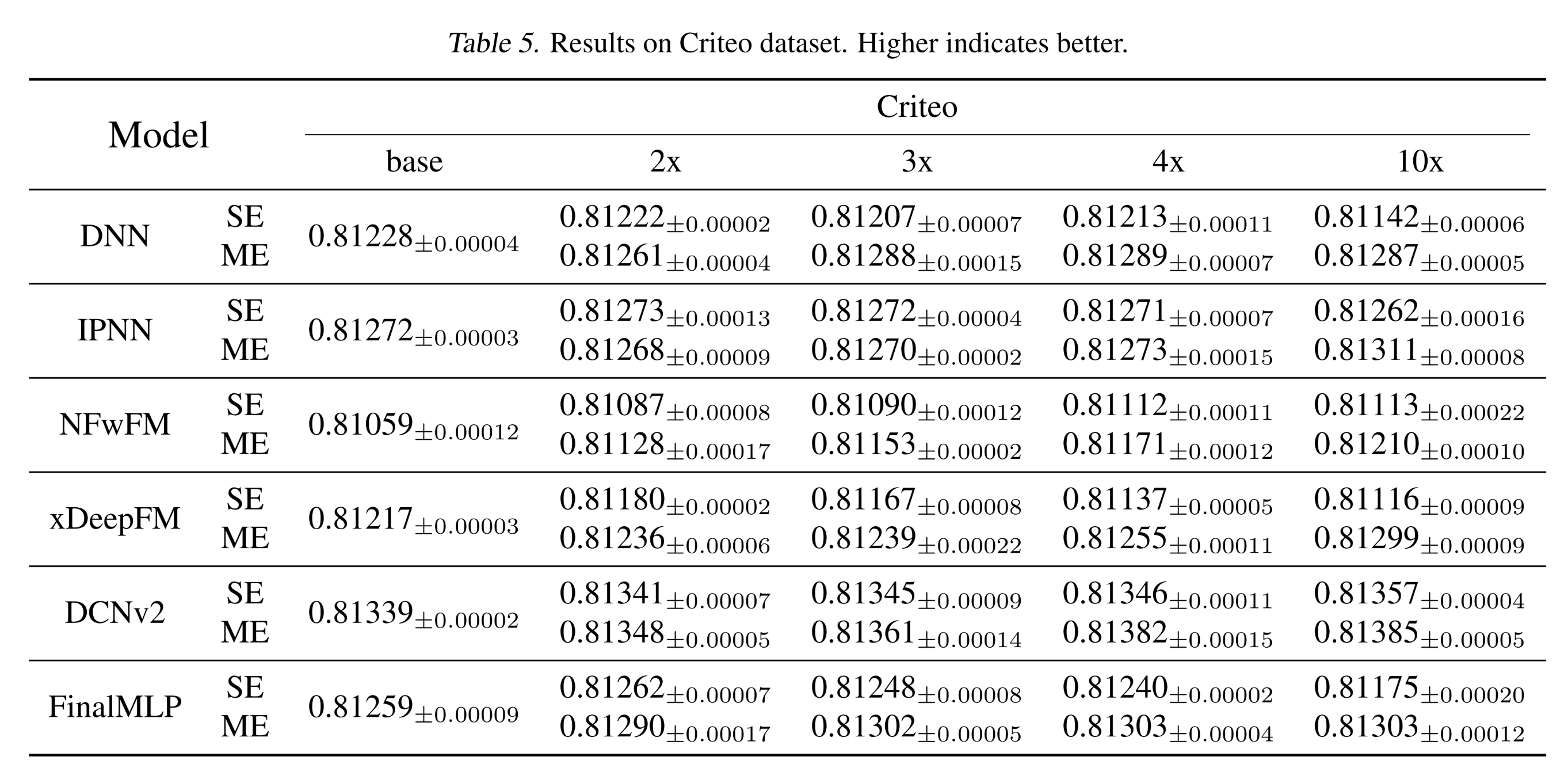
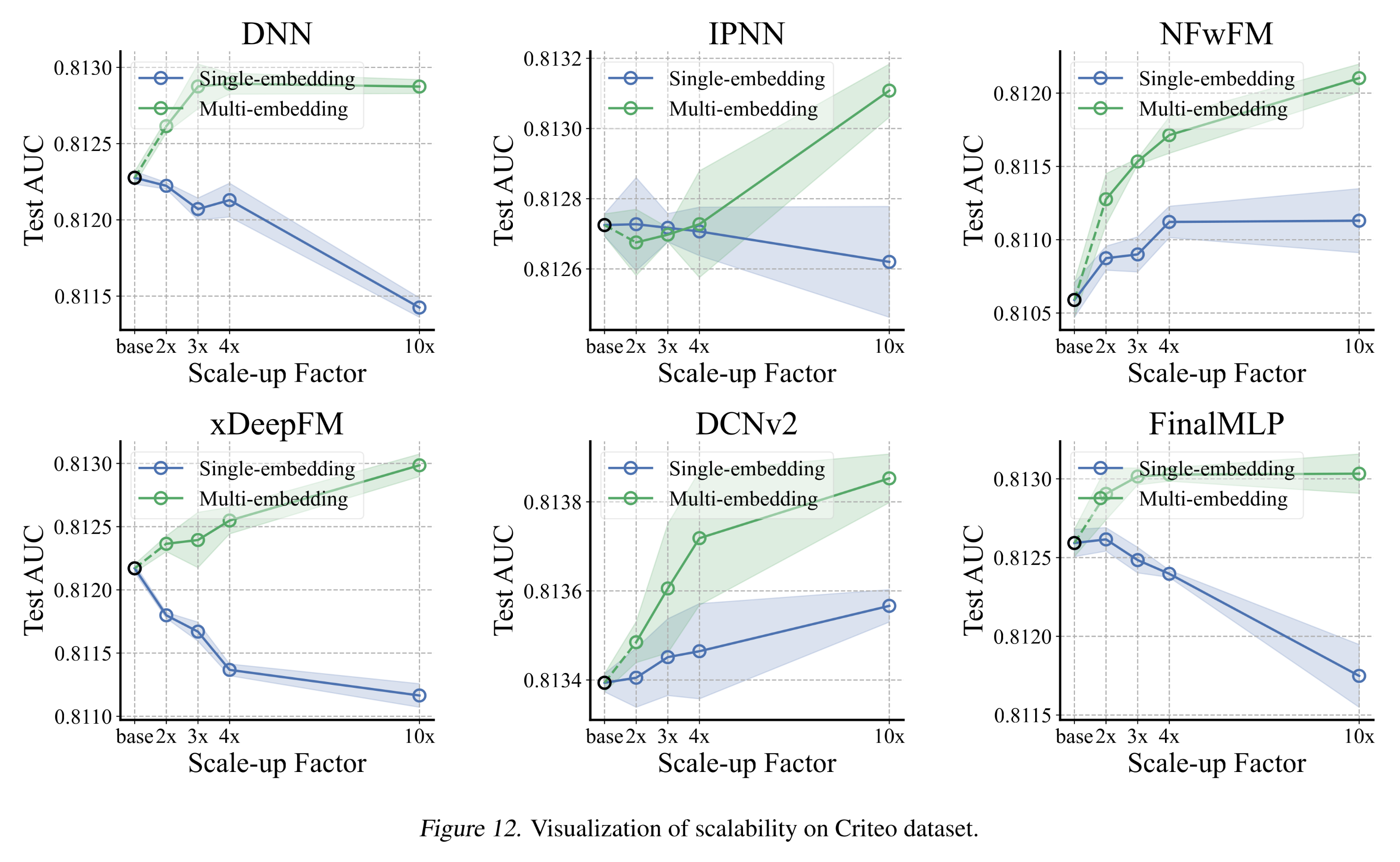
3. 实验结果（Appendix C.3）：此处提供详细的实验结果及 estimated 的标准差。具体来说：

   • Tbale 5 和 Figure 12 展示了 Criteo 数据集上的结果。

   • Table 6 和 Figure 13 展示了 Avazu 数据集上的结果。

   

   

   

   

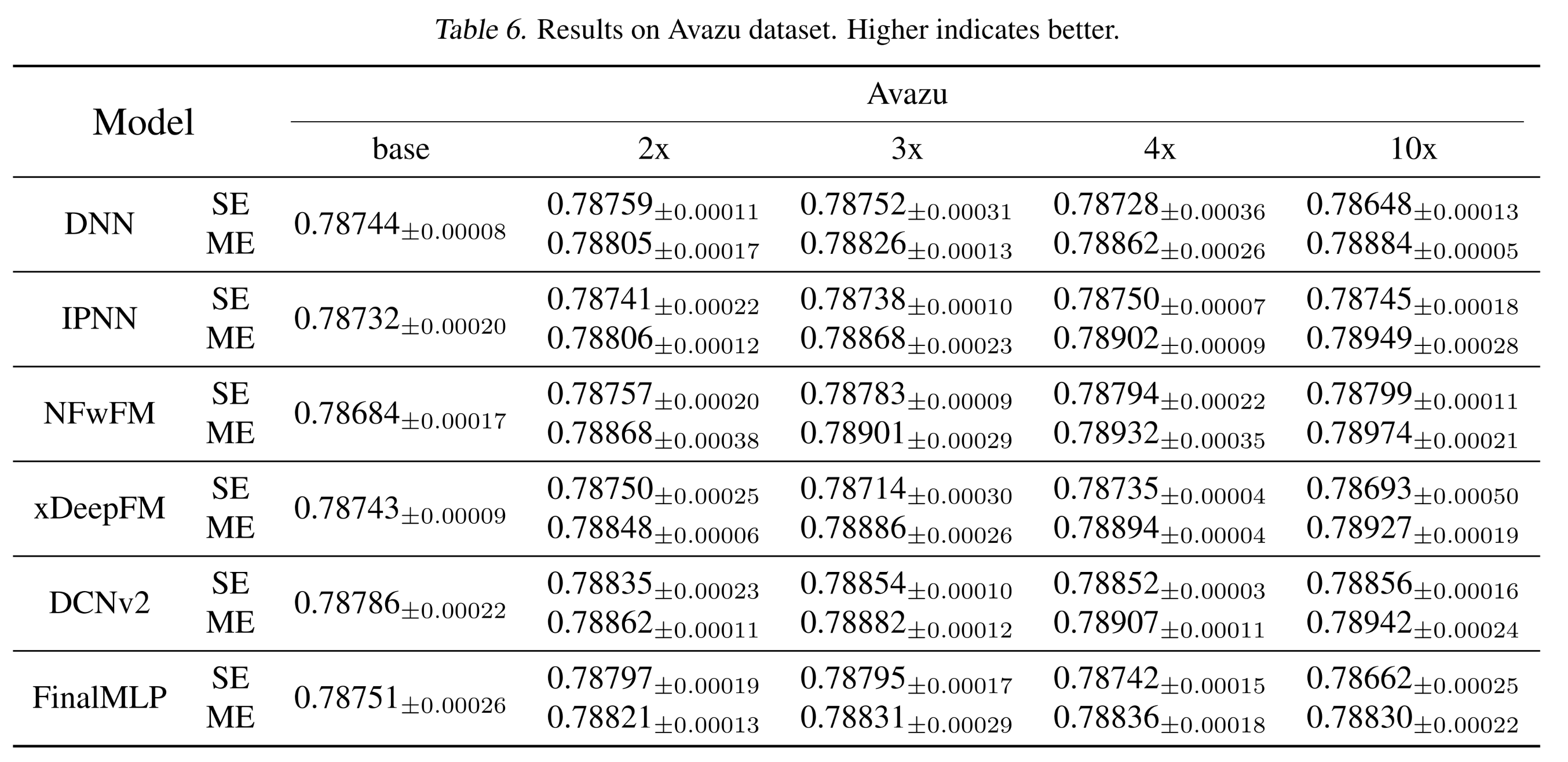
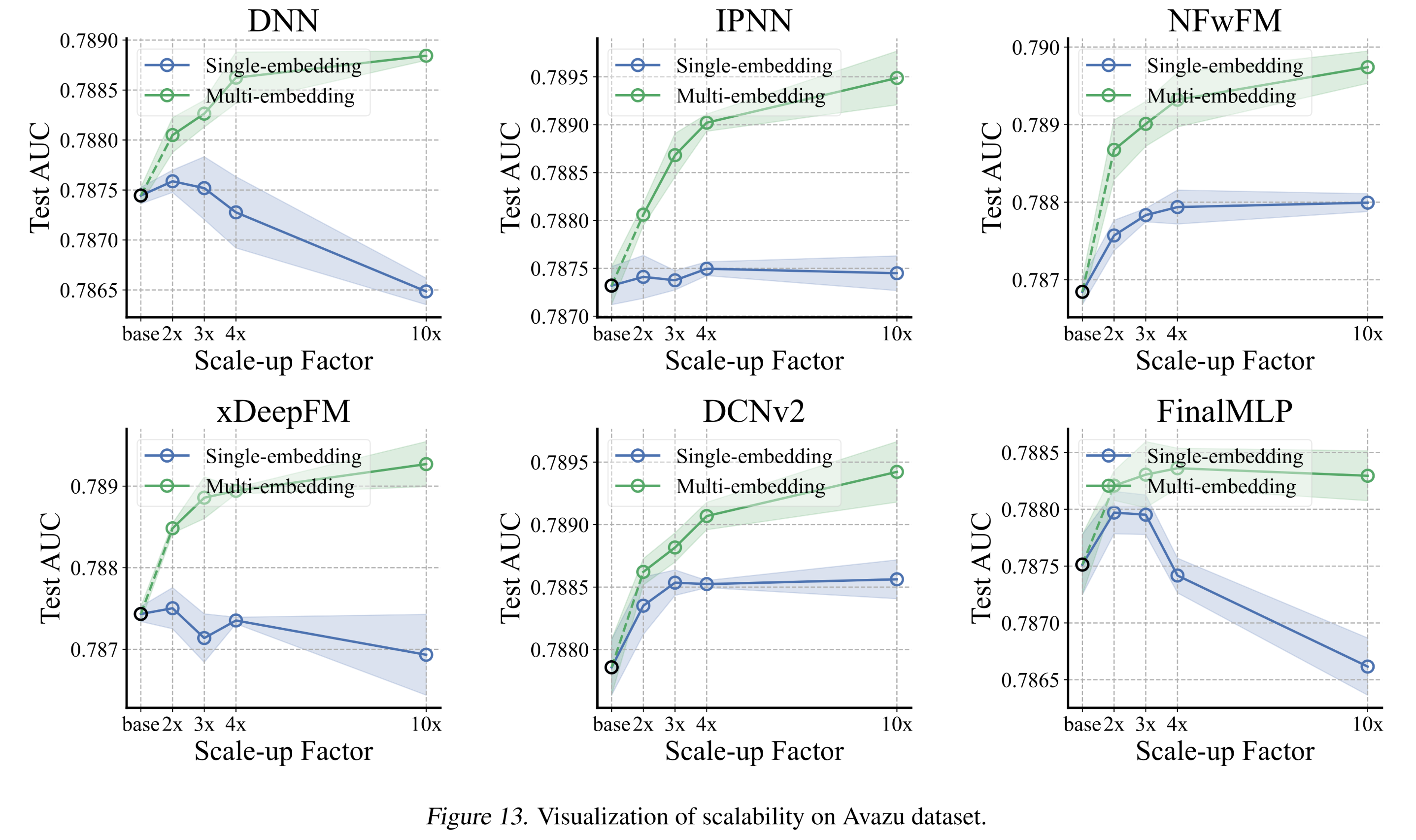
2.4 更多 Baseline 方法 (Appendix D)

1. 我们还在 AutoInt 上进行了实验，对比了 single-embedding 和 multi-embedding 的性能。由于计算资源有限，我们仅在 Criteo 数据集上将模型扩大到 4 倍。结果如 Table 7 所示。可以观察到，single-embedding 存在 non-scalability 的问题，而我们的 multi-embedding 随着模型规模的增长持续提升性能：通过简单地 scaling up 从而实现了 6e-4 的 AUC 提升。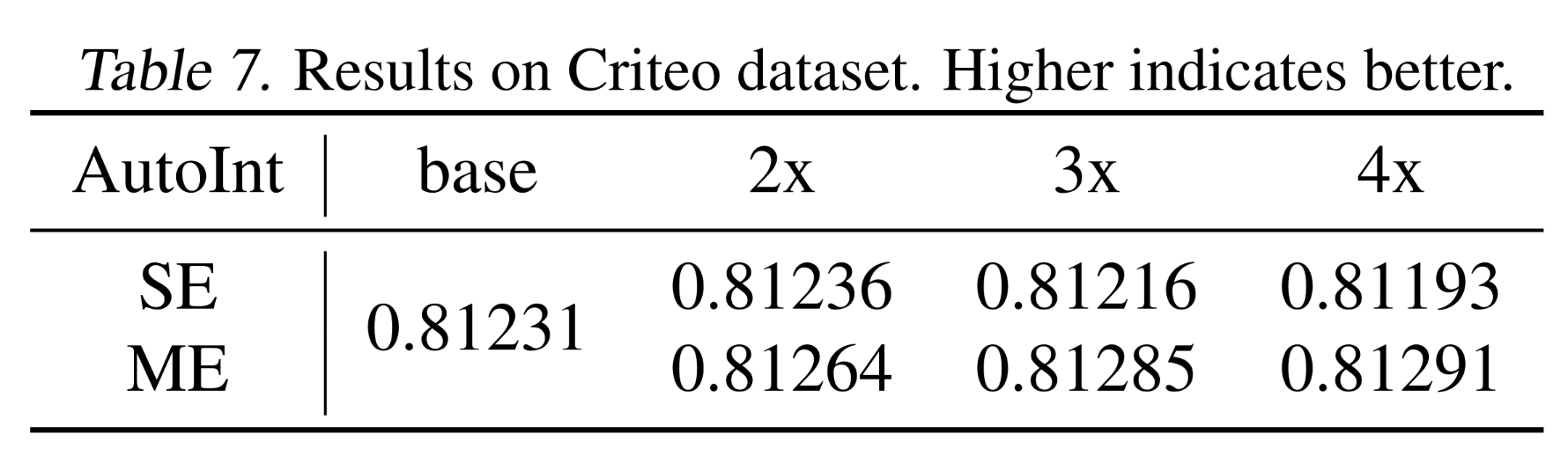

   

2.5 Multi-Embedding 的 Non-Linearity 要求 (Appendix E)

1. 我们之前提到，multi-embedding 的 embedding-set-specific feature interaction 应包含非线性（non-linearity）；否则，模型将退化为 single-embedding 模型。

   为简化起见，我们考虑一种更强版本的 multi-embedding：来自不同 embedding sets 的 combined features 被拼接起来，而不是均值池化。为进一步说明，考虑 linear feature interaction 模块 $I^{(m)}:{\left({\mathbb{R}}^K\right)}^N\to {\mathbb{R}}^h$$I^{(m)}: \left(\mathbb{R}^{K}\right)^{N} \to \mathbb{R}^{h}$，则我们可以定义一个 linear feature interaction 模块 $I_{\text{all}}:{\left({\mathbb{R}}^{MK}\right)}^N\to {\mathbb{R}}^{Mh}$$I_\text{all}: \left(\mathbb{R}^{MK}\right)^{N} \to \mathbb{R}^{Mh}$。为方便起见，我们用 $[f(i){]}_{i=1}^n$$[f(i)]_{i=1}^{n}$ 表示 $[f(1),f(2),\cdots ,f(n)]$$[f(1), f(2), \cdots, f(n)]$，用 ${\overrightarrow{\mathbf{e}}}_i={\left[{\overrightarrow{\mathbf{e}}}_i^{(m)}\right]}_{m=1}^M$$\mathbf{\vec e}_{i} = \left[\mathbf{\vec e}_{i}^{(m)}\right]_{m=1}^{M}$ 表示 $[{\overrightarrow{\mathbf{e}}}_i^{(1)},{\overrightarrow{\mathbf{e}}}_i^{(2)},\cdots ,{\overrightarrow{\mathbf{e}}}_i^{(M)}]$$\left[\mathbf{\vec e}_i^{(1)},\mathbf{\vec e}_i^{(2)},\cdots,\mathbf{\vec e}_i^{(M)}\right]$。$I_{\text{all}}$$I_\text{all}$ 的形式可以表示为：

   $$I_{\text{all}}({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)={\left[I^{(m)}({\overrightarrow{\mathbf{e}}}_1^{(m)},{\overrightarrow{\mathbf{e}}}_2^{(m)},\cdots ,{\overrightarrow{\mathbf{e}}}_N^{(m)})\right]}_{m=1}^M$$

   这表明：a multi-embedding model 等价于 a model by concatenating all embedding sets。我们将进一步证明，所推导出的具有 $I_{\text{all}}$$I_\text{all}$ 的模型与 embedding size = MK 的 single-embedding 模型是同构的：即，对于 linear feature interaction 模块，multi-embedding 与 single-embedding 相似。令 single-embedding 的 feature interaction 模块为 $I$$I$。尽管 $I_{\text{all}}$$I_\text{all}$ 可能与 $I$$I$ 具有不同的形式，我们通过三个例子进一步说明 $I_{\text{all}}$$I_\text{all}$ 和 $I$$I$ 的同构性（homogeneity）。

   • DNN：忽略后续的 MLP，DNN 通过将所有 fields 拼接起来从而包含一个 non-parametric interaction module 。形式化地，我们有：

     $$\begin{array}{c}I({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)={\left[{\left[{\overrightarrow{\mathbf{e}}}_i^{(m)}\right]}_{m=1}^M\right]}_{i=1}^N\\ I_{\text{all}}({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)={\left[{\left[{\overrightarrow{\mathbf{e}}}_i^{(m)}\right]}_{i=1}^N\right]}_{m=1}^M\end{array}$$

     换句话说，$I$$I$ 和 $I_{\text{all}}$$I_\text{all}$ 仅在排列上有所不同，因此 multi-embedding 和 single-embedding 是等价的。

   • Projected DNN：如果我们在 DNN 之后添加一个线性投影（linear projection），则可以将投影针对 fields 和 embedding sets 进行拆分，并推导得到：

     $$\begin{array}{c}I({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)=\sum _{i=1}^N\sum _{m=1}^M{\mathbf{W}}_{i,m}{\overrightarrow{\mathbf{e}}}_i^{(m)}\\ I_{\text{all}}({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)={\left[\sum _{i=1}^N{\mathbf{W}}_{i,m}{\overrightarrow{\mathbf{e}}}_i^{(m)}\right]}_{m=1}^M\end{array}$$

     换句话说，$I$$I$ 和 $I_{\text{all}}$$I_\text{all}$ 仅在求和上有所不同。实际上，如果我们对 $I_{\text{all}}$$I_\text{all}$ 的 combined features 进行平均（而非拼接）以恢复我们所提出的 multi-embedding 版本，则 multi-embedding 乘以标量 $M$$M$ 和 single-embedding 之间是等价的。

   • DCNv2：DCNv2 通过以下方式融合 feature interaction：

     $$I({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)={[{\overrightarrow{\mathbf{e}}}_i\odot \sum _{j=1}^N{\mathbf{W}}_{j\to i}{\overrightarrow{\mathbf{e}}}_j]}_{i=1}^N$$

     因此，通过拆分 ${\mathbf{W}}_{i\to j}$$\mathbf W_{i \to j}$，我们有：

     $$\begin{array}{c}I({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)={\left[{[{\overrightarrow{\mathbf{e}}}_i^{(m)}\odot \sum _{j=1}^N\sum _{m^{\prime }=1}^M{\mathbf{W}}_{j\to i}^{(m,m^{\prime })}{\overrightarrow{\mathbf{e}}}_j^{(m^{\prime })}]}_{m=1}^M\right]}_{i=1}^N\\ I_{\text{all}}({\overrightarrow{\mathbf{e}}}_1,{\overrightarrow{\mathbf{e}}}_2,\cdots ,{\overrightarrow{\mathbf{e}}}_N)={\left[{[{\overrightarrow{\mathbf{e}}}_i^{(m)}\odot \sum _{j=1}^N{\mathbf{W}}_{j\to i}^{(m)}{\overrightarrow{\mathbf{e}}}_j^{(m)}]}_{i=1}^N\right]}_{m=1}^M\end{array}$$

     通过简单地令 ${\mathbf{W}}^{(m,m)}={\mathbf{W}}^{(m)}$$\mathbf W^{(m, m)} = \mathbf W^{(m)}$ ，且当 $m\ne m^{\prime }$$m \neq m'$ 时令 ${\mathbf{W}}^{(m,m^{\prime })}=\mathbf{0}$$\mathbf W^{(m, m')} = \mathbf 0$ （即，全零矩阵），我们可以通过排列（permutation）从而将 multi-embedding 模型转换为 single-embedding 模型。因此，对于 DCNv2，multi-embedding 是 single-embedding 的一个特例。

2. 总结：总之，linear feature interaction module 会导致 single-embedding和 multi-embedding 的同构性。因此，在 feature interaction 模块中使用或引入非线性是必要的。

2.6 Embedding Diversity 的详细解释 (Appendix F)

1. 在 1.5.3 节中，我们提出使用主角度（principal angle）来衡量 embedding set diversity。此处我们介绍其动机和一个示例。注意：

   $$\begin{array}{c}\text{rank}\left([{\mathbf{E}}^{(m)},{\mathbf{E}}^{(m^{\prime })}]\right)=\text{rank}\left([{\mathbf{U}}^{(m)}{\mathbf{\Sigma }}^{(m)}{\left({\mathbf{V}}^{(m)}\right)}^{\mathrm{\top }},{\mathbf{U}}^{(m^{\prime })}{\mathbf{\Sigma }}^{(m^{\prime })}{\left({\mathbf{V}}^{(m^{\prime })}\right)}^{\mathrm{\top }}]\right)\\ =\text{rank}\left([{\mathbf{U}}^{(m)}{\mathbf{\Sigma }}^{(m)}{\left({\mathbf{V}}^{(m)}\right)}^{\mathrm{\top }},{\mathbf{U}}^{(m^{\prime })}{\mathbf{\Sigma }}^{(m^{\prime })}{\left({\mathbf{V}}^{(m^{\prime })}\right)}^{\mathrm{\top }}]\left[\begin{array}{cc}{\mathbf{V}}^{(m)}& \mathbf{0}\\ \mathbf{0}& {\mathbf{V}}^{(m^{\prime })}\end{array}\right]\right)\\ =\text{rank}\left([{\mathbf{U}}^{(m)}{\mathbf{\Sigma }}^{(m)},{\mathbf{U}}^{(m^{\prime })}{\mathbf{\Sigma }}^{(m^{\prime })}]\right)\\ =\text{rank}\left({\mathbf{U}}^{(m)}{\mathbf{\Sigma }}^{(m)}\right)+\text{rank}\left({\mathbf{U}}^{(m^{\prime })}{\mathbf{\Sigma }}^{(m^{\prime })}\right)-\text{rank}\left({\left({\mathbf{U}}^{(m)}{\mathbf{\Sigma }}^{(m)}\right)}^{\mathrm{\top }}\left({\mathbf{U}}^{(m^{\prime })}{\mathbf{\Sigma }}^{(m^{\prime })}\right)\right)\\ =\text{rank}\left({\mathbf{E}}^{(m)}\right)+\text{rank}\left({\mathbf{E}}^{(m^{\prime })}\right)-\text{rank}\left({\left({\mathbf{U}}^{(m)}\right)}^{\mathrm{\top }}{\mathbf{U}}^{(m^{\prime })}\right)\end{array}$$

   其中倒数第二行由 $\mathbf{U}$$\mathbf U$的正交性推导得出。注意：

   $$\text{rank}\left({\left({\mathbf{U}}^{(m)}\right)}^{\mathrm{\top }}{\mathbf{U}}^{(m^{\prime })}\right)={\Vert \cos \left({\varphi }^{m\leftrightarrow m^{\prime }}\right)\Vert }_0$$

   因此，我们将其推广为 $\frac{1}{K}{\Vert \cos ({\varphi }^{m\leftrightarrow m^{\prime }})\Vert }_1$$\frac{1}{K} \left\| \cos(\phi^{m \leftrightarrow m'}) \right\|_{1}$ 来衡量相似性，并使用 1 − similarity 作为多样性。

2. 考虑以下的 example of diversity：一个 embedding size = 2 的 embedding 被学习为：

   $$\begin{array}{c}\mathbf{E}=\left[\begin{array}{cc}1& 0\\ 1& 0\\ 0& 1\\ 0& 1\end{array}\right]\end{array}$$

   其中：$\text{rank}(\mathbf{E})=\text{IA}(\mathbf{E})=2$$\text{rank}(\mathbf E) = \text{IA}(\mathbf E) = 2$ 。

   如果将其扩大到 embedding size = 4，由于 interaction-collapse theory，它可能被学习为：

   $$\begin{array}{c}{\mathbf{E}}^{(1)}=\left[\begin{array}{cc}1& 0\\ 1& 0\\ 0& 1\\ 0& 1\end{array}\right],{\mathbf{E}}^{(2)}=\left[\begin{array}{cc}1& 0\\ 1& 0\\ 0& 1\\ 0& 1\end{array}\right],{\mathbf{E}}^{\text{single}}=\left[\begin{array}{cccc}1& 0& 1& 0\\ 1& 0& 1& 0\\ 0& 1& 0& 1\\ 0& 1& 0& 1\end{array}\right]\end{array}$$

   其中：$\cos \left({\varphi }^{1\leftrightarrow 2}\right)=(1,1)$$\cos\left(\phi^{1\leftrightarrow 2}\right) = (1,1)$，$\text{rank}\left({\mathbf{E}}^{\text{single}}\right)=\text{IA}\left({\mathbf{E}}^{\text{single}}\right)=2$$\text{rank}\left(\mathbf E^\text{single} \right) = \text{IA}\left(\mathbf E^\text{single} \right) = 2$ 。即扩大 embedding size 并没有增加信息丰度。

   当使用 multi-embedding 时，embedding sets 可能被学习为具有高度多样性，overall embedding 被学习为：

   $$\begin{array}{c}{\mathbf{E}}^{(1)}=\left[\begin{array}{cc}1& 0\\ 1& 0\\ 0& 1\\ 0& 1\end{array}\right],{\mathbf{E}}^{(2)}=\left[\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\\ 0& 1\end{array}\right],{\mathbf{E}}^{\text{multi}}=\left[\begin{array}{cccc}1& 0& 1& 0\\ 1& 0& 0& 1\\ 0& 1& 1& 0\\ 0& 1& 0& 1\end{array}\right]\end{array}$$

   其中：$\cos \left({\varphi }^{1\leftrightarrow 2}\right)=(1,0)$$\cos\left(\phi^{1\leftrightarrow 2}\right) = (1,0)$，$\text{rank}\left({\mathbf{E}}^{\text{multi}}\right)=3,\text{IA}\left({\mathbf{E}}^{\text{multi}}\right)=1+\sqrt{2}$$\text{rank}\left(\mathbf E^\text{multi} \right) = 3, \text{IA}\left(\mathbf E^\text{multi} \right) = 1+\sqrt 2$ 。这表明 multi-embedding 是有效的。

2.7 Toy Expermient 的细节 (Appendix G)

1. 在本节中，我们介绍 toy experiment 的详细设置。我们考虑 $N=3$$N=3$ 个 fields 的场景，$D_1=D_2=100$$D_{1}=D_{2}=100$。对于每个 $(x_1,x_2)\in {\mathcal{X}}_1\times {\mathcal{X}}_2$$(x_{1}, x_{2}) \in \mathcal X_{1} \times \mathcal X_{2}$，我们随机分配 $x_3\sim \mathcal{U}[{\mathcal{X}}_3]$$x_{3} \sim \mathcal U[\mathcal X_{3}]$、$y\sim \mathcal{U}\{0,1\}$$y \sim \mathcal U\{0, 1\}$，并将 $(\overrightarrow{\mathbf{x}},y)$$(\mathbf{\vec x}, y)$ 作为一条数据，其中 $\overrightarrow{\mathbf{x}}=(x_1,x_2,x_3)$$\mathbf{\vec x} = (x_1,x_2,x_3)$。因此，对于不同的 $D_3$$D_{3}$ 值，始终有 ${100}^2$$100^2$ 条数据；并且当在 ${\mathcal{X}}_1\times {\mathcal{X}}_2$$\mathcal X_{1} \times \mathcal X_{2}$ 上缩减 $D_3$$D_3$ 时，这 ${100}^2$$100^2$ 条数据遵循相同的分布。我们设置 $D_3=3$$D_{3}=3$ 和 $D_3=100$$D_{3}=100$，分别模拟低信息丰度和高信息丰度的情况。我们使用正态分布 $\mathcal{N}(0,1)$$\mathcal N(0, 1)$ 随机初始化所有 embedding 矩阵，固定 ${\mathbf{E}}_2$$\mathbf E_{2}$、${\mathbf{E}}_3$$\mathbf E_3$，并在训练过程中仅优化 ${\mathbf{E}}_1$$\mathbf E_{1}$。我们使用 full-batch SGD，学习率为 1。模型总共训练 5000 iterations。

2.8 Evidence I 中 FFM 的实证分析 (Appendix H)

1. Field-aware factorization machines: FFM 将 field $i$$i$ 的 embedding 矩阵拆分为多个 sub-embeddings：

   $${\mathbf{E}}_i=[{\mathbf{E}}_i^{\to 1},{\mathbf{E}}_i^{\to 2},\cdots ,{\mathbf{E}}_i^{\to (i-1)},{\mathbf{E}}_i^{\to (i+1)},\cdots ,{\mathbf{E}}_i^{\to N}]$$

   其中： sub-embedding ${\mathbf{E}}_i^{\to j}\in {\mathbb{R}}^{D_i\times K/(N-1)}$$\mathbf E_{i}^{\to j} \in \mathbb{R}^{D_{i} \times K/(N-1)}$ 仅在 field $i$$i$ 与 field $j$$j$（$j\ne i$$j \ne i$）交互时使用。

   我们进行了与 Evidence I 相同的实验，类似地发现 $\text{IA}\left({\mathbf{E}}_i^{\to j}\right)$$\text{IA}\left(\mathbf E_{i}^{\to j}\right)$ 同时受到 $\text{IA}({\mathbf{E}}_i)$$\text{IA}(\mathbf E_{i})$ 和 $\text{IA}({\mathbf{E}}_j)$$\text{IA}(\mathbf E_{j})$ 的共同影响，结果如 Figure 14 所示。这一结果令人惊讶：即使使用独立的 embeddings 来表示相同的 field features，这些 embeddings 在学习后也会具有不同的信息丰度。

   这些 embeddings 在学习之后：即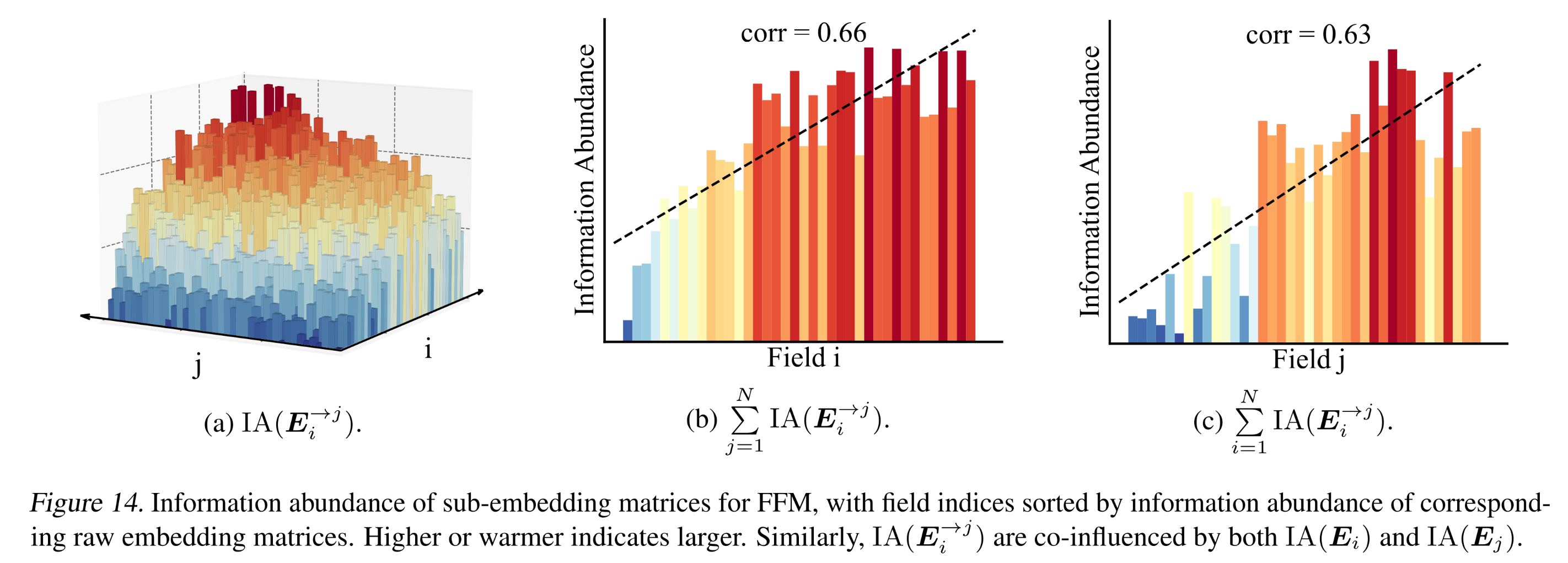 ${\mathbf{E}}_i^{\to j}$$\mathbf E_i^{\to j}$ 。

   

2.9 Information Abundance 的扩展 (Appendix I)

1. 当两个 embedding 矩阵具有相同的 embedding size 时，我们提出的信息丰度是一个公平的度量指标。为了将该定义应用于不同 embedding size 之间的比较，一些可能的扩展包括 $\frac{\text{IA}(\mathbf{E})}{K}$$\frac{\text{IA}(\mathbf E)}{K}$ 和 $\frac{\text{IA}(\mathbf{E})}{\mathbb{E}[\text{IA}(\text{randn.like}(\mathbf{E}))]}$$\frac{\text{IA}(\mathbf E)}{\mathbb{E}[\text{IA}(\text{randn.like}(\mathbf E))]}$，其中：$K$$K$ 表示 embedding size，$\text{randn.like}(\mathbf{E})$$\text{randn.like}(\mathbf E)$ 指与 $\mathbf{E}$$\mathbf E$ 形状相同的正态分布的随机矩阵。

   我们在 Figure 15 中对比了第一种扩展（即， $\frac{\text{IA}(\mathbf{E})}{K}$$\frac{\text{IA}(\mathbf E)}{K}$ ）在不同 embedding size 下的表现。结果表明，collapse 程度随着 embedding size 的增加而加剧：这与 Figure 1b 中的观察结果一致。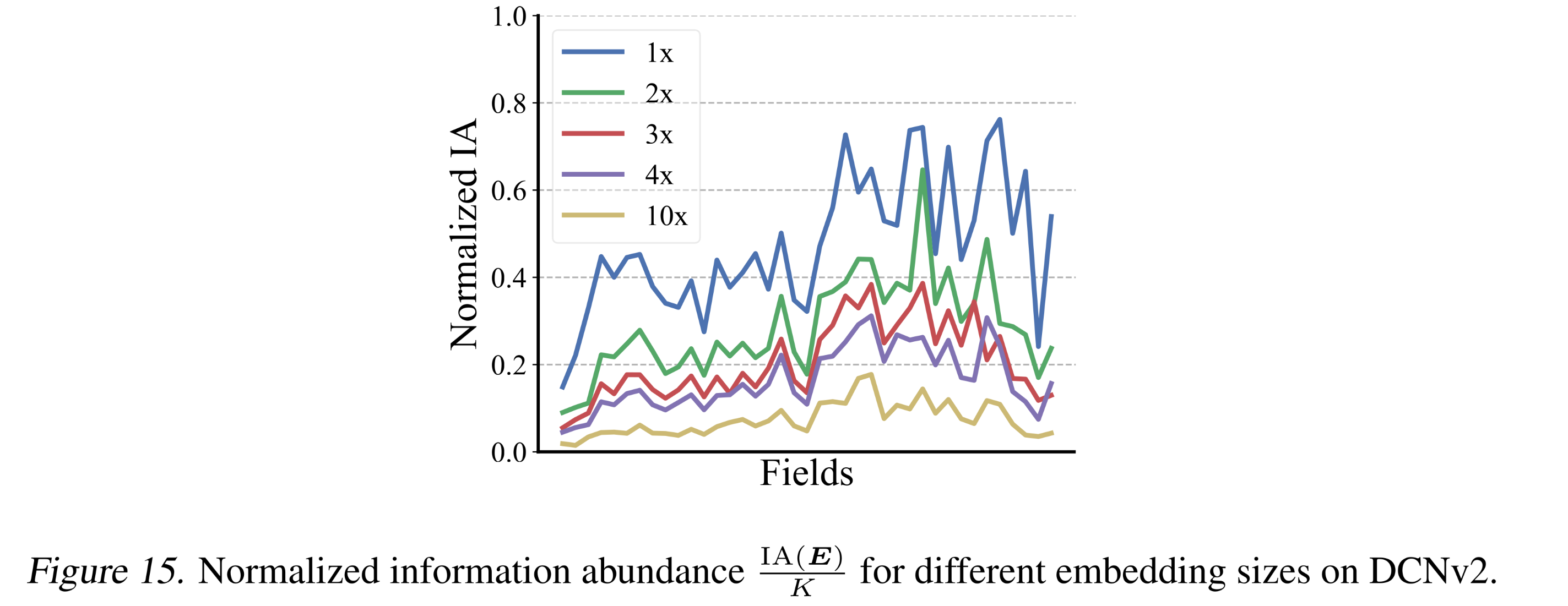

   

2.10 Regularized DCNv2 的详细解释 (Appendix J)

1. 关于 Evidence II，我们提出了对权重矩阵 ${\mathbf{W}}_i^{\to j}$$\mathbf W_{i}^{\to j}$ 的正则化，以缓解 sub-embeddings 中投影 ${\mathbf{W}}_i^{\to j}$$\mathbf W_{i}^{\to j}$ 导致的 collapse。通过将 ${\mathbf{W}}_i^{\to j}$$\mathbf W_{i}^{\to j}$ 正则化为酉矩阵（或酉矩阵的乘积），我们确保 sub-embedding 的所有奇异值都得到保留。因此，regularized DCNv2 中 sub-embeddings 的信息丰度大于 standard DCNv2。我们在 Figure 16 中绘制了 embeddings 和 sub-embeddings 的信息丰度的热力图。这清楚地表明，regularized DCNv2 具有更高的信息丰度。基于我们的 Finding 1，regularized DCNv2 通过增加了 sub-embeddings （这个 sub-embedding 是当前 sub-embedding 直接 interact with 的）的信息丰度，缓解了 embedding collapse 问题。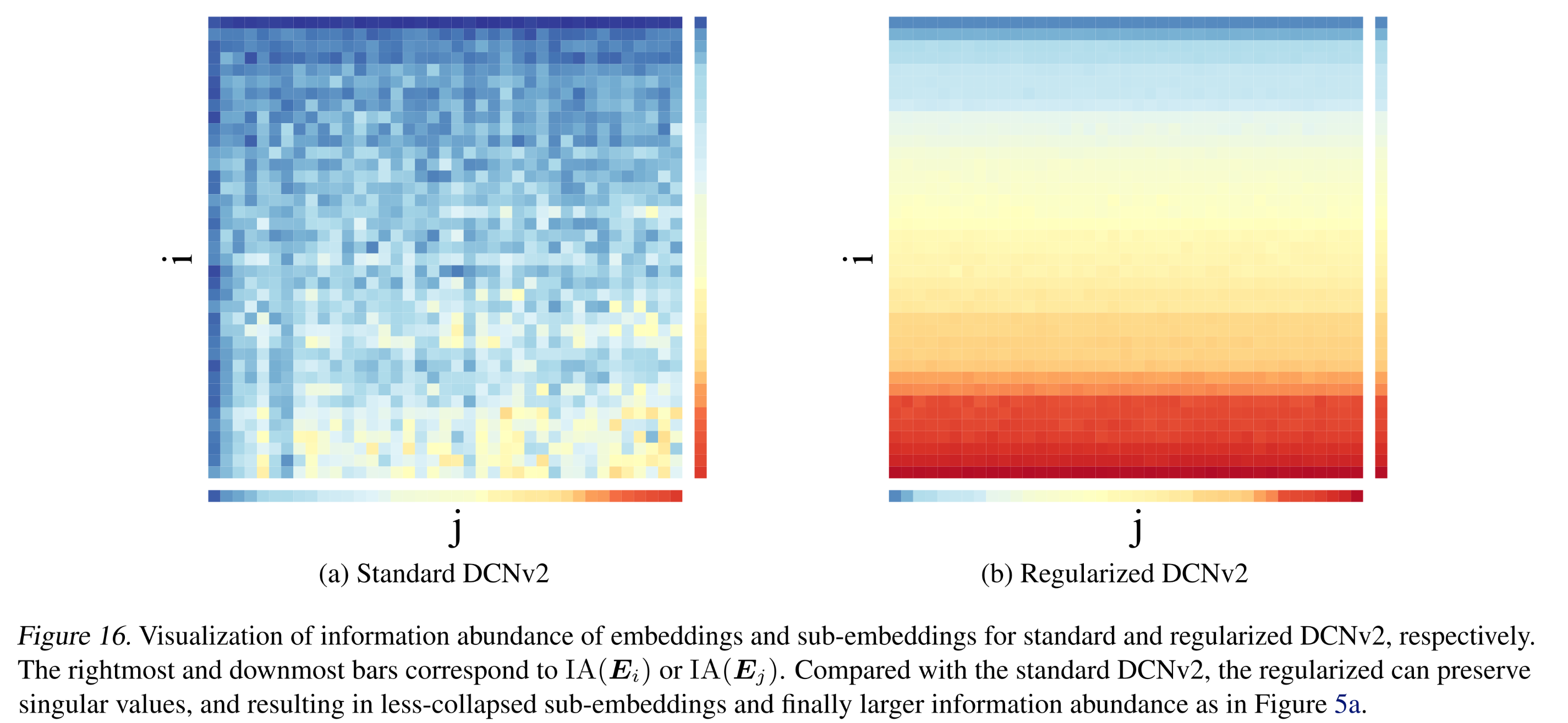

   

2.11 当 Feature Interaction 被抑制时，Multi-Embeddings 的表现如何？(Appendix K)

1. 在本节中，我们分析了 feature interaction 被抑制的模型中的 Multi-Embeddings ——如 1.4.2 节所讨论的，Single-Embeddings 在这些模型中会遭受过拟合。

2. Evidence III for Multi-Embeddings：我们为 Multi-Embedding DCNv2 添加了正则化：

   $${\ell }_{\text{reg}}=\sum _{m=1}^M\sum _{i=1}^N\sum _{j=1}^N{\Vert {\left({\mathbf{W}}_{i\to j}^{(m)}\right)}^{\mathrm{\top }}{\mathbf{W}}_{i\to j}^{(m)}-{\lambda }_{ij}^{(m)}\mathbf{I}\Vert }_F^2$$

   并在不同 embedding size 下进行了实验。结果如 Figure 17a 所示。尽管其性能低于 without regularization 的情况，但与Single-Embeddings 相比，Multi-Embeddings 仍然随着模型规模的增长持续提升性能。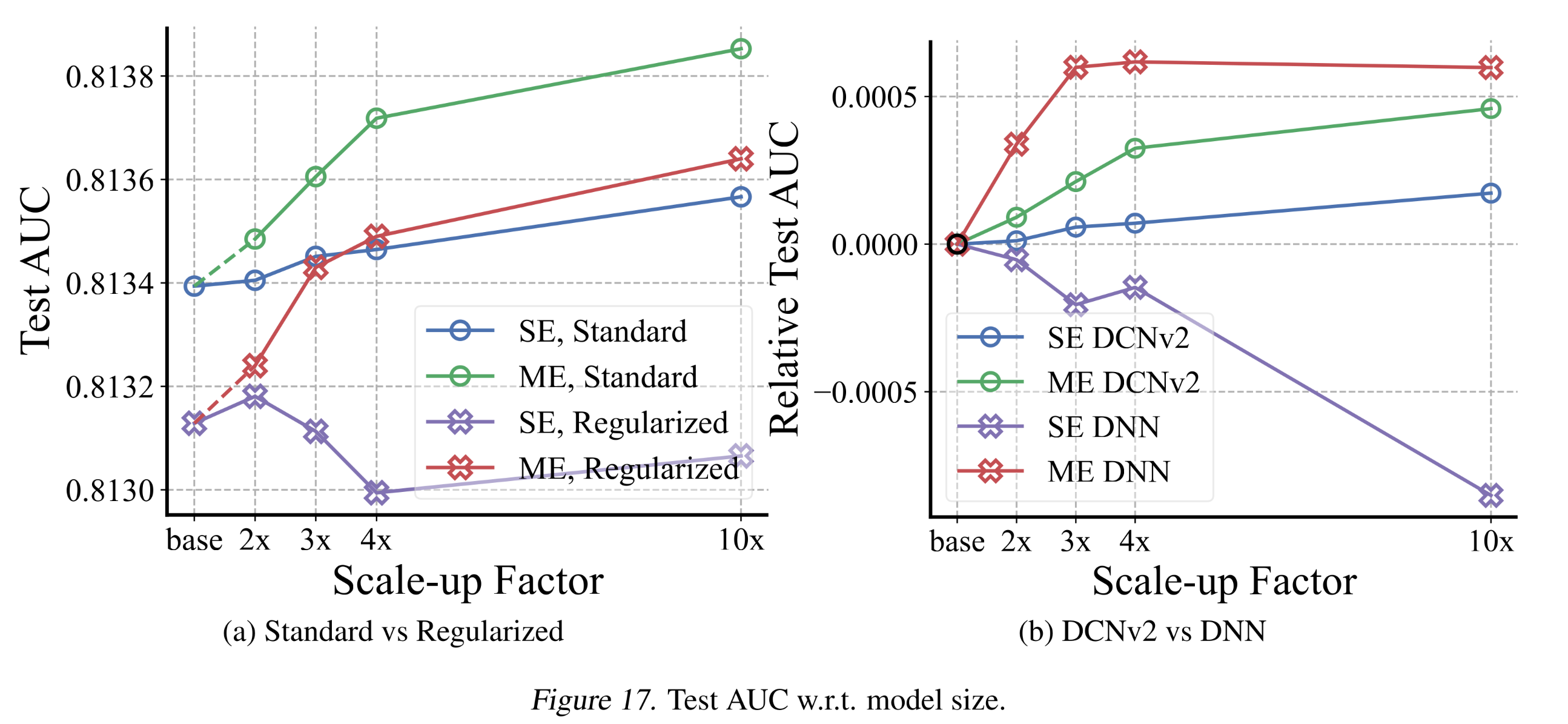

   

3. Evidence IV for Multi-Embeddings：我们对比了 Single-Embeddings/Multi-Embeddings 在 DNN/DCNv2 上的性能，结果如Figure 17b 所示。与 Single-Embeddings DNN 相比，Multi-Embeddings DNN 随着模型规模的增长提升了性能。

4. 总结：即使 feature interaction 被抑制，Multi-Embeddings 仍能提供 scalability。对于 feature interaction 被抑制的模型（如 regularized DCNv2 和 DNN），Single-Embeddings 的性能可能会随着模型规模的扩大而下降——因为 feature interaction 提供了 domain knowledge，而大型模型可能会遭受过拟合。实验表明，这些模型与 Multi-Embeddings 结合后能够实现适当的 scale up。这一结果是合理的，因为 Multi-Embeddings 通过捕获 diverse patterns 来提升 scalability，而不是依赖单个 interaction pattern 进行学习。