一、TiSASRec [2020]

《Time Interval Aware Self-Attention for Sequential Recommendation》

1. 有两个重要的方向旨在挖掘用户的历史交互：时间推荐（temporal recommendation）和序列推荐（sequential recommendation）。

   时间推荐侧重于建模绝对时间戳从而捕获用户和 item 的时间动态（ temporal dynamics）。例如，一个 item 的热门程度可能会在不同的时间段内发生变化，或者一个用户的平均评分可能会随着时间的推移而增加或减少。这些模型在探索数据集中的时间变化（temporal change）时很有用。它们不考虑序列模式（sequential pattern），而是考虑依赖于时间的时间模式（temporal pattern）。

   大多数以前的序列推荐器通过交互时间戳对 item 进行排序，并聚焦于序列模式挖掘来预测 next item 。

   • 一种典型的解决方案是基于马尔科夫链的方法，其中 L 阶马尔科夫链根据 L 个先前的动作而作出推荐。基于马尔科夫链的方法已经成功应用于捕获短期 item transition 从而用于推荐。这些方法通过作出很强的简化假设并在高度稀疏场景下表现良好，但是在更复杂的场景中可能无法捕获到复杂的动态（intricate dynamics）。

   • RNN 也可用于序列推荐。虽然 RNN 模型对用户的偏好有很长的“记忆”，但是模型需要大量数据（尤其是稠密数据）才能超越更简单的 baseline。

   • 为了解决马尔科夫链模型和 RNN-based 模型的缺点，受到 Transformer 的启发，SASRec 提出将自注意力机制应用于序列推荐问题。基于自注意力机制的模型显著优于 SOTA 的 MC/CNN/RNN based 序列推荐方法。

   一般而言，以前的序列推荐器会丢弃时间戳信息并且仅保留 item 的顺序。即，这些方法隐式地假设序列中的所有相邻 item 具有相同的时间间隔。影响后续的 item 的因素仅有前面 item 的 id 和位置。然而，直观而言，具有most recent 时间戳的 item 将对 next item 产生更大的影响。例如，两个用户具有相同的交互序列，其中一个用户在一天之内完成了这些交互而另一个用户在一个月之内完成了这些交互。因此，这两个用户的交互对于 next item 的影响应该是不同的，即使他们具有相同的交互序列。然而，先前的序列推荐技术将这两种情况视为相同，因为它们仅考虑 sequential position（而未考虑 sequential timestamp ）。

   在论文 《Time Interval Aware Self-Attention for Sequential Recommendation》 中，作者认为应该将用户交互序列建模为具有不同时间间隔的序列。下图表明：交互序列具有不同的时间间隔，其中一些时间间隔可能很大。以前的工作忽略了这些时间间隔对被预测的 item 的影响。为了解决上述限制，受到 Self-Attention with Relative Position Representation 的启发，作者提出了一种 time-aware self-attention 机制，即 TiSASRec 模型。该模型不仅像 SASRec 一样考虑了 item 的绝对位置（absolute position），还考虑了任意两个 item 之间的相对时间间隔。从论文的实验中可以观察到，论文提出的模型在稠密数据集和稀疏数据集上都优于 SOTA 算法。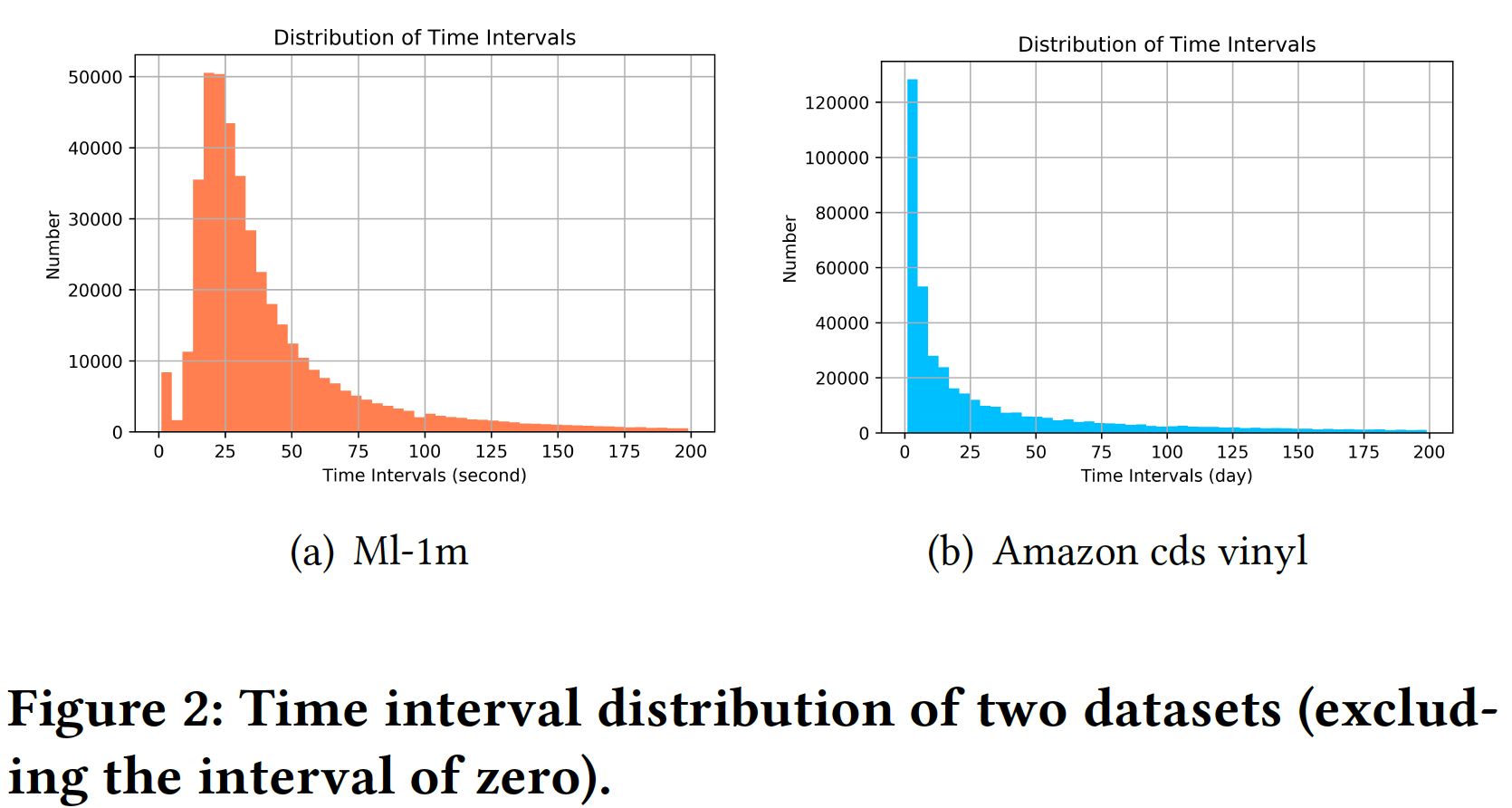

   

   最后，论文的贡献如下：

   • 作者提出将用户的交互历史视为具有不同时间间隔的序列，并将不同时间间隔建模为任意两个交互之间的关系（relation）。

   • 作者将绝对位置编码（absolute position encoding）和相对时间间隔编码（relative time interval encoding）的优势相结合从而用于 self-attention ，并且设计了一种新颖的 time interval aware 的 self-attention 机制来学习不同 item, absolute position, time interval 的权重从而预测 next item 。

   • 作者进行了彻底的实验来研究绝对位置和相对时间间隔以及不同组件对 TiSASRec 性能的影响，并表明 TiSASRec 在两个指标上优于 SOTA 的 baseline 。

2. 相关工作：

   • 序列推荐：序列推荐系统挖掘用户交互序列中的模式。

     • 一些方法捕获 item-item 转移矩阵来预测 next item 。例如：FPMC 通过矩阵分解和转移矩阵（transition matrix）来建模用户的长期偏好和动态转移（dynamic transition）。

       转移矩阵是一阶马尔科夫链，它仅考虑当前item 和前一个 item 之间的关系。Fossil 使用基于相似性的方法和高阶马尔科夫链，假设 next item 和前面几个 item 相关，而 《Translation-based Recommendation》 证明了基于高阶马尔科夫链的模型在稀疏数据集上具有强大的性能。

     • 人们也提出了 CNN-based 方法（如，Caser，《3D Convolutional Networks for Session-based Recommendation with Content Feature》）从而将先前的若干个 item 视为 “图像”，然后通过 union-level 的 CNN 来挖掘 item 之间的转移。

     • MARank 通过结合残差网络和多阶注意力来统一 individual-level 和 union-level 的 previous item transitions 。

     • SHAN 通过两层注意力机制来建模用户的 previous several items 和长期历史，从而获得用户的短期偏好和长期偏好。

     • RNN-based 模型（如，《Latent Cross: Making Use of Context in Recurrent Recommender Systems》、GRU4Rec、《Neural Survival Recommender》、《Context-Aware Sequential Recommendation》） 使用RNN 来建模整个用户序列。这些方法在稠密数据集上表现良好，但是在稀疏数据集上通常表现不佳。

   • 注意力机制：注意力机制已被证明在 image captioning 和机器翻译等任务上是有效的。本质上，注意力机制背后的思想是：output 依赖于 input 中相关的特定部分。这种机制可以计算 input 的权重并使得模型更易于解释。最近，人们将注意力机制纳入推荐系统（《Attentive Collaborative Filtering: Multimedia Recommendation with Item- and Component-Level Attention》、《Attention-Based Transactional Context Embedding for Next-Item Recommendation》、《Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks》）。

     Transformer 是一种纯粹基于注意力的 sequence-to-sequence 方法，并且在机器翻译任务上取得了 SOTA 性能。Transformer 使用缩放的内积注意力，其定义为：

     $$\text{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\text{softmax}\left(\frac{\mathbf{Q}{\mathbf{K}}^{\mathrm{\top }}}{\sqrt{d}}\right)\mathbf{V}$$

     其中：$\mathbf{Q},\mathbf{K},\mathbf{V}$$\mathbf Q,\mathbf K,\mathbf V$ 分别代表 query, key, value 。在 self-attention 中，这三个输入通常使用相同的object 。

     Transformer 的自注意力模块也被用于推荐系统（如，SASRec），并在序列推荐上取得了 SOTA 的结果。由于自注意力模型不包含任何循环模块或卷积模块，因此它不知道前面所有 item 的位置。

     • 一种解决方案是向 input 添加 positional encoding ，其中 positional encoding 可以是确定性函数或者可学习的参数。

     • 另一种解决方案是使用 relative position representation 。该方法将两个 input 之间的相对位置建模为 pairwise relationship 。

     受到带有相对位置的 self-attention 的启发，我们结合 absolute position 和 relative position 来设计 time-aware self-attention 从而建模 item 的位置和时间间隔。

     目前已有一些工作探索了时间间隔对序列推荐的影响，如 Time-LSTM 。但是作者这里尚未提及。

1.1 模型

1. 我们的 TiSASRec 包含个性化的时间间隔处理（personalized time interval processing）、一个 emebdding layer、几个 time-aware self-attention块 、以及一个 prediction layer 。我们嵌入 item 、item 的绝对位置、以及 item 之间的相对时间间隔。我们通过这些 emebdding 来计算注意力权重。如下图所示，即使先前的几个 item 相同，我们的模型也会在不同的时间间隔下提供不同的 predicted item 。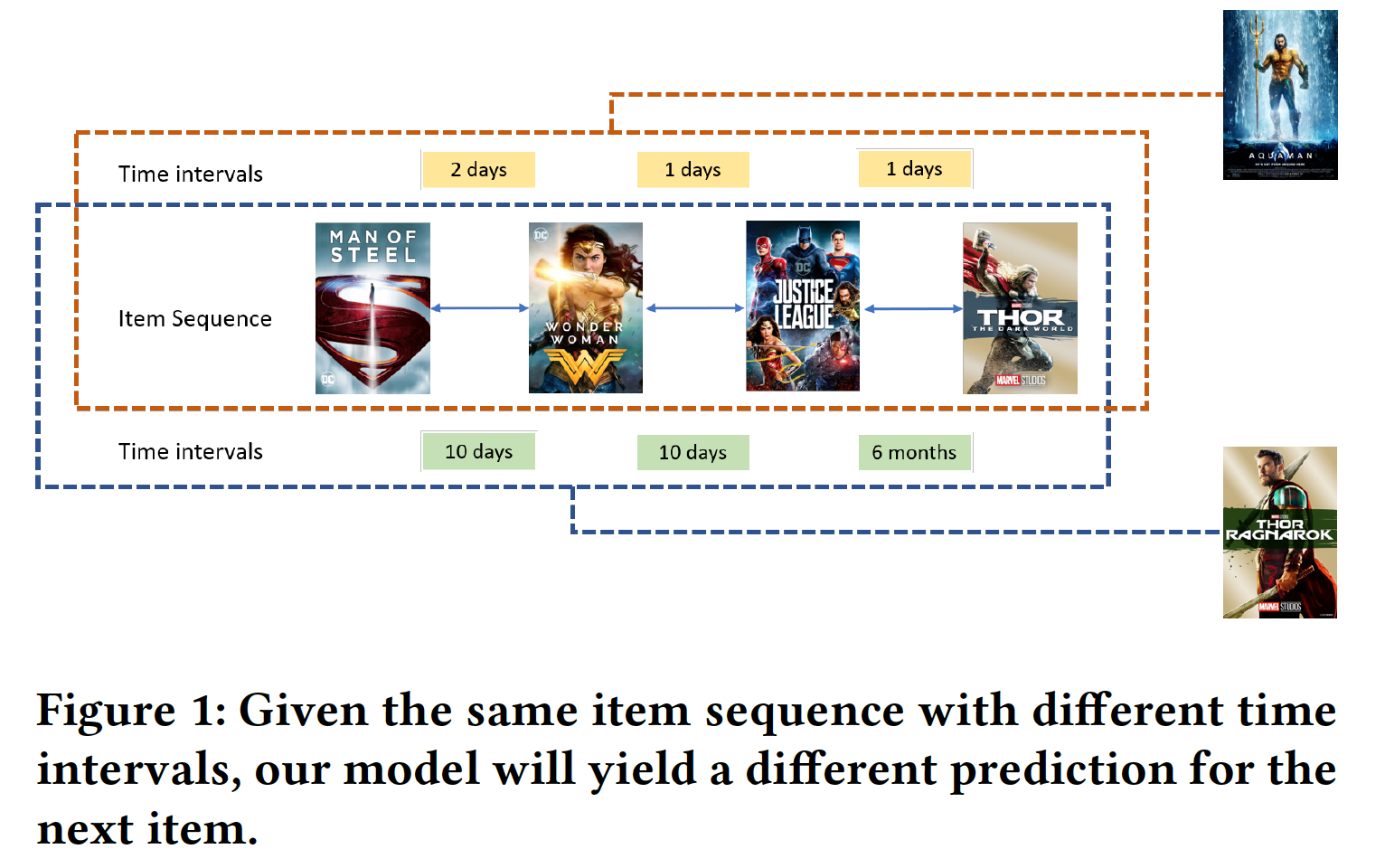

   

   为了学习模型参数，我们采用二元交叉熵作为损失函数。TiSASRec 的目标是捕获序列模式并探索时间间隔对序列推荐的影响，而这是一个尚未探索的领域。

   TiSASRec 的模型结构如下图所示。

   论文的核心就是在 SASRec 上增加了相对时间间隔 embedding 。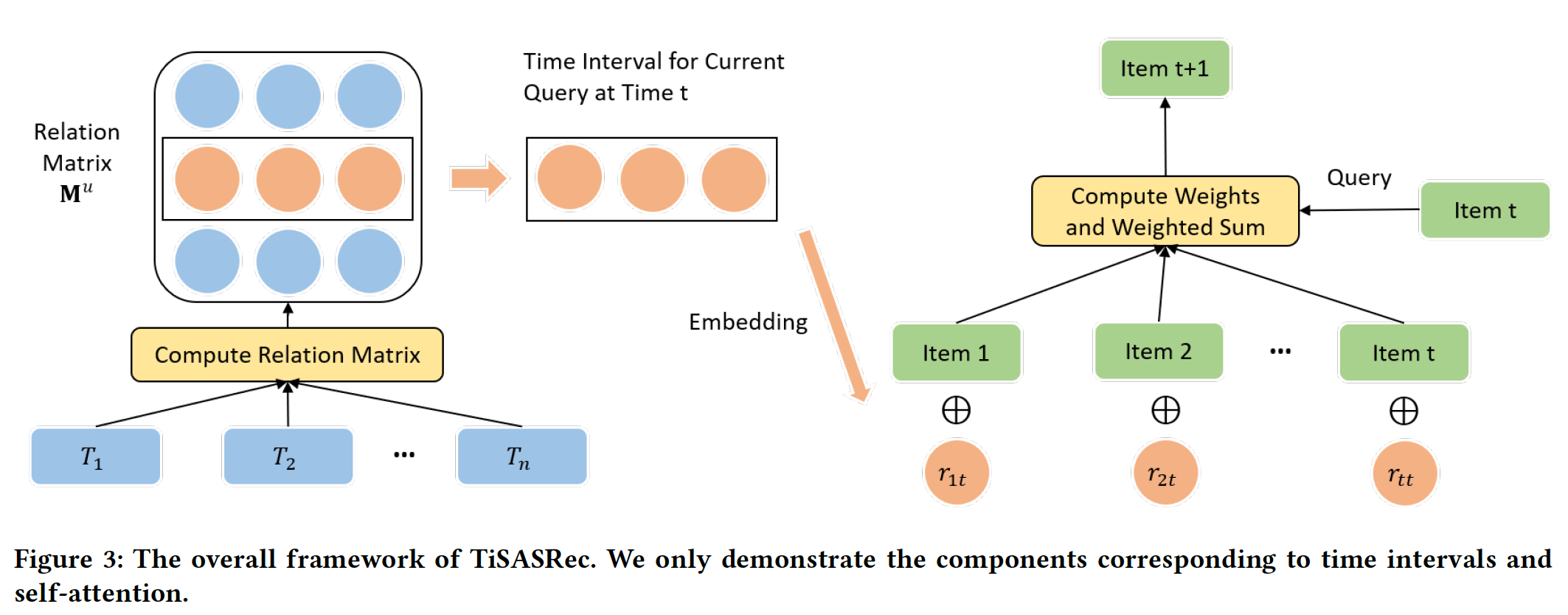

   

2. 令 $\mathcal{U}$$\mathcal U$ 为用户集合，$\mathcal{I}$$\mathcal I$ 为 item 集合。在 time-aware 序列推荐的 setting 中，对于每个用户 $u\in \mathcal{U}$$u\in \mathcal U$ ，我们已知用户 $u$$u$ 根据时间戳排序的 action 序列 ${\mathcal{S}}^{(u)}=(S_1^{(u)},S_2^{(u)},\cdots ,S_{|{\mathcal{S}}^{(u)}|}^{(u)})$$\mathcal S^{(u)} = \left(S_1^{(u)},S_2^{(u)},\cdots,S_{|\mathcal S^{(u)}|}^{(u)}\right)$ ，其中 $S_i^{(u)}\in \mathcal{I}$$S_i^{(u)}\in \mathcal I$ 。此外，我们还知道 ${\mathcal{S}}^{(u)}$$\mathcal S^{(u)}$ 中每个 action 发生时间的时间序列 ${\mathcal{T}}^{(u)}=(T_1^{(u)},T_2^{(u)},\cdots ,T_{|{\mathcal{S}}^{(u)}|}^{(u)})$$\mathcal T^{(u)}=\left(T_1^{(u)},T_2^{(u)},\cdots,T_{|\mathcal S^{(u)}|}^{(u)}\right)$ 。在训练过程中，在 time step $t$$t$ ，模型根据先前的 $t$$t$ 个 item 以及 item $i$$i$ 和 $j$$j$ 之间的时间间隔 $r_{i,j}^{(u)}$$r_{i,j}^{(u)}$ 来预测 next item 。

   我们模型的输入是 $(S_1^{(u)},S_2^{(u)},\cdots ,S_{|{\mathcal{S}}^{(u)}|-1}^{(u)})$$\left(S_1^{(u)},S_2^{(u)},\cdots,S_{|\mathcal S^{(u)}|-1}^{(u)}\right)$ 以及任意两个 item 之间的时间间隔矩阵 ${\mathbf{R}}^{(u)}$$\mathbf R^{(u)}$ ，我们期望的输出是每个 time step 的 next item ： $(S_2^{(u)},S_3^{(u)},\cdots ,S_{|{\mathcal{S}}^{(u)}|}^{(u)})$$\left(S_2^{(u)},S_3^{(u)},\cdots,S_{|\mathcal S^{(u)}|}^{(u)}\right)$。

   ${\mathbf{R}}^{(u)}\in {\mathbb{R}}^{(|{\mathcal{S}}^{(u)}|-1)\times (|{\mathcal{S}}^{(u)}|-1)}$$\mathbf R^{(u)}\in \mathbb R^{\left(|\mathcal S^{(u)}|-1\right)\times \left(|\mathcal S^{(u)}|-1\right)}$ 由 ${\left\{r_{i,j}^{(u)}\right\}}_{1\le i,j\le |{\mathcal{S}}^{(u)}|-1}$$\left\{r_{i,j}^{(u)}\right\}_{1\le i,j\le |\mathcal S^{(u)}|-1}$组成。注意，这里并未考虑 time step $|{\mathcal{S}}^{(u)}|$$|\mathcal S^{(u)}|$ 从而防止信息泄露，因为这是 next item 的信息。

   事实上也可以考虑 time step $|{\mathcal{S}}^{(u)}|$$|\mathcal S^{(u)}|$ ，在预测期间它就是 current timestamp 作为时间上下文。

1.1.1 个性化时间间隔

1. 我们将训练序列 $(S_1^{(u)},S_2^{(u)},\cdots ,S_{|{\mathcal{S}}^{(u)}|-1}^{(u)})$$\left(S_1^{(u)},S_2^{(u)},\cdots,S_{|\mathcal S^{(u)}|-1}^{(u)}\right)$ 转换为固定长度的序列 $\mathbf{s}=(s_1,s_2,\cdots ,s_n)$$\mathbf s = (s_1,s_2,\cdots,s_n)$ ，其中 $n$$n$ 为我们考虑的最大长度。

   • 如果训练序列长度 $|{\mathcal{S}}^{(u)}|-1$$|\mathcal S^{(u)}|-1$ 大于 $n$$n$ ，则我们仅考虑最近的 $n$$n$ 个 item 。

   • 如果训练序列长度 $|{\mathcal{S}}^{(u)}|-1$$|\mathcal S^{(u)}|-1$ 小于 $n$$n$ ，则我们在序列左侧添加 padding item 直到长度为 $n$$n$ 。

   类似地，我们对于时间序列 $(T_1^{(u)},T_2^{(u)},\cdots ,T_{|{\mathcal{S}}^{(u)}|-1}^{(u)})$$\left(T_1^{(u)},T_2^{(u)},\cdots,T_{|\mathcal S^{(u)}|-1}^{(u)}\right)$ 也考虑固定长度的时间序列 $\mathbf{t}=(t_1,t_2,\cdots ,t_n)$$\mathbf t = (t_1,t_2,\cdots,t_n)$ 。如果时间序列长度小于 $n$$n$ ，则我们在序列左侧填充第一个时间戳 $T_1^{(u)}$$T_1^{(u)}$ ；否则我们仅考虑最近的 $n$$n$ 个时间戳。

2. 我们将交互序列中的时间间隔建模为两个 item 之间的关系。一些用户有更频繁的交互，而另一些用户则没那么频繁，我们仅关心用户序列中时间间隔的相对长度。因此，对于所有时间间隔，我们除以用户序列中最短的时间间隔（0 除外）来获得个性化的时间间隔。

   具体而言，给定用户 $u$$u$ 的固定长度时间序列 $\mathbf{t}=(t_1,t_2,\cdots ,t_n)$$\mathbf t=(t_1,t_2,\cdots,t_n)$ ，两个 item $i$$i$ 和 $j$$j$ 之间的时间间隔为 $|t_i-t_j|$$|t_i - t_j|$ 。我们将用户的最小时间间隔定义为：

   $$r_{min}^{(u)}=\underset{1\le i,j\le n,i\ne j}{min}(|t_i-t_j|)$$

   缩放后的时间间隔 ${\tilde{r}}_{i,j}^{(u)}\in \mathbb{N}$$\tilde r_{i,j}^{(u)}\in \mathbb N$ 为：

   $${\tilde{r}}_{i,j}^{(u)}=\lfloor \frac{|t_i-t_j|}{r_{min}^{(u)}}\rfloor$$

   其中 $\lfloor \cdot \rfloor$$\lfloor\cdot\rfloor$ 为向下取整函数。

   根据定义有： ${\tilde{r}}_{i,j}^{(u)}\ge 1$$\tilde r_{i,j}^{(u)} \ge 1$ 。

   因此，用户 $u$$u$ 的关系矩阵（relation matrix）${\mathbf{M}}^{(u)}\in {\mathbb{R}}^{n\times n}$$\mathbf M^{(u)}\in \mathbb R^{n\times n}$ 定义为：

   $$\begin{array}{c}{\mathbf{M}}^{(u)}=\left[\begin{array}{cccc}{\tilde{r}}_{1,1}^{(u)}& {\tilde{r}}_{1,2}^{(u)}& \cdots & {\tilde{r}}_{1,n}^{(u)}\\ {\tilde{r}}_{2,1}^{(u)}& {\tilde{r}}_{2,2}^{(u)}& \cdots & {\tilde{r}}_{2,n}^{(u)}\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{r}}_{n,1}^{(u)}& {\tilde{r}}_{n,2}^{(u)}& \cdots & {\tilde{r}}_{n,n}^{(u)}\end{array}\right]\end{array}$$

   为什么用个性化的时间间隔，而不使用绝对的时间间隔，例如 ${\tilde{r}}_{i,j}^{(u)}=\lfloor \frac{|t_i-t_j|}{\text{1 hour}}\rfloor$$\tilde r_{i,j}^{(u)} = \left \lfloor\frac{|t_i - t_j|}{\text{1 hour}}\right\rfloor$ ？作者这里并未给出原因。可以做实验验证绝对时间间隔的效果。

3. 我们考虑的两个 item 之间的最大相对时间间隔被截断为 $k$$k$ 。我们假设：相对时间间隔超过了某个阈值之后是没有价值的。截断最大相对时间间隔还避免了稀疏关系编码（sparse relation encoding）（即，裁剪后的关系矩阵大多数元素为零），并且使得模型能够泛化到训练期间 unseen 的时间间隔。因此，裁剪后的矩阵为：

   $${\mathbf{M}}_{\text{clipped}}^{(u)}=\text{clip}\left({\mathbf{M}}^{(u)}\right)$$

   其中：矩阵的 $\text{clip}(\cdot )$$\text{clip}(\cdot)$ 操作应用到矩阵的每个元素，即，${\tilde{r}}_{i,j}^{(u)}\leftarrow min(k,{\tilde{r}}_{i,j}^{(u)})$$\tilde r_{i,j}^{(u)} \leftarrow \min\left(k,\tilde r_{i,j}^{(u)}\right)$。

1.1.2 Embedding Layer

1. 我们为所有 item 创建一个 item embedding ${\mathbf{M}}_I\in {\mathbb{R}}^{|\mathcal{I}|\times d}$$\mathbf M_I \in \mathbb R^{|\mathcal I|\times d}$ ，其中 $d$$d$ 为 embedding 维度。对于 padding item，它的 embedding 固定为零向量。

   给定固定长度的序列 $\mathbf{s}=(s_1,s_2,\cdots ,s_n)$$\mathbf s = (s_1,s_2,\cdots,s_n)$ ，embedding look-up 操作查找这 $n$$n$ 个item 的 embedding，将它们堆叠在一起从而得到一个矩阵 ${\mathbf{E}}_I\in {\mathbb{R}}^{n\times d}$$\mathbf E_I \in \mathbb R^{n\times d}$ ：

   $$\begin{array}{c}{\mathbf{E}}^{(I)}=\left[\begin{array}{c}{\overrightarrow{\mathbf{m}}}_{s_1}\\ {\overrightarrow{\mathbf{m}}}_{s_2}\\ ⋮\\ {\overrightarrow{\mathbf{m}}}_{s_n}\end{array}\right]\end{array}$$

   其中 ${\overrightarrow{\mathbf{m}}}_i$$\mathbf{\vec m}_i$ 为 ${\mathbf{M}}_I$$\mathbf M_I$ 的第 $i$$i$ 行，代表 item $i\in \mathcal{I}$$i\in \mathcal I$ 的 embedding 向量。

2. 遵从 《Self-Attention with Relative Position Representations》 ，我们使用两个不同的可学习的 positional embedding matrix ，即 ${\mathbf{M}}_{P,K}\in {\mathbb{R}}^{n\times d}$$\mathbf M_{P,K}\in \mathbb R^{n\times d}$ 和 ${\mathbf{M}}_{P,V}\in {\mathbb{R}}^{n\times d}$$\mathbf M_{P,V}\in \mathbb R^{n\times d}$ ，它们分别用于 self-attention 机制中的 key 和 value 。

   给定固定长度的序列 $\mathbf{s}=(s_1,s_2,\cdots ,s_n)$$\mathbf s = (s_1,s_2,\cdots,s_n)$ ，我们根据这 $n$$n$ 个 item 的位置检索得到 emebdding 矩阵 ${\mathbf{E}}_{P,K}\in {\mathbb{R}}^{n\times d}$$\mathbf E_{P,K}\in \mathbb R^{n\times d}$ 和 ${\mathbf{E}}_{P,V}\in {\mathbb{R}}^{n\times d}$$\mathbf E_{P,V}\in \mathbb R^{n\times d}$ ，即：

   $$\begin{array}{c}{\mathbf{E}}_{P,K}=\left[\begin{array}{c}{\overrightarrow{\mathbf{p}}}_{K,1}\\ {\overrightarrow{\mathbf{p}}}_{K,2}\\ ⋮\\ {\overrightarrow{\mathbf{p}}}_{K,n}\end{array}\right],{\mathbf{E}}_{P,V}=\left[\begin{array}{c}{\overrightarrow{\mathbf{p}}}_{V,1}\\ {\overrightarrow{\mathbf{p}}}_{V,2}\\ ⋮\\ {\overrightarrow{\mathbf{p}}}_{V,n}\end{array}\right]\end{array}$$

   其中：

   • ${\overrightarrow{\mathbf{p}}}_{K,i}$$\mathbf{\vec p}_{K,i}$ 为 ${\mathbf{M}}_{P,K}$$\mathbf M_{P,K}$ 的第 $i$$i$ 行，代表 position $i$$i$ 用于 key 的 positional embedding 。

   • ${\overrightarrow{\mathbf{p}}}_{V,i}$$\mathbf{\vec p}_{V,i}$ 为 ${\mathbf{M}}_{P,V}$$\mathbf M_{P,V}$ 的第 $i$$i$ 行，代表 position $i$$i$ 用于 value 的 positional embedding 。

   用两组 embedding 来表达 positional embedding 会增强模型的容量从而提高模型的表达能力，但是效果是否更好？这个可以通过实验来比较。

3. 类似于 positional embedding，相对时间间隔 embedding matrix 为 ${\mathbf{M}}_{R,K}\in {\mathbb{R}}^{k\times d}$$\mathbf M_{R,K}\in \mathbb R^{k\times d}$ 和 ${\mathbf{M}}_{R,V}\in {\mathbb{R}}^{k\times d}$$\mathbf M_{R,V}\in \mathbb R^{k\times d}$ ，它们分别用于 self-attention 机制中的 key 和 value 。在检索裁剪后的关系矩阵 ${\mathbf{M}}_{\text{clipped}}^{(u)}$$\mathbf M^{(u)}_\text{clipped}$ 之后，我们得到 embedding 张量 ${\mathbf{E}}_{R,K}\in {\mathbb{R}}^{n\times n\times d}$$\mathbf E_{R,K}\in \mathbb R^{n\times n\times d}$ 和 ${\mathbf{E}}_{R,V}\in {\mathbb{R}}^{n\times n\times d}$$\mathbf E_{R,V}\in \mathbb R^{n\times n\times d}$ ，即：

   $$\begin{array}{c}{\mathbf{E}}_{R,K}=\left[\begin{array}{cccc}{\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{1,1}}& {\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{1,2}}& \cdots & {\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{1,n}}\\ {\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{2,1}}& {\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{2,2}}& \cdots & {\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{2,n}}\\ ⋮& ⋮& \ddots & ⋮\\ {\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{n,1}}& {\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{n,2}}& \cdots & {\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{n,n}}\end{array}\right],{\mathbf{E}}_V^{(R)}=\left[\begin{array}{cccc}{\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{1,1}}& {\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{1,2}}& \cdots & {\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{1,n}}\\ {\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{2,1}}& {\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{2,2}}& \cdots & {\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{2,n}}\\ ⋮& ⋮& \ddots & ⋮\\ {\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{n,1}}& {\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{n,2}}& \cdots & {\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{n,n}}\end{array}\right]\end{array}$$

   其中：

   • ${\overrightarrow{\mathbf{r}}}_{K,i}$$\mathbf{\vec r}_{K,i}$ 为 ${\mathbf{M}}_{R,K}$$\mathbf M_{R,K}$ 的第 $i$$i$ 行，代表相对时间间隔 $i$$i$ 用于 key 的 embedding 。

   • ${\overrightarrow{\mathbf{r}}}_{V,i}$$\mathbf{\vec r}_{V,i}$ 为 ${\mathbf{M}}_{R,V}$$\mathbf M_{R,V}$ 的第 $i$$i$ 行，代表相对时间间隔 $i$$i$ 用于 value 的embedding 。

   这两个相对时间间隔 embedding 矩阵是对称矩阵（其实是张量），并且主对角线上的元素全为零。

   类似地，这里用两组 embedding 来表达相对时间间隔 embedding 会增强模型的容量从而提高模型的表达能力，但是效果是否更好？这个可以通过实验来比较。

1.1.3 Time Interval-Aware 自注意力

1. 受相对位置自注意力机制的启发，我们提出了对自注意力的扩展从而考虑序列中两个 item 之间的不同时间间隔。但是，仅考虑时间间隔是不够的，因为用户交互序列可能有许多具有相同时间戳的item 。在这种情况下，模型将成为没有任何位置信息或关系信息的 self-attention 。因此，我们还考虑了 item 在序列中的位置。

   例如，假设时间间隔都是相等的，那么 ${\tilde{r}}_{i,j}^{(u)}=\lfloor \frac{|t_i-t_j|}{r_{min}^{(u)}}\rfloor$$\tilde r_{i,j}^{(u)} = \left \lfloor\frac{|t_i - t_j|}{r_\min^{(u)} }\right\rfloor$ 恒等于 1，因此会丢失位置信息。

2. Time Interval-Aware Self-attention Layer：对于每个长度为 $n$$n$ 的输入序列 $({\overrightarrow{\mathbf{m}}}_{s_1},{\overrightarrow{\mathbf{m}}}_{s_2},\cdots ,{\overrightarrow{\mathbf{m}}}_{s_n})$$\left(\mathbf{\vec m}_{s_1},\mathbf{\vec m}_{s_2},\cdots,\mathbf{\vec m}_{s_n}\right)$ ，其中 ${\overrightarrow{\mathbf{m}}}_{s_i}\in {\mathbb{R}}^d$$\mathbf{\vec m}_{s_i}\in \mathbb R^d$ 为 item $s_i\in \mathcal{I}$$s_i\in \mathcal I$ 的 item embedding ，我们计算一个新的序列 $({\overrightarrow{\mathbf{z}}}_1,{\overrightarrow{\mathbf{z}}}_2,\cdots ,{\overrightarrow{\mathbf{z}}}_n)$$\left(\mathbf{\vec z}_1,\mathbf{\vec z}_2,\cdots,\mathbf{\vec z}_n\right)$，其中 ${\overrightarrow{\mathbf{z}}}_i\in {\mathbb{R}}^d$$\mathbf{\vec z}_i\in \mathbb R^d$ 。每个输出 ${\overrightarrow{\mathbf{z}}}_i$$\mathbf{\vec z}_i$ 被计算为：

   $${\overrightarrow{\mathbf{z}}}_i=\sum _{j=1}^n{\alpha }_{i,j}({\overrightarrow{\mathbf{m}}}_{s_j}{\mathbf{W}}_V+{\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{i,j}}+{\overrightarrow{\mathbf{p}}}_{V,j})$$

   其中：

   • ${\mathbf{W}}_V\in {\mathbb{R}}^{d\times d}$$\mathbf W_V\in \mathbb R^{d\times d}$ 为用于 value 的待学习的投影矩阵。

   • 每个权重系数 ${\alpha }_{i,j}$$\alpha_{i,j}$ 是通过 softmax 函数来计算：

     $${\alpha }_{i,j}=\frac{\exp (e_{i,j})}{\sum _{j^{\prime }=1}^n\exp (e_{i,j^{\prime }})},e_{i,j}=\frac{\left({\overrightarrow{\mathbf{m}}}_{s_i}{\mathbf{W}}_Q\right){({\overrightarrow{\mathbf{m}}}_{s_j}{\mathbf{W}}_K+{\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{i,j}}+{\overrightarrow{\mathbf{p}}}_{K,j})}^{\mathrm{\top }}}{\sqrt{d}}$$

     其中：${\mathbf{W}}_Q\in {\mathbb{R}}^{d\times d}$$\mathbf W_Q\in \mathbb R^{d\times d}$ 和 ${\mathbf{W}}_K\in {\mathbb{R}}^{d\times d}$$\mathbf W_K\in \mathbb R^{d\times d}$ 分别是用于 query 和 key 的待学习的投影矩阵。缩放因子 $\sqrt{d}$$\sqrt d$ 用于避免较大的内积值，尤其是在维度较高的情况下。

3. 因果性（Causality）：由于交互序列的性质，模型在预测第 $(t+1)$$(t+1)$ 个 item 时应该仅考虑前面 $t$$t$ 个 item。然而，time-aware self-attention layer 的第 $t$$t$ 个输出包含所有输入信息。为此，遵从 SASRec，我们通过禁止$j>i$$j\gt i$ 时 ${\overrightarrow{\mathbf{q}}}_i$$\mathbf{\vec q}_i$ 和 ${\overrightarrow{\mathbf{k}}}_j$$\mathbf{\vec k}_j$ 之间的所有链接来修改注意力，其中：

   $${\overrightarrow{\mathbf{q}}}_i={\overrightarrow{\mathbf{m}}}_{s_i}{\mathbf{W}}_Q,{\overrightarrow{\mathbf{k}}}_j={\overrightarrow{\mathbf{m}}}_{s_j}{\mathbf{W}}_K+{\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{i,j}}+{\overrightarrow{\mathbf{p}}}_{K,j}$$

4. Point-Wise Feed-Forward Network：尽管我们的 Time Interval-Aware Self-attention Layer 能够将所有先前的 item、绝对位置、相对时间信息以自适应权重的方式结合起来，但是它是通过线性组合来实现的。在每个 time-aware attention layer 之后，我们应用两个线性变换，这两个线性变换之间有一个 ReLU 非线性激活函数从而赋予模型非线性：

   $$\text{FFN}\left({\overrightarrow{\mathbf{z}}}_i\right)=\text{ReLU}({\overrightarrow{\mathbf{z}}}_i{\mathbf{W}}_1+{\overrightarrow{\mathbf{b}}}_1){\mathbf{W}}_2+{\overrightarrow{\mathbf{b}}}_2$$

   其中：${\mathbf{W}}_1,{\mathbf{W}}_2\in {\mathbb{R}}^{d\times d}$$\mathbf W_1,\mathbf W_2\in \mathbb R^{d\times d}$ 和 ${\overrightarrow{\mathbf{b}}}_1,{\overrightarrow{\mathbf{b}}}_2\in {\mathbb{R}}^d$$\mathbf{\vec b}_1,\mathbf{\vec b}_2\in \mathbb R^d$ 为模型参数。对于同一层的不同 item，这里使用相同的参数（同层之间）；对于不同层的相同 item，这里使用不同的参数（跨层之间）。

   正如 SASRec 所讨论的，在堆叠自注意力层和前馈层之后，会出现更多的问题，包括过拟合、训练过程不稳定（如，梯度消失）、以及需要更多的训练时间。类似于 《Attention Is All You Need》 以及 SASRec，我们也采用 layer normalization、残差连接、以及 dropout 正则化技术来解决这些问题：

   $$\text{LayerNorm}(\overrightarrow{\mathbf{x}})=\overrightarrow{\alpha }\odot \frac{\overrightarrow{\mathbf{x}}-\mu }{\sqrt{{\sigma }^2+ϵ}}+\overrightarrow{\beta }$$

   其中：

   • $\odot$$\odot$ 为逐元素乘积，$\overrightarrow{\alpha }$$\vec\alpha$ 和 $\overrightarrow{\beta }$$\vec \beta$ 分别为待学习的缩放因子和偏置项。

   • $\mu$$\mu$ 和 $\sigma$$\sigma$ 分别为 $\overrightarrow{\mathbf{x}}$$\mathbf{\vec x}$ 的均值和方差，$ϵ$$\epsilon$ 为一个很小的常数项用于防止除以零的错误。

1.1.4 Prediction layer

1. 在堆叠 self-attention block 之后，我们得到了 item, position, time interval 的组合的 representation 。为了预测 next item，我们采用 latent factor model 来计算用户对 item $i$$i$ 的偏好分：

   $${\text{score}}_{i,t+1}={\overrightarrow{\mathbf{z}}}_t\cdot {\overrightarrow{\mathbf{m}}}_i$$

   其中：

   • ${\overrightarrow{\mathbf{m}}}_i$$\mathbf{\vec m}_i$ 为 item $i$$i$ 的 embedding 。

   • ${\overrightarrow{\mathbf{z}}}_t$$\mathbf{\vec z}_t$ 为给定前面 $t$$t$ 个 item （即，$\mathbf{s}=(s_1,s_2,\cdots ,s_t)$$\mathbf s = (s_1,s_2,\cdots,s_{t})$ ）以及它们距离第 $t+1$$t+1$ 个 item 的时间间隔（即，$({\tilde{r}}_{1,t+1},{\tilde{r}}_{2,t+1},\cdots ,{\tilde{r}}_{t,t+1})$$\left(\tilde r_{1,t+1},\tilde r_{2,t+1},\cdots,\tilde r_{t,t+1}\right)$ 的条件下得到的 representation 。

   在每个位置预测的是 next item ，因此是 ${\text{score}}_{i,t+1}$$\text{score}_{i,t+1}$。

1.1.5 模型推断

1. 给定一个时间序列和一个 item 序列，我们定义 $\overrightarrow{\mathbf{o}}=(o_1,o_2,\cdots ,o_n)$$\mathbf{\vec o} = (o_1,o_2,\cdots,o_n)$ 为真实的输出，其中：

   $$\begin{array}{c}{o}_t=\{\begin{array}{ll}\text{<pad>}& \text{if }{s}_{t+1}\text{ is a padding item}\\ s_{t+1}& 1\le t<n\\ {\mathcal{S}}_{|{\mathcal{S}}^{(u)}|}^{(u)}& t=n\end{array}\end{array}$$

   其中：<pad> 表示一个 padding item 。

2. 因为用户交互是隐式反馈数据，我们无法直接优化偏好分数 ${\text{score}}_{i,t+1}$$\text{score}_{i,t+1}$ 。 我们模型的目标是提供一个 ranked item list 。因此，我们采用负采样来优化 item 的排名。对于每个预期的 positive output $o_t$$o_t$ ，我们采样一个 negative item $o_t^{\prime }\notin {\mathcal{S}}^{(u)}$$o_t^\prime \not\in \mathcal S^{(u)}$ 从而生成 pairwise preference orders $\mathcal{D}=\left\{({\mathcal{S}}^{(u)},{\mathcal{T}}^{(u)},o,o^{\prime })\right\}$$\mathcal D=\left\{\left(\mathcal S^{(u)},\mathcal T^{(u)},o,o^\prime\right)\right\}$。

   我们通过 sigmoid 函数 $\sigma (x)=1/(1+\exp (-x))$$\sigma(x) = 1/(1+\exp(-x))$ 将模型输出的偏好分数转换为 0.0 ~ 1.0 之间，并采用二元交叉熵作为损失函数：

   $$\mathcal{J}=-\sum _{{\mathcal{S}}^{(u)}\in \mathbb{S}}\sum _{t\in [1,2,\cdots ,n]}[\log \sigma ({\text{score}}_{o_t,t})+\log (1-\sigma ({\text{score}}_{o_t^{\prime },t}))]+\lambda {\Vert \mathrm{\Theta }\Vert }_F^2$$

   其中：$\mathrm{\Theta }=\{{\mathbf{M}}_I,{\mathbf{M}}_{P,K},{\mathbf{M}}_{P,V},{\mathbf{M}}_{R,K},{\mathbf{M}}_{R,V}\}$$\Theta=\left\{\mathbf M_I, \mathbf M_{P,K},\mathbf M_{P,V},\mathbf M_{R,K},\mathbf M_{R,V}\right\}$为 embedding 矩阵的集合，$||\cdot |{|}_F$$||\cdot||_F$ 为矩阵的 Frobenius 范数，$\lambda$$\lambda$ 为正则化系数。

   注意，我们丢弃了 padding item 的损失。

3. 模型通过 Adam 优化器优化。由于每个训练样本 $({\mathcal{S}}^{(u)},{\mathcal{T}}^{(u)},o,o^{\prime })$$\left(\mathcal S^{(u)},\mathcal T^{(u)},o,o^\prime\right)$ 可以独立构建，因此我们应用 mini-batch SGD 来加快训练效率。

1.2 实验

1. 我们的实验旨在回答以下研究问题：

   • RQ1：我们提出的方法是否在序列推荐中优于 SOTA 的 baseline？

   • RQ2：对于序列推荐，绝对位置或相对时间间隔，哪个更重要？

   • RQ3：超参数如何影响模型性能，如 embedding 维度 $d$$d$ 、序列最大长度 $n$$n$ 、最大时间间隔 $k$$k$ ？

   • RQ4：个性化的时间间隔在这个模型中有用吗？

2. 数据集：我们在六个数据集上评估，这些数据集具有不同的领域、规模、以及稀疏性，并且它们都是可以公开访问的。

   • MovieLens：用于评估协同过滤算法的广泛使用的 benchmark 数据集。我们使用包含 100 万用户评分的版本，即 MovieLens-1M。

   • Amazon：该数据集包含从 Amazon.com 抓取的大量商品评论数据。我们考虑了四个类目，包括 CDs and Vinyl、Movies and TV、Beauty、Video Games 。该数据集高度稀疏。

   • Steam：该数据集是从大型在线视频游戏分发平台 Steam 上抓取的，包含用户的游戏时间、媒体评分、以及开发人员等信息。

   所有这些数据集都包含时间戳或交互的特定日期。

   为了预处理，我们遵循 《Translation-based Recommendation》、SASRec 、FPMC 中的过程：

   • 对于所有数据集，我们将评论或评分视为隐式反馈（即，用户与 item 交互），并按时间戳对 item 进行排序。

   • 对于所有用户，我们在他们自己的序列中减去最小的时间戳，让时间戳从零开始。

   • 我们过滤掉冷启动用户和冷启动 item ，即互动少于 5 次的 user 和互动少于 5 次的 item 。

   • 遵从 SASRec 之后，我们使用最近的 item 用于测试集，使用第二近的 item 用于验证集，剩余的 item 用于训练集。

   数据集的统计结果如下表所示。MovieLens-1m 是最稠密的数据集，具有最长的平均 action 和最少的用户和最少的 item 。Amazon Beauty 和 Amazon Games 具有最短的平均 action 。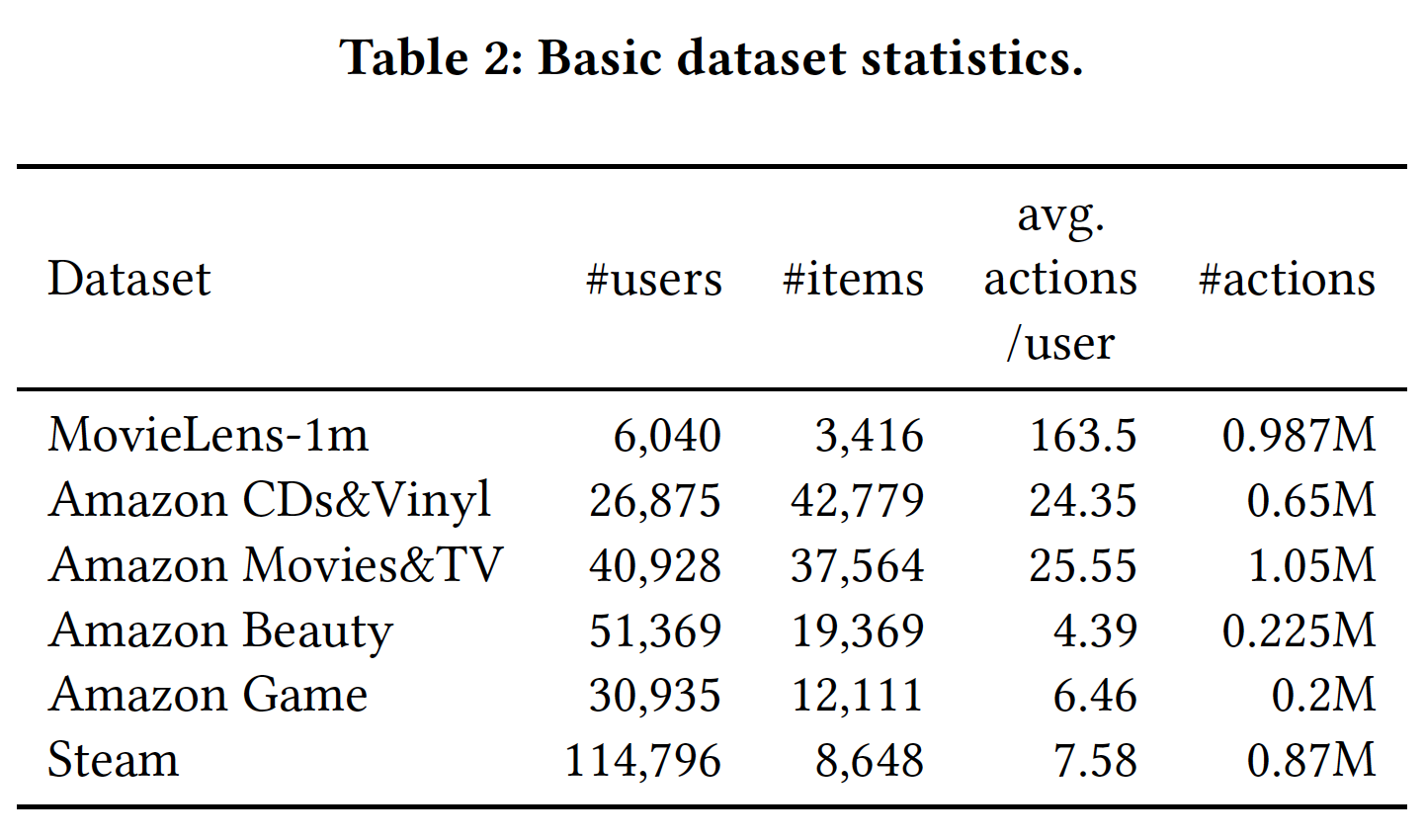

   

3. 评估指标：Hit@10 和 NDCG@10。Hit@10 评估了在 top 10 item list 中有多少比例的 ground-truth item 。NDCG@10 考虑排名信息并将更高的权重分配给更靠前的排名。

   遵从 《Factorization meets the neighborhood: a multifaceted collaborative filtering model》 ，对于每个用户 $u$$u$ ，我们随机采样 100 个 negative item ，并将这些 item 与 ground-truth item 进行排序。我们根据这 101 个 item 的排名来计算 Hit@10 和 NDCG@10 。

4. baseline 方法：

   • 不考虑序列模式的经典的通用推荐（general recommendation）：

     • POP：所有item 根据它们在训练集中的流行度来排序。流行度是根据互动频次来统计的。

     • BPR：贝叶斯个性化排名（bayesian personalized ranking）是通用推荐的经典方法，其中矩阵分解用作推荐器。

   • 基于一阶马尔科夫链的方法：

     • FPMC：该方法结合了矩阵分解和一阶马尔科夫链，分别捕获了长期偏好和动态转移（dynamic transition）。

     • TransRec：该方法将每个用户建模为 item 到 item 的翻译向量（tanslation vector）。这是捕获转移的一阶方法。

   • 基于神经网络的方法：

     • GRU4Rec+：建模用户行为序列从而用于 session-based 推荐。与 GRU4Rec 相比，GRU4Rec+ 采用了不同的损失函数和采样策略，相比于 GRU4Rec 表现出显著的提升。

     • Caser：将最近 item 的序列嵌入到潜在空间的 ”图像“ 中。该方法可以捕获考虑了最近 $L$$L$ 个 item 的高阶马尔科夫链。

     • MARank：最近提出的 SOTA 模型。该方法考虑最近的一些 item 并应用 multi-order attention 来捕获 individual-level 和 union-level 的依赖关系。

     • SASRec 可以视为一种仅考虑绝对位置的方法，将在实验部分与我们的模型进行比较和讨论。

     • 其它序列推荐方法，如 PRME, HRM, Fossil, GRU4Rec 的性能弱于上述 baseline，因此我们省略了与它们的比较。

5. 配置：

   • 为了公平比较，我们使用带 Adam 优化器的 TensorFlow 来实现 BPR, FPMC, TransRec 。对于 GRU4Rec+, Caser, MARank，我们使用作者提供的代码。

   • 我们在 $\{10,20,30,40,50\}$$\{10,20,30,40,50\}$ 中搜索潜在维度，在 $\{{10}^{-4},{10}^{-3},{10}^{-2},{10}^{-1},{10}^0\}$$\left\{10^{-4},10^{-3},10^{-2},10^{-1},10^0\right\}$ 中搜索正则化系数，在 $\{{10}^{-4},{10}^{-3},{10}^{-2},{10}^{-1}\}$$\left\{10^{-4},10^{-3},10^{-2},10^{-1} \right\}$ 中搜索学习率。对于所有其它超参数，我们根据各自的论文使用默认设置。我们使用验证集调优超参数，如果验证集性能在 20 个 epoch 内没有提高，则终止训练。

   • 对于 TiSASRec：

     • 我们使用两层 Time Interval-Aware Self-attention Layer 。

     • 所有数据集的学习率为 0.001，batch size 为 128 ，dropout rate 为 0.2 。

   • 剩余的超参数设置如下表所示。所有实验均使用单个 GTX-1080 Ti GPU 进行。

   

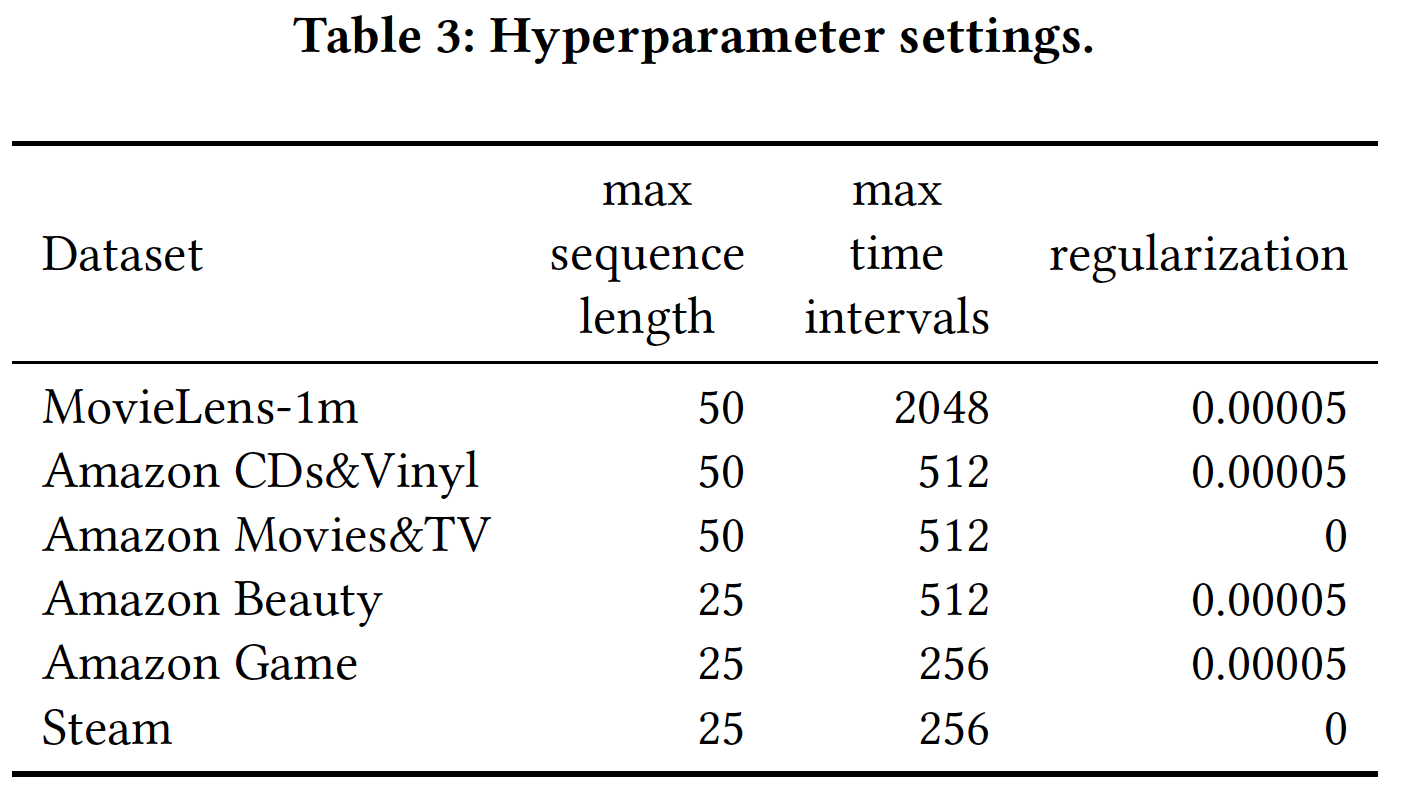
6. 推荐性能（RQ1）：下表给出了所有方法在六个数据集上的推荐性能。可以看到：

   • 在所有 baseline 中，MARank 超越了其它 baseline 。MARank 可以捕获 individual-level 和 union-level 的用户交互，并且很好地处理稀疏数据集。

   • 对于稠密数据集，基于神经网络的方法（即，GRU4Rec+, Caser）比基于马尔科夫链的方法具有显著更好的性能，因为这些方法具有更强的能力来捕获长期序列模式，而这对于稠密数据集很重要。

   • 由于基于马尔科夫链的方法（即，FPMC, TransRec）聚焦于 item 的动态转移，因此它们在稀疏数据集上表现更好。

   • TiSASRec 在所有稠密数据集和稀疏数据集上都超越了所有的 baseline 方法。

   其它方法都没有考虑时间信息，而 TiSASRec 考虑了时间信息，那么这篇论文仅仅证明了时间信息的价值，并不能证明模型架构是好的。为了证明模型架构是好的，论文应该和同时考虑了时间信息的模型去比较。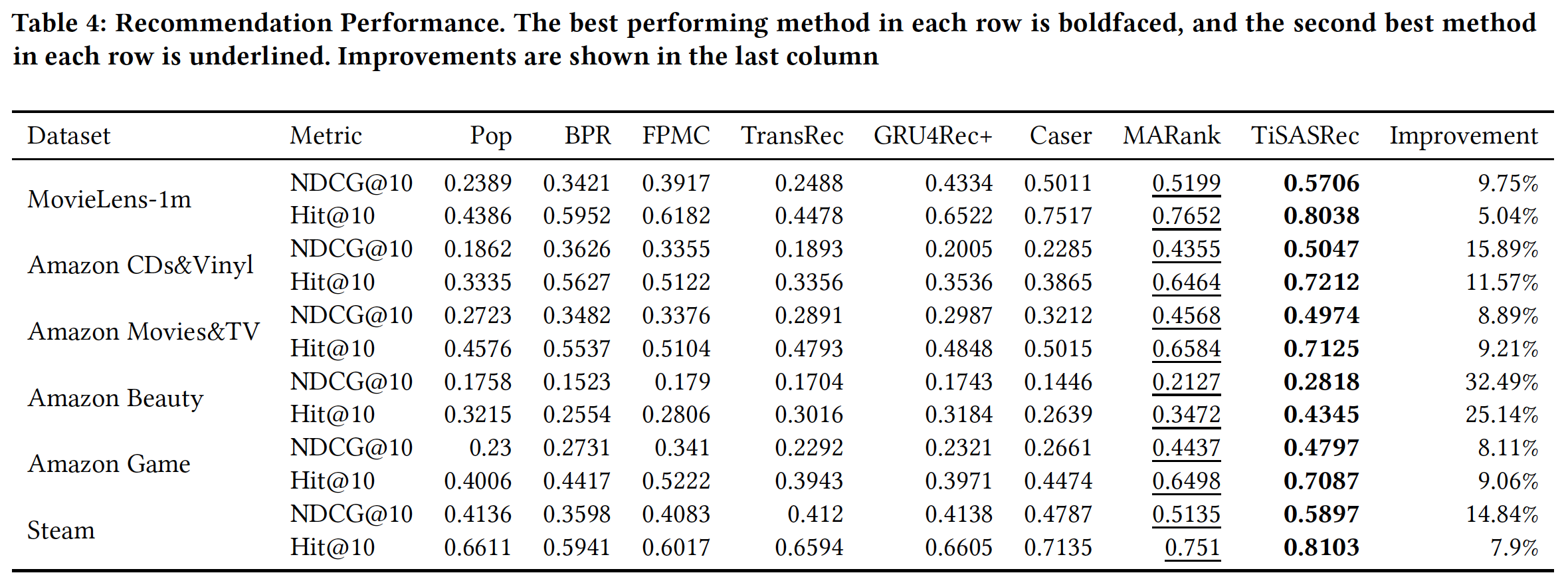

   

7. 相对时间间隔（ RQ2）：为了比较仅有绝对位置、或者仅有相对时间间隔的模型的性能，我们修改Time Interval-Aware Self-attention Layer 的输出 ，使得 TiSASRec 仅考虑相对时间间隔而不考虑绝对位置。具体而言，我们修改Time Interval-Aware Self-attention Layer的输出为：

   $$\begin{array}{c}{\overrightarrow{\mathbf{z}}}_i=\sum _{j=1}^n{\alpha }_{i,j}({\overrightarrow{\mathbf{m}}}_{s_j}{\mathbf{W}}_V+{\overrightarrow{\mathbf{r}}}_{V,{\tilde{r}}_{i,j}})\\ {\alpha }_{i,j}=\frac{\exp (e_{i,j})}{\sum _{j^{\prime }=1}^n\exp (e_{i,j^{\prime }})},e_{i,j}=\frac{\left({\overrightarrow{\mathbf{m}}}_{s_i}{\mathbf{W}}_Q\right){({\overrightarrow{\mathbf{m}}}_{s_j}{\mathbf{W}}_K+{\overrightarrow{\mathbf{r}}}_{K,{\tilde{r}}_{i,j}})}^{\mathrm{\top }}}{\sqrt{d}}\end{array}$$

   即，我们移除了该方程中的 positional embedding ，从而得到一个新的模型，称作 TiSASRec-R 。

   此外，我们将 SASRec 视为一种仅考虑绝对位置的 self-attention 方法。我们在这六个数据集上应用 SASRec, TiSASRec-R, TiSASRec 来比较它们。为公平比较，我们对 SASRec 使用与 TiSASRec 相同的最大序列长度。实验结果如下表所示。可以看到：

   • TiSASRec-R 在 Movie-Lens, CDs&Vinyl, Beauty 数据集上比 SASRec 具有更好的性能，但是在其它三个数据集上则不然。

   • 总体而言，TiSASRec-R （仅使用相对时间间隔）将具有与 SASRec （仅使用绝对位置）相似的性能。

   • 结合了positional embedding 和相对时间间隔 embedding 的 TiSASRec 在所有数据集上超越了 SASRec, TiSASRec-R 。

   限制 TiSASRec-R 性能的主要原因是：用户序列中有许多相同的时间戳。在这种情况下，TiSASRec-R 将在没有任何位置信息的情况下降级为 self-attention 。为了缓解这个问题，我们结合了相对时间间隔和绝对位置。这样，TiSASRec 结合了更丰富的 item 关系来计算注意力权重。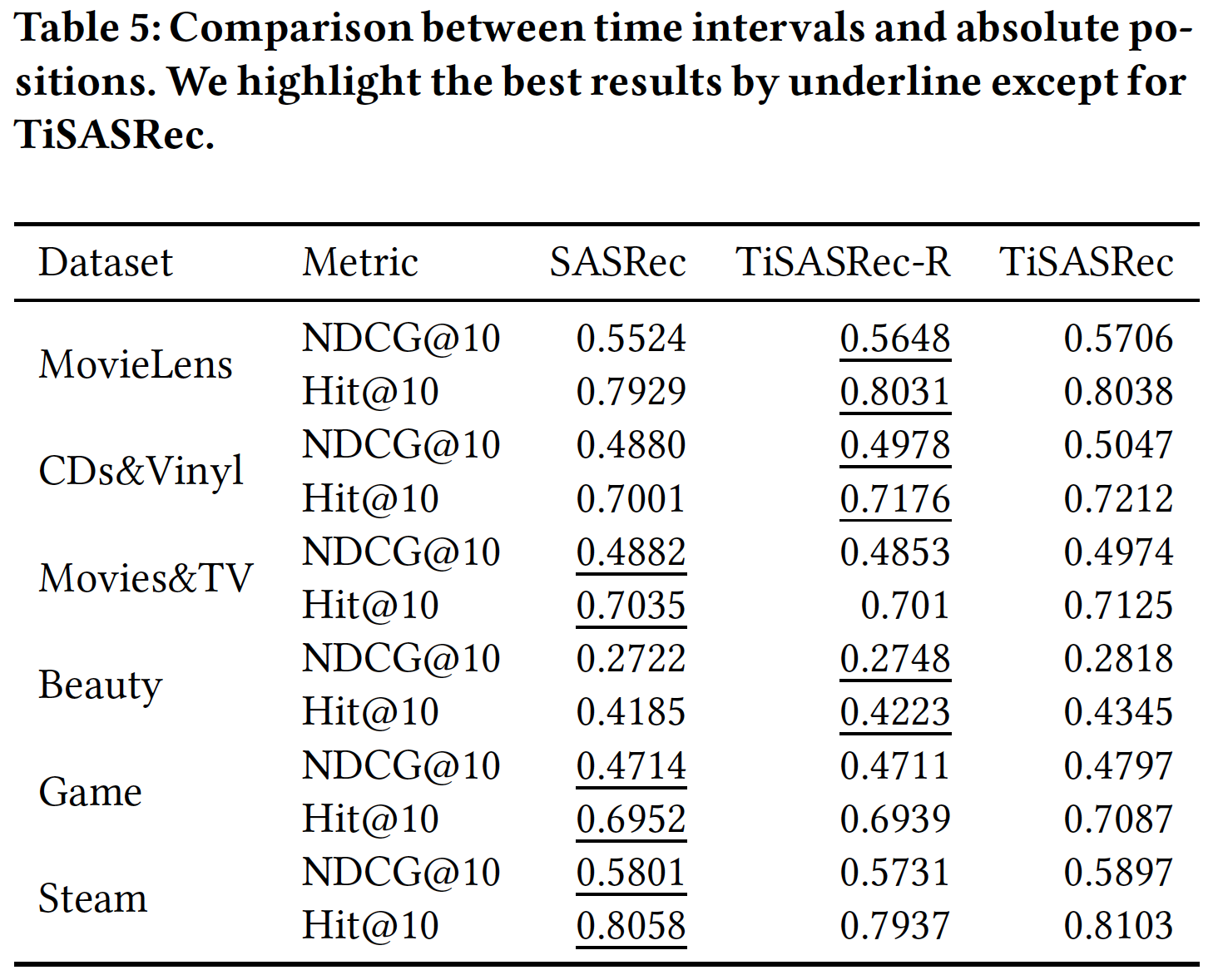

   

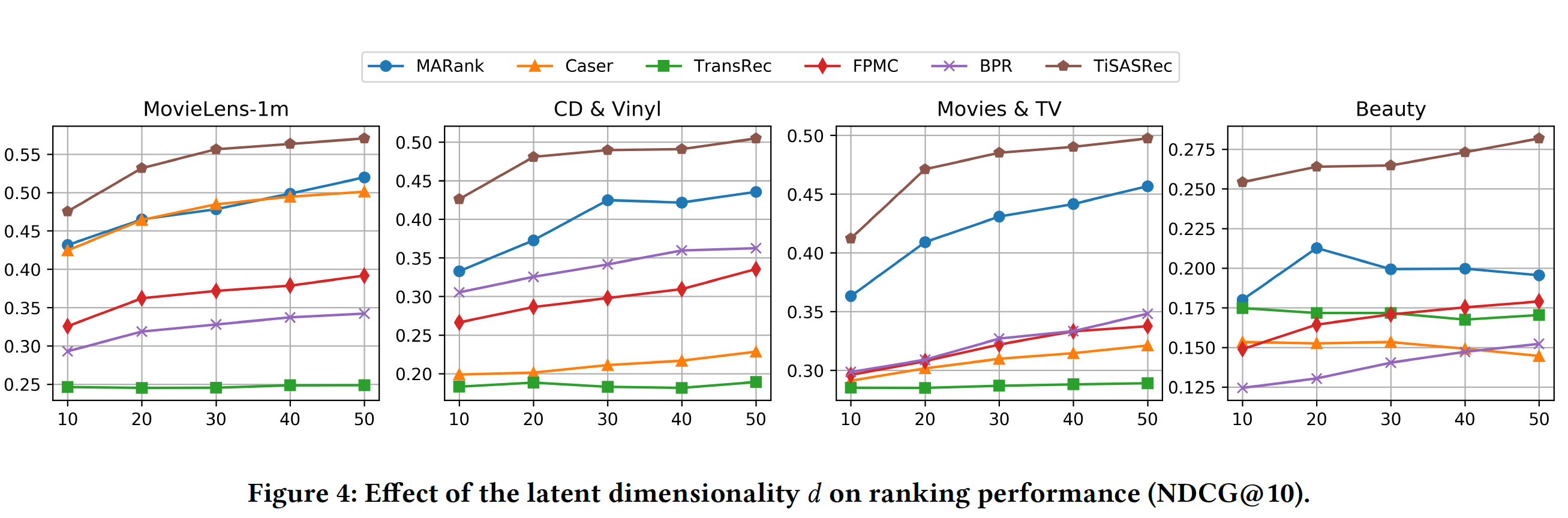
8. 超参数影响（RQ3）：

   • embedding 维度 $d$$d$ ：下图展示了在保持其它最佳超参数不变的情况下，维度 $d$$d$ 从 10 到 50 对 NDCG 指标的影响。可以看到：

     • 在大多数情况下，较大的 $d$$d$ 会导致更好的模型性能。

     • $d$$d$ 的取值对 TransRec 的影响有限。

     • 对于数据集Amazon Beauty，当 $d$$d$ 较大时 Caser, MARank, TransRec 的性能较差。

     

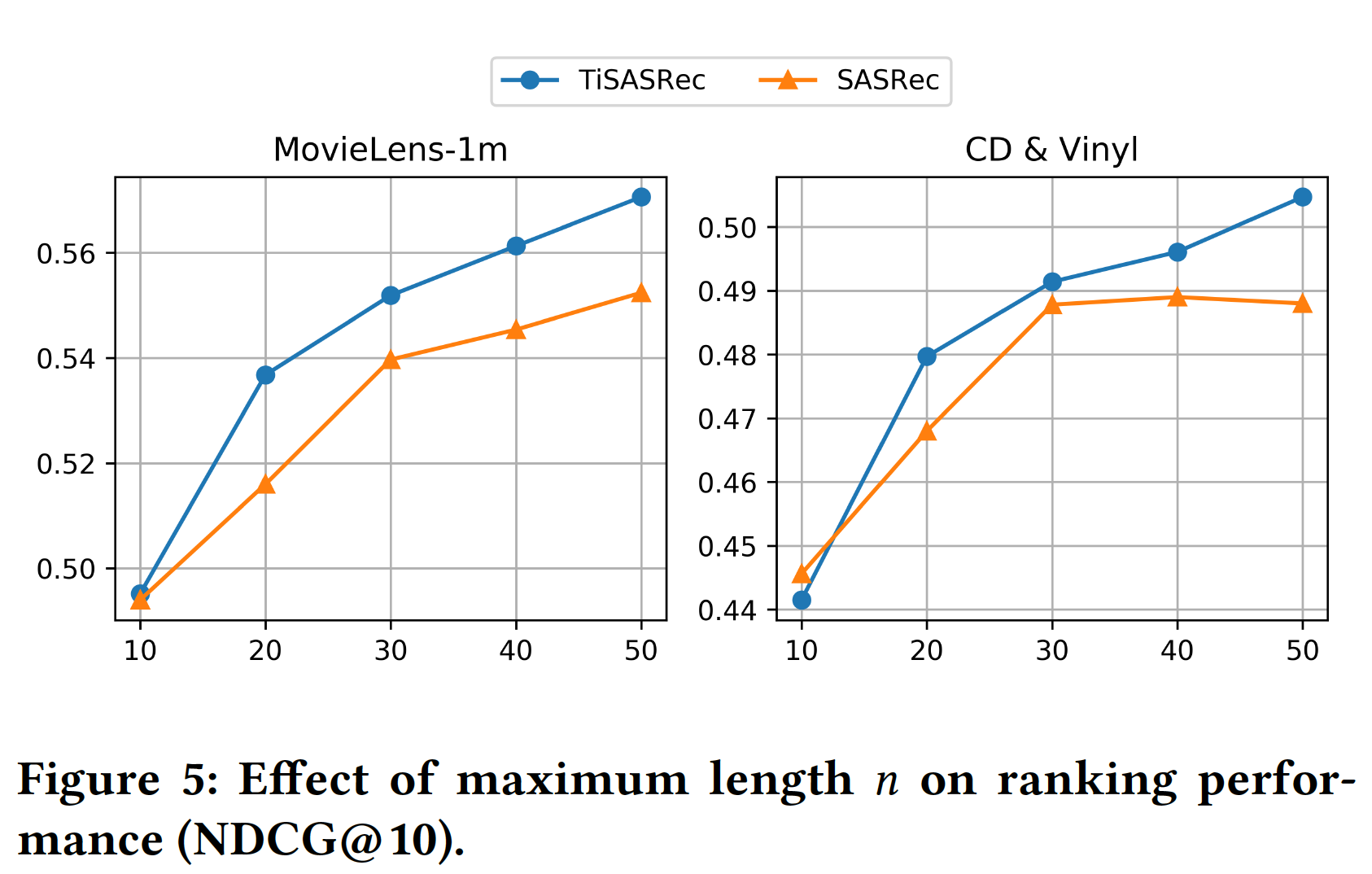
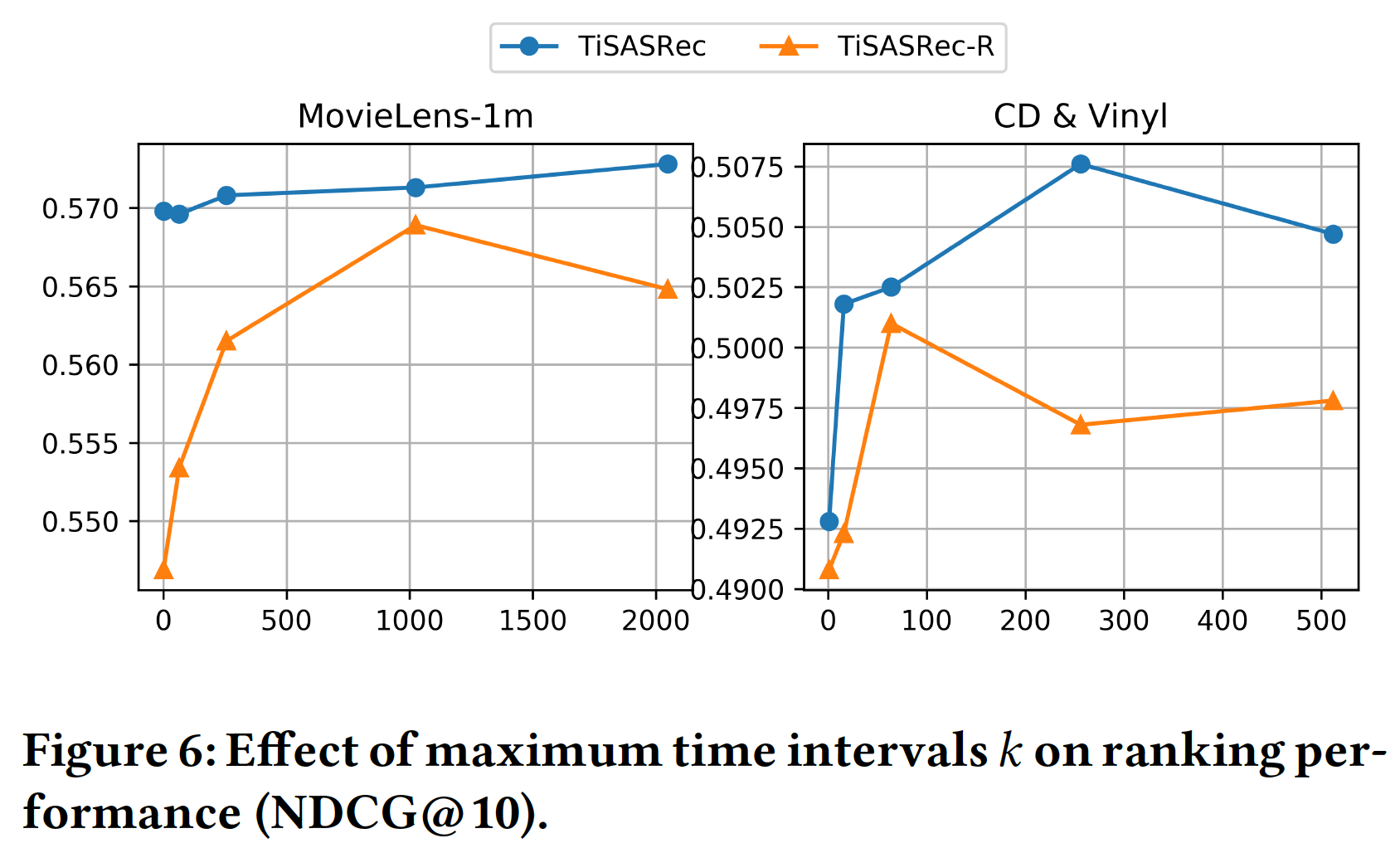
   • 最大序列长度 $n$$n$ ：下图展示了在保持其它最佳超参数不变的情况下，最大序列长度 $n$$n$ 从 10 到 50 对 NDCG 指标的影响。可以看到：更大的 $n$$n$ 导致更好的性能，但是性能的增幅开始变缓。

     

   • 最大时间间隔 $k$$k$ ：下图展示了在保持其它最佳超参数不变的情况下，最大时间间隔 $k$$k$ 对 NDCG 指标的影响。我们为 MovieLens 数据集选择时间间隔 {1, 64, 256, 1024, 2048}，为 Amazon CDs & Vinyl 数据集选择时间间隔 {1, 16, 64, 256, 512} 。可以看到：

     • TiSASRec 在不同的最大时间间隔下具有更稳定的性能。

     • 当 $k$$k$ 正确选择时，TiSASRec-R 实现最佳性能，而对于较大的 $k$$k$ 则变得更差。

     • $k$$k$ 越大则意味着需要训练的模型参数更多。

     

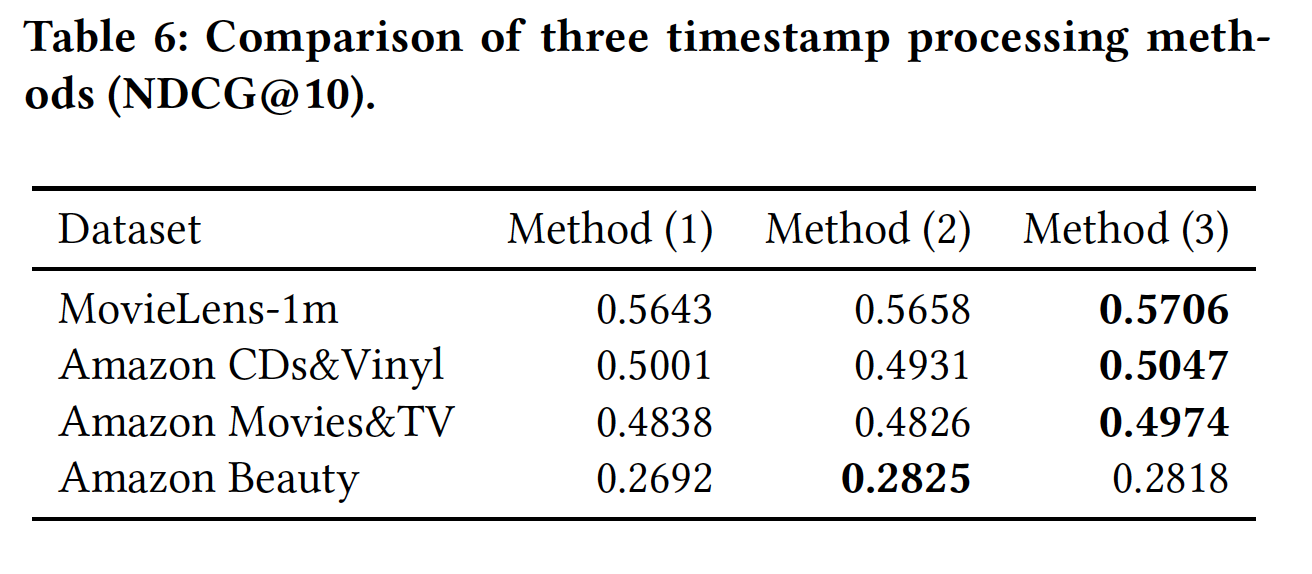
9. 个性化的时间间隔（RQ4）：我们讨论不同的时间戳处理方法，具体而言为以下三种方法：

   • 直接使用时间戳作为特征。我们会减去数据集中最小的时间戳（全局粒度的），让所有时间戳从 0 开始。

   • 使用未缩放的时间间隔。对于每个用户，我们减去序列中的最小时间戳（用户粒度的），让用户的时间戳从 0 开始。

   • 使用个性化的时间间隔。对于每个用户，我们减去序列中的最小时间戳（用户粒度的），然后除以该序列的最小时间间隔。

   下表给出了时间戳不同处理方法的结果。注意，我们不会在前两种方法中裁剪时间戳。可以看到：第三种方法（即，个性化的时间间隔）在前三个数据集中获得了最佳性能。

   

10. 可视化：我们使用 TiSASRec 来预测用户可能交互的 next item。然后，我们将所有时间间隔设为相同从而获得另一个预测。如下图所示，可以看到时间间隔影响了预测结果。

    

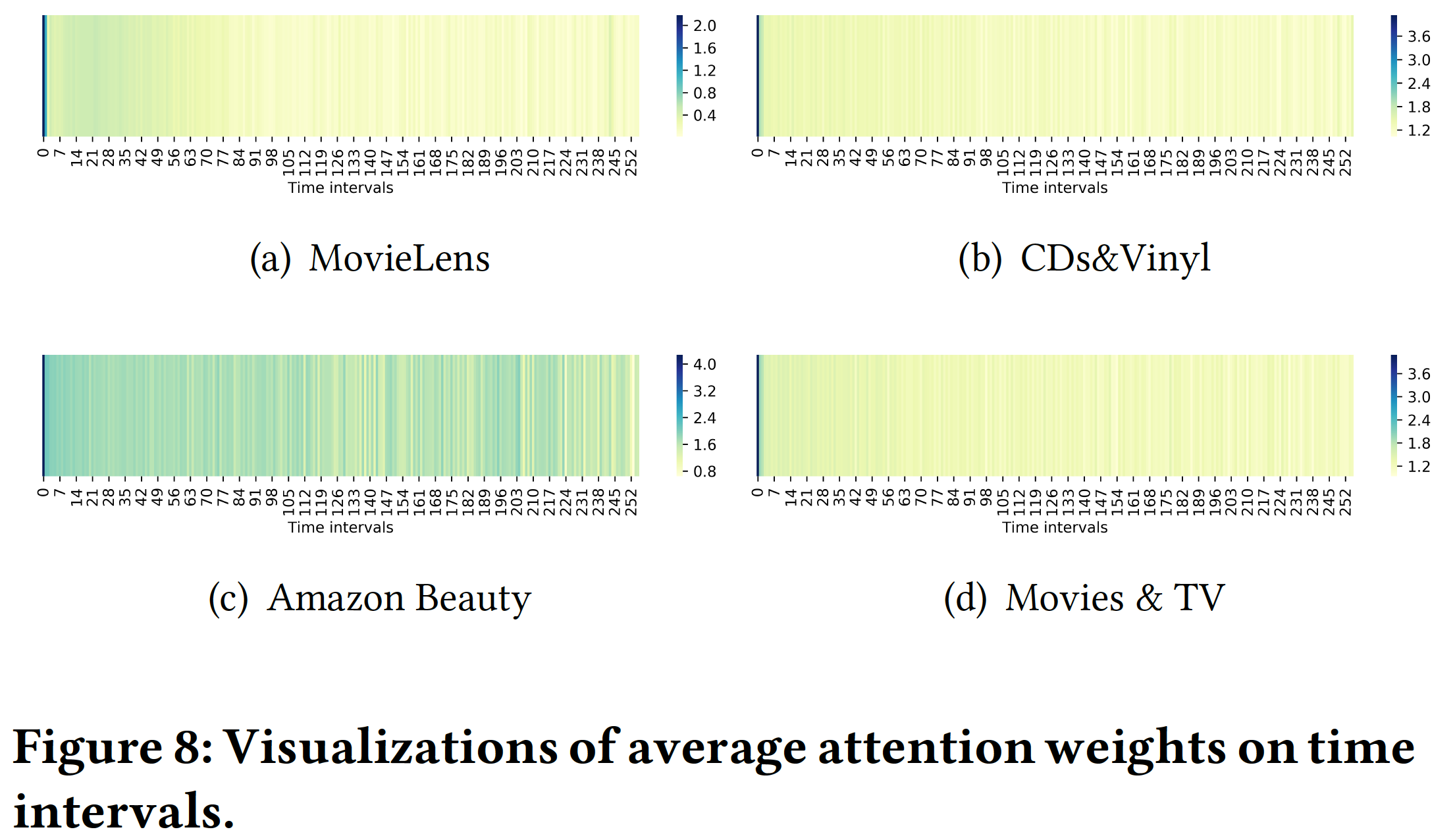
    下图展示了前 256 个时间间隔的平均注意力权重 ${\alpha }_{i,j}$$\alpha_{i,j}$ 的四个热力图（$|i-j|$$|i-j|$ 作为时间间隔）。注意，我们在计算平均权重时，分母是有效权重的个数，从而避免短序列中 padding item 的影响。从这四个热力图中我们可以看到：

    • 小的时间间隔通常比大的时间间隔具有更大的权重，这意味着最近的 item 对 next item 的预测具有更大的影响。

    • 稠密数据集（如 MovieLens）比稀疏数据集（如CDs&Vinyl ）需要更大范围的 item （即，间隔更大），因为 MovieLens 热力图左侧有一个较大的绿色区域同时右侧是黄色区域。

    • Amazon Beauty 数据集的热力图没有明显的绿色区域或黄色区域，可能是因为该数据集没有明显的序列模式。这就解释了为什么几种序列方法在这个数据集上表现不佳。