一、FMLP-Rec [2022]

《Filter-enhanced MLP is All You Need for Sequential Recommendation》

1. 近来，循环神经网络（RNN）、卷积神经网络（CNN）和 Transformer 等深度神经网络已被应用于序列推荐任务中，该任务旨在从记录的用户行为数据中捕获动态的偏好特性，以实现精准推荐。然而，在在线平台中，记录的用户行为数据不可避免地包含噪声，深度推荐模型很容易在这些数据上发生过拟合。为解决这一问题，我们借鉴了信号处理中滤波算法的思想，在频域中对噪声进行衰减。在实证实验中，我们发现滤波算法能显著提升具有代表性的序列推荐模型的性能，将简单的滤波算法（如带阻滤波器 Band-Stop Filter ）与 all-MLP 架构相结合，甚至能超越 Transformer-based 的竞争模型。受此启发，我们提出了 FMLP-Rec，这是一种用于序列推荐任务的、带有可学习滤波器的 all-MLP 模型。all-MLP 架构使我们的模型具有更低的时间复杂度，可学习滤波器能够自适应地在频域中衰减噪声信息。在八个真实数据集上进行的大量实验表明，我们提出的方法优于基于 RNN、CNN、GNN 和 Transformer 的竞争方法。我们的代码和数据可在以下链接公开获取：https://github.com/RUCAIBox/FMLP-Rec。

2. 推荐系统已广泛应用于在线平台（如亚马逊和淘宝），用于在大量 items 中预测用户的潜在兴趣。在实际应用中，用户行为随时间动态变化。因此，捕获用户行为的序列特征以进行合适的推荐至关重要，这也是序列推荐的核心目标。

   为了刻画用户历史行为的演变模式，文献中基于深度神经网络开发了许多序列推荐模型。典型的解决方案基于 RNN 和 CNN。此外，大量研究采用更先进的神经网络架构（如 memory network 和自注意力机制）来增强建模能力，以便更有效地捕获动态的用户偏好。最近，基于 Transformer 的方法通过堆叠 multi-head self-attention layers ，在该任务中表现出卓越的性能。

   • 然而，堆叠的自注意力层涉及大量参数，这可能导致基于 Transformer 的方法出现过参数化（over-parameterized）的问题。

   • 此外，这些方法主要根据记录的用户行为数据来拟合模型参数，而这些数据本质上存在噪声，甚至可能包含恶意伪造的数据。研究发现，深度神经网络容易在含噪声的数据上发生过拟合。当记录的序列数据包含噪声时，基于自注意力的推荐器的过拟合问题会更加严重，因为它在进行序列建模时会关注所有 items 。

   考虑到上述问题，我们旨在简化基于 Transformer 的序列推荐器，并提高其对记录数据中噪声的鲁棒性。我们的核心思想借鉴自数字信号处理领域，在该领域中，滤波算法用于降低噪声对序列数据的影响。我们推测，对序列数据进行降噪后，捕获用户的序列行为会变得更容易。如果这一推测成立，我们或许能够简化基于 Transformer 方法中的 heavy 的自注意力组件。为验证这一假设，我们在论文中进行了一些实证实验，通过三种经典滤波算法对 item embeddings 进行简单的降噪（更多细节见 Table 1）。我们发现，滤波算法能够显著提升这些深度序列推荐模型的性能，包括基于 Transformer 的 SASRec 模型。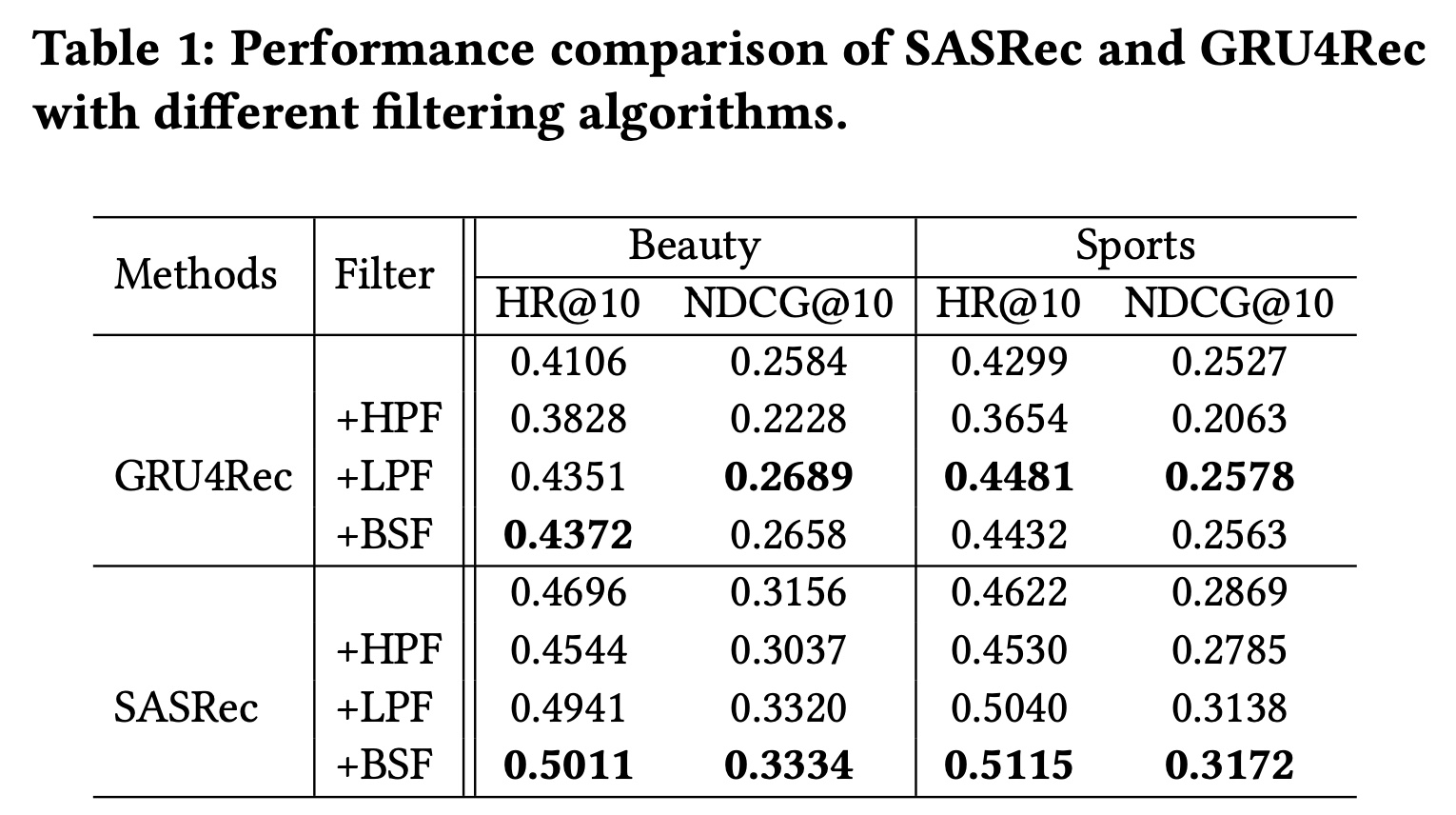

   

   受实证结果的启发，我们提出了一种新颖的 Filter-enhanced MLP approach for sequential Recommendation ，名为 FMLP-Rec 。通过去除 Transformer 中的自注意力组件，FMLP-Rec 完全基于 MLP 结构来堆叠模块。作为主要技术贡献，我们在每个 stacked block 中融入了一个 filter 组件，在该组件中，我们执行快速傅里叶变换（Fast Fourier Transform: FFT）将 input representations 转换到频域，然后通过 inverse FFT 过程恢复 denoised representations。filter 组件在减少 item representations 中的噪音的影响方面起着关键作用。为实现这一点，我们引入 learnable filters 在频域中对 input item sequences 进行编码，这些 filters 可以从原始数据中进行优化，无需人工先验知识。我们的方法能够有效衰减噪声信息，并从所有频率（如长期的 / 短期的 item interactions ）中提取有意义的特征。从理论上讲，根据卷积定理可以证明，learnable filters 在时域中相当于循环卷积（circular convolution），在整个序列上具有更大的感受野，能够更好地捕获用户行为的周期性的特性。filter 组件的另一个优点是：在不考虑 pairwise item correlations 的情况下，它所需的时间成本更低，从而形成了一个更轻量、更快的网络架构。

   据我们所知，这是首次将 filter-enhanced all-MLP 架构应用于序列推荐任务，该架构简单、有效且高效。为验证我们模型的有效性，我们在来自不同场景的八个真实数据集上进行了广泛的实验，用于序列推荐。实验结果表明，FMLP-Rec 在性能上优于 SOTA 的基于 RNN、CNN、GNN 和 Transformer 的基线模型。

1.1 预备知识

1. 在本节中，我们阐述序列推荐问题，并介绍离散傅里叶变换。

2. 问题陈述：假设我们有一组用户和一组 items ，分别用 $\mathcal{U}$$\mathcal U$ 和 $\mathcal{I}$$\mathcal I$ 来表示，其中 $u\in \mathcal{U}$$u\in \mathcal U$ 表示一个用户， $i\in \mathcal{I}$$i\in \mathcal I$ 表示一个 item 。用户和 items 的数量分别用 $|\mathcal{U}|$$|\mathcal U|$ 和 $|\mathcal{I}|$$|\mathcal I|$ 来表示。对于具有隐式反馈的序列推荐，用户 $u$$u$ 有一个context $\mathbf{c}$$\mathbf c$ ，即按时间顺序排列的 items 的交互序列：$\mathbf{c}=\{i_1,\cdots ,i_n\}$$\mathbf c=\{i_1,\cdots,i_n\}$，其中 $n$$n$ 是交互次数，$i_t$$i_t$ 是用户 $u$$u$ 交互的第 $t$$t$ 个 item 。为方便起见，我们用 ${\mathbf{i}}_{j:k}$$\mathbf i_{j:k}$ 表示子序列，即 ${\mathbf{i}}_{j:k}=\{i_j,\cdots ,i_k\}$$\mathbf i_{j:k} = \{i_j,\cdots,i_k\}$，其中 $1\le j<k\le n$$1\le j\lt k\le n$。

   基于上述符号，我们现在定义序列推荐任务。正式地，给定用户的上下文 item sequence $\mathbf{c}=\{i_1,\cdots ,i_n\}$$\mathbf c = \{i_1,\cdots,i_n\}$ ，序列推荐任务是预测用户在第 $(n+1)$$(n+1)$ 步可能交互的 next item ，表示为 $p(i_{n+1}\mid {\mathbf{i}}_{1:n})$$p(i_{n+1}\mid \mathbf i_{1:n})$。

3. 傅里叶变换：离散傅里叶变换（Discrete Fourier transform: DFT ）在数字信号处理领域至关重要，也是我们方法的关键组成部分。在本文中，我们仅考虑一维 DFT 。给定 numbers 的一个序列 $\{x_n\}$$\{x_n\}$，其中 $0\le n\le N-1$$0\le n\le N-1$ ，一维 DFT 通过以下公式将序列转换到频域：

   $$X_k=\sum _{n=0}^{N-1}{x}_n\times \exp (-\frac{2\pi i}{N}nk),0\le k\le N-1$$

   其中 $i$$i$ 是虚数单位。

   对于每个 $k$$k$ ，DFT 生成一个新的 representation $X_k$$X_k$ ，它是所有原始 input tokens $x_n$$x_n$ 与所谓的 “旋转因子” 的总和。这样，$X_k$$X_k$ 表示序列 $\{x_n\}$$\{x_n\}$ 在频率 ${\omega }_k=2\pi k/N$$\omega_k = 2\pi k/N$ 处的频谱。注意，DFT 是一种一一变换。给定 DFT ，我们可以通过 inverse DFT （IDFT）恢复原始序列 ：

   $$x_n=\frac{1}{N}\sum _{k=0}^{N-1}{X}_k\exp \left(\frac{2\pi i}{N}nk\right)$$

4. 快速傅里叶变换：为计算 DFT，快速傅里叶变换（Fast Fourier Transform: FFT）在先前研究中被广泛使用。标准的 FFT 算法是 Cooley- Tukey 算法，它递归地重新表达长度为 $N$$N$ 的序列的 DFT，并将时间复杂度降低到 $O(N\log N)$$O(N\log N)$ 。IDFT 与 DFT 形式相似，也可以使用逆快速傅里叶变换（inverse fast Fourier transform: IFFT）高效计算。

   由于 FFT 可以将输入信号转换到频域，在频域中更容易捕获周期性特征，因此它在数字信号处理领域被广泛用于过滤噪声信号。一种常用的方法是低通滤波器（Low-Pass Filter: LPF），它在经过 FFT 处理后衰减高频噪声信号。在本文中，我们考虑使用 FFT 和滤波算法来减少用户交互项目序列中噪声特征的影响。

1.2 基于滤波算法的推荐实证分析

1. 在本节中，我们进行实证研究，以测试：

   • (1)：滤波算法在序列推荐模型中的有效性。

   • (2)：将滤波算法与 all-MLP 架构相结合的有效性。

1.2.1 分析设置

1. 在实证研究中，我们选 Amazon Beauty and Sports 数据集来评估序列推荐方法。

2. 序列推荐算法：我们在 GRU4Rec 和 SASRec 这两个具有代表性的序列推荐模型上进行实验。这两个模型在很大程度上遵循深度序列模型的标准框架，由 embedding layer 、sequence encoder layer 和 prediction layer 组成，但在 sequence encoder layer 分别采用 RNN 和 Transformer。尽管这两个模型已显示出有前景的结果，但它们可能对用户行为序列中的噪声缺乏鲁棒性。因此，我们直接在这两个模型的 embedding layer 和 sequence encoder layer 之间添加一个无参数的 filter layer ，且不改变其他组件。

3. 滤波算法：在 filter layer 中，给定 item sequence 的 embedding 矩阵，我们对特征的每个维度执行以下操作： FFT -> Filtering Algorithm -> IFFT 。滤波后，我们将 denoised embedding matrix 作为 sequence encoder layer 的输入。对于滤波算法，我们选择以下三种经典方法：

   • 高通滤波器（High-Pass Filter: HPF ）：高通滤波器允许高频信号通过，衰减低频信号。在 FFT 之后，我们将信号低频部分的值设置为零。

   • 低通滤波器（Low-Pass Filter: LPF）：低通滤波器允许低频信号通过，衰减高频信号。在 FFT 之后，我们将信号高频部分的值设置为零。

   • 带阻滤波器（Band-Stop Filter: BSF）：带阻滤波器衰减中频信号，让其他信号通过。在 FFT 之后，我们将信号中频部分的值设置为零。

1.2.2 结果与发现

1. 在本部分，我们展示结果并讨论发现。

2. 对代表性模型的影响：我们在 Table 1 中报告结果。可以看出：

   • 添加低通滤波器（LPF）和带阻滤波器（BSF）会带来一致的性能提升，尤其是在 SASRec 模型上。对于 GRU4Rec，LPF 比其他滤波算法实现了最佳性能，而对于 SASRec，BSF 表现最佳。

   • 相比之下，高通滤波器（HPF ）在大多数情况下导致性能下降。

   从这些观察结果，我们可以得出以下结论：

   • item embedding matrix 可能包含影响序列推荐模型性能的噪声。

   • 在 embedding layer 使用合适的滤波算法有助于缓解上述问题。但对于不同的模型，最合适的滤波算法可能也不同。

   • embedding matrix 中的低频信息对于序列推荐似乎更为重要。这一现象与水文学、地震学和行为学中的发现类似，即自然和人类行为中的低频信号通常是有意义的周期性特征。

   

3. 对 all-MLP 模型的影响：上述研究证实，滤波算法可以提高基于 RNN 和基于 Transformer 的序列推荐模型的性能。在本部分，我们继续检验将这些滤波算法与 all-MLP 架构相结合的简单变体模型的性能。基于 SASRec 的架构，我们移除 Transformer-based sequence encoder layer 中的 multi-head self-attention blocks ，但在 embedding layer 之后添加一个 filter layer 。我们也选择 HPF、LPF 和 BSF 算法，其他组件保持不变。这样，变体模型仅依靠 MLP 对 item sequence 进行建模。

   我们在 Figure 1 中报告基于 SASRec 的 all-MLP 变体模型的性能。可以看到：

   • 移除 multi-head self-attention blocks 后，大多数模型变体仍然表现良好。

   • 带有 LPF 的变体模型甚至在很大程度上优于 SASRec 模型。这表明合适的滤波算法可以激发简单 all-MLP 模型的潜力，使其超越复杂的 Transformer-based 的模型。

   通过去除噪声信息和 self-attention blocks ，模型更加轻量，降低了过拟合的风险。基于上述分析，设计一种带有合适滤波算法的有效且高效的 all-MLP 模型用于序列推荐是很有前景的。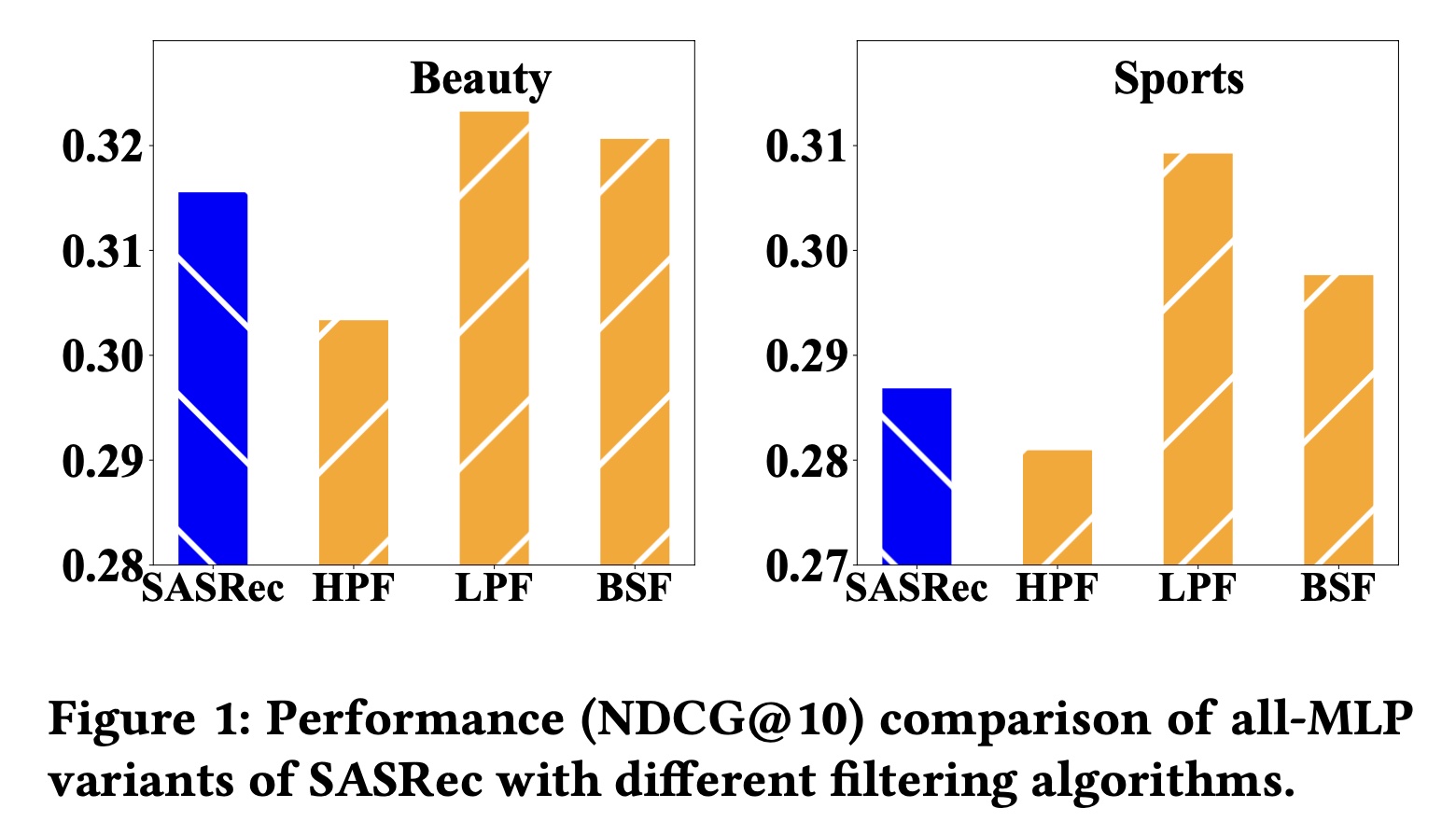

   

1.3 方法

1. 前面的实证结果表明，带有合适滤波算法（如 LPF）的 all-MLP 架构可以产生非常好的推荐性能。然而，以前的滤波算法通常需要领域知识或专家的努力来设计合适的滤波器并设置超参数（如滤波阈值）。如何有效地将滤波算法集成到现有的深度推荐框架中仍然是一个挑战。在本节中，我们提出一种用于序列推荐的 all-MLP 架构（名为 FMLP-Rec），它通过堆叠带有 learnable filters 的 MLP blocks ，能够针对各种序列推荐场景自动学习合适的滤波器。

1.3.1 FMLP-Rec

1. 与原始 Transformer 架构类似，我们的 FMLP-Rec 也堆叠多个 neural blocks ，以生成用户序列偏好的 representation 从而用于推荐。我们方法的关键区别在于，用一种新颖的滤波器结构取代了 Transformer 中的多头自注意力结构。除了滤波器的噪声衰减作用外，这种结构在数学上等效于循环卷积（在后续章节中证明），也能够捕获序列级偏好。接下来，我们详细介绍我们的方法。

   注意：下图中，有些 dropout 操作并未画出来。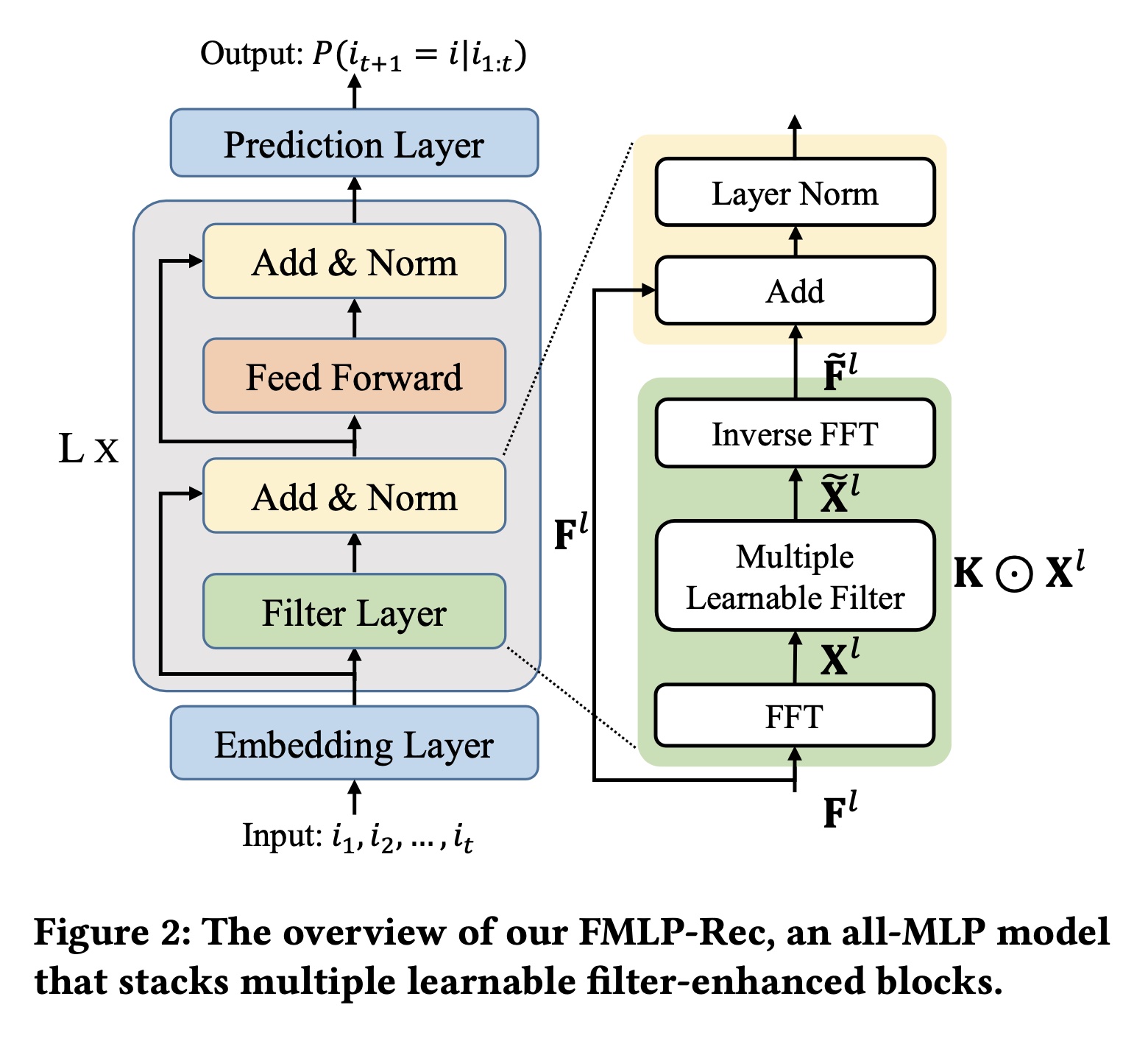

   

2. Embedding Layer ：在 embedding layer ，我们维护一个 item embedding matrix ${\mathbf{M}}_I\in {\mathbb{R}}^{|\mathcal{I}|\times d}$$\mathbf M_I\in \mathbb R^{|\mathcal I|\times d}$ ，将 item 的高维 one-hot representation 投影到低维 dense representation。给定一个长度为 $n$$n$ 的 item sequence ，我们从 ${\mathbf{M}}_I$$\mathbf M_I$ 中进行 look-up 操作，形成 input embedding matrix $\mathbf{E}\in {\mathbb{R}}^{n\times d}$$\mathbf E\in \mathbb R^{n\times d}$。此外，我们引入一个可学习的 position encoding matrix $\mathbf{P}\in {\mathbb{R}}^{n\times d}$$\mathbf P\in \mathbb R^{n\times d}$，以增强 item sequence的 input representation 。通过这种方式，sequence representation ${\mathbf{E}}_I\in {\mathbb{R}}^{n\times d}$$\mathbf E_I\in \mathbb R^{n\times d}$ 可以通过将两个 embedding matrices 相加得到。

   由于 item embedding matrix 和 position encoding matrix 都是随机初始化的，这可能会影响滤波机制并导致训练过程不稳定。受近期研究的启发，我们执行 dropout 和 layer normalization 操作来缓解这些问题。因此，我们通过以下公式生成 sequence representation ${\mathbf{E}}_I\in {\mathbb{R}}^{n\times d}$$\mathbf E_I\in \mathbb R^{n\times d}$ ：

   $${\mathbf{E}}_I=\text{Dropout}(\text{LayerNorm}(\mathbf{E}+\mathbf{P}))$$

3. Learnable Filter-enhanced Blocks ：基于 embedding layer ，我们通过堆叠多个 learnable filter blocks 来开发 item encoder 。一个 learnable filter block 通常由两个子层组成，即 filter layer 和 point-wise feed-forward network。

   • Filter Layer ：在 filter layer ，我们在频域中对特征的每个维度执行滤波操作，然后进行 skip connection 和 layer normalization 。

     • 给定第 $l$$l$ 层的 input item representation matrix ${\mathbf{F}}^l\in {\mathbb{R}}^{n\times d}$$\mathbf F^l\in \mathbb R^{n\times d}$（当 $l=0$$l=0$ 时，我们设置 ${\mathbf{F}}^0={\mathbf{E}}_I$$\mathbf F^0 = \mathbf E_I$ ），我们首先沿 item 维度执行 FFT，将 ${\mathbf{F}}^l$$\mathbf F^l$ 转换到频域：

       $${\mathbf{X}}^l=\mathcal{F}\left({\mathbf{F}}^l\right)\in {\mathbb{C}}^{n\times d}$$

       其中：$\mathcal{F}(\cdot )$$\mathcal F(\cdot)$表示一维 FFT。注意，${\mathbf{X}}^l$$\mathbf X^l$ 是一个复张量，表示 ${\mathbf{F}}^l$$\mathbf F^l$ 的频谱。

       对于 embedding 的 $d$$d$ 个维度，对每个维度分别进行一维 FFT 。

     • 然后，我们通过乘以一个 learnable filter $\mathbf{W}\in {\mathbb{C}}^{n\times d}$$\mathbf W\in \mathbb C^{n\times d}$ 来调制频谱：

       $${\tilde{\mathbf{X}}}^l=\mathbf{W}\odot {\mathbf{X}}^l$$

       其中：$\odot$$\odot$ 是逐元素乘法。滤波器 $\mathbf{W}$$\mathbf W$ 被称为 learnable filter ，因为它可以通过随机梯度下降（SGD）进行优化，以在频域中自适应地表示任意滤波器。

       注意，这里的 $\mathbf{W}$$\mathbf W$ 定义在复数域，而不是实数域。

     • 最后，我们采用 IFFT 将调制后的频谱 $\tilde{\mathbf{X}}$$\tilde{\mathbf X}$ 转换回时域，并更新 sequence representations ：

       $${\tilde{\mathbf{F}}}^l\leftarrow {\mathcal{F}}^{-1}\left({\tilde{\mathbf{X}}}^l\right)\in {\mathbb{R}}^{n\times d}$$

       其中：${\mathcal{F}}^{-1}(\cdot )$$\mathcal F^{-1}(\cdot)$ 表示逆一维 FFT，它将复张量转换为实数值张量。

     通过 FFT 和 IFFT 操作，可以有效降低记录数据中的噪声，从而获得更纯净的 item embeddings。遵循 SASRec，我们还结合skip connection 、layer normalization 和 dropout 操作，以缓解梯度消失和训练不稳定的问题：

     $${\tilde{\mathbf{F}}}^l=\text{LayerNorm}({\mathbf{F}}^l+\text{Dropout}\left({\tilde{\mathbf{F}}}^l\right))$$

   • Feed-forward layers ：在 point-wise feed-forward network中，我们结合 MLP 和 ReLU 激活函数，进一步捕获非线性。计算定义如下：

     $$\text{FFN}\left({\tilde{\mathbf{F}}}^l\right)=\left(\text{ReLU}({\tilde{\mathbf{F}}}^l{\mathbf{W}}_1+{\overrightarrow{\mathbf{b}}}_1)\right){\mathbf{W}}_2+{\overrightarrow{\mathbf{b}}}_2$$

     其中 ${\mathbf{W}}_1,{\overrightarrow{\mathbf{b}}}_1,{\mathbf{W}}_2,{\overrightarrow{\mathbf{b}}}_2$$\mathbf W_1,\mathbf{\vec b}_1,\mathbf W_2,\mathbf{\vec b}_2$ 是可训练参数。

     然后，我们也执行 skip connection 和 layer normalization 和操作，以生成第 $l$$l$ 层的输出。

     即，${\mathbf{F}}^l=\text{LayerNorm}({\tilde{\mathbf{F}}}^l+\text{FFN}\left({\tilde{\mathbf{F}}}^l\right))$$\mathbf F^l = \text{LayerNorm}\left(\tilde{\mathbf F}^l + \text{FFN}\left(\tilde{\mathbf F}^l\right) \right)$

4. Prediction Layer ：在 FMLP-Rec 的 final layer ，我们计算在用户历史的 context 下，用户在 step $(t+1)$$(t+1)$ 对 item $i$$i$ 的偏好得分：

   $$P(i_{t+1}=i\mid {\mathbf{i}}_{1:t})={\overrightarrow{\mathbf{e}}}_i^{\mathrm{\top }}{\overrightarrow{\mathbf{f}}}_t^L$$

   其中：

   • ${\overrightarrow{\mathbf{e}}}_i$$\mathbf{\vec e}_i$ 是 item embedding matrix ${\mathbf{M}}_I$$\mathbf M_I$ 中 item $i$$i$ 的 representation 。

   • ${\overrightarrow{\mathbf{f}}}_t^L$$\mathbf {\vec f}_t^L$ 是 L-layer learnable filter blocks 在 step $t$$t$ 的输出， $L$$L$ 是 learnable filter blocks 的数量。它就是 ${\mathbf{F}}^L$$\mathbf F^L$ 的第 $t$$t$ 行。

   我们采用 pairwise rank loss 来优化模型参数：

   $$L=-\sum _{u\in \mathcal{U}}\sum _{t=1}^n\log \sigma (P(i_{t+1}\mid {\mathbf{i}}_{1:t})-P(i_{t+1}^{-}\mid {\mathbf{i}}_{1:t}))$$

   其中，我们将每个 ground-truth item $i_{t+1}$$i_{t+1}$ 与一个随机采样的 negative item $i_{t+1}^{-}$$i_{t+1}^-$ 进行配对。

1.3.2 Filter Layers 的理论分析

1. 除了降噪功能外，我们现在证明所提出的 filter blocks 也能够从记录的数据中捕获 sequential characteristics 。我们首先从理论上证明我们提出的 learnable filter 等效于循环卷积。

2. 在 FMLP-Rec 的 filter layer 中，输入信息首先通过 FFT 转换到频域的 spectrum representations，然后与 learnable filter $\mathbf{W}$$\mathbf W$ 相乘。这样，learnable filter $\mathbf{W}$$\mathbf W$ 的公式可以看作是针对 item embedding matrix 中不同 hidden dimensions 的一组可学习的频率滤波器 $\{{\overrightarrow{\mathbf{w}}}^{(1)},\cdots ,{\overrightarrow{\mathbf{w}}}^{(d)}\}$$\left\{\mathbf{\vec w}^{(1)},\cdots,\mathbf{\vec w}^{(d)}\right\}$，其中 $d$$d$ 表示 hidden size 。

   根据卷积定理，频域中的乘法等效于时域中的循环卷积。这是两个具有相同周期的周期函数之间周期卷积（periodic convolution）的一种特殊情况。对于来自 item representation matrix ${\mathbf{F}}^l$$\mathbf F^l$ 的第 $t$$t$ 维特征 ${\left\{f_n^{(t)}\right\}}_{n=0}^{N-1}$$\left\{f_n^{(t)}\right\}_{n=0}^{N-1}$ 和滤波器 ${\left\{h_n^{(t)}\right\}}_{n=0}^{N-1}={\mathcal{F}}^{-1}\left(w^{(t)}\right)$$\left\{h_n^{(t)}\right\}_{n=0}^{N-1}=\mathcal F^{-1}\left(w^{(t)}\right)$，它们的循环卷积 ${\left\{y_n^{(t)}\right\}}_{n=0}^{N-1}$$\left\{y_n^{(t)}\right\}_{n=0}^{N-1}$ 定义为：

   $$y_n^{(t)}=\sum _{m=0}^{N-1}{h}_m^{(t)}\times f_{(n-m)\mathrm{mod}N}^{(t)}$$

   其中：mod 表示取模运算；$N$$N$ 是序列长度；$1\le t\le d$$1\le t\le d$ 表示第 $t$$t$ 维。

   假设序列 ${\left\{y_n^{(t)}\right\}}_{n=0}^{N-1}$$\left\{y_n^{(t)}\right\}_{n=0}^{N-1}$ 的 DFT 是 ${\left\{{\tilde{x}}_n^{(t)}\right\}}_{n=0}^{N-1}$$\left\{\tilde x_n^{(t)}\right\}_{n=0}^{N-1}$，我们有以下推导：

   $$\begin{array}{c}{\tilde{x}}_k^{(t)}=\sum _{n=0}^{N-1}\sum _{m=0}^{N-1}{h}_m^{(t)}{f}_{(n-m)\mathrm{\%}N}^{(t)}\exp (-\frac{2\pi i}{N}kn)\\ =\sum _{m=0}^{N-1}{h}_m^{(t)}\exp (-\frac{2\pi i}{N}km)\sum _{n=0}^{N-1}{f}_{(n-m)\mathrm{\%}N}^{(t)}\exp (-\frac{2\pi i}{N}k(n-m))\\ =w_k^{(t)}(\sum _{n=m}^{N-1}{f}_{n-m}^{(t)}\exp (-\frac{2\pi i}{N}k(n-m))+\sum _{n=0}^{m-1}{f}_{n-m+N}^{(t)}\exp (-\frac{2\pi i}{N}k(n-m)))\\ =w_k^{(t)}(\sum _{n=0}^{N-m-1}{f}_n^{(t)}\exp (-\frac{2\pi i}{N}kn)+\sum _{n=N-m}^{N-1}{f}_n^{(t)}\exp (-\frac{2\pi i}{N}kn))\\ =w_k^{(t)}\sum _{n=0}^{N-1}{f}_n^{(t)}\exp (-\frac{2\pi i}{N}kn)=w_k^{(t)}{x}_k^{(t)}\end{array}$$

   在等式右边，$x_k^{(t)}$$x_k^{(t)}$ 恰好是频域中 $\mathbf{X}$$\mathbf X$ 的第 $t$$t$ 维特征的第 $k$$k$ 个值，$w_k(t)$$w_k{(t)}$ 是第 $t$$t$ 个滤波器 ${\overrightarrow{\mathbf{w}}}^{(t)}$$\mathbf{\vec w}^{(t)}$ 的第 $k$$k$ 个权重。

3. 综上所述，我们证明了：

   $$f^{(t)}\ast h^{(t)}={\mathcal{F}}^{-1}({\overrightarrow{\mathbf{w}}}^{(t)}\odot {\overrightarrow{\mathbf{x}}}^{(t)})$$

   其中：$\ast$$*$ 和 $\odot$$\odot$ 分别表示循环卷积和逐元素乘法。

   因此，item representations ${\mathbf{X}}^l$$\mathbf X^l$ 的第 $t$$t$ 维特征与 $\mathbf{W}$$\mathbf W$ 中第 $t$$t$ 个滤波器 ${\overrightarrow{\mathbf{w}}}^{(t)}$$\mathbf{\vec w}^{(t)}$ 的乘法，等效于使用卷积核 ${\left\{h_n^{(t)}\right\}}_{n=0}^{N-1}$$\left\{h_n^{(t)}\right\}_{n=0}^{N-1}$ 对 ${\mathbf{F}}^l$$\mathbf F^l$ 的第 $t$$t$ 维特征进行循环卷积操作。与 RNN、CNN 和 Transformer 类似，所提出的 filter block 也能够捕获 sequential characteristics ，因为它本质上具有与循环卷积相同的效果。此外，与先前工作中的传统线性卷积相比，循环卷积在整个序列上具有更大的感受野，并且能够更好地捕获周期性模式。这一优点在推荐任务中特别有吸引力，因为用户行为往往表现出一定的周期性趋势。

1.3.3 讨论

1. 与基于 Transformer 的序列推荐器的比较：基于 Transformer 的模型，如 SASRec 和 BERT4Rec，通常堆叠 multi-head self-attention blocks 来学习 sequential representations。它依赖于复杂的 self-attention 结构来学习 item-to-item correlations 。相比之下，我们的 FMLP-Rec 方法直接去除了所有 self-attention structures ，整个方法仅基于 MLP 结构，并集成了额外的 filter layers 。这样的设计可以大大降低对序列数据建模的空间和时间复杂度。更重要的是，我们已经证明 learnable filter layer 等效于使用与 feature map 大小相同的卷积核进行循环卷积操作。因此，它可以拥有与自注意力机制相同的感受野，但大大减少了涉及的参数数量。此外，循环卷积能够捕获周期性特征（periodic characteristics ），这也是序列推荐的一个重要特征。

2. 时间复杂度和感受野分析：在本部分，我们从时间复杂度和感受野方面将我们的模型与代表性的序列推荐模型进行比较。我们选择基于 CNN 的 Caser 、以及基于 Transformer 的 SASRec 作为比较对象，因为它们代表了两种不同的神经架构。由于这些模型涉及不同的算法细节（例如 dropout 和 normalization ），直接比较可能不公平。相反，我们仅考虑序列长度 $n$$n$ 进行更通用的比较。模型复杂度和感受野的比较结果如 Table 2 所示。

   • 首先，Caser 在时域中执行卷积操作，因此其时间复杂度和感受野分别为 $O(kn)$$O(kn)$ 和 $k$$k$ ，然而，由于 Caser 依赖卷积核来捕获序列模式，通常需要更大的核大小来扩展感受野以获得更好的性能。

   • 此外，在基于 Transformer 的模型中，自注意力层需要计算每对 items 之间的相似度，其时间复杂度和感受野分别为 $O(n^2)$$O(n^2)$ 和 $n$$n$。

   • 相比之下，我们的 FMLP-Rec 由 FFT 和 IFFT 操作组成，时间成本为 $O(n\log n)$$O(n\log n)$；以及逐点前馈网络，时间成本为 $O(n)$$O(n)$。这意味着总时间复杂度为 $O(n\log n)$$O(n\log n)$。此外，由于我们的 filter layer 等效于对整个序列进行循环卷积，其感受野与Transformer 相同。因此，我们的 FMLP-Rec 可以实现更大的感受野，同时具有更低的复杂度。

   

1.4 实验

1. 数据集：我们在八个不同领域的数据集上进行实验，其统计信息总结在 Table 3 中。

   • Beauty, Sports, and Toys ：这三个数据集来自文献 《Image-Based Recommendations on Styles and Substitutes》 中的 Amazon 评论数据集。我们选择了三个子类别：Beauty, Sports and Outdoors, Toys and Games 。

   • Yelp：这是一个用于商业推荐的数据集。由于其规模非常大，我们仅使用 2019 年 1 月 1 日之后的交易记录。

   • Nowplaying：该数据集包含从 Twitter 收集的音乐收听事件，用户在 Twitter 上发布了他们当时正在收听的曲目。

   • RetailRocket：该数据集收集自一个个性化电子商务网站，包含六个月的用户浏览活动。

   • Tmall：来自 IJCAI-15 竞赛，包含用户在天猫在线购物平台上的购物日志。

   • Yoochoose：包含来自一家零售商的 sessions 集合，每个 session 封装了点击事件。

   注意，Beauty、Sports、Toys 和 Yelp 数据集中的 item sequences 是用户交易记录，而 Nowplaying、RetailRocket、Tmall 和 Yoochoose 数据集中的 item sequences 是 click sessions 。对于所有数据集，我们按用户或会话对交互记录进行分组，并按时间戳升序排序。遵循文献 《Parallel Recurrent Neural Network Architectures for Feature-rich Session-based Recommendations》、《Factorizing personalized Markov chains for next-basket recommendation》，我们过滤掉交互记录少于五条的不热门 items 和不活跃用户。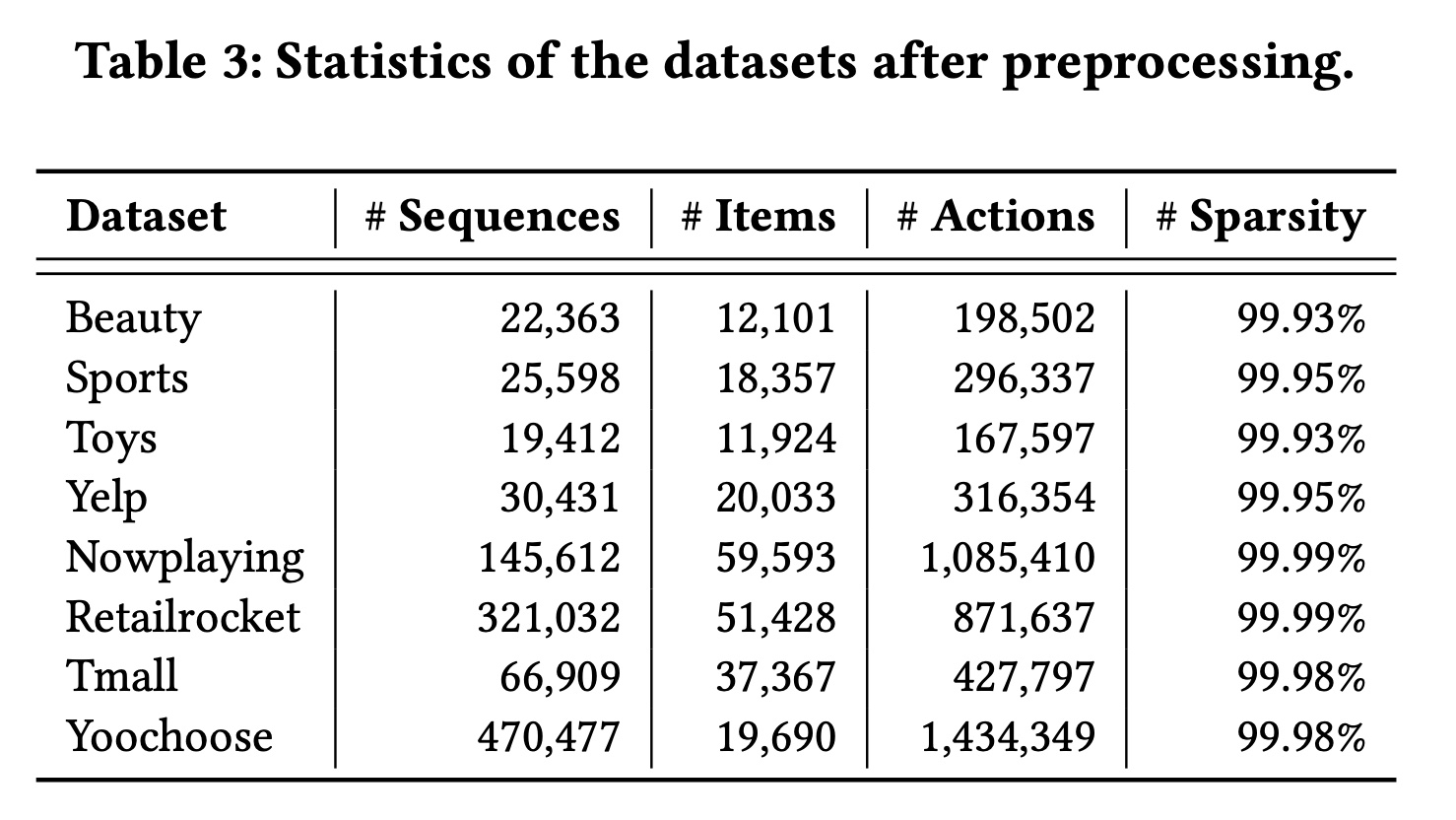

   

2. 评估指标：遵循文献 《Revisiting Alternative Experimental Settings for Evaluating Top-N Item Recommendation Algorithms》，我们采用 top-k Hit Ratio（HR@k）、top-k Normalized Discounted Cumulative Gain （NDCG@k）、以及 Mean Reciprocal Rank: MRR 进行评估，这些指标在相关工作中被广泛使用。由于 HR@1 等于 NDCG@1，我们报告 HR@{1, 5, 10}、NGCG@{5, 10} 和 MRR 的结果。遵循常见策略，我们将 ground-truth item 与 99 个随机采样的用户未交互过的 negative items 配对。我们根据 items 的排名计算所有指标，并报告平均得分。

   注意，我们还将 ground-truth item 与 all candidate items 进行排名，并在补充材料中报告完整排名结果。

3. 基线模型：我们将提出的方法与以下基线方法进行比较：

   • PopRec：根据交互次数衡量的流行度对 items 进行排名。

   • FM：使用因子分解模型来刻画变量之间的 pairwise interactions 。

   • AutoInt：利用多头自注意力神经网络学习 feature interactions。

   • GRU4Rec：应用 GRU 对 item sequences 进行建模。

   • Caser：一种基于 CNN 的方法，应用水平卷积和垂直卷积进行序列推荐。

   • HGN：采用 hierarchical gating networks 来捕获长期的和短期的用户兴趣。

   • RepeatNet：在 RNN 架构上添加 copy 机制，可以从用户历史中选择 items 。

   • CLEA：最近提出的方法，通过对比学习模型在 item-level 进行去噪。

   • SASRec：一种基于单向 Transformer 的序列推荐模型。

   • BERT4Rec：通过双向 Transformer 使用完形填空目标损失进行序列推荐。

   • SRGNN：将 session sequences 建模为图结构数据，并使用注意力网络。

   • GCSAN：利用图神经网络和自注意力机制进行 session-based 的推荐。

1.4.1 实验结果

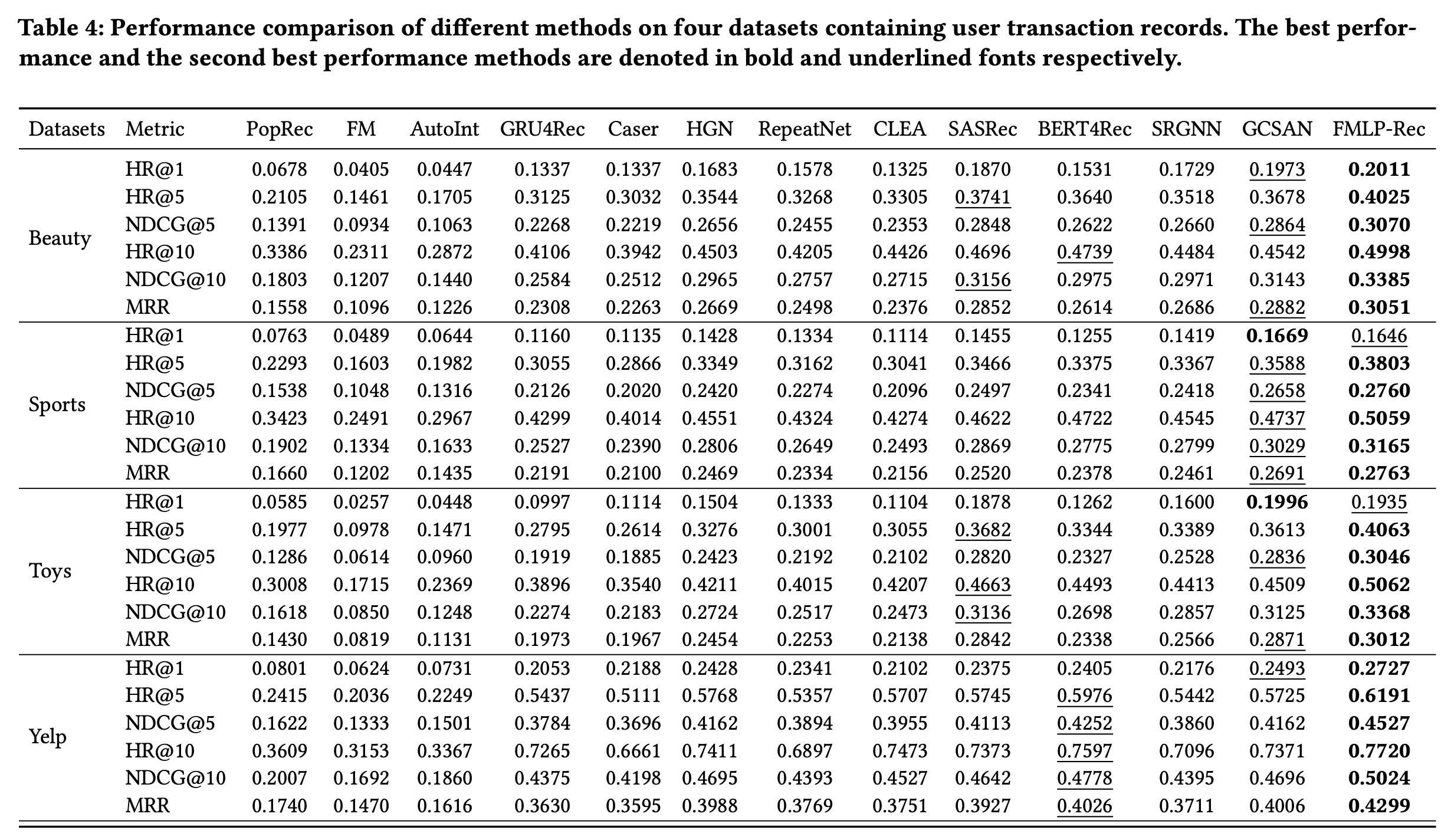
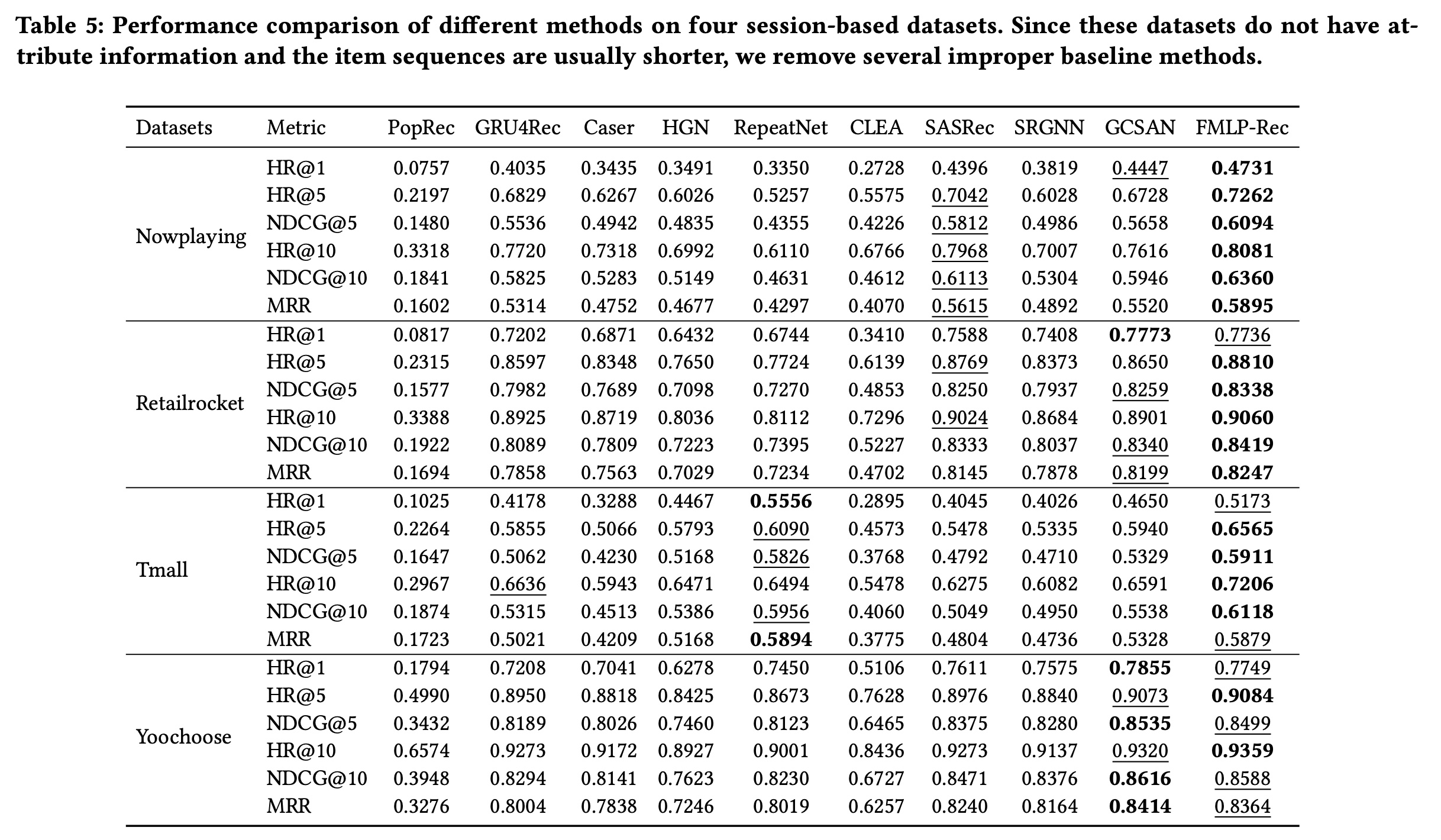
1. 不同方法在包含用户交易记录的数据集上的结果如 Table 4 所示，在基于会话的数据集上的结果如 Table 5 所示。基于这些结果，我们可以发现：

   • 首先，非序列推荐方法（即 PopRec、FM 和 AutoInt）的表现比序列推荐方法差，这表明序列模式在该任务中很重要。

   • 对于序列推荐方法，SASRec 和 BERT4Rec 利用基于 Transformer 的架构，大多比基于 RNN 的模型（即 GRU4Rec 和 RepeatNet）、基于 CNN 的模型（即 Caser）和基于门控的模型（即 HGN）表现更好。一个可能的原因是基于 Transformer 的模型具有更多参数，相应地具有更强的捕获 sequential characteristics 的能力。

   • 此外，CLEA 在部分数据集上实现了与 SASRec 和 BERT4Rec 相当的性能。由于 CLEA 采用了 item-level 降噪策略，这表明减轻噪声的影响有助于提高推荐性能。

   • 我们还可以看到，基于 GNN 的模型（即 SRGNN 和 GCSAN）也实现了与基于 Transformer 的模型相当的性能，这表明 GNN 在捕获用于准确推荐的有用特征方面也很有前景。

   • 最后，通过将我们的方法与所有基线进行比较，可以明显看出 FMLP-Rec 在大多数数据集上的表现始终优于它们，且优势明显。与这些基线不同，我们采用带有 learnable filters 的 all-MLP 架构对 item sequence 进行编码。learnable filters可以减轻噪声信息的影响，并且等效于循环卷积，能够以更大的感受野捕获 item sequences 中的 periodic characteristics 。all-MLP 架构大大减小了模型规模，导致更低的时间复杂度。因此，我们的 FMLP-Rec 是有效且高效的。这个结果也表明 all-MLP 架构对于序列推荐是有效的。

   

   

2. 完整排名结果（ground-truth item 与 all candidate items 进行排名）：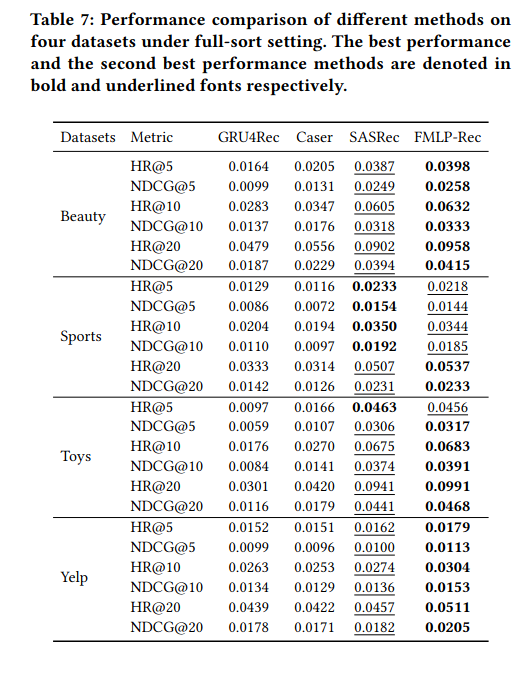

   

1.4.2 进一步分析

1. 消融研究：我们提出的 FMLP-Rec 包含 filter layers 、前馈网络和 Add & Norm 操作。为验证每个组件的有效性，我们在 Beauty 和 Sports 数据集上进行消融研究，分析每个部分的贡献。此外，为验证 learnable filters 是否比经典滤波算法更有用，我们还进行了变体研究，用高通滤波器、低通滤波器、以及带阻滤波器替换 learnable filters 。

   从 Table 6 的结果中，我们可以观察到：

   • 移除任何组件都会导致性能下降，尤其是 filter layer 。这表明 FMLP-Rec 中的所有组件都有助于提高推荐性能。

   • 此外，我们可以看到，我们的 FMLP-Rec 优于所有使用经典滤波算法的变体。原因是我们的 learnable filters 可以通过 SGD 自适应地学习过滤噪声信息，更有望更好地适应数据分布。

   实验部分缺乏训练时间的对比。

   另外，采用 LPF 已经能够获得比较好的效果，同时模型参数更少、计算量更少。但是，LPF 的阈值需要调优，因此需要多次训练才能得到一个好的阈值。整体代价并不低。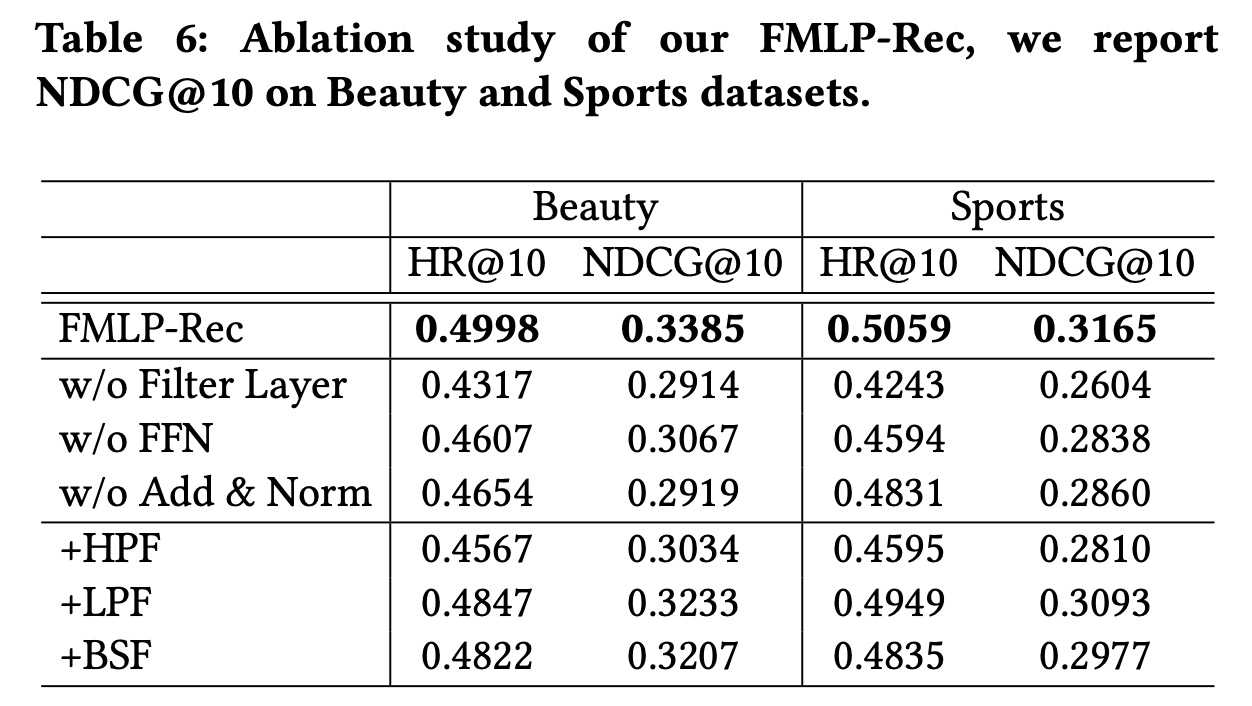

   

2. 将 Learnable Filters 应用于其他模型：FMLP-Rec 的关键贡献在于 learnable filters 。它是一个通用模块，可以应用于其他序列推荐模型。因此，在本部分中，我们检验我们的 learnable filters 是否能为其他模型带来性能提升。与实证分析章节中的操作类似，我们在 embedding layer 和 sequence encoder layer 之间添加 learnable filters ，并选择 RNN-based GRU4Rec 、CNN-based Caser 、Transformer-based SASRec 、以及 GNN-based GCSAN 作为基础模型。

   结果如 Figure 3 所示。我们还报告了 FMLP-Rec 的性能作为比较。

   • 首先，在集成了我们的 learnable filters 后，所有基线模型都实现了更好的性能。这表明 learnable filters 通常有助于减少其他模型中噪声信息的影响，即使对于不同的架构也是如此。

   • 其次，我们的 FMLP-Rec 仍然优于所有基线模型及其变体。这是因为我们的模型仅采用 MLP layers，参数较少，在序列推荐任务中更适合 learnable filters 。